作者：翟天保Steven
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处
摘要
锥形束计算机断层扫描（Cone Beam Computed Tomography, CBCT）凭借其结构紧凑、辐射剂量低、成像速度快等优势，在医学影像领域得到广泛应用。FDK算法作为CBCT图像重建的主流近似解析算法，通过投影数据预加权、滤波及反投影等核心步骤，实现了从二维投影数据到三维密度函数的高效重建。本文基于FDK算法的原始理论及后续发展研究，系统阐述其技术背景、核心技术原理与详细技术路线，明确各步骤的数学模型与实现逻辑，并通过流程图直观呈现重建全流程，为FDK算法的工程实现与应用提供技术参考。
上海艾普强粒子设备有限公司于上海嘉定瑞金医院部署的360旋转束治疗室，就是基于CBCT图像引导系统实现智能三维定位，配合治疗床完成病人精准治疗。
1 技术背景
在医学诊断与治疗领域，三维影像重建技术是获取人体内部结构信息的关键手段。早期CT成像多采用扇束扫描模式，需通过多层连续扫描拼接实现三维成像，存在辐射剂量高、成像效率低、机械结构复杂等不足。随着平板探测器技术的发展，CBCT系统应运而生，其采用锥形X射线束与二维平板探测器组合，单次旋转即可获取物体的完整二维投影数据，大幅简化了机械结构，降低了辐射剂量，同时提升了成像速度，广泛应用于口腔正畸、骨科导航、肿瘤放疗定位等场景。
从重建算法分类来看，CBCT重建算法主要分为解析算法与迭代算法。迭代算法虽重建精度较高，但存在计算复杂度高、重建耗时久、内存占用大等问题，难以满足临床实时成像需求。解析算法则通过数学解析推导实现重建，具有计算效率高、易于工程实现的优势，成为实际临床系统的主流选择。在解析算法中，FDK算法由Feldkamp、Davis和Kress于1984年提出，是二维扇束滤波反投影算法向三维锥形束场景的自然扩展，其数学形式简洁，在适度锥角条件下可获得良好的重建效果，克服了早期锥束重建算法对扫描轨迹的严格限制（如需球面扫描轨迹），显著降低了系统实现难度，至今仍是医学CBCT系统中应用最广泛的重建算法之一。
尽管FDK算法存在锥角增大时重建伪影加剧的固有缺陷，但后续学者基于该算法衍生出一系列改进算法（如G-FDK、T-FDK、HT-FDK等），有效拓展了其应用场景，提升了重建精度与适用范围，进一步巩固了其在医学CBCT重建领域的核心地位。
2 技术原理
2.1 核心几何模型
FDK算法基于圆轨道扫描几何模型，其核心几何关系如图1图2所示，图2中心为虚拟探测器。定义如下关键参数：
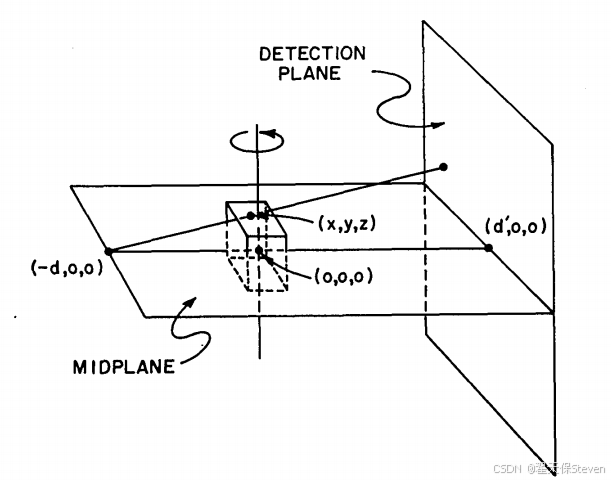
图1 几何关系示意图1
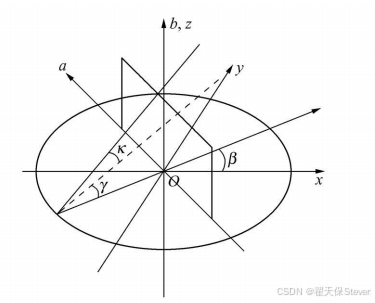
图2 几何关系示意图2
- X射线源S到旋转轴（Z轴）的距离为d（源到旋转轴距离SAD）；
- X射线源S到平板探测器平面的距离为D（源到探测器距离SID），满足D = d + d'（d'为旋转轴到探测器平面距离）；
- 投影角度β：X射线源与旋转轴的连线在X-Y平面内与X轴的夹角，范围为[0, 2π]；
- 探测器坐标(a, b)：虚拟平板探测器上像素的二维坐标，a为水平方向（平行于旋转轴所在平面），b为垂直方向（垂直于旋转轴所在平面）；
- 重建体素坐标(x, y, z)：待重建三维空间中点的坐标，旋转轴为Z轴，原点为旋转轴与中平面（垂直于Z轴且过旋转轴中点的平面）的交点。
在该几何模型中，X射线源与平板探测器围绕旋转轴同步旋转，每旋转一个角度β，探测器采集一幅二维投影图像，按空间几何比例关系映射至虚拟探测器p(β, a, b)，该投影数据本质上是X射线穿过物体后，在探测器上形成的强度分布，与物体内部的密度分布满足一定的积分关系。
2.2 核心算法推导
FDK算法的核心思想是将三维锥束重建问题分解为"加权-滤波-反投影"的分步处理过程，其本质是对二维扇束滤波反投影算法的三维扩展，通过引入锥角相关的加权因子，修正锥形束与扇束的几何差异。
首先，基于Radon变换理论，物体的二维投影数据p(l, θ)是密度函数f(r, φ)沿特定直线的线积分（扇束场景），其表达式为：
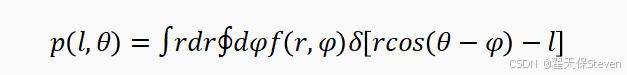
其中，l为原点到射线的垂直距离，θ为该垂直方向与X轴的夹角，δ为狄拉克函数。通过傅里叶变换与逆变换推导，可得到扇束滤波反投影重建公式。
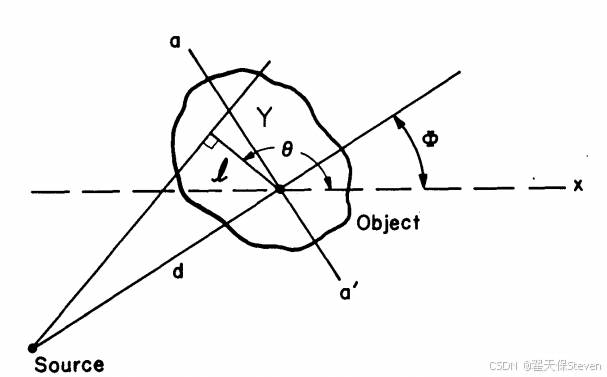
图3 扇束示意图
扩展到三维锥束场景时，FDK算法通过引入倾斜平面等效处理机制，将不同Z高度的投影数据视为倾斜扇束的投影，进而推导得到三维重建公式。其核心重建公式如下：
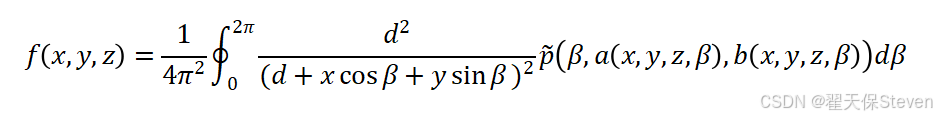
其中：
- f(x, y, z)为重建体素(x, y, z)的密度值；
为经过加权与滤波处理后的投影数据；
- a(x,y,z,β)、b(x,y,z,β)为重建体素(x, y, z)在角度β下对应的虚拟探测器坐标，由几何投影关系推导得出：
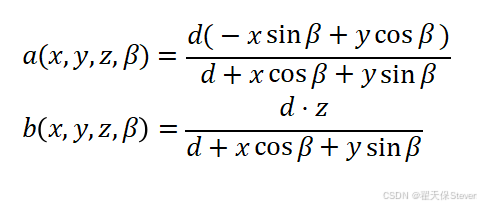
2.3 核心性质
FDK算法具有三个关键性质，保障了其在医学影像重建中的适用性：
- 中心平面精确性：对于垂直于旋转轴的中平面（z=0），FDK算法退化为标准的二维扇束滤波反投影算法，重建结果精确。离中平面越远，锥角越大，重建误差逐渐增大；
- Z方向一致性精确性：若物体密度在Z方向保持一致（即f(x,y,z)=f(x,y)），FDK算法可实现精确重建。此时投影数据经锥角相关加权后，等效于标准扇束投影数据；
- Z方向积分守恒性：重建结果沿Z方向的积分
3 技术路线
FDK算法的技术路线可分为五个核心步骤：X光图像采集、对数化处理、余弦加权、斜坡滤波、反投影重建。各步骤依次递进，形成从原始投影数据到三维重建图像的完整流程（为了方便读者理解，本文将以我实际使用的一组图像数据做展示）具体如下：
3.1 X光图像采集
采集装置由微焦点X射线源、单轴旋转台与二维平板探测器组成。被检测物体固定于旋转台上，X射线源与探测器同步围绕旋转轴旋转，旋转角度范围为[0, 2π]。在每个投影角度β下，探测器采集一幅二维投影图像，按空间几何比例关系映射至虚拟探测器，得到原始投影数据集，其中(β, a, b)分别对应投影角度、虚拟探测器水平坐标与垂直坐标。
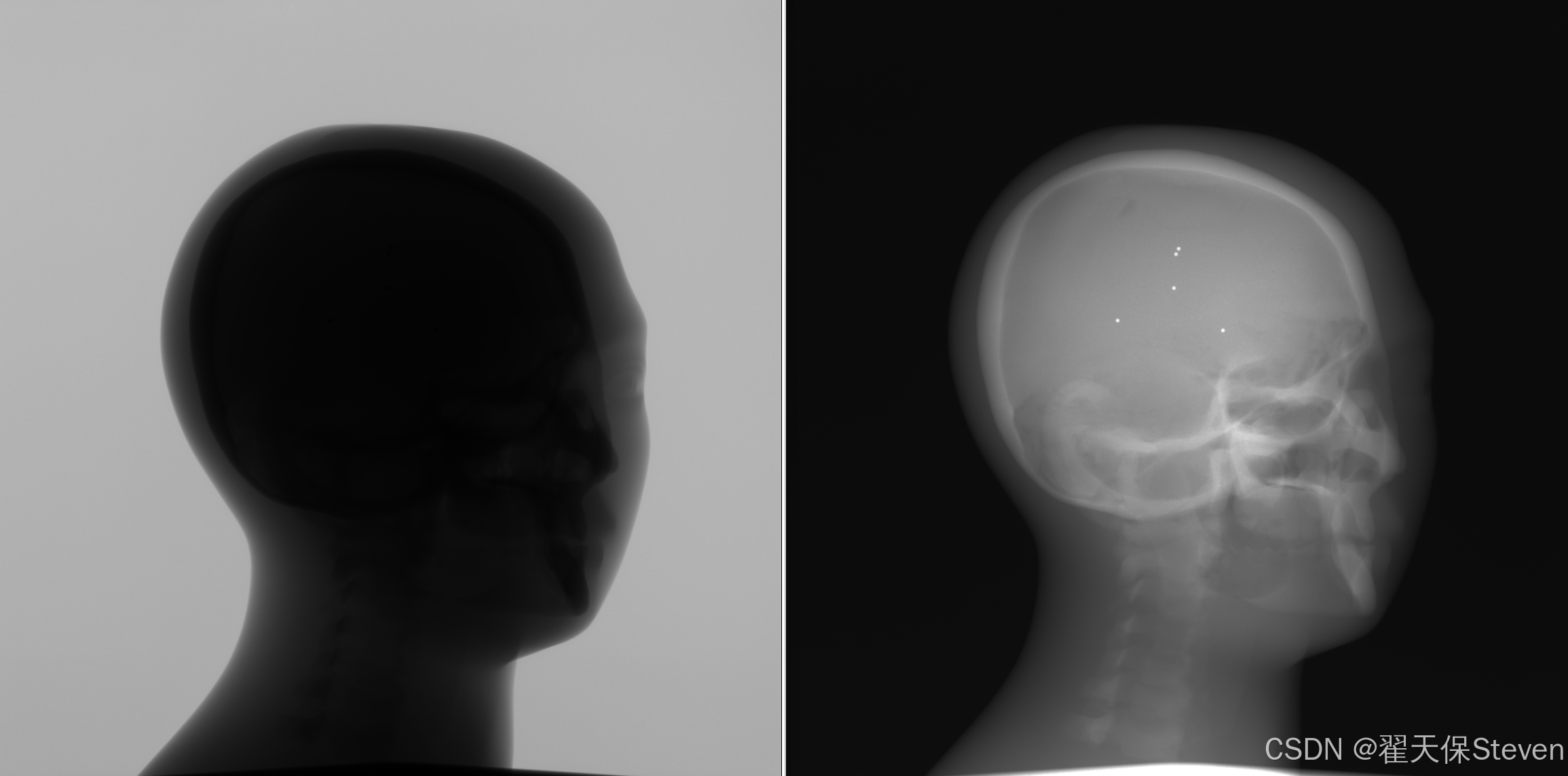
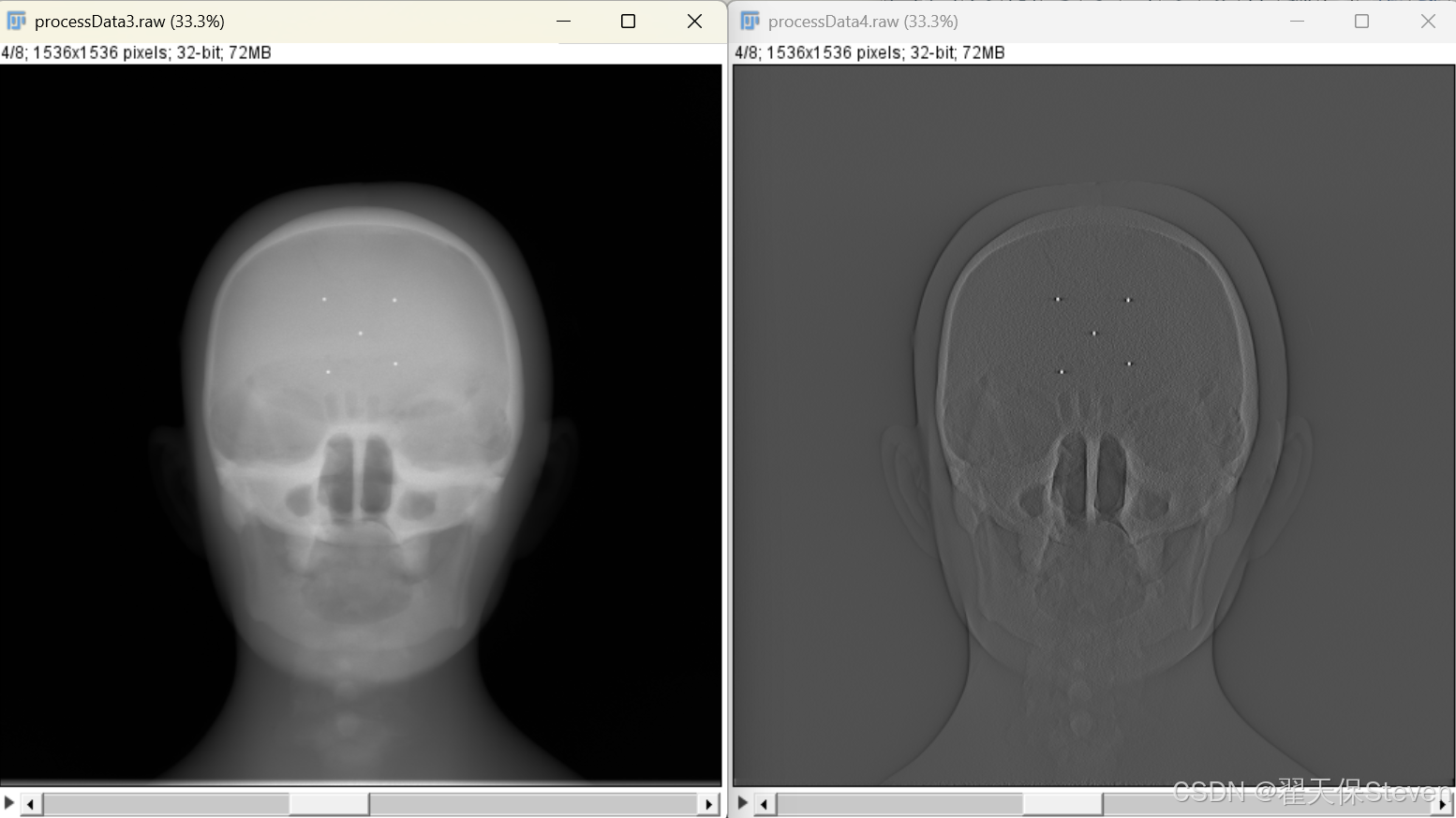
该步骤的核心是获取X射线穿过物体后的强度分布，其物理过程遵循朗伯-比尔（Beer-Lambert）定律：X射线强度随穿过物质的厚度与密度乘积呈指数衰减，为后续密度重建提供原始物理信号。采集图如下：
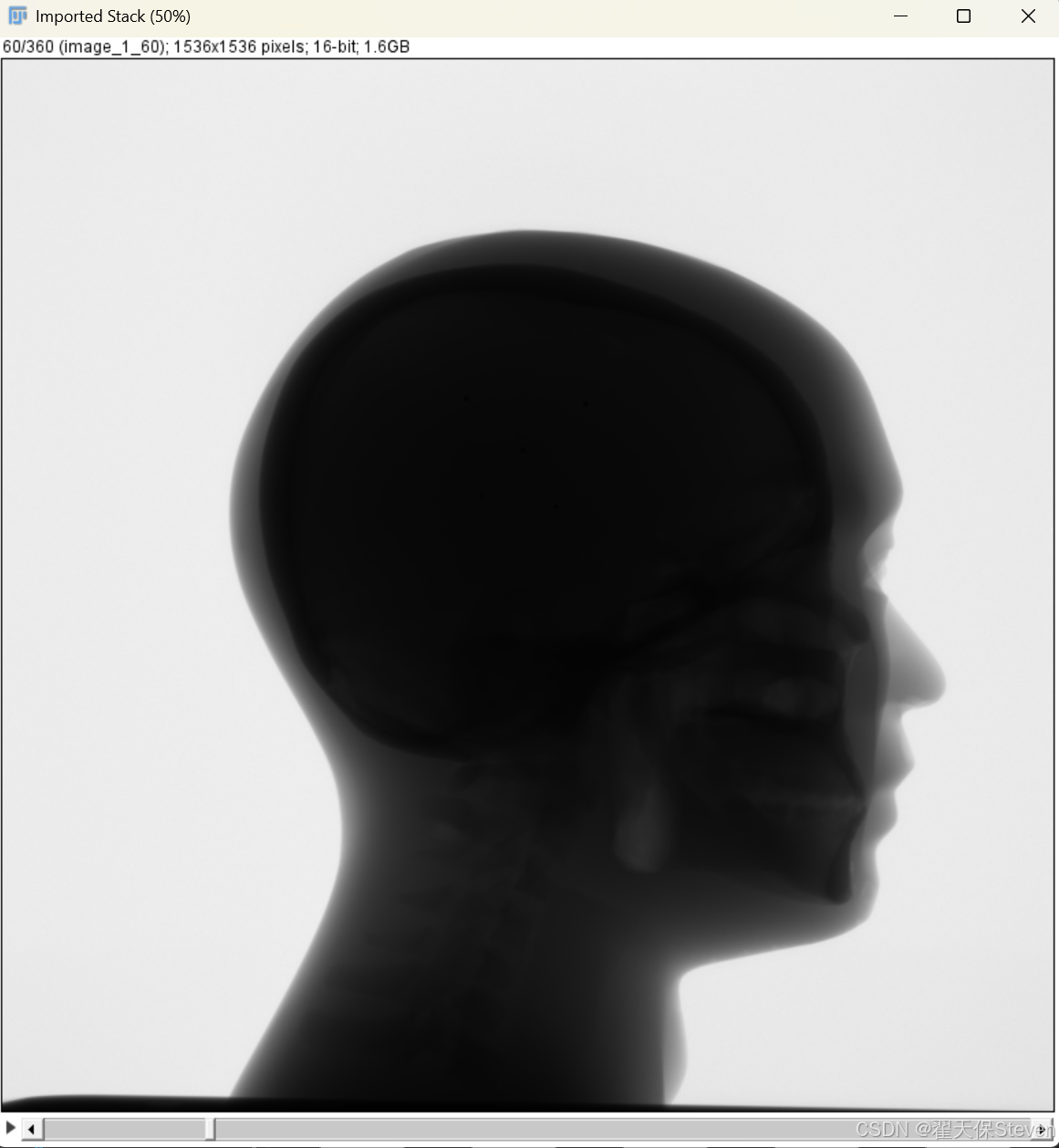
3.2 对数化处理
原始投影数据反映的是X射线穿过物体后的透射强度，需通过对数化处理转换为与物体密度相关的衰减系数投影数据。根据朗伯-比尔定律，X射线透射强度与物体衰减系数的关系为：
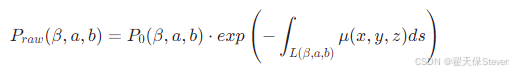
其中：
- ds为路径上的微小长度元。
对等式两边取自然对数，将指数关系转换为线性关系，得到衰减系数投影数据：
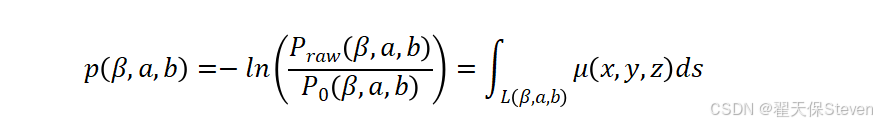
该步骤实现了从强度信号到衰减系数积分信号的转换，为后续重建物体密度分布奠定基础。
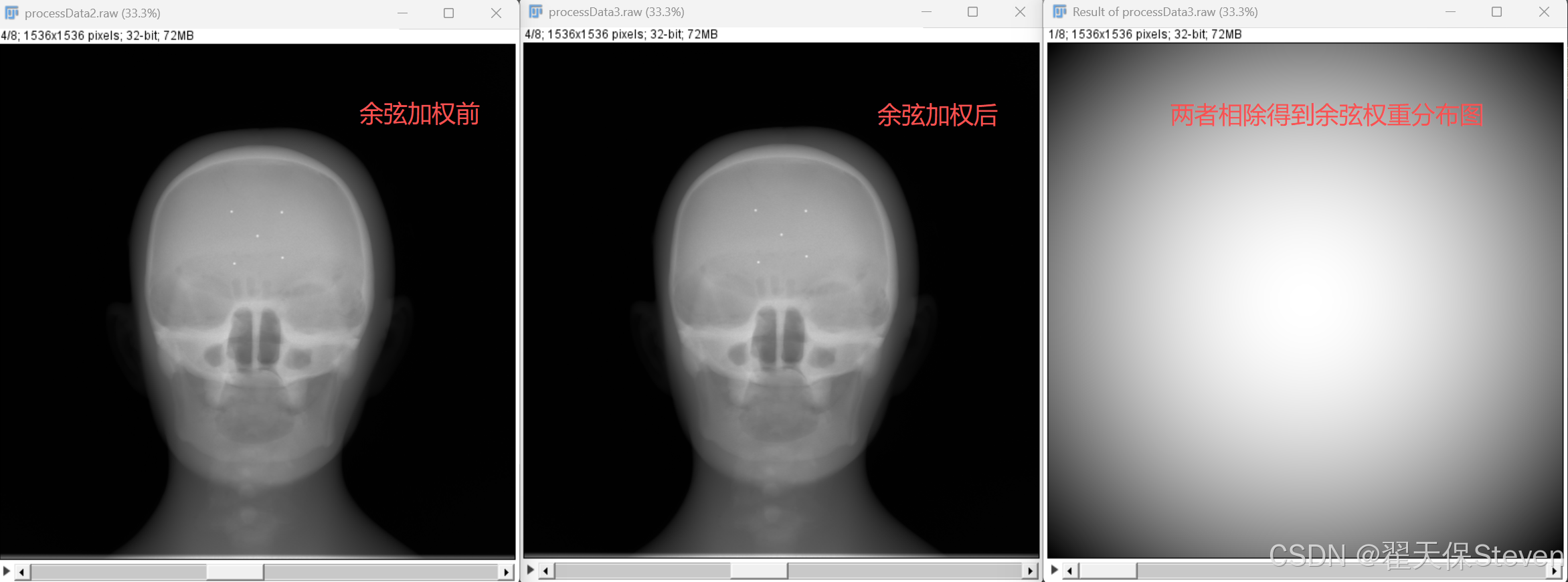
3.3 余弦加权
由于CBCT采用锥形束扫描，不同探测器位置的X射线传播路径长度与角度存在差异，导致投影数据存在几何衰减效应。为修正该效应，需对对数化后的投影数据进行余弦加权处理，本质是对不同角度的射线贡献进行均衡化。
加权因子的设计基于扫描几何关系，考虑扇角γ与锥角κ的综合影响，其表达式为：
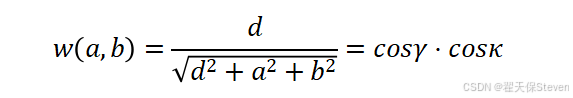
其中，d为源到旋转轴距离，a、b为探测器坐标，γ为扇角（X射线与旋转轴所在平面的夹角），κ为锥角（X射线与中平面的夹角）。
加权后的投影数据为：
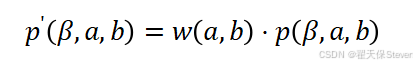
该步骤有效修正了锥形束几何带来的投影强度不均问题，使加权后的投影数据更接近理想扇束投影数据特性。
3.4 斜坡滤波
投影数据经过加权后，仍包含大量低频噪声与模糊信息，需通过滤波处理增强边缘细节，提取与物体密度突变相关的高频信息。FDK算法采用斜坡（Ramp）滤波函数，其核心是在频域对投影数据进行加权，放大高频成分。
斜坡滤波函数的频域表达式为：
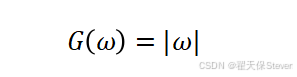
其中ω为频率变量。由于计算机处理的是离散数据，实际实现中需将频域滤波转换为空域卷积运算，滤波后的投影数据为：
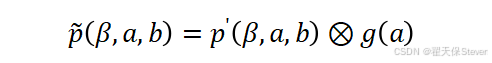
其中表示卷积运算，g(a)为斜坡滤波函数的空域形式。为避免滤波过程中产生的高频噪声放大，实际应用中常将斜坡滤波与窗函数（如Shepp-Logan窗）结合，平衡边缘增强与噪声抑制效果。
滤波过程的核心作用是补偿投影数据在采集过程中的"积分模糊"，还原物体密度的突变边界，为后续精确反投影提供清晰的投影信息。
3.5 反投影重建
反投影是将经过加权与滤波处理的投影数据，沿X射线传播的反方向映射到三维重建空间，累加形成物体的三维密度分布。其核心逻辑是：每个重建体素的密度值由所有穿过该体素的X射线对应的滤波后投影数据加权累加得到。
根据FDK算法的核心重建公式，离散化后的反投影计算式为：
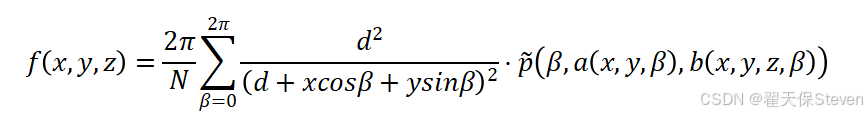
其中N为投影角度总数，为角度间隔的等效权重，
为反投影加权因子，用于修正X射线对不同位置重建体素的贡献权重。积分公式里的归一化系数
离散化时被省略，影响不大，因为重建完成后还要进行HU矫正。
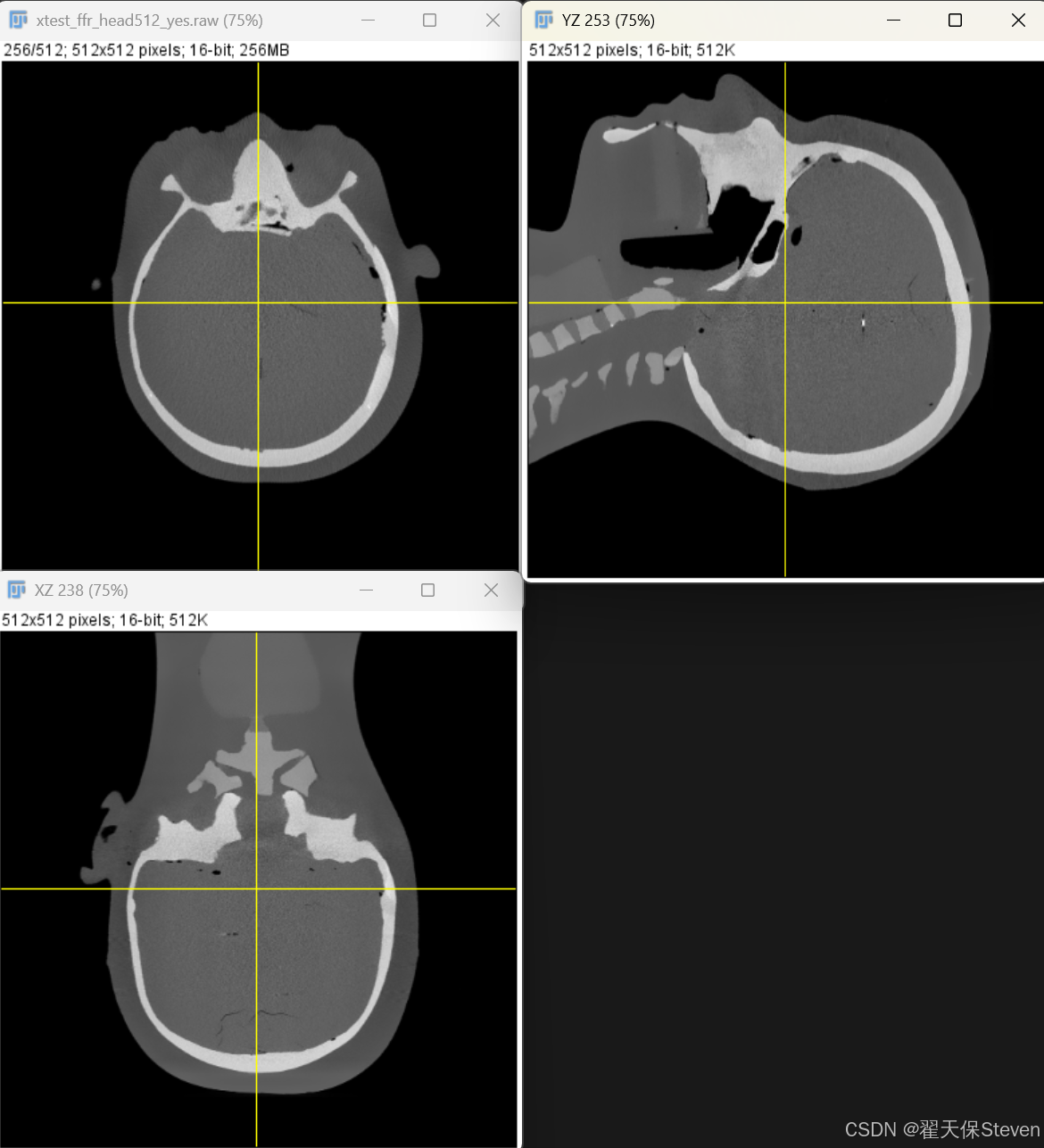
反投影过程中，需通过双线性插值计算重建体素在探测器上的对应坐标(a(x,y,β), b(x,y,z,β))处的滤波后投影数据，确保投影信息向三维空间的精确映射。重建后图像三视图如下所示（坐标系为Dicom-HFS体位）。
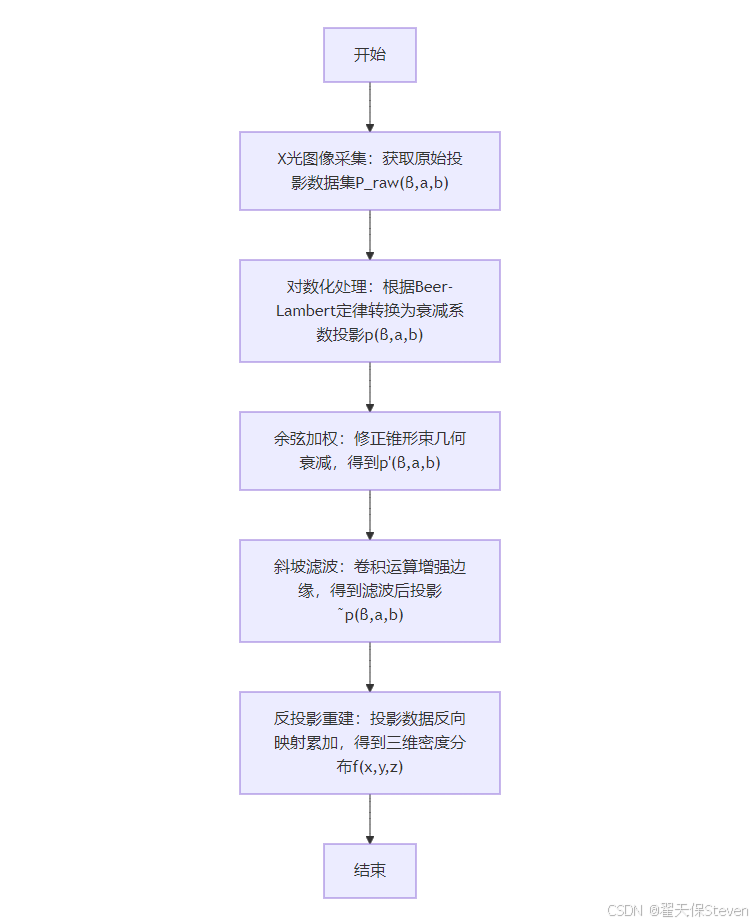
3.6 技术路线流程图
FDK算法完整技术路线的流程如下：
4 总结
FDK算法作为CBCT图像重建的经典近似解析算法，以其数学简洁性、高效性和良好的工程可实现性，成为医学影像领域的主流重建方案。其核心优势在于通过"加权-滤波-反投影"的分步处理，在适度锥角条件下实现了三维重建的精度与效率平衡，满足临床实时成像需求。本文阐述的技术路线清晰呈现了从原始X光图像采集到最终三维重建的全流程，明确了各步骤的数学模型与物理意义，其中对数化处理实现了强度信号到衰减系数的转换，余弦加权修正了锥形束几何偏差，斜坡滤波增强了边缘细节，反投影完成了二维信息到三维空间的映射。
尽管FDK算法存在锥角增大时轴向模糊与伪影加剧的缺陷，但后续衍生的G-FDK（任意轨道扩展）、T-FDK（锥向伪影抑制）、HT-FDK（重建体积扩大）等算法有效弥补了其不足。未来，结合GPU并行计算技术（如CUDA）可进一步提升FDK算法的重建速度，推动其在高精度、实时性要求更高的医学场景（如术中导航）中的应用。
目前我自研的重建算法基于CUDA实现，针对1536*1536*360二维X光图像序列重建512*512*512的场景，在引入了各类伪影矫正技术后，可以做到单帧15ms左右（非工作站，笔记本4060显卡），性能十分优越，欢迎技术控交流。
参考文献
1\] Feldkamp L A, Davis L C, Kress J W. Practical cone-beam algorithm\[J\]. J. Opt. Soc. Am. A, 1984, 1(6): 612-619. \[2\] 张剑, 陈志强. 三维锥形束CT成像FDK重建算法发展综述\[J\]. 中国体视学与图像分析, 2005, 10(2): 116-121. \[3\] 徐月晋, 陈梓嘉, 骆毅斌, 等. 锥束CT的改进FDK算法及加速实现\[J\]. 核电子学与探测技术, 2015, 35(11): 1124-1127.