大学院-筆記試験練習:线性代数和数据结构(8)
- 1-前言
- 2-线性代数-题目
- 3-线性代数-参考答案
- 4-数据结构-题目
- 5-数据结构-参考答案
- [一、【第 1 问】哈希法(翻译 + 解释)](#一、【第 1 问】哈希法(翻译 + 解释))
-
- 原题翻译
- 这一问到底在考什么?(非常重要)
-
- [🔑 核心对比](#🔑 核心对比)
- 标准结论(直接给答案)
- [✅ 第 1 问填空答案](#✅ 第 1 问填空答案)
- [二、【第 2 问】C 语言 + 哈希表(翻译 + 解释)](#二、【第 2 问】C 语言 + 哈希表(翻译 + 解释))
- 三、整题一句话总结(非常重要)
- 6-总结
1-前言
为了升到自己目标的大学院,所作的努力和学习,这里是线性代数和数据结构部分。
2-线性代数-题目

3-线性代数-参考答案



4-数据结构-题目


5-数据结构-参考答案
一、【第 1 问】哈希法(翻译 + 解释)

原题翻译
(1)
"什么是哈希值的冲突?请简要说明。"
👉 翻译:
不同的输入数据,通过哈希函数计算后,得到了相同的哈希值 ,这种情况称为哈希冲突。
(2)
在内部哈希法(开放地址法)中,考虑以下两种哈希函数序列((k=0,1,2,\dots)):
f_k(x) = (h_1(x) + k) \\bmod M
g_k(x) = (h_1(x) + k h_2(x)) \\bmod M
其中:
- (M):足够大的素数
- (a \bmod b):(a) 除以 (b) 的余数
h_1(x) = x \\bmod M
h_2(x) = 1 + (x \\bmod (M-1))
接下来这段是整题的核心
设 (N) 是远大于 (M) 的整数,从 (N) 未满的正整数中均匀随机选取 (x,y)。
-
当
f_0(x)=f_0(y)
时,
f_1(x)=f_1(y)
的概率记为 §
-
当
g_0(x)=g_0(y)
时,
g_1(x)=g_1(y)
的概率记为 (q)
要求:填空 A--D
这一问到底在考什么?(非常重要)
不是让你算复杂概率,而是在考你是否理解:
🔑 核心对比
| 方法 | 本质 |
|---|---|
| (f_k) | 线性探查(一步一步 +1) |
| (g_k) | 双重哈希(跳步长度与数据有关) |
👉 如果第一次冲突了:
- 线性探查:后面还容易继续冲突
- 双重哈希:第二次冲突的概率更低
标准结论(直接给答案)
-
若 (f_0(x)=f_0(y)),那么
f_1(x)=f_1(y) \\text{ 一定成立}
👉 所以
\\boxed{p = 1}
-
双重哈希中,
g_1(x)=g_1(y)
不一定成立,概率更小
✅ 第 1 问填空答案
| 空 | 答案 | 含义 |
|---|---|---|
| A | 1 | 线性探查下必然再次冲突 |
| B | 大きい | p 比 q 大 |
| C | (g_k(x)) | 更优(双重哈希) |
| D | (f_k(x)) | 较差(线性探查) |
📌 整句话的含义是:
因为线性探查在发生一次冲突后,后续仍然高概率冲突,而双重哈希能有效分散冲突,所以在内部哈希法中,使用 (g_k(x)) 比使用 (f_k(x)) 期望冲突次数更少。
二、【第 2 问】C 语言 + 哈希表(翻译 + 解释)
原题在说什么(翻译)
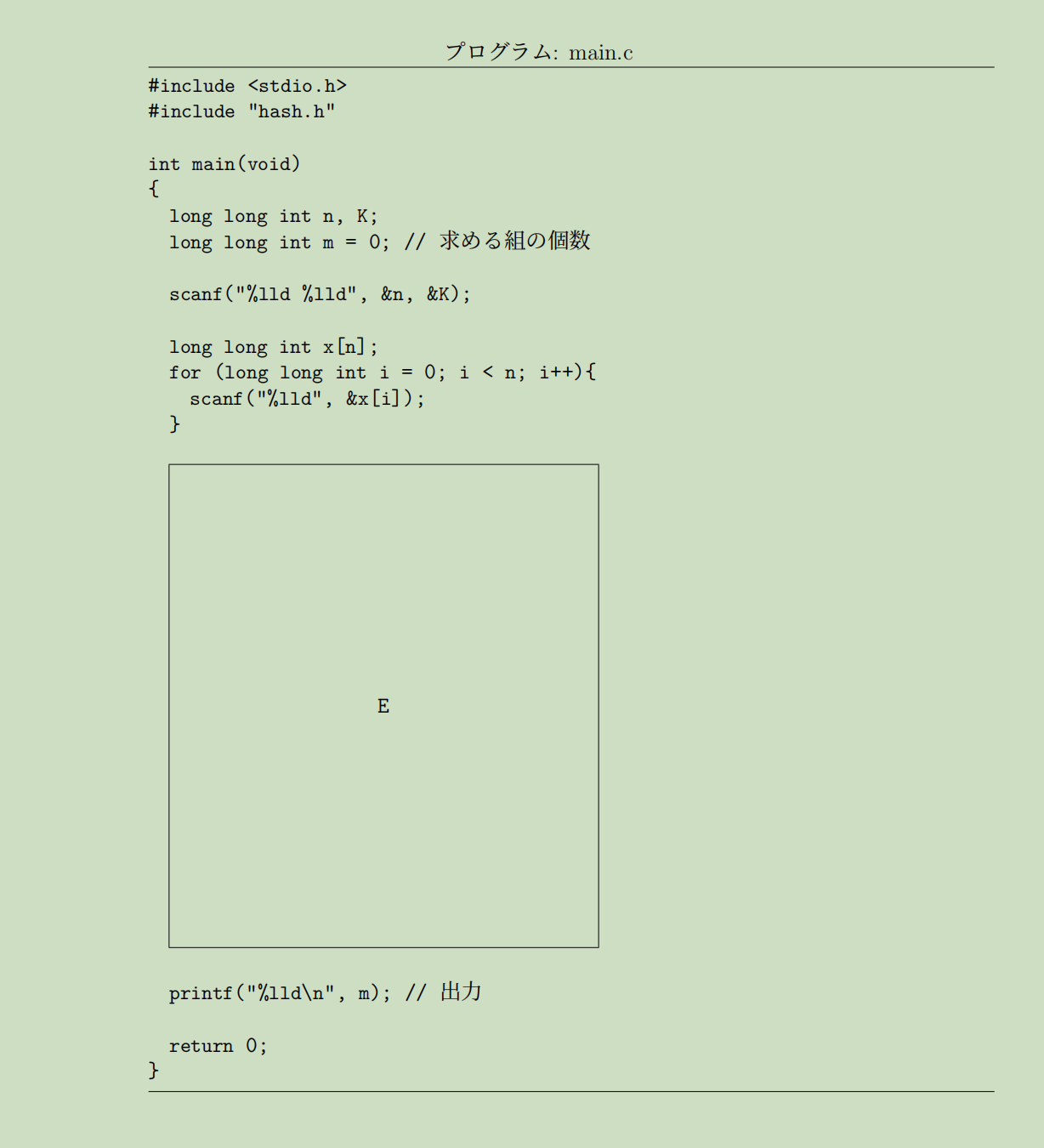
给定程序 main.c(C99),
它使用 hash.h 中的函数来管理一个正整数集合:
c
void initT(); // 初始化哈希表
void insertT(v); // 插入 v,失败则结束程序
int searchT(v); // 若存在返回 1,否则 0并且:
insertT和searchT的时间复杂度都是 O(1)
输入格式
- 输入两个整数
n, K - 输入
n个互不相同的正整数x1, x2, ..., xn
输出要求
输出满足:
1 \\le i \< j \\le n,\\quad x_i + x_j = K
的组合对数 (m)。
这一问在考什么?
👉 经典算法题:Two Sum(两数之和)
但重点不是算法竞赛,而是:
- 是否想到用 哈希表
- 是否能做到 O(n),而不是 (O(n^2))
- 是否会避免重复计数
正确思路(考试版)
思路一句话
先把所有数放进哈希表,再对每个 (x_i),检查 (K-x_i) 是否存在。
✅ 标准答案(E 中应写的代码)
c
// 初始化哈希表
initT();
// 插入所有元素
for (long long int i = 0; i < n; i++) {
insertT(x[i]);
}
// 统计满足 xi + xj = K 的对数
for (long long int i = 0; i < n; i++) {
long long int y = K - x[i];
if (y <= 0) continue; // 题目保证都是正整数
if (y == x[i]) continue; // 排除 i = j
if (searchT(y)) {
m++;
}
}
// 每一对被数了两次
m /= 2;时间复杂度
- 插入:(O(n))
- 查询:(O(n))
- 总体:
\\boxed{O(n)}
👉 这正是题目要求的"尽量高效"
三、整题一句话总结(非常重要)
这道题在考:
❗ 你是否理解哈希,而不是只会写哈希
具体包括:
- 什么是冲突
- 为什么双重哈希更好
- 如何把哈希用于实际算法
- 如何用 C 写出工程级代码
6-总结
训练成长。!!