题目
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
数据范围
树中节点数目在范围 [1, 104] 内
-100 <= Node.val <= 100
测试用例
示例1
java
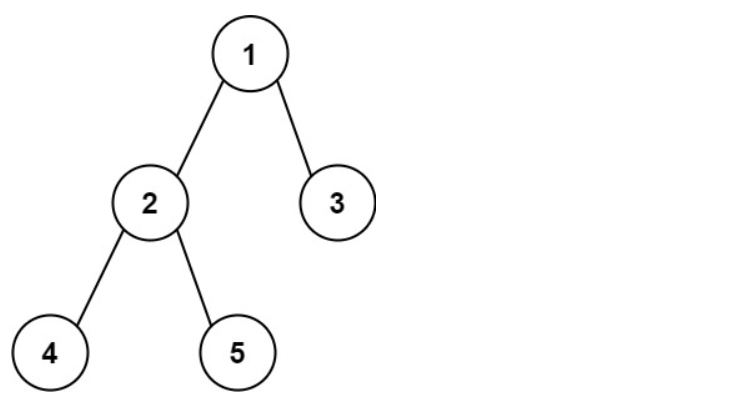
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。示例2
java
输入:root = [1,2]
输出:1题解1(递归 时间On 空间Oh)
java
class Solution {
int ans;
public int diameterOfBinaryTree(TreeNode root) {
ans = 1;
depth(root);
return ans - 1;
}
public int depth(TreeNode node) {
if (node == null) {
return 0; // 访问到空节点了,返回0
}
int L = depth(node.left); // 左儿子为根的子树的深度
int R = depth(node.right); // 右儿子为根的子树的深度
ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans
return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
}
}题解2(迭代 时空On)
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// 迭代法求二叉树直径
public int diameterOfBinaryTree(TreeNode root) {
// 边界情况:空树直径为0
if(root == null)
return 0;
// res记录当前找到的最大直径(节点数)
int res = 0;
// 栈用于后序遍历二叉树
Stack<TreeNode> stack = new Stack<>();
// map存储每个节点的高度(子树的最大深度+1)
Map<TreeNode, Integer> map = new HashMap<>();
// 根节点入栈
stack.push(root);
// 开始后序遍历
while(!stack.isEmpty()){
// 查看栈顶元素但不弹出
TreeNode t = stack.peek();
// 判断当前节点是否可以处理(后序遍历条件):
// 1. 左子树为空或已处理完(在map中)
// 2. 右子树为空或已处理完
if((t.left == null || map.containsKey(t.left)) &&
(t.right == null || map.containsKey(t.right))) {
// 弹出栈顶节点(当前节点)
stack.pop();
// 获取左右子树的高度,空节点高度为0
int l = map.getOrDefault(t.left, 0);
int r = map.getOrDefault(t.right, 0);
// 计算当前节点的直径:
// 直径 = 左子树高度 + 右子树高度 + 1(当前节点)
// 更新全局最大直径
res = Math.max(res, l + r + 1);
// 计算当前节点的高度:
// 高度 = max(左子树高度, 右子树高度) + 1
// 存入map供父节点使用
map.put(t, Math.max(l, r) + 1);
} else {
// 当前节点还不能处理,需要先处理子节点
// 注意:先判断左子树,然后右子树
// 因为栈是LIFO,所以实际执行顺序是:右子树先入栈,左子树后入栈
// 这样保证左子树先被处理(后序遍历:左→右→根)
if(t.left != null && !map.containsKey(t.left)){
stack.push(t.left);
}
if(t.right != null && !map.containsKey(t.right)){
stack.push(t.right);
}
}
}
// 返回直径长度(边数 = 节点数 - 1)
return res - 1;
}
}题解3(Morris 时间On 空间O1)
java
class Solution {
public int diameterOfBinaryTree(TreeNode root) {
// 边界情况:空树直径为0
if (root == null) return 0;
// 记录全局最大直径
int maxDiameter = 0;
// 当前遍历的节点,使用Morris遍历
TreeNode curr = root;
// Morris遍历二叉树(中序遍历的变种)
while (curr != null) {
if (curr.left == null) {
// 情况1:当前节点没有左子树
// 直接移动到右子树
curr = curr.right;
} else {
// 情况2:当前节点有左子树
// 找到当前节点在中序遍历下的前驱节点
// (即左子树中最右边的节点)
TreeNode predecessor = curr.left;
int steps = 1; // 记录左子树的高度(边数)
// 寻找前驱节点:一直往右走,直到:
// 1. 遇到空(找到最右节点)
// 2. 遇到当前节点(已经建立过线索)
while (predecessor.right != null && predecessor.right != curr) {
predecessor = predecessor.right;
steps++; // 每往右一步,高度加1
}
if (predecessor.right == null) {
// 第一次到达这个节点,建立线索
// 将前驱节点的右指针指向当前节点
// 这样在遍历完左子树后能回到当前节点
predecessor.right = curr;
// 移动到左子树继续遍历
curr = curr.left;
} else {
// 第二次到达这个节点(通过线索回来的)
// 说明左子树已经遍历完成
// 断开之前建立的线索,恢复树的原始结构
predecessor.right = null;
// 计算当前节点的直径:
// 需要计算左子树和右子树的高度
// 计算左子树的高度
// 注意:这里的左子树已经部分遍历过,但getHeight会重新计算
int leftHeight = getHeight(curr.left);
// 计算右子树的高度
int rightHeight = getHeight(curr.right);
// 更新全局最大直径
// 直径 = 左子树高度 + 右子树高度
maxDiameter = Math.max(maxDiameter, leftHeight + rightHeight);
// 移动到右子树继续遍历
curr = curr.right;
}
}
}
// 由于Morris遍历的特性,根节点在遍历过程中可能没有计算直径
// 所以需要额外计算根节点的直径
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
maxDiameter = Math.max(maxDiameter, leftHeight + rightHeight);
return maxDiameter;
}
// 辅助方法:递归计算二叉树的高度
// 高度定义:从节点到最远叶子节点的边数
// 空节点高度为0,叶子节点高度为0
private int getHeight(TreeNode node) {
if (node == null) return ;
// 节点高度 = 1 + max(左子树高度, 右子树高度)
return 1 + Math.max(getHeight(node.left), getHeight(node.right));
}
}思路
这道题求二叉树的直径,其实最简单最方便的方法就是递归,官解的答案也是递归,大家根据代码理解一下这道题的递归逻辑即可。但评论中有人说某大厂考到了迭代,那么博主这里写了两种迭代方法,一种是用hashmap,空间复杂度为On,是比较常见且好理解的方法。第二种是morris遍历,在遍历的基础上,在会遍历第二次的点出进行一个左右子树高度的计算,然后求值。整体来说都不难,morris也只是一个模板,记住就行了,大家多练多背多看