一、控制系统的状态空间表达式
1、状态空间表达式与传递函数的区别
线性定常系统的传递函数是指在初始状态为零的条件下,系统输出变量的拉氏变换与输入变量的拉氏变换之比
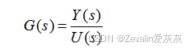
在经典控制理论中主要通过传递函数描述一个动态系统(的输入和输出之间的关系),它是控制系统的一个外部描述,并不关心系统的内部结构
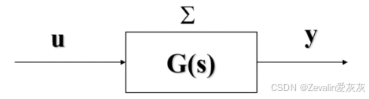
某些情况下,无论怎么改变系统的输入,都达不到所期望的输出,这时仅通过传递函数无法分析发生这种情况的原因
现代控制理论所要建立的控制系统的数学模型是系统的状态空间表达式,状态空间表达式不仅关心系统输入和输出的关系,更关心系统内部的结构,它通过引入反映系统内部状态变化的状态变量,构建出系统输入和输出之间的桥梁
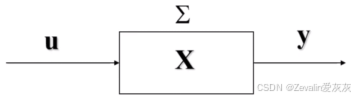
2、状态空间变量与状态向量
(1)足以完全表征系统运动状态的最少个数的一组变量,称为状态变量。

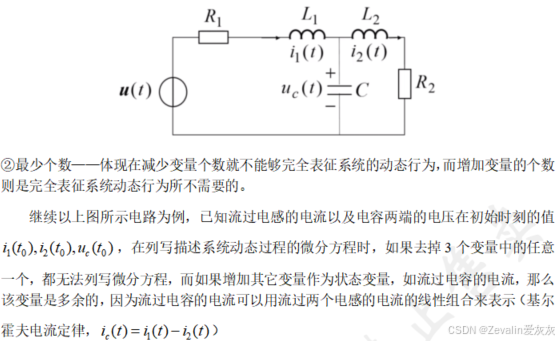
(2)关于状态变量的几点说明:
①状态变量是相互独立的,从数学的层面看是线性无关的,也即其中任何一个变量都不能用其它变量的线性组合来表示。
②对于一个实际的物理系统,状态变量的个数应大于等于系统中独立储能元件的个数,在实际分析中,需考虑对实际物理系统描述的精细程度要求。
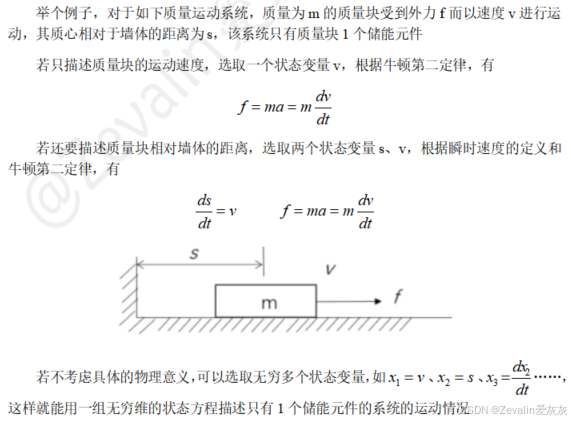
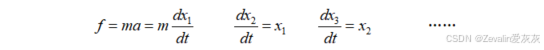
③对同一个动态系统,在内涵精度描述相同的情况下,状态变量的选取不是唯一的,但状态变量的个数是唯一确定的,不能多、也不能少。
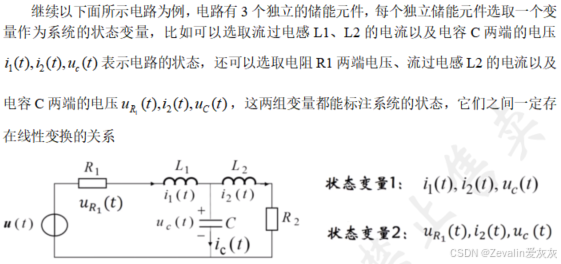
(3)由系统状态变量构成的向量,称为系统的状态向量。

3、状态空间表达式
(1)状态空间的概念:


(2)状态方程的概念:
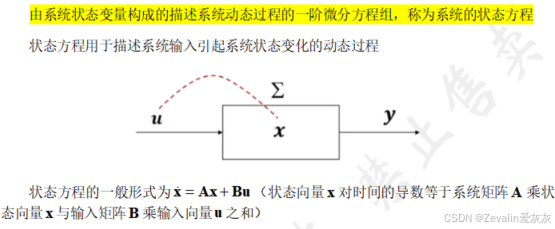
(3)输出方程的概念:
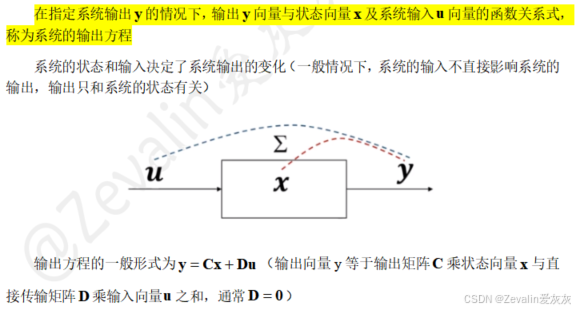
(4)状态空间表达式的概念:


(5)关于状态空间表达式的几点说明:
①状态空间表达式可以用系统方框图描述。
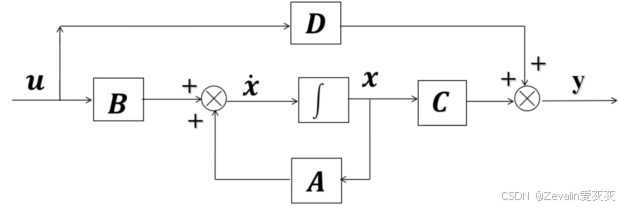
②输入引起系统状态的变化,而状态和输入则决定了输出的变化。
③状态空间表达式的方框图只含有比例、积分器(不是积分环节)、加法三类基本环节。
④在输出方程中,若无特殊声明,均不考虑输入向量的直接传输,即直接传输矩阵为零矩阵。
二、状态空间表达式的建立
1、根据系统的方框图列写状态空间表达式(方框图法)
(1)方框图法的基本思想:

(2)方框图法的基本步骤:
①对复杂的系统方框图进行变换,将包含高级环节的系统方框图变换为只包含比例、积分和加法环节的方框图。
②选取状态变量,将每一个积分器的输出选作一个状态变量。
③根据方框图各环节的关联关系,列写状态空间表达式。
(3)举例:
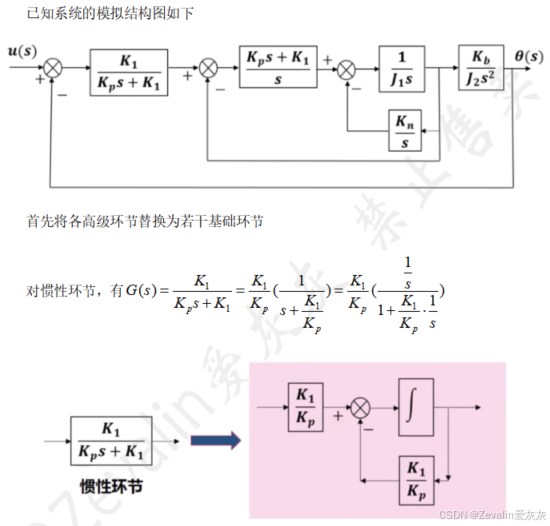
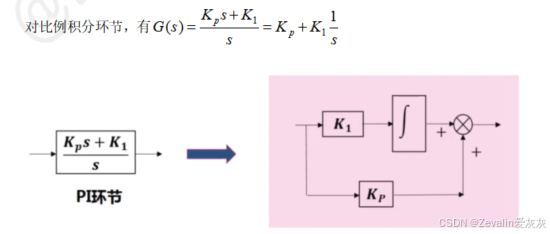
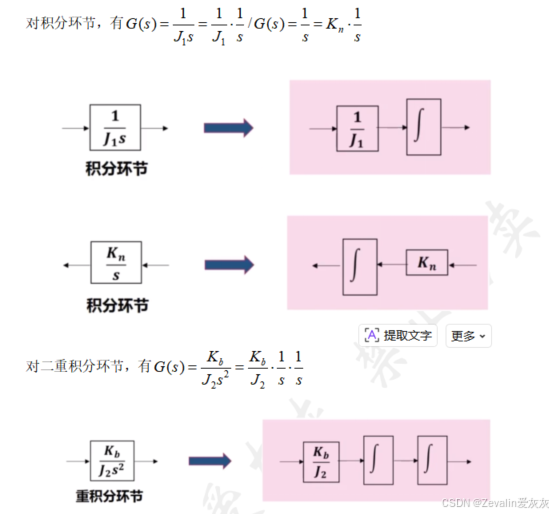
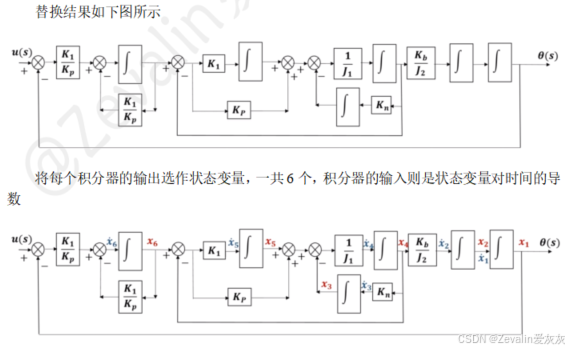

2、从系统的基本原理推导状态空间表达式(机理法)
(1)多数系统方框图是依据系统所遵循的基本机理推导而得,比如建立电力系统的状态空间表达式,则需要有电力系统分析的基础知识。
(2)从系统的机理出发建立状态空间表达式:
①对于实际物理系统,状态变量的个数通常等于系统中独立储能元件的个数,因此在列写状态方程时通常可对每一个独立储能元件指定一个变量作为状态变量。
②根据具体的控制系统,应用其物理规律,列写出描述系统动态过程的一阶微分方程组,写成矩阵的形式,即得到系统的状态方程,再根据物理规律列写输出方程,即可得到状态空间表达式。
(3)举例:
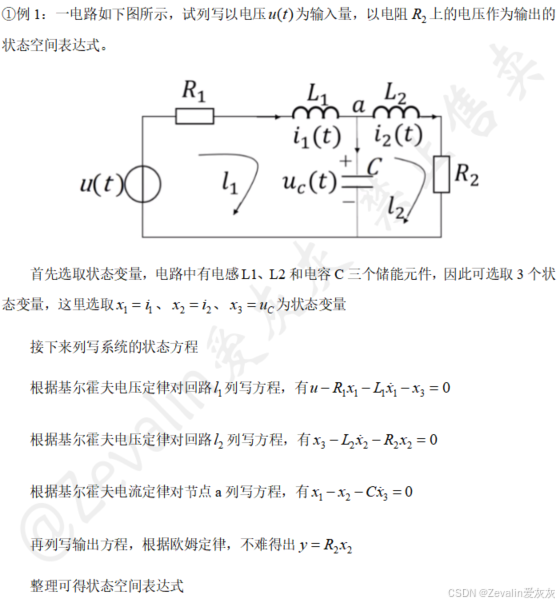
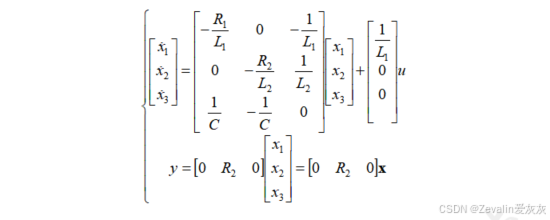


3、根据传递函数或高阶微分方程得到状态空间表达式
(1)对系统动态过程的描述,可以分为内部描述和外部描述。
①控制系统的外部描述------描述控制系统的外部特征,即描述系统的输入、输出关系,如传递函数和高阶微分方程。
②控制系统的内部描述------不仅可以描述系统的输入输出关系,而且还能够揭示出系统内部各变量的关联关系,如系统的状态空间表达式。
③系统的内部描述和外部描述在满足一定条件下是可以相互转换的。
(2)由输入输出描述确定状态空间描述的问题称为实现问题。
①实现问题的具体说明:

②实现存在的条件为。


③实现具有非唯一性,会有无穷多个状态空间表达式,实现给定的输入输出关系。
④没有零极点对消的传递函数的实现称为最小实现(因为没有零极点对消的传递函数,求得的状态空间表达式的维数是最小的,也就是说,传递函数的零极点对消,能够降低传递函数的阶数和其对应的状态空间表达式的维数)。
(3)单输入单输出系统的实现方法一:
①实现方法步骤:




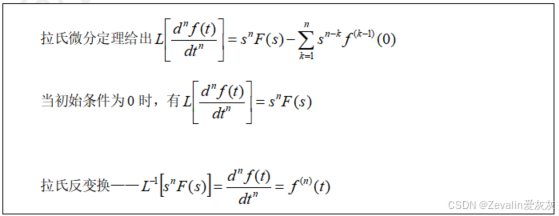
②举例:



(4)单输入单输出系统的实现方法二:
①实现方法步骤:








②举例:

(5)多输入多输出系统的实现方法:
①多输入多输出系统的实现,可采用方框图法,就是依据高阶微分方程组,画出所对应的方框图,再根据方框图列写状态空间表达式。
②由于经典控制理论难以有效地处理多输入多输出系统,通常不会建立多输入多输出系统的微分方程或传递函数描述。
三、状态向量的线性变换
1、状态空间表达式的非唯一性
(1)基于先前的介绍,可得状态向量有如下特点,它们说明了同一系统不同状态向量之间必然存在一种线性变换的关系。
①状态变量是足以完全表征系统运动状态的最小个数的一组变量。
②状态变量是相互独立的,它们不能被互相线性表示。
③同一系统状态变量的个数是唯一确定的。
④同一系统状态变量的选取是非唯一的。
(2)证明:同一系统不同状态向量之间必然存在一种线性变换的关系。

(3)证明:状态空间表达式具有非唯一性。

(4)举例:

2、系统特征值的不变性
(1)系统的性能主要由传递函数的极点决定,也就是由系统特征方程的系数决定;而系统矩阵的特征根与传递函数的极点对应,因此在现代控制理论中,决定系统性能的主要是系统矩阵的特征值。
(2)系统状态空间表达式中系统矩阵A的特征值称为系统的特征值。

(3)证明:对状态变量做非奇异线性变换(即与可逆矩阵相乘),不会改变系统的特征值。

3、对角规范型
(1)系统的特征向量概念:

(2)对角规范型状态方程:


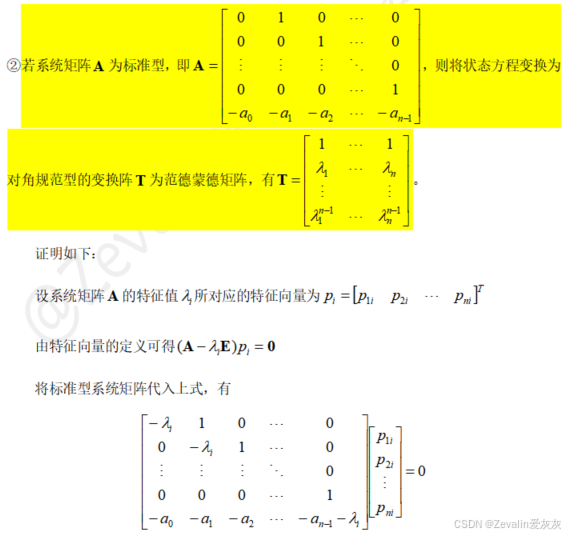

(3)在对角规范型下,各状态变量间实现了完全解耦,可表示为几个独立的状态变量方程。
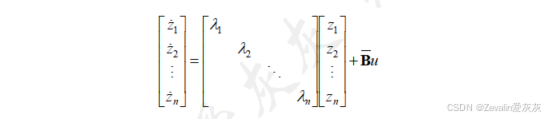
(4)举例:



4、约当规范型
(1)特征根的代数重数和几何重数概念:

(2)系统的广义特征向量概念:

(3)约当标准型概念:
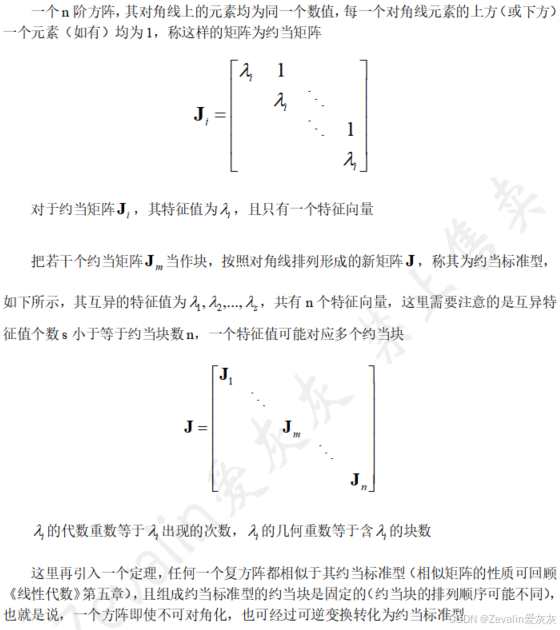


(4)约当规范型状态方程:

(5)当系统矩阵的特征值有重根时,通常不可能通过线性变换而实现状态变量之间的完全解耦,约当规范型是可能达到的最简耦合形式。同一特征根、同一约当子块所对应的状态变量之间存才在耦合关系。
四、从状态空间表达式求传递函数矩阵及组合系统的状态空间表达式
1、从状态空间表达式求传递函数矩阵
(1)传递函数矩阵的定义:

(2)由状态空间表达式导出传递函数矩阵:


2、传递函数矩阵的唯一性
(1)一个系统的状态空间表达式是非唯一的,但其传递函数矩阵是唯一的。
(2)证明:

3、组合系统的状态空间表达式
(1)由两个或两个以上的子系统按照一定方式联接构成的系统称为组合系统。
(2)构建组合系统数学模型的基本思路:
①确定子系统可组合的条件,即确定各子系统联接的输入输出维数是否匹配。
②找出联接的各子系统间、子系统与组合系统间的输入输出关系。
③根据各子系统与组合系统的输入输出关系,导出组合系统的状态空间表达式与传递函数矩阵。
(3)组合系统的基本组合方式可分为串联、并联和反馈三种类型。
①子系统并联:

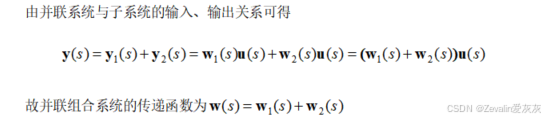
②子系统串联:

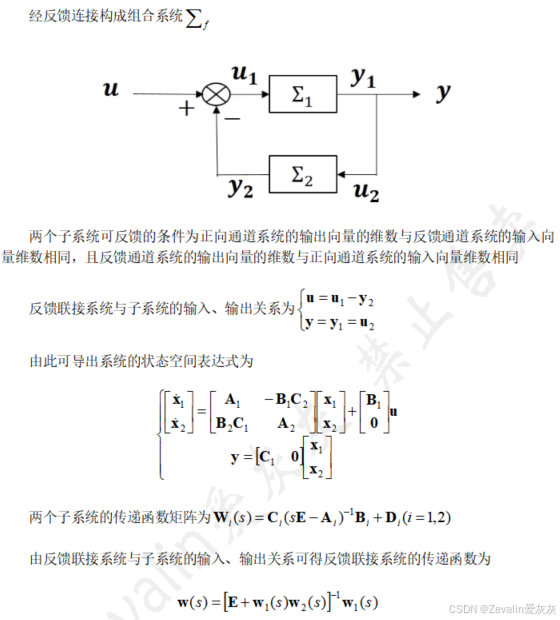
③子系统反馈联接:
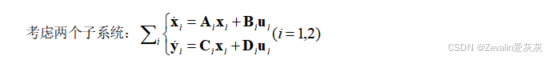
五、离散时间系统、时变系统和非线性系统的状态空间表达式
1、离散时间系统
离散时间系统的状态空间表达式可用差分方程组表示为
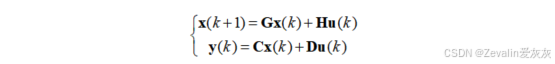
离散时间系统和连续时间系统的处理方式是类似的,连续系统使用微分方程对应离散系统使用差分方程,连续系统使用连续传递函数对应离散系统使用离散传递函数
2、线性时变系统
线性时变系统的状态空间表达式可表示为
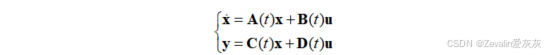
其系数矩阵的元素中至少有一个元素是时间t的函数
3、非线性系统
(1)非线性时变系统:
非线性时变系统的状态空间表达式可表示为
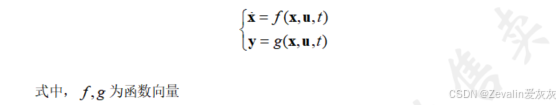
(2)非线性定常系统:
当非线性系统的状态空间表达式中不显含时间t时,则称为非线性定常系统,非线性定常系统的状态空间表达式可表示为

(3)非线性系统的线性化:

