【算法训练营Day32】图论专题

十八岁讨厌编程2026-01-15 13:45

文章目录

图论基础

图论理论基础

DFS

核心思想：走到底（目标）之后再回溯

代码框架类似于我们前面说的回溯算法的框架：

java 复制代码 
void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

从而我们可以衍生出深搜三要素：

  • 确认递归参数
  • 确认终止条件
  • 处理目前节点出发的路径（通常是for循环且伴有回溯）

所有可达路径

题目链接：98. 可达路径

解题逻辑：

dfs是一个比较广泛的算法，例如我们前面的二叉树的遍历，它属于dfs在二叉树中的应用，以及前面的回溯算法，它也属于dfs的一种。这也就是为什么回溯算法的模板和dfs非常的相似。

代码如下：

java 复制代码 
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int a = in.nextInt();
        int b = in.nextInt();
        List<Integer>[] bucket = new LinkedList[a];
        for (int i = 0; i < a; i++) bucket[i] = new LinkedList<Integer>();
        while (b-- > 0) {
            int num1 = in.nextInt();
            int num2 = in.nextInt();
            bucket[num1 - 1].add(num2);
        }

        path.add(1);
        dfs(bucket, 1, a);

        if (result.size() == 0) System.out.println(-1);
        for (List<Integer> path : result) {
            StringBuffer ss = new StringBuffer();
            for (Integer num : path) {
                ss.append(num).append(" ");
            }
            System.out.println(ss.substring(0, ss.length() - 1).toString());
        }
    }

    static List<List<Integer>> result = new ArrayList<>();
    static List<Integer> path = new ArrayList<>();

    public static void dfs(List<Integer>[] bucket, Integer item, Integer end) {
        if (item == end) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (Integer num : bucket[item - 1]) {
            path.add(num);
            dfs(bucket, num, end);
            path.remove(path.size() - 1);
        }
    }
}

BFS

广度优先算法：是一种波纹状的搜索算法，一圈一圈向外递进

在二叉树的遍历中的层序遍历就是bfs在树形结构中的应用。

bfs不需要显式的递归，而是需要借助一个额外的数据结构帮我们存储数据，这个数据结构可以是队列，也可以是栈、数组等线性数据结构。

bfs的代码模板如下：

java 复制代码 
import java.util.LinkedList;
import java.util.Queue;

public class BFSExample {
    // 表示四个方向：右、下、上、左
    private static final int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};
    
    /**
     * BFS搜索算法
     * @param grid 地图，二维字符数组
     * @param visited 标记访问过的节点
     * @param x 开始搜索的x坐标
     * @param y 开始搜索的y坐标
     */
    public static void bfs(char[][] grid, boolean[][] visited, int x, int y) {
        // 定义队列，使用LinkedList实现Queue接口
        Queue<int[]> queue = new LinkedList<>();
        // 起始节点加入队列
        queue.offer(new int[]{x, y});
        // 标记为已访问
        visited[x][y] = true;
        
        // 队列不为空时继续遍历
        while (!queue.isEmpty()) {
            // 取出队首元素
            int[] cur = queue.poll();
            int curx = cur[0];
            int cury = cur[1];
            
            // 遍历四个方向
            for (int i = 0; i < 4; i++) {
                int nextx = curx + dir[i][0];
                int nexty = cury + dir[i][1];
                
                // 检查坐标是否越界
                if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) {
                    continue;
                }
                
                // 如果节点未被访问过
                if (!visited[nextx][nexty]) {
                    // 加入队列
                    queue.offer(new int[]{nextx, nexty});
                    // 标记为已访问
                    visited[nextx][nexty] = true;
                }
            }
        }
    }
}

孤岛计数

题目链接：99. 计数孤岛

同Leetcode：200. 岛屿数量

解题逻辑：遍历整张图，如果该点为陆地且未被搜索过，则岛个数加1，然后将该点及周围的岛全部搜索干净（标记为搜索过），然后继续往下遍历，遇到海洋跳过，遇到搜索了的岛跳过，如此直到遍历完整张图。

DFS版

java 复制代码 
import java.util.*;

public class Main{
    public static void main(String[] args){
        Scanner in = new Scanner(System.in);
        int a = in.nextInt();
        int b = in.nextInt();
        //记录图
        int[][] map = new int[a][b];
        int[][] record = new int[a][b];
        for(int i = 0;i < a;i++){
            for(int j = 0;j < b;j++) {
                map[i][j] = in.nextInt();
            }
        }

        int count = 0;
        //开始遍历
        for(int i = 0;i < a;i++){
            for(int j = 0;j < b;j++) {
                if(map[i][j] == 0 || record[i][j] == 1) continue;
                count++;
                dfs(map,record,i,j,a,b);
            }
        }
        System.out.println(count);
    }

    // 表示四个方向：右、下、上、左
    private static final int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};

    public static void dfs(int[][] map,int[][] record,int x,int y,int limitx,int limity){

        if(x < 0 || y < 0 || x >= limitx || y >= limity || record[x][y] == 1 || map[x][y] == 0) return;

        record[x][y] = 1;

        for(int i = 0;i < dir.length;i++) {
            int nextx = x + dir[i][0];
            int nexty = y + dir[i][1];

            dfs(map,record,nextx,nexty,limitx,limity);

        }


    }
}

BFS版

java 复制代码 
import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean[][] record = new boolean[m][n];
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        int count = 0;;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(!record[i][j] && map[i][j] == 1) {
                    count++;
                    bfs(map, record, i, j);
                }
            }
        }
        System.out.println(count);
    }
    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static void bfs(int[][] map, boolean[][] record, int x, int y) {
        Deque<int[]> queue = new ArrayDeque<>();
        queue.offer(new int[]{x,y});
        record[x][y] = true;
        while(queue.size() > 0) {
            int[] pos = queue.poll();
            for(int i = 0; i < 4; i++) {
                int curX = pos[0] + dire[i][0];
                int curY = pos[1] + dire[i][1];
                if(curX < 0 || curY < 0 || curX >= map.length || curY >= map[0].length) continue;
                if(!record[curX][curY] && map[curX][curY] == 1) {
                    queue.offer(new int[]{curX,curY});
                    record[curX][curY] = true;
                }
            }
        }
    }
}

岛屿的最大面积

题目链接：100. 最大岛屿的面积

解题逻辑：

本题使用DFS进行解决，BFS可自行探索。

解题代码：

java 复制代码 
import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean[][] record = new boolean[m][n];
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        int max = 0;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(!record[i][j] && map[i][j] == 1) {
                    int area = dfs(map, record, i, j,1);
                    if(area > max) max = area;
                }
            }
        }
        System.out.println(max);
    }
    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static int dfs(int[][] map, boolean[][] record, int x, int y,int area) {
        if(x < 0 || y < 0 || x >= map.length || y >= map[0].length || record[x][y] || map[x][y] == 0) return area - 1;

        record[x][y] = true;
        
        for(int i = 0; i < 4; i++) {
            int curX = x + dire[i][0];
            int curY = y + dire[i][1];
            area = dfs(map, record, curX, curY, area + 1);
        }
        return area;
    }
}

孤岛的总面积

题目链接：101. 孤岛的总面积

解题逻辑：

在上一题的基础上加上一个孤岛判断的逻辑（使用类变量），如果不是孤岛，那么不计入到孤岛总面积中。

解题代码：

java 复制代码 
import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean[][] record = new boolean[m][n];
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        int total = 0;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(!record[i][j] && map[i][j] == 1) {
                    flag = true;
                    int area = dfs(map, record, i, j,1);
                    if(flag) total += area;
                }
            }
        }
        System.out.println(total);
    }
    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static boolean flag = true;

    public static int dfs(int[][] map, boolean[][] record, int x, int y,int area) {
        if(x < 0 || y < 0 || x >= map.length || y >= map[0].length || record[x][y] || map[x][y] == 0) return area - 1;

        record[x][y] = true;

        if(x == 0 || x == map.length - 1 || y == 0 || y == map[0].length - 1) flag = false;
        
        for(int i = 0; i < 4; i++) {
            int curX = x + dire[i][0];
            int curY = y + dire[i][1];
            area = dfs(map, record, curX, curY, area + 1);
        }
        return area;
    }
}

沉没孤岛

题目链接：102. 沉没孤岛

解题逻辑：

在上一题的基础上，将孤岛的坐标收集起来，最后集体沉默就可以了

解题代码：

java 复制代码 
import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean[][] record = new boolean[m][n];
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(!record[i][j] && map[i][j] == 1) {
                    flag = true;
                    dfs(map, record, i, j);
                    if(flag) allIsland.add(new ArrayList<>(thisIsland));
                    thisIsland.clear();
                }
            }
        }
        for(List<int[]> island : allIsland) {
            for(int[] point : island) {
                map[point[0]][point[1]] = 0;
            }
        }
        for(int[] row : map) {
            for(int narrow : row) {
                System.out.print(narrow + " ");
            }
            System.out.println();
        }
    }
    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static boolean flag = true;

    public static List<int[]> thisIsland = new ArrayList<>();

    public static List<List<int[]>> allIsland = new ArrayList<>();

    public static void dfs(int[][] map, boolean[][] record, int x, int y) {
        if(x < 0 || y < 0 || x >= map.length || y >= map[0].length || record[x][y] || map[x][y] == 0) return;

        record[x][y] = true;

        thisIsland.add(new int[]{x, y});

        if(x == 0 || x == map.length - 1 || y == 0 || y == map[0].length - 1) flag = false;
        
        for(int i = 0; i < 4; i++) {
            int curX = x + dire[i][0];
            int curY = y + dire[i][1];
            dfs(map, record, curX, curY);
        }
    }
}

高山流水

题目链接：103. 高山流水

解题逻辑：

依旧使用dfs模拟走路，与前面一题的区别在于：

  • 走路的逻辑发生变化，下一步还需判断高度是否小于等于当前高度
  • 在对起点进行遍历的时候，需要刷新记录，因为每个起点的路径是互不影响的

解题代码：

java 复制代码 
import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean[][] record = new boolean[m][n];
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                flag = new boolean[2];
                record = new boolean[m][n];
                if(dfs(map, record, i, j)) results.add(new int[]{i, j});
            }
        }
        for(int[] result : results) {
            System.out.println(result[0] + " " + result[1]);
        }

        
    }
    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static List<int[]> results = new ArrayList<>();

    public static boolean[] flag = new boolean[2];

    public static boolean dfs(int[][] map, boolean[][] record, int x, int y) {
        record[x][y] = true;

        if(x == 0 || y == 0) flag[0] = true;
        
        if(x == map.length - 1 || y == map[0].length - 1) flag[1] = true;

        if(flag[0] && flag[1]) return true;
        
        for(int i = 0; i < 4; i++) {
            int curX = x + dire[i][0];
            int curY = y + dire[i][1];
            if(curX < 0 || curY < 0 || curX >= map.length || curY >= map[0].length || record[curX][curY]) continue;
            if(map[x][y] < map[curX][curY]) continue;
            boolean ret = dfs(map, record, curX, curY);
            if(ret) return true;
        }
        
        return false;
    }
}

建造最大岛屿

题目链接：104. 建造最大岛屿

解题逻辑：

我们使用搜索（dfs、bfs均可，本题使用bfs）将现有的岛屿做一个染色，同时记录每一个岛屿的大小。然后再遍历每一块水域，如果与岛屿相邻则进行的累加，如此选出最大的岛屿面积。

易错点：在遍历水域的时候，由于水域可能会被岛屿环绕，所以可能会将该岛屿的面积累加多次，所以这里要根据岛屿编号进行去重。

解题代码：

java 复制代码 
import java.util.*;

public class Main{
        public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        boolean[][] record = new boolean[m][n];
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        Map<Integer,Integer> islands = new HashMap<>();
        int islandNum = 2;        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(record[i][j] || map[i][j] == 0) continue;
                int area = bfs(map, record, i, j, islandNum);
                islands.put(islandNum, area);
                islandNum++;
            }
        }
        int max = 0;
        for(Integer val : islands.values()) if(val > max) max = val;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(map[i][j] == 0) {
                    int sum = 1;
                    Set<Integer> set = new HashSet<>();
                    for(int k = 0; k < 4; k++) {
                        int curX = i + dire[k][0];
                        int curY = j + dire[k][1];
                        if(curX < 0 || curY < 0 || curX >= map.length || curY >= map[0].length || map[curX][curY] == 0 || set.contains(map[curX][curY])) continue;
                        int area = islands.get(map[curX][curY]);
                        sum += area;
                        set.add(map[curX][curY]);
                    }
                    if(sum > max) max = sum;
                }
            }
        }
        System.out.println(max);

    }
    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static int bfs(int[][] map, boolean[][] record, int x, int y, int islandNum) {
        Deque<int[]> queue = new ArrayDeque<>();
        queue.offer(new int[]{x, y});
        int area = 0;
        record[x][y] = true;
        map[x][y] = islandNum;
        area++;
        while(!queue.isEmpty()) {
            int[] cur = queue.poll();
            x = cur[0];
            y = cur[1];
            for(int i = 0; i < 4; i++) {
                int curX = x + dire[i][0];
                int curY = y + dire[i][1];
                if(curX < 0 || curY < 0 || curX >= map.length || curY >= map[0].length || record[curX][curY] || map[curX][curY] == 0) continue;
                queue.offer(new int[]{curX, curY});
                record[curX][curY] = true;
                map[curX][curY] = islandNum;
                area++;
            }
        }
        return area;
    }
}

岛屿的周长

题目链接：106. 海岸线计算

解题思路：

本题转化一下也就是说：岛屿四周靠海的边有多少条？也就是说我们只需要遍历找到岛屿的格子，然后判断他的哪几条边靠海，然后进行累加就可以得到结果。

解题代码：

java 复制代码 
import java.util.*;

public class Main{

    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int m = in.nextInt();
        int n = in.nextInt();
        int[][] map = new int[m][n];
        for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) map[i][j] = in.nextInt();
        int result = 0;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(map[i][j] == 1) {
                    for(int k = 0; k < 4; k++) {
                        int curX = i + dire[k][0];
                        int curY = j + dire[k][1];
                        if(curX < 0 || curY < 0 || curX >= map.length || curY >= map[0].length || map[curX][curY] == 0) result++;
                    }
                }
            }
        }
        System.out.println(result);

    }
}

腐烂的橘子

题目链接：994. 腐烂的橘子

解题逻辑：

这道题的本质就是考察bfs的扩散轮数：每一轮遍历开始前，先获取当前队列的元素总数 size，然后循环 size 次，这 size 个元素就是「当前层的所有节点」，处理完这一层，扩散次数就 +1。

解题代码：

java 复制代码 
class Solution {
    public int orangesRotting(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        boolean[][] record = new boolean[m][n];
        int result = bfs(grid, record);
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(grid[i][j] == 1) {
                    return -1;
                }
            }
        }
        return result;
    }

    public static int[][] dire = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public int bfs(int[][] grid, boolean[][] record) {
        Deque<int[]> queue = new ArrayDeque<>();
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(grid[i][j] == 2) {
                    queue.offer(new int[]{i, j});
                    record[i][j] = true;
                }
            }
        }
        int time = 0;
        int offset;
        while(!queue.isEmpty()) {
            offset = queue.size();
            for (int k = 0; k < offset; k++) {
                int[] posi = queue.poll();
                for(int i = 0; i < 4; i++) {
                    int curX = posi[0] + dire[i][0];
                    int curY = posi[1] + dire[i][1];
                    if(curX < 0 || curY < 0 || curX >= grid.length || curY >= grid[0].length || record[curX][curY] || grid[curX][curY] == 0 || grid[curX][curY] == 2) continue;
                    queue.offer(new int[]{curX, curY});
                    record[curX][curY] = true;
                    grid[curX][curY] = 2;
                }
            }
            if(!queue.isEmpty()) time++;
        }
        return time;
    }
}

课程表（拓扑排序）

题目链接：207. 课程表

给出一个 有向图，把这个有向图转成线性的排序 就叫拓扑排序

拓扑排序的核心就是不断找入度为0的节点，然后再将这些节点删去，再重新寻找入度为0的节点，如此循环往复即可。

拓扑排序使用广搜（BFS）更加简单常用。如果最终结果集中的元素个数和所给的元素个数不一样，那么就说明有向图成环了！此时拓扑排序是无法完成的。

这之间有两个数据结构发挥了巨大的作用：

  • 使用邻接表记录课程之间的关系
  • 使用列表存储每个课程的入度

解题代码：

java 复制代码 
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int[] inDegree = new int[numCourses];
        List<List<Integer>> graph = new ArrayList<>();
        for(int i = 0; i < numCourses; i++) graph.add(new ArrayList<>());
        for(int[] item : prerequisites) {
            inDegree[item[0]]++;
            graph.get(item[1]).add(item[0]);
        }
        int count = 0;
        Deque<Integer> queue = new ArrayDeque<>();
        for(int i = 0; i < numCourses; i++) if(inDegree[i] == 0) queue.offer(i);
        while(!queue.isEmpty()) {
            int cur = queue.poll();
            count++;
            for(int lesson : graph.get(cur)) {
                inDegree[lesson]--;
                if(inDegree[lesson] == 0) queue.offer(lesson);
            }
        }
        if(count == numCourses) return true;
        return false;
    }
}

实现 Trie (前缀树、字典树)

题目链接：208. 实现 Trie (前缀树)

解题逻辑：

字典树的构造就是将所给字符串拆成单个的字符，依次连接前一个结点形成一棵多叉树。

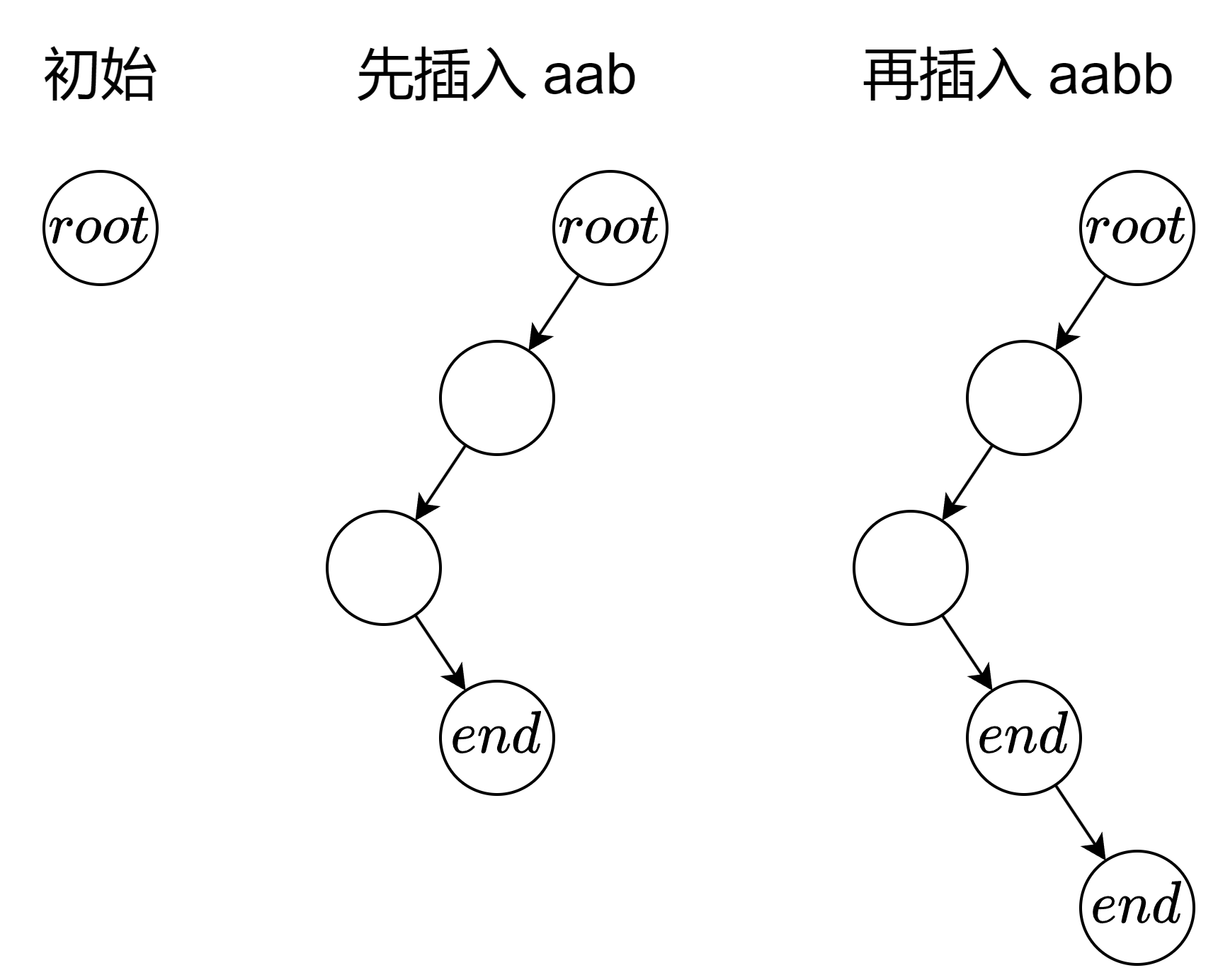
每个节点存储下一个节点的数组以及是否为结尾的标记。

解题代码：

java 复制代码 
class Trie {
    class Node{
        Node[] nodes = new Node[26];
        boolean isEnd = false;
    }

    private Node root = new Node();

    public Trie() {
    }
    
    public void insert(String word) {
        Node prefix = root;
        for(char c : word.toCharArray()) {
            if(prefix.nodes[c - 'a'] == null) prefix.nodes[c - 'a'] = new Node();
            prefix = prefix.nodes[c - 'a'];
        }
        prefix.isEnd = true;
    }
    
    public boolean search(String word) {
        Node prefix = root;
        for(char c : word.toCharArray()) {
            if(prefix.nodes[c - 'a'] == null) return false;
            prefix = prefix.nodes[c - 'a'];
        }
        return prefix.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        Node pre = root;
        for(char c : prefix.toCharArray()) {
            if(pre.nodes[c - 'a'] == null) return false;
            pre = pre.nodes[c - 'a'];
        }
        return true;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */
相关推荐
小欣加油2 小时前
leetcode 174 地下城游戏
c++·算法·leetcode·职场和发展·动态规划
sali-tec2 小时前
C# 基于OpenCv的视觉工作流-章11-高斯滤波
图像处理·人工智能·opencv·算法·计算机视觉
不知名XL2 小时前
day23 贪心算法 part01
算法·贪心算法
wuqingshun3141593 小时前
蓝桥杯 缺页异常2【算法赛】
算法·职场和发展·蓝桥杯
Mh_ithrha3 小时前
题目：小鱼比可爱（java）
java·开发语言·算法
l1t3 小时前
数独优化求解C库tdoku-lib的使用
c语言·开发语言·python·算法·数独
有一个好名字3 小时前
力扣-奇偶链表
算法·leetcode·链表
wxm6313 小时前
力扣算法题（C++）：1、2
java·算法·leetcode
im_AMBER3 小时前
Leetcode 103 反转链表 II
数据结构·c++·笔记·学习·算法·leetcode
热门推荐
01GitHub 镜像站点02网站改了域名，如何查找？03Linux下V2Ray安装配置指南04Labelme从安装到标注：零基础完整指南05AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07UV安装并设置国内源08百度网盘偷偷给电脑“降频”？09Claude Code Skills 实用使用手册102025-04-03 Latex学习1——本地配置Latex + VScode环境