前面我们讲了 ALS 和 SGD,它们像是"填空题高手",拼命去猜矩阵里空的格子。
而 SVD(奇异值分解,Singular Value Decomposition) ,则是数学界真正的"贵族"。它不只是为了填空,更是为了透视。
如果说矩阵分解是把"大象"装进冰箱,SVD 就是那个不仅能装进去,还能精确告诉你大象由多少骨头、多少肉组成的"CT扫描仪"。
本文,我们用最直观的方式,看看 SVD 是如何把复杂的数据完美"拆解"的。
1. 核心思想:数据的"三棱镜"
你一定学过物理:一束白光射向三棱镜,会被分解成"赤橙黄绿青蓝紫"七种单色光。
SVD 就是数据的三棱镜。
它认为,你那张乱七八糟的用户评分表(矩阵 AAA),虽然看起来复杂,但其实是由三个极其整齐、纯粹的矩阵相乘得来的。
公式 : A=U×Σ×VTA = U \times \Sigma \times V^TA=U×Σ×VT
这三个矩阵分别代表什么?我们用"电影推荐"的例子来翻译一下:
- 左矩阵 UUU (User-Concept) :
- 含义 :"用户-偏好"关系表。
- 例子:张三对"动作概念"的喜爱度、对"爱情概念"的喜爱度。
- 中间矩阵 Σ\SigmaΣ (Strength) :
- 含义 :"概念强度"表(奇异值)。
- 特点 :它是一个对角矩阵(只有对角线有数,其他全0)。
- 例子 :它告诉我们,"动作"这个概念在整个数据库里有多重要,"爱情"有多重要。数值越大,代表这个特征越核心(主要矛盾)。
- 右矩阵 VTV^TVT (Concept-Item) :
- 含义 :"概念-电影"关系表。
- 例子:《战狼》里含多少"动作概念",《泰坦尼克》里含多少"爱情概念"。
2. 小猪佩奇 vs 蒙娜丽莎:目标函数是什么?
SVD 既然是数学解析解,它有"目标函数"吗?
有的。SVD 的精髓在于**"有损压缩"**(低秩近似)。
2.1 完美的代价
数学上的 SVD 可以无损 还原原始矩阵(只要特征维度足够多)。但这没意义!我们要的是过滤噪声,提取精华 。
比如,一张 4K 的高清照片,有些细节(噪点)是没用的。
2.2 截断 SVD (Truncated SVD)
我们要做的,是只保留 Σ\SigmaΣ 矩阵里最大的那几个人(比如前 10 个奇异值),把剩下那些很小的数值(代表不重要的细节、噪声)统统划掉变成 0。
这就引出了 SVD 的隐式目标函数:
目标 :找到一个简化版的矩阵,使得它和原始矩阵的差距最小。
min∥A−Aapprox∥2\min \| A - A_{approx} \|^2min∥A−Aapprox∥2
- AAA:原始的高清大图(满是数据)。
- AapproxA_{approx}Aapprox:只保留了主要特征的缩略图。
直白理解 :
我们要画一幅《蒙娜丽莎》,SVD 告诉我们:先把脸部轮廓(最大的奇异值)画好,再画五官(中等奇异值),最后才是背景的树叶(最小的奇异值)。
如果我们只画前两步 ,虽然丢失了树叶细节,但依然能一眼认出这是蒙娜丽莎,而且画画的速度快了100倍!
3. 图解 SVD 分解过程
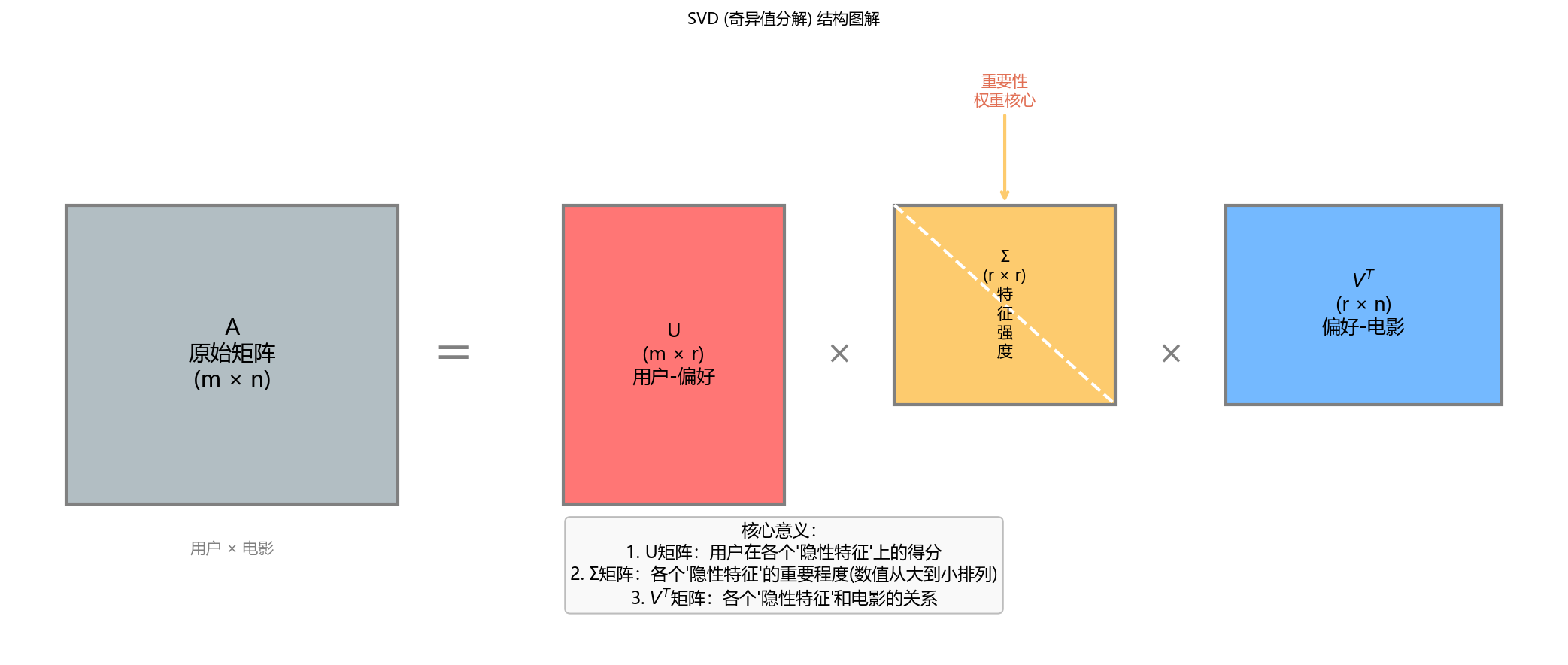
4. 既然 SVD 这么强,为啥推荐系统里还得用 ALS?
这就要说到 SVD 的死穴了。
SVD 的洁癖
标准 SVD 数学公式要求矩阵必须是稠密的(Dense) ,也就是说,不能有空格!
- 但现实中,用户评分表 99% 都是空的(没人看完所有电影)。
- 如果要用标准 SVD,必须先把空格随便填满(比如填0,或填平均分)。这会引入巨大的人为误差,而且计算量大到内存爆炸。
变种:FunkSVD
所以,我们在推荐系统里常说的"SVD",其实往往指 FunkSVD 。
它借用了 SVD "矩阵 U×VU \times VU×V" 的思想 ,但抛弃了复杂的数学求解,改用 SGD(梯度下降) 来一个格子一个格子地把数字"凑"出来(允许有空格)。
5. 总结
- SVD :是矩阵分解的鼻祖 和数学基石。
- 三大件 :它把数据拆解为 用户特征(UUU) 、特征强度(Σ\SigmaΣ) 、物品特征(VVV)。
- 目标函数 :寻找最佳的低维近似(用最少的信息量,还原最真实的原始数据)。
- 应用 :除了推荐系统,还广泛用于图片压缩 、降噪 、PCA降维。
SVD 就像一个高明的画家,它懂得取舍,知道什么才是数的"灵魂"。