通过一到多个特征,对数据的值进行预测。
# 房价预测
特征:[面积, 卧室数, 地理位置评分]
目标:房价
# 销量预测
特征:[广告投入, 季节因素, 促销力度]
目标:销售量1. 数据与问题设定
我们使用一个可以手算的小数据集:
数据表(n=5, p=4):
| 样本 | x₁ | x₂ | x₃ | x₄ | y |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 2 |
| 2 | 0 | 2 | 1 | 0 | 5 |
| 3 | 1 | 1 | 1 | 1 | 6 |
| 4 | 0 | 1 | 2 | 0 | 7 |
| 5 | 1 | 0 | 1 | 2 | 4 |
模型:
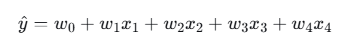
其中 w0 是截距(bias),w1∼w4 是特征权重。
2. 损失函数(均方误差MSE)
对于 m 个样本:
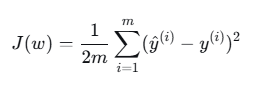
通常使用 1/(2m) 而不是 1/m 是为了梯度计算时消去系数2。
3. 梯度计算公式
对每个参数 wj:
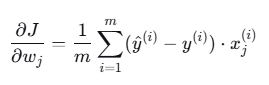
其中对于 j=0(截距 w0),约定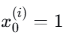 。
。
所以:
-
对 w0:
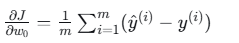
-
对 wj,j≥1:
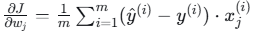
4. 参数初始化
随机初始化权重(为方便手算,我们取简单值):
w0=0.5,w1=0.5,w2=0.5,w3=0.5,w4=0.5
学习率 α=0.1。
5. 第1轮迭代计算
步骤1:计算预测值 y^(i)
对于每个样本 i:
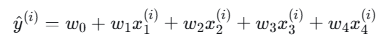
样本1:x=[1,0,0,1],y=2
y^(1)=0.5+0.5×1+0.5×0+0.5×0+0.5×1=0.5+0.5+0+0+0.5=1.5
样本2:x=[0,2,1,0],y=5
y^(2)=0.5+0.5×0+0.5×2+0.5×1+0.5×0=0.5+0+1.0+0.5+0=2.0
样本3:x=[1,1,1,1],y=6
y^(3)=0.5+0.5×1+0.5×1+0.5×1+0.5×1=0.5+0.5+0.5+0.5+0.5=2.5
样本4:x=[0,1,2,0],y=7
y^(4)=0.5+0.5×0+0.5×1+0.5×2+0.5×0=0.5+0+0.5+1.0+0=2.0
样本5:x=[1,0,1,2],y=4
y^(5)=0.5+0.5×1+0.5×0+0.5×1+0.5×2=0.5+0.5+0+0.5+1.0=2.5
预测值向量:y^=[1.5,2.0,2.5,2.0,2.5]
步骤2:计算误差 e(i)=y^(i)−y(i)
e(1)=1.5−2=−0.5 e(2)=2.0−5=−3.0 e(3)=2.5−6=−3.5 e(4)=2.0−7=−5.0 e(5)=2.5−4=−1.5
误差向量:e=[−0.5,−3.0,−3.5,−5.0,−1.5]
步骤3:计算每个参数的梯度(BGD/FGD全梯度下降)
梯度公式:
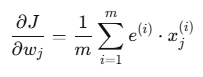
其中 m=5,x0(i)=1。
- 截距 w0 的梯度:
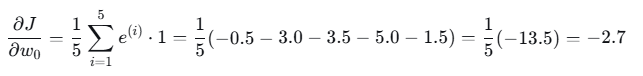
- w1 的梯度:
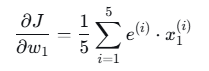
需要 x1 列:[1,0,1,0,1]
计算点积:(−0.5×1)+(−3.0×0)+(−3.5×1)+(−5.0×0)+(−1.5×1)
= −0.5+0−3.5+0−1.5=−5.5−0.5+0−3.5+0−1.5=−5.5
梯度:−5.5/5=−1.1
- w2 的梯度:
x2列=[0,2,1,1,0]
点积:(−0.5×0)+(−3.0×2)+(−3.5×1)+(−5.0×1)+(−1.5×0)
= 0−6.0−3.5−5.0+0=−14.50−6.0−3.5−5.0+0=−14.5
梯度:−14.5/5=−2.9
- w3 的梯度:
x3列=[0,1,1,2,1]
点积:(−0.5×0)+(−3.0×1)+(−3.5×1)+(−5.0×2)+(−1.5×1)
= 0−3.0−3.5−10.0−1.5=−18.00−3.0−3.5−10.0−1.5=−18.0
梯度:−18.0/5=−3.6
- w4 的梯度:
x4列=[1,0,1,0,2]
点积:(−0.5×1)+(−3.0×0)+(−3.5×1)+(−5.0×0)+(−1.5×2)
= −0.5+0−3.5+0−3.0=−7.0−0.5+0−3.5+0−3.0=−7.0
梯度:−7.0/5=−1.4
梯度向量:∇J=[−2.7,−1.1,−2.9,−3.6,−1.4]
步骤4:参数更新
更新公式: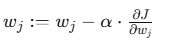
学习率 α=0.1:
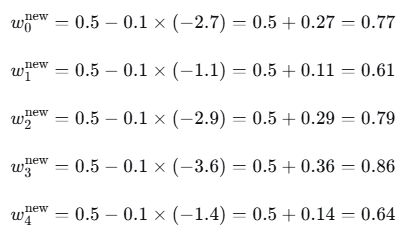
第1轮结束后的参数:
w=[0.77,0.61,0.79,0.86,0.64]
6. 第2轮迭代(快速计算)
用新权重计算预测值:

误差:
e=[2.02−2,3.21−5,3.67−6,3.28−7,3.52−4]=[0.02,−1.79,−2.33,−3.72,−0.48]
计算梯度(简略过程,与上面第一轮计算方法一样):
-
截距梯度:
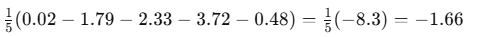
-
w1梯度:
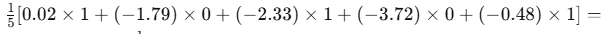
-
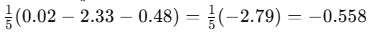
-
类似计算其他...
更新参数(学习率0.1):
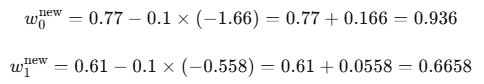
(其他参数类似更新)
7. 损失值变化
第1轮损失(MSE):
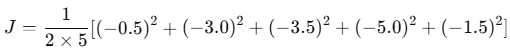
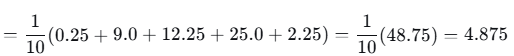
第2轮损失:
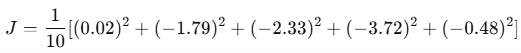
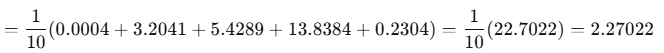
损失明显下降,说明梯度下降有效。
8.迭代停止情况
early stopping 用来决定"梯度下降什么时候停" 的方法,通常基于:
- 验证集损失J(validation loss)不再下降(或开始上升)
- 验证集准确率/指标达到峰值后连续几 epoch 没提升
- 训练 loss 下降但验证 loss 上升(过拟合信号)
9.代码实现上面计算流程
1.手动实现
python
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans'] # 中文支持
plt.rcParams['axes.unicode_minus'] = False
# ======================
# 1. 数据准备
# ======================
X = np.array([
[1, 0, 0, 1],
[0, 2, 1, 0],
[1, 1, 1, 1],
[0, 1, 2, 0],
[1, 0, 1, 2]
])
y = np.array([2, 5, 6, 7, 4])
# 为了让截距项 w0 参与计算,添加一列全 1
X_b = np.c_[np.ones((X.shape[0], 1)), X] # shape: (5, 5)
# ======================
# 2. 手动实现批量梯度下降
# ======================
def batch_gradient_descent(X_b, y, alpha=0.1, n_iterations=1000, tol=1e-6):
m = X_b.shape[0]
theta = np.array([0.5] * X_b.shape[1]) # 初始化
loss_history = []
for iteration in range(n_iterations):
# 前向传播:预测值
y_hat = X_b.dot(theta)
# 误差
errors = y_hat - y
# 损失(MSE)
loss = np.mean(errors ** 2) / 2
loss_history.append(loss)
# 梯度
gradients = (1/m) * X_b.T.dot(errors)
# 更新参数
theta_new = theta - alpha * gradients
# 判断是否收敛(可选)
if np.all(np.abs(theta_new - theta) < tol):
print(f"收敛于第 {iteration} 次迭代")
break
theta = theta_new
return theta, loss_history
# 运行手动梯度下降
theta_manual, loss_manual = batch_gradient_descent(X_b, y, alpha=0.1, n_iterations=2000)
print("\n手动梯度下降结果:")
print("w0 (bias):", theta_manual[0])
print("w1~w4:", theta_manual[1:])
print("最终损失:", loss_manual[-1])
# 画损失曲线
plt.plot(loss_manual)
plt.title("手动批量梯度下降损失曲线")
plt.xlabel("迭代次数")
plt.ylabel("MSE Loss")
plt.show()
sample = X_b[0] # 取第一个样本 (含偏置列)
prediction = sample.dot(theta_manual)
print(f"第一个样本预测值: {prediction:.4f} (真实值: {y[0]})")执行结果
python
手动梯度下降结果:
w0 (bias): 0.035957767873506706
w1~w4: [ 2.95579627 0.99249048 2.98615958 -0.98610301]
最终损失: 3.63366540330272e-05
第一个样本预测值: 2.0057 (真实值: 2)2.sklearn框架实现
python
import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans'] # 中文支持
plt.rcParams['axes.unicode_minus'] = False
# ======================
# 1. 数据准备(和你手算的完全一样)
# ======================
X = np.array([
[1, 0, 0, 1],
[0, 2, 1, 0],
[1, 1, 1, 1],
[0, 1, 2, 0],
[1, 0, 1, 2]
])
y = np.array([2, 5, 6, 7, 4])
# 特征标准化(SGD 对尺度敏感,强烈推荐)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# ======================
# 2. 用 sklearn SGDRegressor 模拟全批量梯度下降(BGD)
# ======================
# 初始化 SGDRegressor,设置成"全批量"风格
# 创建模型类
bgd = SGDRegressor(
loss='squared_error', # MSE 损失
penalty=None, # 无正则化(和手动一致)
learning_rate='constant', # 固定学习率
eta0=0.1, # 学习率(和手动一致)
max_iter=1, # 每次 partial_fit 只迭代 1 次
warm_start=True, # 保持之前参数,继续训练
tol=None, # 不使用默认 tol,改用手动控制
random_state=42 # 可复现
)
# 记录损失历史
loss_history = []
n_iterations = 2000 # 和手动一致的迭代次数
for i in range(n_iterations):
# 每次用**全批量**数据训练一次(partial_fit 会用全部样本,因为没指定 batch_size)
bgd.partial_fit(X_scaled, y)
# 计算当前损失(和手动一致的 MSE / 2)
y_pred = bgd.predict(X_scaled)
loss = mean_squared_error(y, y_pred) / 2
loss_history.append(loss)
# ======================
# 3. 输出结果
# ======================
print("\n=== sklearn 模拟全批量梯度下降 (BGD) 结果 ===")
print("w0 (intercept):", bgd.intercept_[0])
print("w1~w4:", bgd.coef_)
print("预测值:", bgd.predict(X_scaled))
print("最终损失 (MSE/2):", loss_history[-1])
print(X_scaled[0], bgd.predict([X_scaled[0]]), y[0])
# ======================
# 4. 画损失曲线(和手动版一样)
# ======================
plt.plot(loss_history)
plt.title("sklearn 模拟全批量梯度下降损失曲线")
plt.xlabel("迭代次数")
plt.ylabel("MSE Loss (除以2)")
plt.grid(True)
plt.show()执行结果
python
=== sklearn 模拟全批量梯度下降 (BGD) 结果 ===
w0 (intercept): 4.800000000000001
w1~w4: [ 1.46969385 0.74833148 1.8973666 -0.74833148]
预测值: [2. 5. 6. 7. 4.]
最终损失 (MSE/2): 1.203012880462043e-30
[ 0.81649658 -1.06904497 -1.58113883 0.26726124] [2.] 2参数不同是因为使用了标准化,当进行预测时,数据也要标准化。与没有使用标准化的计算会成一定比例。