模式识别与机器学习复习笔记（中）

序

本文是国科大《模式识别与机器学习》课程的简要复习，基于课件然后让ai帮忙补充了一些解释。本文是第五到第八章。本文章更多是对于课件的知识点的记录总结，找了点例题和讲解，建议结合其他资料或者课件来看。

第五章 统计机器学习基础

5.1 统计学习根源

什么是机器学习？

机器学习是计算机科学子领域，从模式识别和计算学习理论演化而来。它研究构建能从数据学习并预测的算法，通过示例输入构建模型，进行数据驱动预测，而非静态指令。Arthur Samuel (1959) 定义为"让计算机无需显式编程即可学习"。Tom M. Mitchell定义为：程序从经验E中学习任务T，性能P改善（PAC理论）。

学习任务例子 ：改善任务T的性能P基于经验E。

例如：

T: 垃圾邮件分类，P: 正确分类百分比，E: 标注邮件集合。

T: 手写字识别，P: 正确识别百分比，E: 标注手写字。

T: 下跳棋，P: 赢得概率，E: 多盘游戏经验。

机器学习特点 ：

数据大量廉价、知识稀少；数据过程未知但非随机；通过模式学习模型，反推生成路径；模型是近似（George Box: "All models are wrong, but some are useful"）；模型描述知识或预测；科学本质是模型拟合数据。

机器学习方法分类 ：

有监督学习：有标记数据，e.g., Fisher、感知器、线性判别分析。

无监督学习：无标注数据，e.g., 降维KL变换。

半监督学习：有/无标注混合。

多任务学习：共享相关任务表征。

迁移学习：训练/测试不同分布。

强化学习：间接标注（状态+reward）。

主动学习：主动选择训练数据。

自监督学习：从无标注数据提取监督信号。

5.2 经验风险与期望风险

统计机器学习的目标是：

给定独立同分布（i.i.d.）的训练样本集
{(x1,y1),(x2,y2),...,(xN,yN)}∼p(x,y)\{(\mathbf{x}^1, y^1), (\mathbf{x}^2, y^2), \dots, (\mathbf{x}^N, y^N)\} \sim p(\mathbf{x}, y){(x1,y1),(x2,y2),...,(xN,yN)}∼p(x,y)

我们希望从一个假设空间（函数类）F\mathcal{F}F中找到一个函数f:x↦yf: \mathbf{x} \mapsto yf:x↦y，使得它在所有可能的数据（包括未来未见数据）上表现最好。

这里的关键是：我们永远不知道真实的数据联合分布p(x,y)p(\mathbf{x}, y)p(x,y)，只能通过有限样本去估计。

期望风险（Expected Risk）------理论上的最优目标
定义：

对一个预测函数fff，它的期望风险（也叫真实风险、真风险）定义为
R(f)=E(x,y)∼p(x,y)L(f(x),y)=∫L(f(x),y) p(x,y) dxdyR(f) = \mathbb{E}_{(x,y)\sim p(x,y)} L(f(\\mathbf{x}), y) = \int L(f(\mathbf{x}), y) \, p(\mathbf{x}, y) \, d\mathbf{x} dyR(f)=E(x,y)∼p(x,y)L(f(x),y)=∫L(f(x),y)p(x,y)dxdy

其中：

L(⋅,⋅)L(\cdot, \cdot)L(⋅,⋅) 是损失函数（loss function），衡量预测值f(x)f(\mathbf{x})f(x)和真实标签yyy的差距。

期望是对未知的真实分布p(x,y)p(\mathbf{x}, y)p(x,y)取的。

直观理解：

期望风险就是"在整个宇宙所有可能出现的数据上，平均犯错多少"。这是我们真正关心的指标------泛化能力。

但问题在于：p(x,y)p(\mathbf{x}, y)p(x,y)未知，所以R(f)R(f)R(f)无法直接计算。我们只能用训练数据去"估计"它。

经验风险（Empirical Risk）------我们能直接计算的东西

定义：

用训练样本上的平均损失来估计期望风险，称为经验风险（也叫训练误差、经验误差）：
R^(f)=1N∑i=1NL(f(xi),yi)\hat{R}(f) = \frac{1}{N} \sum_{i=1}^N L(f(\mathbf{x}^i), y^i)R^(f)=N1∑i=1NL(f(xi),yi)

直观理解：

经验风险就是"在已有的N个训练样本上，平均犯错多少"。这是我们能直接算出来的。

经验风险最小化（ERM）原则------最直观的策略

最朴素的想法是：既然R(f)R(f)R(f)算不了，就找一个fff让R^(f)\hat{R}(f)R^(f)最小，这个原则叫经验风险最小化（Empirical Risk Minimization, ERM）。

很多经典算法都是ERM的体现：

最小二乘线性回归 → 最小化训练样本上的平方损失
感知器、SVM（硬间隔） → 最小化训练样本上的误分类数或hinge损失
逻辑回归 → 最小化训练样本上的交叉熵

问题来了：

当模型复杂度很高（假设空间F\mathcal{F}F很大）时，很容易找到一个fff让R^(f)=0\hat{R}(f) = 0R^(f)=0（训练误差为0），但在未知数据上表现很差------这就是过拟合。

回归问题下的最优函数推导

假设回归任务，损失函数为平方损失：
L(f(x),y)=(f(x)−y)2L(f(\mathbf{x}), y) = (f(\mathbf{x}) - y)^2L(f(x),y)=(f(x)−y)2

期望风险：
R(f)=E(f(x)−y)2R(f) = \mathbb{E}(f(\\mathbf{x}) - y)\^2R(f)=E(f(x)−y)2

我们把期望拆开（对固定x\mathbf{x}x条件期望）：
R(f)=ExEy\[(f(x)−y)2∣x]R(f) = \mathbb{E}_\mathbf{x} \left \\mathbb{E}_y \\left\[ (f(\\mathbf{x}) - y)\^2 \\mid \\mathbf{x} \\right \right]R(f)=ExEy\[(f(x)−y)2∣x]

对内层期望展开：
Ey(f(x)−y)2∣x=Ey(f(x)−E\[y∣x+Ey∣x−y)2∣x]\mathbb{E}_y (f(\\mathbf{x}) - y)\^2 \\mid \\mathbf{x} = \mathbb{E}_y (f(\\mathbf{x}) - \\mathbb{E}\[y\|\\mathbf{x} + \mathbb{E}y\|\\mathbf{x} - y)^2 \mid \mathbf{x}]Ey(f(x)−y)2∣x=Ey(f(x)−E\[y∣x+Ey∣x−y)2∣x]
=(f(x)−Ey∣x)2+Ey(y−E\[y∣x)2∣x]= (f(\mathbf{x}) - \mathbb{E}y\|\\mathbf{x})^2 + \mathbb{E}_y (y - \\mathbb{E}\[y\|\\mathbf{x})^2 \mid \mathbf{x}]=(f(x)−Ey∣x)2+Ey(y−E\[y∣x)2∣x]
=(f(x)−Ey∣x)2+Var(y∣x)= (f(\mathbf{x}) - \mathbb{E}y\|\\mathbf{x})^2 + \mathrm{Var}(y|\mathbf{x})=(f(x)−Ey∣x)2+Var(y∣x)

其中第二项是噪声方差（不可约误差），与fff无关。

因此，
R(f)=Ex(f(x)−E\[y∣x)2]+ExVar(y∣x)R(f) = \mathbb{E}\mathbf{x} (f(\\mathbf{x}) - \\mathbb{E}\[y\|\\mathbf{x})^2] + \mathbb{E}\mathbf{x} \\mathrm{Var}(y\|\\mathbf{x})R(f)=Ex(f(x)−E\[y∣x)2]+ExVar(y∣x)

要最小化R(f)R(f)R(f)，只需让
f∗(x)=Ey∣xf^*(\mathbf{x}) = \mathbb{E}y \\mid \\mathbf{x}f∗(x)=Ey∣x

结论：回归问题的最优预测函数就是yyy在给定x\mathbf{x}x下的条件均值。

分类问题下的最优函数推导

假设分类任务，使用0-1损失：
L(f(x),y)=I{f(x)≠y}L(f(\mathbf{x}), y) = \mathbb{I}\{f(\mathbf{x}) \neq y\}L(f(x),y)=I{f(x)=y}

期望风险：
R(f)=EI{f(x)≠y}=P(f(x)≠y)R(f) = \mathbb{E}\\mathbb{I}\\{f(\\mathbf{x}) \\neq y\\} = P(f(\mathbf{x}) \neq y)R(f)=EI{f(x)=y}=P(f(x)=y)

对固定x\mathbf{x}x，误分类概率为：
P(f(x)≠y∣x)=∑kP(y=k∣x)⋅I{f(x)≠k}P(f(\mathbf{x}) \neq y \mid \mathbf{x}) = \sum_{k} P(y=k \mid \mathbf{x}) \cdot \mathbb{I}\{f(\mathbf{x}) \neq k\}P(f(x)=y∣x)=k∑P(y=k∣x)⋅I{f(x)=k}

要最小化误分类概率，只需选择后验概率最大的类别：
f∗(x)=arg⁡max⁡kP(y=k∣x)f^*(\mathbf{x}) = \arg\max_k P(y=k \mid \mathbf{x})f∗(x)=argkmaxP(y=k∣x)

这就是著名的Bayes最优分类器。

对于二分类，若P(y=1∣x)>0.5P(y=1 \mid \mathbf{x}) > 0.5P(y=1∣x)>0.5则判为1，否则判为0（等价于比较P(y=1∣x)P(y=1 \mid \mathbf{x})P(y=1∣x)和P(y=0∣x)P(y=0 \mid \mathbf{x})P(y=0∣x)）。

注意：Bayes分类器是理论上错误率最低的分类器，但实际中后验概率P(y∣x)P(y \mid \mathbf{x})P(y∣x)未知，需要用数据估计。

总结一下：

当N→∞N \to \inftyN→∞时，根据大数定理，R^(f)→R(f)\hat{R}(f) \to R(f)R^(f)→R(f)（对固定的fff）。

但实际NNN有限，且我们要在F\mathcal{F}F中选fff让R^(f)\hat{R}(f)R^(f)最小，这时R^(f)\hat{R}(f)R^(f)可能严重低估R(f)R(f)R(f)（过拟合）。

回归最优：条件均值 f(x)=Ey∣xf(\mathbf{x}) = \mathbb{E}y \\mid \\mathbf{x}f(x)=Ey∣x

分类最优：后验概率最大类 f(x)=arg⁡max⁡P(y∣x)f(\mathbf{x}) = \arg\max P(y \mid \mathbf{x})f(x)=argmaxP(y∣x)

5.3 测试误差估计

我们怎么知道学到的模型在未来未知数据上会表现怎么样？

训练误差（经验风险）很容易算，但它往往会"骗人"（过拟合时训练误差很小，但真实表现差）。所以我们需要用独立于训练过程的数据来估计模型的泛化误差（即期望风险的近似），这就是"测试误差估计"的意义。

为什么需要测试误差估计？

训练误差R^(f)=1Ntrain∑L(f(xi),yi)\hat{R}(f) = \frac{1}{N_{\text{train}}} \sum L(f(\mathbf{x}_i), y_i)R^(f)=Ntrain1∑L(f(xi),yi) 总是乐观的，尤其模型复杂时容易降到0。

我们真正关心的是期望风险R(f)R(f)R(f)，但它算不了。

解决办法：拿出一部分没参与训练的数据（测试集），在上面计算平均损失，作为R(f)R(f)R(f)的无偏估计。这就是测试误差：
etest=1Ntest∑i∈testL(f(xi),yi)e_{\text{test}} = \frac{1}{N_{\text{test}}} \sum_{i \in \text{test}} L(f(\mathbf{x}_i), y_i)etest=Ntest1i∈test∑L(f(xi),yi)

---

5.4 正则化方法 (Regularization)

核心思想：惩罚"任性"的模型

在统计学习中，如果模型为了追求训练误差（经验风险）为 ，会变得极其复杂（比如权重 变得巨大，或者曲线变得极其扭曲），这就会导致过拟合。

正则化 的本质就是：在损失函数后面加一个"紧箍咒"（惩罚项），告诉模型："你可以拟合数据，但你的参数不能太离谱。"

ERM vs SRM

维度	ERM (经验风险最小化)	SRM (结构风险最小化)
目标函数	min⁡R^(f)\min \hat{R}(f)minR^(f)	min⁡R^(f)+λJ(f)\min \hat{R}(f) + \lambda J(f)minR^(f)+λJ(f)
核心逻辑	只要训练集表现好就行。	训练集要好，模型还要简单。
打分机制	只看准确率。	准确率 - 复杂度惩罚。
潜在风险	过拟合（死记硬背噪声）。	欠拟合（如果 过大）。

上表中R^(f)\hat{R}(f)R^(f)是经验风险 (Empirical Risk)，J(f)J(f)J(f)是正则化项 / 惩罚项 (Regularization Term)。

常见的形式：

L2 范数：J(f)=∥w∥2J(f) = \|w\|^2J(f)=∥w∥2。它希望参数 www 都尽量小，分布均匀，不要出现某些特别巨大的权重。

L1 范数：J(f)=∥w∥1J(f) = \|w\|_1J(f)=∥w∥1。它希望参数尽量稀疏，不重要的特征权重直接减为 0。

【直观理解】

• ERM 像是一个拼命刷题的考生，背下了卷子上所有的干扰项（噪声），遇到新题就傻眼了。
• SRM 像是一个寻找规律的考生，他宁愿放弃几个奇怪的特例（牺牲一点训练精度），也要总结出简单的通用公式。
• λ\lambdaλ（超参数）：它是你的"容忍度"。 越大，你对模型复杂度的容忍度越低，模型越倾向于平滑、简单。

---

三大主流正则化工具

(1) L2 正则：岭回归 (Ridge) ------ "集体瘦身"

• 数学形式 ：J(f)=∥w∥22=∑wj2J(f) = \| \mathbf{w} \|^2_2 = \sum w_j^2J(f)=∥w∥22=∑wj2
• 效果：惩罚权重的平方。它让每个 都变小，趋近于 ，但很难真正等于 。
• 【直观理解】：它像是一股向心力，把原本张牙舞爪的权重向量 整体拉向原点。由于平方项的存在，权重越大惩罚越重，所以它最讨厌"一枝独秀"的大权重，更喜欢"平庸"的小权重集合。
• 贝叶斯解释 ：假设参数 服从高斯分布。

(2) L1 正则：Lasso ------ "优胜劣汰"

• 数学形式 ：J(f)=∥w∥1=∑∣wj∣J(f) = \| \mathbf{w} \|_1 = \sum |w_j|J(f)=∥w∥1=∑∣wj∣
• 效果 ：惩罚权重的绝对值。它会产生稀疏解，即把很多不重要的特征权重直接压成 。
• 【直观理解】：L1 正则非常"狠"，它不仅让权重变小，还会直接"劝退"那些贡献不大的特征。
• 几何解释：L1 的等值线是"带尖角的菱形"，而损失函数的等值线更有可能在尖角处（坐标轴上）与之相碰，此时某个坐标轴的值即为 。
• 贝叶斯解释 ：假设参数 服从拉普拉斯分布。

(3) 弹性网络 (Elastic Net) ------ "中庸之道"

• 数学形式 ：λρ∥w∥1+(1−ρ)∥w∥22\lambda \\rho \\\| \\mathbf{w} \\\|_1 + (1-\\rho) \\\| \\mathbf{w} \\\|_2\^2 λρ∥w∥1+(1−ρ)∥w∥22
• 效果：结合了 L1 的自动特征选择和 L2 的稳定性。
• 适用场景 ：当你有多个高度相关的特征时，Lasso 可能会随机选一个，而 Elastic Net 会倾向于把它们一起保留或剔除。

---

偏差-方差权衡 (Bias-Variance Tradeoff)

正则化本质上是在做一场交易：用增加偏差（Bias）的代价，来大幅降低方差（Variance）。

• 无正则化 () ：模型完全拟合数据。低偏差 （训练得准），但高方差（换个数据集结果全变了）。
• 强正则化 () ：模型变得极简（如变成一条水平线）。高偏差 （训练得不准），但低方差（非常稳定，换什么数据都长这样）。

结论 ：正则化的艺术就在于通过交叉验证找到那个 ，使得总误差 = 偏差² + 方差 + 噪声 达到最小。

5.5 泛化理论与 VC 维

泛化误差界 (Generalization Error Bound)

我们真正关心的是模型在全样本空间上的期望风险 R(f)R(f)R(f)，但我们只能观测到经验风险 R^(f)\hat{R}(f)R^(f)。泛化理论给出了两者的关系：
R(f)≤R^(f)+ϵ(N,H,δ)R(f) \leq \hat{R}(f) + \epsilon(N, \mathcal{H}, \delta)R(f)≤R^(f)+ϵ(N,H,δ)
ϵ\epsilonϵ（泛化误差界）：即"惩罚项"，它代表了模型从训练集迁移到测试集时的"信心不足程度"。

影响因素：

1. 样本量 NNN：NNN 越大，ϵ\epsilonϵ 越小（见多识广，预测越准）。
2. 模型容量 H\mathcal{H}H：模型空间越复杂，ϵ\epsilonϵ 越大（越容易瞎猜，风险越高）。

VC 维：衡量模型能力的尺子

如何量化"模型有多复杂"？除了参数个数，统计学习引入了 VC 维 (Vapnik-Chervonenkis Dimension)。

核心概念：打散 (Shattering)

定义 ：如果一个模型空间 H\mathcal{H}H 能够实现 NNN 个点在所有可能的 2N2^N2N 种标签组合下的正确分类，就称这 NNN 个点能被该模型空间打散。
VC 维定义 ：模型空间 H\mathcal{H}H 能够打散的最大样本集的大小。

【直观理解】

想象你在玩一个"连点成线"的游戏。

• D=1（线性模型在1维）：给定2个点，无论标签是 (0,0), (1,1), (1,0), (0,1)，你都能用一个点（阈值）把它们分开。但如果是3个点（如两头是0，中间是1），直线就没辙了。所以 D=1 的线性模型 VC 维是 2。
• D=2（平面上的直线）：能打散任意 3 个点，但无法打散 4 个点（如 XOR 异或布局）。因此，平面直线的 VC 维是 3。
• 结论 ：通常情况下，线性模型的 VC 维 ≈\approx≈ 参数个数 + 1。

---

为什么引入 VC 维？（深层逻辑）

VC 维给出了泛化误差的具体上限。对于一个 VC 维为 的模型，当样本量 足够大时，泛化误差界满足：
ϵ∝dln⁡(N/d)+ln⁡(1/δ)N\epsilon \propto \sqrt{\frac{d \ln(N/d) + \ln(1/\delta)}{N}}ϵ∝Ndln(N/d)+ln(1/δ)

这个公式非常有启发性，它告诉我们：

1. 模型越强（ddd 越大）：虽然训练误差 R^(f)\hat{R}(f)R^(f) 会下降，但右边的误差界 ϵ\epsilonϵ 会迅速膨胀。
2. 数据越多（NNN 越大）：误差界 ϵ\epsilonϵ 会收敛到 0，此时经验风险就等于期望风险。

总结：正则化、VC 维与结构风险最小化 (SRM)

现在我们可以把这些概念串联起来了：

1. 正则化 中的 J(f)J(f)J(f)，本质上就是在工程上限制模型的 VC 维。
2. VC 维 是在理论上度量 J(f)J(f)J(f) 所代表的复杂度。
3. SRM (结构风险最小化) 准则就是要求我们在训练时，同时考虑"训练得准不准"（经验风险）和"模型强不强"（VC 维引起的泛化风险）。

第六章 有监督学习方法

6.1 有监督学习概览

有监督学习的目标是利用带标记的训练集，学习一个能对未知样本进行预测的推断函数。

核心模型分类

• 判别式模型 (Discriminative)

• 方法 ：直接对条件概率 P(y∣x)P(y|x)P(y∣x) 或判别函数 f(x)f(x)f(x) 建模。

• 直观理解：它直接学习"分类边界"。看到一个样本，它直接告诉你这个点在边界的哪一侧。

• 典型算法：线性回归、逻辑回归、SVM、神经网络。

• 生成式模型 (Generative)

• 方法 ：先学习联合分布 P(x,y)P(x,y)P(x,y)，再通过贝叶斯定理计算后验概率 P(y∣x)P(y|x)P(y∣x)。

• 直观理解：它学习每一类数据的"长相"。看到一个样本，它会对比这个样本更像哪一类的分布。

• 典型算法：朴素贝叶斯、高斯判别分析 (GDA)。

6.2 线性回归与最小二乘法 (LMS)

问题定义

给定 NNN 个样本 (xi,yi)(x^i, y^i)(xi,yi)，目标是找到权重向量 www，使得预测值 f(x)=wTxf(x) = w^T xf(x)=wTx 与真实值 yyy 的差距最小。

损失函数（L2 损失）：

J(w)=∑i=1N(wTxi−yi)2=∥Xw−y∥2J(w) = \sum_{i=1}^N (w^T x^i - y^i)^2 = \|Xw - y\|^2J(w)=i=1∑N(wTxi−yi)2=∥Xw−y∥2

求解方案

方案 A：解析解（正规方程）

通过求导并令导数为 0，直接得出最优解：

w∗=(XTX)−1XTyw^* = (X^T X)^{-1} X^T yw∗=(XTX)−1XTy

【几何视角】

在特征空间中，预测值 y^=Xw\hat{y} = Xwy^=Xw 是真实观测值 yyy 在特征矩阵 XXX 的列空间上的正交投影。正交意味着误差向量 (y−y^)(y - \hat{y})(y−y^) 与特征空间垂直，此时误差平方和达到最小值。

方案 B：梯度下降（迭代更新）

当数据量巨大（矩阵求逆太慢）时，采用迭代法：

wnew=wold−α∇J(w)w_{new} = w_{old} - \alpha \nabla J(w)wnew=wold−α∇J(w)

• 批梯度下降 (BGD) ：每次更新使用全量数据。收敛平滑，但数据量大时计算极慢。
• 随机梯度下降 (SGD) ：每次只用一个样本。速度快，能处理流式数据，但收敛路径是震荡的。

---

6.3 概率视角下的回归

为什么用平方误差？（MLE 解释）

如果我们假设观测值 yyy 是由真实线性关系加上高斯噪声 ϵ∼N(0,σ2)\epsilon \sim \mathcal{N}(0, \sigma^2)ϵ∼N(0,σ2) 构成的，那么：

最大似然估计 (MLE) 等价于 最小二乘法 (LMS)。

这说明最小二乘法背后的假设是误差呈正态分布。

为什么加正则化？（MAP 解释）

在极大似然估计的基础上，如果我们假设权重 www 本身也服从某种分布（先验）：

1. 高斯先验   ⟹  \implies⟹ 推导结果等价于 L2 正则化 (Ridge)。
2. 拉普拉斯先验   ⟹  \implies⟹ 推导结果等价于 L1 正则化 (Lasso)。

6.4 鲁棒性与进阶优化

1. 应对异常值：Huber 损失痛点：L2 损失由于有平方项，会极大放大异常值（Outlier）的误差，导致模型被带偏。解决：Huber 损失在误差较小时使用平方（L2），误差较大时切换为线性（L1），从而对异常值更具鲁棒性。
2. 应对不可导点：次梯度 (Subgradient)L1 正则化在 w=0w=0w=0 处是个尖角，无法求导。方法：使用次梯度，即在尖点处任选一个位于其梯度包络范围内的值作为下降方向。

6.5 逻辑回归 (Logistic Regression)

虽然名字叫"回归"，但它是不折不扣的分类模型 。它的核心逻辑是：在线性回归的基础上，套一个"壳子"，把连续的预测值映射到 (0,1)(0, 1)(0,1) 区间，表示概率。

Sigmoid 函数：非线性的桥梁

g(z)=11+e−zg(z) = \frac{1}{1 + e^{-z}}g(z)=1+e−z1

作用：将实数域的输出 z=wTxz = w^T xz=wTx 压缩到 (0,1)(0, 1)(0,1)。

模型假设：hw(x)=g(wTx)=P(y=1∣x;w)h_w(x) = g(w^T x) = P(y=1 \mid x; w)hw(x)=g(wTx)=P(y=1∣x;w)。

对数几率 (Logit) 的直观理解

如果我们把公式变形：
ln⁡P(y=1∣x)P(y=0∣x)=wTx\ln \frac{P(y=1 \mid x)}{P(y=0 \mid x)} = w^T xlnP(y=0∣x)P(y=1∣x)=wTx

左边：称为"对数几率"（Log-odds）。

物理意义：逻辑回归本质上是在用线性回归去拟合样本属于正类的相对可能性。

参数估计：极大似然估计 (MLE)

不同于线性回归用平方损失，逻辑回归使用交叉熵损失 (Cross-Entropy Loss)：

似然函数：L(w)=∏hw(xi)yi1−hw(xi)1−yiL(w) = \prod h_w(x\^i)^{y^i} 1 - h_w(x\^i)^{1-y^i}L(w)=∏hw(xi)yi1−hw(xi)1−yi

对数损失：J(w)=−∑yiln⁡hw(xi)+(1−yi)ln⁡(1−hw(xi))J(w) = -\sum y\^i \\ln h_w(x\^i) + (1-y\^i) \\ln(1 - h_w(x\^i))J(w)=−∑yilnhw(xi)+(1−yi)ln(1−hw(xi))

优化：该函数是凸函数，使用梯度下降更新：w←w+α∑(yi−hw(xi))xiw \leftarrow w + \alpha \sum (y^i - h_w(x^i))x^iw←w+α∑(yi−hw(xi))xi。

• 注意：更新公式的形式和线性回归相似。

6.6 从二分类到多分类：Softmax 回归

当类别数 K>2K > 2K>2 时，逻辑回归进化为 Softmax 回归。

核心公式：对每一类 kkk 计算一个得分 zkz_kzk，然后归一化：P(y=k∣x)=ewkTx∑j=1KewjTxP(y=k \mid x) = \frac{e^{w_k^T x}}{\sum_{j=1}^K e^{w_j^T x}}P(y=k∣x)=∑j=1KewjTxewkTx

特点：所有类别的概率之和等于 1。

决策规则：选概率最大的那一类。

6.7 生成式分类器：高斯判别分析 (GDA)

逻辑回归是直接求 P(y∣x)P(y|x)P(y∣x)（判别式），而 GDA 走的是"先建模分布，再用贝叶斯推导"的路线（生成式）。

模型假设

先验：y∼Bernoulli(ϕ)y \sim \text{Bernoulli}(\phi)y∼Bernoulli(ϕ)

类条件概率（关键）：假设每一类数据都服从高斯分布：
x∣y=0∼N(μ0,Σ)x \mid y=0 \sim \mathcal{N}(\mu_0, \Sigma)x∣y=0∼N(μ0,Σ)
x∣y=1∼N(μ1,Σ)x \mid y=1 \sim \mathcal{N}(\mu_1, \Sigma)x∣y=1∼N(μ1,Σ)

注意：通常假设各类别协方差矩阵 Σ\SigmaΣ 相同。

通过贝叶斯公式推导后可以发现，如果协方差矩阵 Σ\SigmaΣ 相同，GDA 的后验概率 P(y∣x)P(y|x)P(y∣x) 形式上也是一个 Sigmoid 函数，且决策边界是线性的。

决策边界

通过贝叶斯公式推导后可以发现，如果协方差矩阵 Σ\SigmaΣ 相同，GDA 的后验概率 P(y∣x)P(y|x)P(y∣x) 形式上也是一个 Sigmoid 函数，且决策边界是线性的。

6.8 逻辑回归 vs. GDA

1. 假设强弱：

• GDA 假设很强（数据必须是高斯分布）。如果假设正确，GDA 只需要更少的数据就能学得很好（训练效率高）。
• 逻辑回归 假设很弱。它更具鲁棒性 (Robust)，即使数据不是高斯分布（比如是泊松分布），它依然能工作得很好。

2. 数据量：

• 数据量小时，GDA 往往表现更好（因为先验假设起了引导作用）。
• 数据量大时，逻辑回归通常更优，因为它能根据数据自适应调整。

6.9 感知机算法 (Perceptron)

感知机是最古老的分类算法之一，也是神经网络的基石。

• 模型 ：y=sgn(wTx+b)y = \text{sgn}(w^T x + b)y=sgn(wTx+b)。

• 损失函数：误分类点到超平面的总距离。

• 更新准则 ：只要分类错了，就进行更新：
  w←w+αyixiw \leftarrow w + \alpha y^i x^iw←w+αyixi

• 局限性 ：只能处理线性可分的数据。如果数据不是线性可分的，感知机永远不会收敛（会一直震荡）。

---

6.10 非平衡数据集处理 (Imbalanced Learning)

在现实中，负样本往往远多于正样本（例如 99.9% 的交易是正常的）。此时模型如果全猜负类，准确率高达 99.9%，但毫无意义。

1. 采样方法 (Sampling)

• 欠采样 (Under-sampling)：随机丢弃一些大类样本。优点是快，缺点是可能丢失重要信息。
• 过采样 (Over-sampling) ：复制小类样本，或者通过 SMOTE 算法在小类样本之间"插值"生成新样本。

2. 代价敏感学习 (Cost-Sensitive Learning)

• 核心思想：既然正样本稀少且重要，我们就人为提高它分类错误的"代价"。
• 损失函数改造：给损失函数加权重。

J(w)=∑i∈positiveCposL(f,y)+∑i∈negativeCnegL(f,y)J(w) = \sum_{i \in \text{positive}} C_{pos} L(f, y) + \sum_{i \in \text{negative}} C_{neg} L(f, y)J(w)=i∈positive∑CposL(f,y)+i∈negative∑CnegL(f,y)其中让 Cpos>CnegC_{pos} > C_{neg}Cpos>Cneg。

---

6.11 模型评估指标：超越准确率

当数据不平衡时，准确率 (Accuracy) 会失效，我们需要更精细的尺子。

1. 混淆矩阵 (Confusion Matrix)

• 真正例 (TP)：真阳性。
• 假正例 (FP)：误报（把好人当坏人）。
• 假负例 (FN)：漏报（把坏人放走了）。

2. 精确率 (Precision) vs. 召回率 (Recall)

精确率P ：TP/(TP+FP)TP / (TP + FP)TP/(TP+FP)。预测为正的里面，有多少是真的？（强调"抓得准"）。

召回率R：TP/(TP+FN)TP / (TP + FN)TP/(TP+FN)。所有的正类里面，抓到了多少？（强调"抓得全"）。

F1-score：两者的调和平均，用于综合评价。

3. ROC 曲线与 AUC 值 (核心考点)

• ROC 曲线：横轴是假正类率 (FPR)，纵轴是真正类率 (TPR)。通过调节分类阈值（从 0 到 1），画出的一条曲线。
• AUC (Area Under Curve)：ROC 曲线下的面积。
• 直观物理意义 ：随机取一个正样本和一个负样本，模型给正样本打分高于负样本的分数的概率。
• 性质：AUC 越接近 1，模型排序能力越强；AUC = 0.5 等于随机瞎猜。

---

6.12 概率校准 (Probability Calibration)

有时候模型给出的"概率"并不是真实的频率（例如逻辑回归倾向于给出极端的 0 或 1）。

• Platt Scaling：在原始输出上再套一个逻辑回归。
• Isotonic Regression：一种非参数的校准方法。

6.13 名词术语记录

针对下面的术语，可以检测一下哪个术语还不理解，不理解的查一下，后面还会用到。

有监督学习、判别式模型、生成式模型、极大似然估计 (MLE)、最大后验估计 (MAP)、贝叶斯定理、结构风险最小化 (SRM)、最小二乘法 (LMS/OLS)、残差、正规方程、梯度下降、随机梯度下降 (SGD)、批梯度下降 (BGD)、学习率、L2正则化、岭回归 (Ridge)、L1正则化、Lasso、次梯度、Huber损失、逻辑回归、对数几率 (Logit)、Sigmoid函数、Softmax回归、交叉熵损失、高斯判别分析 (GDA)、感知机、线性可分、混淆矩阵、真正例 (TP)、假正例 (FP)、真负例 (TN)、假负例 (FN)、精确率 (Precision)、召回率 (Recall)、F1分数、ROC曲线、AUC值、欠采样、过采样、SMOTE算法、代价敏感学习、概率校准

第七章：支持向量机 (Support Vector Machine, SVM)

这一章SVM是模式识别的核心算法之一，它不像Logistic回归那样追求概率，而是直接找"最稳"的分界线。SVM的核心是最大化间隔。

7.1 间隔 (Margin) 与分类置信度

SVM从Logistic回归的置信度概念出发，但引入几何距离作为更可靠的"信心"指标。

在Logistic回归中，置信度通过Sigmoid函数定义：

P(y=1∣x)=11+e−wTx P(y=1|x) = \frac{1}{1+e^{-w^T x}} P(y=1∣x)=1+e−wTx1

• 推导动机 ：wTxw^T xwTx 越大，表示样本越远离决策边界，分类越自信。但这只是概率视角，SVM问：除了概率，怎么量化"远离"？

SVM用点到超平面的距离作为置信度。在特征空间中，样本是点，决策边界是超平面，距离反映了"安全缓冲"。

细节要点

• 二分类问题：样本 (x,y),y∈{−1,1}(x, y), y \in \{-1, 1\}(x,y),y∈{−1,1}。
• 线性分类器：fw,b(x)=g(wTx+b)f_{w,b}(x) = g(w^T x + b)fw,b(x)=g(wTx+b)，其中 g(z)=1g(z) = 1g(z)=1 如果 z≥0z \ge 0z≥0，否则 −1-1−1。
• 超平面：wTx+b=0w^T x + b = 0wTx+b=0。

【直观理解】：想象垃圾邮件分类，绿色点是Ham（正常邮件），红色点是Spam（垃圾）。决策线像"防火墙"，点离墙越远，越自信不会"越界"。这比Logistic的"软概率"更"硬核"，像找一条街把两帮人分开，还留出最大缓冲区避免打架。

补充：课件用Ham/Spam例子展示了多条可能线，但SVM选"最中间"那条------这预示了最大间隔。

---

7.2 函数间隔 (Functional Margin) 与几何间隔 (Geometric Margin)

函数间隔

对于样本 (xi,yi)(x^i, y^i)(xi,yi)，函数间隔 γ^i=yi(wTxi+b)\hat{\gamma}^i = y^i (w^T x^i + b)γ^i=yi(wTxi+b)。

• 数据集整体：γ^=min⁡iγ^i\hat{\gamma} = \min_i \hat{\gamma}^iγ^=miniγ^i。

推导动机 ：为什么这样定义？因为yiy^iyi确保正负类同向：正类要wTxi+b≫0w^T x^i + b \gg 0wTxi+b≫0，负类≪0\ll 0≪0。大正值表示"正确且自信"。

变量解释：

• yiy^iyi：标签（1或-1）。
• wTxi+bw^T x^i + bwTxi+b：线性投影值。
• γ^i>0\hat{\gamma}^i > 0γ^i>0：正确分类；越大越自信。

几何间隔

几何间隔 γi=yi((w∥w∥2)Txi+b∥w∥2)\gamma^i = y^i \left( \left( \frac{w}{\|w\|_2} \right)^T x^i + \frac{b}{\|w\|_2} \right)γi=yi((∥w∥2w)Txi+∥w∥2b)。

• 数据集整体：γ=min⁡iγi=γ^∥w∥2\gamma = \min_i \gamma^i = \frac{\hat{\gamma}}{\|w\|_2}γ=miniγi=∥w∥2γ^。

推导动机 ：函数间隔会随www缩放而变（e.g., 倍增www，间隔也倍增），不稳定。几何间隔归一化∥w∥2=1\|w\|_2=1∥w∥2=1，获得尺度不变的"真实距离"------像量身高时统一单位。

变量解释：

• ∥w∥2\|w\|_2∥w∥2：权重范数（L2 norm）。
• w∥w∥2\frac{w}{\|w\|_2}∥w∥2w：单位方向向量。
• 如果∥w∥2=1\|w\|_2=1∥w∥2=1，函数与几何间隔相等。

对比表：函数间隔 vs 几何间隔

维度	函数间隔 (Functional Margin)	几何间隔 (Geometric Margin)
学习目标	最大化γ^\hat{\gamma}γ^，但易受www缩放影响	最大化γ\gammaγ，追求泛化能力（VC维界限）
数据效率	适用于线性可分数据，但不鲁棒	更鲁棒，考虑实际距离，适合高维
典型算法	基础线性分类器	SVM核心，结合QP求解
几何解释	投影值的大小	点到平面的欧氏距离

【直观理解】 ：函数间隔像"标尺上的刻度"，但标尺可伸缩；几何间隔像"实际步行距离"，不变。特征空间中，点到线的垂直距离就是γ\gammaγ------SVM要让最近的点也"远走高飞"。

---

7.3 最优间隔分类器 (Optimal Margin Classifier)

线性SVM优化问题（假设线性可分）：

min⁡w,b12∥w∥22 \min_{w, b} \frac{1}{2} \|w\|_2^2 w,bmin21∥w∥22

s.t. yi(wTxi+b)≥1,i=1,...,Ny^i (w^T x^i + b) \geq 1, i=1,\dots,Nyi(wTxi+b)≥1,i=1,...,N。

推导动机 ：最大化γ=1∥w∥2\gamma = \frac{1}{\|w\|_2}γ=∥w∥21 等价于最小化∥w∥22\|w\|_2^2∥w∥22（平方便于求导），约束确保函数间隔γ^=1\hat{\gamma}=1γ^=1。

变量解释：

• 12∥w∥22\frac{1}{2} \|w\|_2^221∥w∥22：正则项，控制模型复杂度。
• 约束：所有点至少间隔1。

输出：分离超平面 w∗Tx+b∗=0w^{*T} x + b^* = 0w∗Tx+b∗=0，判别函数 sign(w∗Tx+b∗)\text{sign}(w^{*T} x + b^*)sign(w∗Tx+b∗)。

【核心思想】 ：像在两军阵前挖最宽的壕沟------壕沟宽度2∥w∥2\frac{2}{\|w\|_2}∥w∥22，支持向量是"壕沟边上的哨兵"。

典型例题 数据：x1=3,3T,y1=1x^1=3,3^T, y^1=1x1=3,3T,y1=1; x2=4,3T,y2=1x^2=4,3^T, y^2=1x2=4,3T,y2=1; x3=1,1T,y3=−1x^3=1,1^T, y^3=-1x3=1,1T,y3=−1。

步骤1：设置约束yi(wTxi+b)≥1y^i (w^T x^i + b) \ge 1yi(wTxi+b)≥1。本题三个约束条件可以写成：

对于 x1x^1x1: 3w1+3w2+b=13w_1 + 3w_2 + b = 13w1+3w2+b=1

对于 x2x^2x2: 4w1+3w2+b≥14w_1 + 3w_2 + b \ge 14w1+3w2+b≥1

对于 x3x^3x3: 1w1+1w2+b=−11w_1 + 1w_2 + b = -11w1+1w2+b=−1

步骤2：目标min⁡12(w12+w22)\min \frac{1}{2} (w_1^2 + w_2^2)min21(w12+w22)。

步骤3：求解得w∗=0.5,0.5T,b∗=−2w^*=0.5,0.5^T, b^*=-2w∗=0.5,0.5T,b∗=−2。

验证：带入x1x^1x1，0.5∗3+0.5∗3−2=1>00.5*3 + 0.5*3 -2=1>00.5∗3+0.5∗3−2=1>0，正确分开。

易混：为什么12\frac{1}{2}21？便于对偶推导时系数简洁。

一些需要注意的点：

点 x1(3,3)x^1(3,3)x1(3,3) 和 x3(1,1)x^3(1,1)x3(1,1) 是两类点中距离最近的"边界点"。它们支撑起了整个分类间隔，因此它们必须处于等号成立的状态。如果它们不取等号，间隔（Margin）就可以进一步扩大，那就不是"最大间隔"了。点 x2(4,3)x^2(4,3)x2(4,3) 是一个正样本，它在 x1x^1x1 的"后方"，也就是更远离分类边界的地方。SVM 的通用约束要求是：yi(wTxi+b)≥1y^i(w^T x^i + b) \ge 1yi(wTxi+b)≥1。对于 x2x^2x2，代入我们算出的结果：0.5(4)+0.5(3)−2=1.50.5(4) + 0.5(3) - 2 = 1.50.5(4)+0.5(3)−2=1.5。显然 1.5>11.5 > 11.5>1，这说明 x2x^2x2 落在间隔边界之外的"安全区"。SVM 是一次"由少数人决定的选举"：只有那两个取等号的支持向量在干活，那个取大于号的样本只是在旁边围观。

在刚才的例题中，只有 3 个样本，手动观察一下就能猜出谁是支持向量，然后列方程组。但如果是在实际应用中，样本量 NNN 极大，同时也无法扩展到高维。所以提出了拉格朗日对偶问题。

转换为拉格朗日对偶问题的主要目的：

1. 方便求解：把复杂的不等式约束转化成较简单的等式约束。
2. 打破维度限制：使 SVM 的复杂度由样本数（支持向量数）决定，而非特征维度决定。
3. 开启非线性大门：没有对偶形式，就无法引入核函数，SVM 就只能处理像你例题中这样简单的线性数据，无法处理复杂的现实问题。

---

7.4 拉格朗日对偶问题 (Lagrange Dual)

一般情形

原问题：min⁡wf(w)\min_w f(w)minwf(w) s.t. gi(w)≤0,hi(w)=0g_i(w) \le 0, h_i(w)=0gi(w)≤0,hi(w)=0。

拉格朗日函数：L(w,α,β)=f(w)+∑αigi+∑βihi,αi≥0L(w,\alpha,\beta) = f(w) + \sum \alpha_i g_i + \sum \beta_i h_i, \alpha_i \ge 0L(w,α,β)=f(w)+∑αigi+∑βihi,αi≥0。

对偶：max⁡α,βmin⁡wL\max_{\alpha,\beta} \min_w Lmaxα,βminwL。

推导动机 ：原问题难解（约束多），对偶转成无约束max-min，凸问题下d∗=p∗d^*=p^*d∗=p∗（强对偶）。

KKT条件：梯度0、互补松弛αi∗gi(w∗)=0\alpha_i^* g_i(w^*)=0αi∗gi(w∗)=0等。

SVM对偶

SVM对偶：

max⁡α∑αi−12∑yiyjαiαj(xi)Txj \max_{\alpha} \sum \alpha_i - \frac{1}{2} \sum y^i y^j \alpha_i \alpha_j (x^i)^T x^j αmax∑αi−21∑yiyjαiαj(xi)Txj

s.t. αi≥0,∑αiyi=0\alpha_i \ge 0, \sum \alpha_i y^i =0αi≥0,∑αiyi=0。

w∗=∑αi∗yixiw^* = \sum \alpha_i^* y^i x^iw∗=∑αi∗yixi。

【直观理解】 ：对偶像"影子戏法"------原问题追www，对偶用α\alphaα（仅支持向量α>0\alpha>0α>0）重构www，计算只剩内积，便于核扩展。几何上，支持向量"支撑"整个平面。

典型例题 ：还是对于上面的例题，这里进行重新计算。

对偶优化：
max⁡α∑i=13αi−12∑i,j=13yiyjαiαj(xi)Txj \max_{\alpha} \sum_{i=1}^{3} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{3} y^i y^j \alpha_i \alpha_j (x^i)^T x^j αmaxi=1∑3αi−21i,j=1∑3yiyjαiαj(xi)Txj

s.t. αi≥0\alpha_i \geq 0αi≥0, ∑i=13αiyi=0\sum_{i=1}^{3} \alpha_i y^i = 0∑i=13αiyi=0。（硬间隔，αi\alpha_iαi 上界无限）

步骤1：计算内积矩阵（Gram矩阵）

(xi)Txj(x^i)^T x^j(xi)Txj：

• x1⋅x1=3∗3+3∗3=18x^1 \cdot x^1 = 3*3 + 3*3 = 18x1⋅x1=3∗3+3∗3=18
• x1⋅x2=3∗4+3∗3=21x^1 \cdot x^2 = 3*4 + 3*3 = 21x1⋅x2=3∗4+3∗3=21
• x1⋅x3=3∗1+3∗1=6x^1 \cdot x^3 = 3*1 + 3*1 = 6x1⋅x3=3∗1+3∗1=6
• x2⋅x2=4∗4+3∗3=25x^2 \cdot x^2 = 4*4 + 3*3 = 25x2⋅x2=4∗4+3∗3=25
• x2⋅x3=4∗1+3∗1=7x^2 \cdot x^3 = 4*1 + 3*1 = 7x2⋅x3=4∗1+3∗1=7
• x3⋅x3=1∗1+1∗1=2x^3 \cdot x^3 = 1*1 + 1*1 = 2x3⋅x3=1∗1+1∗1=2

步骤2：计算二次项系数 yiyj(xi)Txjy^i y^j (x^i)^T x^jyiyj(xi)Txj

矩阵 QQQ（对称）：

	i=1 (y=1)	i=2 (y=1)	i=3 (y=-1)
j=1	1 * 1 * 18=18	1 * 1 * 21=21	1 * (-1) * 6=-6
j=2	21	1 * 1 * 25=25	1*(-1)*7=-7
j=3	-6	-7	(-1)*(-1)*2=2

步骤3：约束 α1+α2−α3=0\alpha_1 + \alpha_2 - \alpha_3 = 0α1+α2−α3=0 （即 α3=α1+α2\alpha_3 = \alpha_1 + \alpha_2α3=α1+α2）

代入目标函数，只剩 α1,α2\alpha_1, \alpha_2α1,α2：

W(α1,α2)=α1+α2+α3−12(αTQα)W(\alpha_1, \alpha_2) = \alpha_1 + \alpha_2 + \alpha_3 - \frac{1}{2} (\alpha^T Q \alpha)W(α1,α2)=α1+α2+α3−21(αTQα)

因为 α3=α1+α2\alpha_3 = \alpha_1 + \alpha_2α3=α1+α2，展开二次项得：

W=α1+α2+(α1+α2)−12(18α12+25α22+2α32+42α1α2−12α1α3−14α2α3)W = \alpha_1 + \alpha_2 + (\alpha_1 + \alpha_2) - \frac{1}{2} (18\alpha_1^2 + 25\alpha_2^2 + 2\alpha_3^2 + 42\alpha_1\alpha_2 -12\alpha_1\alpha_3 -14\alpha_2\alpha_3)W=α1+α2+(α1+α2)−21(18α12+25α22+2α32+42α1α2−12α1α3−14α2α3)

代入 α3\alpha_3α3 并化简：

最终得到：W(α1,α2)=2(α1+α2)−4α12−10α1α2−6.5α22W(\alpha_1, \alpha_2) = 2(\alpha_1 + \alpha_2) - 4\alpha_1^2 - 10\alpha_1\alpha_2 - 6.5\alpha_2^2W(α1,α2)=2(α1+α2)−4α12−10α1α2−6.5α22
步骤4：求导置零

∂W∂α1=0⇒8α1+10α2=1\frac{\partial W}{\partial \alpha_1} = 0\Rightarrow 8\alpha_1 + 10\alpha_2 = 1∂α1∂W=0⇒8α1+10α2=1
∂W∂α2=0⇒10α1+13α2=2\frac{\partial W}{\partial \alpha_2} = 0 \Rightarrow 10\alpha_1 + 13\alpha_2 = 2∂α2∂W=0⇒10α1+13α2=2

解得：α₁ = 1.5, α₂ = -1（无效，因为α ≥ 0）。

临界点在可行域外，说明最大值在边界（α₁=0 或 α₂=0）。

步骤5：边界搜索

（最大化W）

α2=0\alpha_2=0α2=0 时：最优 α1=0.25\alpha_1 = 0.25α1=0.25，α3=0.25\alpha_3=0.25α3=0.25，W=0.25W=0.25W=0.25
α1=0\alpha_1=0α1=0 时：WWW 较小

最优：α∗=0.25,0,0.25\alpha^* = 0.25, 0, 0.25α∗=0.25,0,0.25

步骤6：恢复原参数
w∗=∑αi∗yixi=0.25⋅3,3T−0.25⋅1,1T=0.5,0.5Tw^* = \sum \alpha_i^* y^i x^i = 0.25 \cdot 3,3^T - 0.25 \cdot 1,1^T = 0.5, 0.5^Tw∗=∑αi∗yixi=0.25⋅3,3T−0.25⋅1,1T=0.5,0.5T
∥w∗∥2=0.5≈0.707\|w^*\|_2 = \sqrt{0.5} \approx 0.707∥w∗∥2=0.5 ≈0.707

用支持向量计算b∗b^*b∗（取x1x^1x1）：
y1(w∗Tx1+b∗)=1⇒0.5⋅3+0.5⋅3+b∗=1⇒b∗=−2y^1 (w^{*T} x^1 + b^*) = 1 \Rightarrow 0.5\cdot3 + 0.5\cdot3 + b^* =1 \Rightarrow b^* = -2y1(w∗Tx1+b∗)=1⇒0.5⋅3+0.5⋅3+b∗=1⇒b∗=−2
步骤7：决策函数

分离超平面：0.5x1+0.5x2−2=00.5 x_1 + 0.5 x_2 - 2 = 00.5x1+0.5x2−2=0，即 x1+x2=4x_1 + x_2 = 4x1+x2=4。

判别函数：f(x)=sign(0.5x1+0.5x2−2)f(x) = \text{sign}(0.5 x_1 + 0.5 x_2 - 2)f(x)=sign(0.5x1+0.5x2−2)。

几何间隔：γ=1/∥w∗∥2=2≈1.414\gamma = 1 / \|w^*\|_2 = \sqrt{2} \approx 1.414γ=1/∥w∗∥2=2 ≈1.414。

步骤8：验证分类与约束

x1x^1x1：0.5⋅3+0.5⋅3−2=10.5\cdot3 + 0.5\cdot3 -2 =10.5⋅3+0.5⋅3−2=1，y1⋅1=1y^1 \cdot 1 =1y1⋅1=1（紧约束，支持向量）
x2x^2x2：0.5⋅4+0.5⋅3−2=1.50.5\cdot4 + 0.5\cdot3 -2 =1.50.5⋅4+0.5⋅3−2=1.5，y2⋅1.5=1.5>1y^2 \cdot 1.5 =1.5 >1y2⋅1.5=1.5>1
x3x^3x3：0.5⋅1+0.5⋅1−2=−10.5\cdot1 + 0.5\cdot1 -2 =-10.5⋅1+0.5⋅1−2=−1，y3⋅(−1)=1y^3 \cdot (-1) =1y3⋅(−1)=1（紧约束，支持向量）

所有样本正确分类，最近点函数间隔正好1。

---

7.5 软间隔分类器 (Soft Margin SVM)

当数据不可分，引入松弛ξi\xi_iξi：

min⁡w,b12∥w∥22+C∑ξi \min_{w,b} \frac{1}{2} \|w\|_2^2 + C \sum \xi_i w,bmin21∥w∥22+C∑ξi

s.t. yi(wTxi+b)≥1−ξi,ξi≥0y^i (w^T x^i + b) \ge 1 - \xi_i, \xi_i \ge 0yi(wTxi+b)≥1−ξi,ξi≥0。

推导动机 ：硬间隔太严，允许"违规"但罚款CξiC \xi_iCξi（Hinge损失max⁡(0,1−z)\max(0,1-z)max(0,1−z)）。

对偶同线性，但0≤αi≤C0 \le \alpha_i \le C0≤αi≤C。

变量解释：

• CCC：正则参数，越大越"硬"。
• ξi\xi_iξi：违规距离。

对比表：硬间隔 vs 软间隔

维度	硬间隔 SVM	软间隔 SVM
学习目标	完美分开	允许噪声，平衡误差与间隔
数据效率	需线性可分	鲁棒于噪声/离群点
典型算法	线性SVM原问题	Hinge损失 + C调参
几何解释	所有点外侧	部分点可"入侵"间隔

【直观理解】 ：硬间隔像完美主义者，软间隔像务实派------允许少数"叛徒"越界，但用CCC控制"叛军规模"。物理意义：现实数据有噪声，软间隔提高泛化，像缓冲区允许小震动。

典型例题 ：加噪声点到上例，假设一负类点移近。设C=1C=1C=1，求对偶，得更大ξ\xiξ，间隔稍小但容忍噪声。

验证：测试点分类准确率升（过拟合降）。

---

7.6 非线性SVM与核技巧 (Kernel Trick)

用ϕ(x)\phi(x)ϕ(x)映射到高维：

对偶中替换(xi)Txj→K(xi,xj)=ϕ(xi)Tϕ(xj)(x^i)^T x^j \to K(x^i, x^j) = \phi(x^i)^T \phi(x^j)(xi)Txj→K(xi,xj)=ϕ(xi)Tϕ(xj)。

常见核：多项式K=(xTz+1)pK=(x^T z +1)^pK=(xTz+1)p；高斯K=exp⁡(−∥x−z∥2/2σ2)K=\exp(-\|x-z\|^2 / 2\sigma^2)K=exp(−∥x−z∥2/2σ2)。

推导动机 ：低维不可分，高维可分（"卷积"空间）。核避免显式ϕ\phiϕ，只算内积。

变量解释：

• KKK：核函数，必须半正定（Gram矩阵）。
• σ\sigmaσ：RBF带宽，控制"局部"影响。

【核心思想】：核像"传送门"------不进高维门，就用门计算距离。几何：低维圈圈点，高维拉开成线性。物理：像透镜弯曲空间，让弯路变直。

典型例题 ：XOR问题（非线性），用RBF核σ=1\sigma=1σ=1。

步骤1：计算Gram矩阵。步骤2：对偶求α\alphaα。步骤3：判别f(x)=∑αiyiK(xi,x)+bf(x)=\sum \alpha_i y^i K(x^i,x) +bf(x)=∑αiyiK(xi,x)+b。

验证：带入(0,0)得-1，(0,1)得1，正确分开。

易混：高斯核无限维，泛化好但易过拟合------调σ\sigmaσ。

---

支持向量回归 (SVR)

SVR：回归版SVM，用ϵ\epsilonϵ-不敏感损失。

原问题：

min⁡w,b12∥w∥2+C∑(ξi++ξi−) \min_{w,b} \frac{1}{2} \|w\|^2 + C \sum (\xi_i^+ + \xi_i^-) w,bmin21∥w∥2+C∑(ξi++ξi−)

s.t. ∣yi−(wTxi+b)∣≤ϵ+ξ|y^i - (w^T x^i + b)| \le \epsilon + \xi∣yi−(wTxi+b)∣≤ϵ+ξ 等。

推导动机 ：分类追求间隔，回归追求"管带"------误差≤ϵ\le \epsilon≤ϵ无罚，超则线性罚。

对偶类似，核适用。

【直观理解】 ：像公路两侧护栏，车在ϵ\epsilonϵ内随意，碰栏罚款。支持向量是"碰栏的车"，稀疏解高效。

---

多类SVM与理论基础

多类：一对多，或联合优化min⁡12∥w∥2+C∑ξi\min \frac{1}{2} \|w\|^2 + C \sum \xi_imin21∥w∥2+C∑ξi，约束∀j≠yi:wyiTxi≥wjTxi+1−ξi\forall j \ne y^i: w_{y^i}^T x^i \ge w_j^T x^i +1 - \xi_i∀j=yi:wyiTxi≥wjTxi+1−ξi。

理论：Vapnik定理，VC维h≤min⁡(4r2/ρ2,m)+1h \le \min(4r^2 / \rho^2, m)+1h≤min(4r2/ρ2,m)+1，最大ρ\rhoρ（间隔）最小化复杂度。

【直观理解】：多类像多面墙，每类一墙。理论意义：大间隔=小VC维=好泛化，像宽路少事故。

---

SVM 与 Logistic回归 (LR) 对比

对比表：SVM vs LR

维度	SVM	LR
学习目标	最大间隔（结构风险）	最大似然（经验风险）
数据效率	小样本高维强	大样本需平衡
典型算法	Hinge损失 + 对偶	交叉熵 + 梯度下降
其他	无概率，自带正则；仅支持向量计算	有概率，受分布影响；全样本计算

【核心思想】：SVM"少数决定多数"（支持向量），LR"民主投票"（所有点）。SVM更"精英主义"，适合稀疏高维。

---

序列最小优化 (SMO) 算法

SMO：高效解SVM对偶，迭代更新一对α\alphaα。

流程：选违KKT的α1\alpha_1α1，选使变化大的α2\alpha_2α2，更新α2=α2old+y2(E1−E2)/η\alpha_2 = \alpha_2^{old} + y^2 (E_1 - E_2)/\etaα2=α2old+y2(E1−E2)/η，clip到L,H。

推导动机 ：全QP慢，SMO分解子问题，保持∑αy=0\sum \alpha y=0∑αy=0。

变量解释：

• Ei=f(xi)−yiE_i = f(x^i) - y^iEi=f(xi)−yi：预测误差。
• η=2K12−K11−K22\eta = 2K_{12} - K_{11} - K_{22}η=2K12−K11−K22：二次系数。

【直观理解】：像爬山但两人手拉手（约束），每次只动两人，选"最陡坡"。几何：调整支持向量"拉紧"平面。

典型例题 ：上数据，初始化α=0\alpha=0α=0。步骤1：选α1\alpha_1α1（违KKT）。步骤2：计算η,E\eta, Eη,E更新。迭代至收敛，得同上α∗\alpha^*α∗。

验证：目标函数上升，KKT满足。

难点：变量选择启发式------优先边界点。

第八章 聚类

8.1 聚类简介与距离度量函数

聚类本质上是"物以类聚"------没有标签，就靠数据自身的结构分组。

详细定义

• 有监督学习 ：给定数据集 {xi,yi}i=1N\{x^i, y^i\}_{i=1}^N{xi,yi}i=1N，学习输入 xxx 到输出 yyy 的映射 y=f(x)y = f(x)y=f(x)。
  • 类型：分类（yyy 是类别标签）、回归（yyy 是连续值）、排序（yyy 是有序数值）。
• 无监督学习 ：只给定 {xi}i=1N\{x^i\}_{i=1}^N{xi}i=1N，寻找数据内在结构 z=f(x)z = f(x)z=f(x)。
  • 类型：概率密度估计、聚类（zzz 是簇标号）、降维/可视化。

【直观理解】：有监督像"老师给答案练题"，无监督像"自己摸索规律"。几何上，有监督在标签空间画分界线，无监督在特征空间找"天然团块"。

对比表：有监督 vs. 无监督学习

维度	有监督学习	无监督学习
学习目标	预测标签 yyy，最小化预测误差	发现内在结构 zzz，如分组或压缩
数据效率	需要大量带标签数据，标注昂贵	只需原始数据，易获取但需处理噪声
典型算法	SVM、神经网络（分类/回归）	K均值、GMM、PCA
评价难度	易（准确率/MSE）	难（内部指标如轮廓系数）
应用场景	图像识别、预测	数据探索、异常检测、预处理

为什么无监督学习？

• 原始数据易得，标注贵（"我们缺的不是数据，而是带标签的数据"）。
• 降低存储/计算、降噪、探索性分析、可视化、作为有监督预处理。

【直观理解】：像探矿------有监督是按图挖金，无监督是先勘探地形找矿脉。

典型例题：区分学习类型

数据集：学生成绩 xxx（数学、语文分），yyy：是否及格。

• 步骤1 ：用 xxx 预测 yyy → 有监督。
• 步骤2 ：只用 xxx 分组（如理科生 vs. 文科生） → 无监督（聚类）。
• 验证：无标签时靠"距离"分组，符合现实（相似成绩的学生常一类）。

---

核心概念：聚类的定义与类型

聚类：根据样本间距离/相似度，分成簇（cluster）。原则：簇内相似（距离小），簇间不相似（距离大）。

簇的概念模糊性

同一个数据集可分不同簇数（课件示意图：多少个簇？2/4/6都可能）。

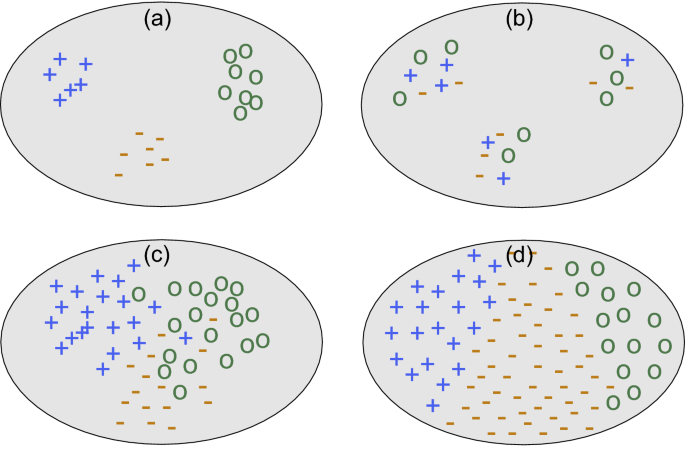
簇的类型

• 基于中心的簇 ：点靠近质心 μk\mu^kμk（球形）。
• 基于邻接的簇：点间连接（链状）。
• 基于密度的簇：高密度区 vs. 低密度分离（任意形状）。
• 基于概念的簇：共享抽象性质（难检测，非以上三种）。

【直观理解】：中心型像"太阳系"（行星围中心）；邻接型像"葡萄串"；密度型像"城市 vs. 郊区"（闹市区连片）；概念型像"交友圈交集"。几何：密度型最灵活，能处理月牙形（K均值办不到）。

聚类的应用

• 客户分群、社交社区、图像分割、异常检测、人类种系分析等。

8.2 三要素

• 自适应性强（样本数、维度、需求）。
• 三要素 ：
  1. 定义"远近"（距离/相似性函数）。
  2. 评价质量（评价函数）。
  3. 获得簇（表示、优化算法、停止条件）。

聚类无绝对正确答案，全看应用。常见坑：数据形状不对选错类型（如球形数据用密度型浪费）。

---

核心概念：距离度量函数（三要素之一）

如何定义样本"远近"？取决于特征类型（数值、类别、文本等）。

详细公式

• 闵可夫斯基距离 （Minkowski）：
  dist(xi,xj)=(∑d=1D∣xi,d−xj,d∣p)1/p \text{dist}(x^i, x^j) = \left( \sum_{d=1}^{D} |x_{i,d} - x_{j,d}|^p \right)^{1/p} dist(xi,xj)=(d=1∑D∣xi,d−xj,d∣p)1/p

  变量解释：

  • xi,xjx^i, x^jxi,xj：D维样本向量。
  • ppp：阶数（控制敏感度）。
  • 特例：
    • p=2p=2p=2：欧氏距离 ∑(xi,d−xj,d)2\sqrt{\sum (x_{i,d} - x_{j,d})^2}∑(xi,d−xj,d)2 。
    • p=1p=1p=1：曼哈顿距离 ∑∣xi,d−xj,d∣\sum |x_{i,d} - x_{j,d}|∑∣xi,d−xj,d∣。
    • p=∞p=\inftyp=∞：切比雪夫距离 max⁡∣xi,d−xj,d∣\max |x_{i,d} - x_{j,d}|max∣xi,d−xj,d∣。

  推导动机 ：从向量范数泛化而来。ppp 大时敏感最大差（极端值主导），ppp 小时平均差。注意：尺度不一致需标准化（否则高量纲特征霸屏）。

• 余弦相似度 （方向敏感，常见于文本）：
  s(xi,xj)=(xi)Txj∥xi∥∥xj∥=∑xi,dxj,d∑xi,d2∑xj,d2 s(x^i, x^j) = \frac{(x^i)^T x^j}{\|x^i\| \|x^j\|} = \frac{\sum x_{i,d} x_{j,d}}{\sqrt{\sum x_{i,d}^2} \sqrt{\sum x_{j,d}^2}} s(xi,xj)=∥xi∥∥xj∥(xi)Txj=∑xi,d2 ∑xj,d2 ∑xi,dxj,d

  变量解释：分子点积（方向重合），分母长度归一。

  推导动机：欧氏测绝对距离，余弦测角度（忽略向量长度）。为什么？文档中"长短文"方向一致就相似。

【直观理解】：欧氏像"直线飞行距离"；曼哈顿像"走马路网格"；余弦像"看两个箭头夹角"（单位圆上投影）。几何：余弦把点投到单位球，完美忽略尺度。物理意义：高维"维度诅咒"时欧氏失效，余弦更稳。

典型例题：计算距离

样本：x1=1,2x^1 = 1, 2x1=1,2，x2=3,4x^2 = 3, 4x2=3,4。

• 步骤1 ：欧氏：(3−1)2+(4−2)2=8≈2.83\sqrt{(3-1)^2 + (4-2)^2} = \sqrt{8} \approx 2.83(3−1)2+(4−2)2 =8 ≈2.83（绝对位置）。
• 步骤2 ：曼哈顿：∣3−1∣+∣4−2∣=4|3-1| + |4-2| = 4∣3−1∣+∣4−2∣=4（网格路径）。
• 步骤3 ：余弦：分子 1⋅3+2⋅4=111\cdot3 + 2\cdot4 = 111⋅3+2⋅4=11，分母 5⋅25≈11.18\sqrt{5} \cdot \sqrt{25} \approx 11.185 ⋅25 ≈11.18，s≈0.98s \approx 0.98s≈0.98（方向几乎相同）。
• 验证 ：若 x2=6,8x^2 = 6,8x2=6,8（倍数），欧氏变大（≈5.66\approx5.66≈5.66），余弦仍 0.980.980.98。符合：余弦只看方向。

聚类性能评价概述

聚类质量的核心追求：簇内相似度越高越好，簇间相似度越低越好 。

评价方法分为两大类：

• 外部评价（external criterion）：把聚类结果和某个"参考标准"（通常是人工标注的真实类别）进行对比
• 内部评价（internal criterion）：只看聚类结果本身，不需要任何参考标签

外部评价 vs 内部评价 对比表

对比维度	外部评价	内部评价
是否需要参考标签	需要（真实类别或专家标注）	不需要
客观性	较高（有标准答案）	较低（主观性强）
适用场景	算法开发、基准测试、学术对比	真实无标签场景、选K值、日常应用
典型指标	JC、FMI、Rand Index	轮廓系数、DBI、Dunn、CHI
计算难度	中等（需计数样本对）	简单到中等（主要算距离）

外部评价指标（需要参考模型）

假设我们有聚类结果 C = {C₁, C₂, ..., Cₖ} 和参考真实类别 C* = {C₁*, ..., Cₖ*}

我们关注的是样本对在两种划分下是否一致，共四种情况：

• a：两种划分都认为同一类（同簇且同真实类）
• b：聚类认为同一类，但真实不同类
• c：聚类认为不同类，但真实同一类
• d：两种划分都认为不同类

三种常用外部指标（都追求越高越好，范围0,1）

1. Jaccard系数 (JC)
   JC=aa+b+c JC = \frac{a}{a + b + c} JC=a+b+ca

   只看"聚类说同类"的对中，有多少真的同类（类似precision，但忽略了d）

2. Fowlkes-Mallows指数 (FMI)
   FMI=aa+b×aa+c FMI = \sqrt{ \frac{a}{a+b} \times \frac{a}{a+c} } FMI=a+ba×a+ca

   几何平均了 precision 和 recall，很平衡

3. Rand指数 (RI)
   RI=2(a+d)N(N−1) RI = \frac{2(a + d)}{N(N-1)} RI=N(N−1)2(a+d)

   整体正确率（把a和d都算作正确）

直观理解

想象你在判断两个人是不是"真朋友"：

• a = 你们俩都觉得是朋友，而且确实是
• b = 你觉得是朋友，其实不是（假阳性）
• c = 你觉得不是朋友，其实是（假阴性）
• d = 你们都觉得不是朋友，也确实不是

JC只看你"说朋友"的时候准不准，RI看整体对错率。

内部评价指标（最常用，无需标签）

核心思想：好的聚类应该

• 簇内点尽可能靠近（紧凑）
• 不同簇尽可能远离（分离）

最重要、最常考的指标：轮廓系数 (Silhouette Index)

对每一个样本点 i 计算：

• a(i)a(i)a(i) = 该点到同簇其他所有点的平均距离（越小越好，表示簇内紧）
• b(i)b(i)b(i) = 该点到最近的另一个簇中所有点的平均距离（越大越好，表示簇间远）

轮廓宽度：
s(i)=b(i)−a(i)max⁡{a(i),b(i)} s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}} s(i)=max{a(i),b(i)}b(i)−a(i)

• s(i)∈−1,1s(i) \in -1, 1s(i)∈−1,1
  • 接近1：非常好（i被很好地聚在自己的簇里）
  • 接近0：i在边界上
  • 负值：i可能被错分到别的簇了

整体轮廓系数：
SI=1N∑i=1Ns(i) SI = \frac{1}{N} \sum_{i=1}^N s(i) SI=N1i=1∑Ns(i)

直观比喻

轮廓系数就像给每个同学打"归属感"分数：

• 坐在自己班中间、离隔壁班很远 → 分很高
• 坐在门口、跟隔壁班更亲近 → 分很低甚至负分

其他常用内部指标（了解即可，考试常考轮廓）

• DB指数 (Davies-Bouldin Index) ：越小越好
  DBI=1K∑k=1Kmax⁡l≠k(簇内平均距离k+簇内平均距离l两个簇中心距离) DBI = \frac{1}{K} \sum_{k=1}^K \max_{l \neq k} \left( \frac{\text{簇内平均距离}_k + \text{簇内平均距离}_l}{\text{两个簇中心距离}} \right) DBI=K1k=1∑Kl=kmax(两个簇中心距离簇内平均距离k+簇内平均距离l)

• Dunn指数 ：越大越好
  DI=min⁡(簇间最小距离)max⁡(簇内最大直径) DI = \frac{\min(\text{簇间最小距离})}{\max(\text{簇内最大直径})} DI=max(簇内最大直径)min(簇间最小距离)

• Calinski-Harabasz指数 (CHI，也叫方差比准则) ：越大越好，计算快，常用于自动选K
  CHI=tr(B)tr(W)×N−KK−1 CHI = \frac{\text{tr}(B)}{\text{tr}(W)} \times \frac{N-K}{K-1} CHI=tr(W)tr(B)×K−1N−K

  （tr(B)反映簇间散布，tr(W)反映簇内散布，像方差分析的F值）

典型例题（手动计算轮廓系数）

假设有3个点，欧氏距离：

• 点A、B在簇1，dist(A,B)=2
• 点C在簇2
• dist(A,C)=5，dist(B,C)=5

计算点A的轮廓系数：

1. a(A) = 到同簇点B的距离 = 2
2. b(A) = 到最近其他簇（簇2）的平均距离 = 5
3. s(A) = (5 - 2) / max(5, 2) = 3/5 = 0.6

同理 s(B)=0.6，s( C)（单点簇，a( C)=0，b( C)=5）= (5-0)/5 = 1.0

平均轮廓系数 ≈ (0.6 + 0.6 + 1.0)/3 ≈ 0.73 → 聚类质量较好

如果把C挪到簇1里，所有点间距变小，a(i)大幅增加，s(i)会下降甚至变负 → 说明合并后质量变差。

总结

外部评价看"和标准像不像"，内部评价看"自己整不整齐"。

实际项目里主要靠轮廓系数 + CHI 来判断聚类好坏和选K值。

聚类算法总体框架

聚类算法主要分四类（按聚类类型分类）：

• 基于中心的：如K均值（K-means）、K-medoids（用中位数代替均值）
• 基于概率分布的：如高斯混合模型（GMM）+ EM算法
• 基于连接性的：如层次聚类（Hierarchical Clustering）
• 基于密度的：如DBSCAN、Mean Shift

算法分类对比表（方便你快速区分）

算法类型	代表算法	簇形状假设	需要预设K？	对噪声/离群点鲁棒性	典型缺点
基于中心	K-means, K-medoids	球形/凸形	是	差（易受离群影响）	非凸、初始化敏感、假设簇等大
基于概率	GMM + EM	椭球形	是	中等	计算慢、收敛慢
基于连接	层次聚类	任意	否	中等	不可逆、链式效应
基于密度	DBSCAN	任意	否	强	参数ε、MinPts敏感

K均值聚类（K-means）------核心算法

问题定义

给定N个样本 {xi}i=1N\{x^i\}_{i=1}^N{xi}i=1N，分成K个簇。输入：数据D、簇数K。

基本算法流程（PAGE 31）：

1. 随机选K个点作为初始中心 μ1,...,μK\mu^1, \dots, \mu^Kμ1,...,μK
2. 重复直到收敛：
   • 每个样本 xix^ixi 分配到最近的中心：zi=arg⁡min⁡k∥xi−μk∥2z_i = \arg\min_k \|x^i - \mu^k\|^2zi=argmink∥xi−μk∥2
   • 更新每个中心：μk=1∣Ck∣∑xi∈Ckxi\mu^k = \frac{1}{|C_k|} \sum_{x^i \in C_k} x^iμk=∣Ck∣1∑xi∈Ckxi

优化目标（损失函数）

平方误差和（SSE）：
J=∑i=1N∑k=1Kri,k∥xi−μk∥2 J = \sum_{i=1}^N \sum_{k=1}^K r_{i,k} \|x^i - \mu^k\|^2 J=i=1∑Nk=1∑Kri,k∥xi−μk∥2

其中 ri,k=1r_{i,k} = 1ri,k=1 如果 xix^ixi 属于簇k，否则0（硬分配）。

变量解释

• ri,kr_{i,k}ri,k：从属指示（硬0/1）
• μk\mu^kμk：第k簇的质心
• JJJ：总平方误差，越小越好

推导动机

J本质是"点到自己簇中心的距离平方和"。为什么平方？放大远点惩罚，优化时更稳定（类似梯度下降）。

迭代优化（鸡生蛋问题）

• 固定 μk\mu^kμk → 分配 ri,kr_{i,k}ri,k（最近邻）
• 固定 ri,kr_{i,k}ri,k → 更新 μk\mu^kμk（均值）
  交替下降J，J单调递减 → 一定收敛。

收敛性

• 坐标下降法，J非凸 → 收敛到局部最优（可能震荡，但实际少见）
• 解：多次运行，取J最小的结果

初始化方法

随机初始化容易坏------K-means++（scikit-learn默认）：

1. 随机选第一个中心
2. 后续中心按距离平方概率选（远点概率大）
   → 质心初始远离，收敛更快更好

K的选择

• 肘部法：画K vs J曲线，找"拐点"
• 轮廓系数/CHI：K增加时，质量先升后降，取峰值
• Gap Statistic、交叉验证（监督任务上用）

K-means的局限性

• 假设簇球形、等大小、等密度 → 非球形/不同密度会崩
• 离群点拉偏中心
• 硬分配 → 小扰动可能跳簇
• 改进：用GMM（软分配+椭球）、DBSCAN（密度）、K-medoids（中位数抗噪）

直观理解

K-means像"抢地盘"：每个中心是国王，点谁近谁的兵。迭代就是"国王换位置，士兵再站队"。几何：每次更新中心是"质心"（重心），像物理平衡。坑点：如果初始国王选得差，就只能抢到小地盘（局部最优）。

典型例题：手动迭代一次K-means

数据：2D点

A(1,1), B(2,1), C(1,2), D(6,6), E(7,7), F(6,7)

设K=2，初始中心 μ1=(2,1.5)\mu_1 = (2,1.5)μ1=(2,1.5)（红），μ2=(6.5,6.5)\mu_2 = (6.5,6.5)μ2=(6.5,6.5)（蓝）

步骤1：计算每个点到两个中心的距离（欧氏）

• A到μ1\mu_1μ1：(1−2)2+(1−1.5)2=1+0.25=1.12\sqrt{(1-2)^2 + (1-1.5)^2} = \sqrt{1+0.25}=1.12(1−2)2+(1−1.5)2 =1+0.25 =1.12
  到μ2\mu_2μ2：(1−6.5)2+(1−6.5)2≈7.78\sqrt{(1-6.5)^2 + (1-6.5)^2} \approx 7.78(1−6.5)2+(1−6.5)2 ≈7.78 → 分到簇1
• 同理：B、C到簇1；D、E、F到簇2

步骤2 ：更新中心

簇1：A,B,C → μ1new=((1+2+1)/3,(1+1+2)/3)=(1.33,1.33)\mu_1^{new} = ( (1+2+1)/3, (1+1+2)/3 ) = (1.33, 1.33)μ1new=((1+2+1)/3,(1+1+2)/3)=(1.33,1.33)

簇2：D,E,F → μ2new=(6.33,6.67)\mu_2^{new} = (6.33, 6.67)μ2new=(6.33,6.67)

步骤3：验证新分配（重新算距离）

• 所有点分配不变 → 收敛
• J下降（新中心更近）

如果初始中心选差 （如μ1=(1,1),μ2=(7,7)\mu_1=(1,1), \mu_2=(7,7)μ1=(1,1),μ2=(7,7)）

• 迭代后可能把A,B,C,D,E,F全分到一簇 → 坏结果
  → 证明初始化关键！

总结

K-means是"简单暴力"的聚类王者：快、易并行、适合大数据。但记住它的假设（球形簇），数据不对就换GMM或DBSCAN。

8.3 高斯混合模型（GMM）+ EM算法

高斯混合模型（Gaussian Mixture Model, GMM） ，它可以看作是K-means的概率版、软分配版、椭球版。

为什么需要GMM？（K-means的痛点）

K-means的假设太强了：

• 每个点100%属于一个簇（硬分配）→ 边界点容易跳来跳去
• 簇必须是球形且方差差不多（欧氏距离+均值）
• 所有簇出现概率相等（π_k = 1/K）

现实数据经常是椭球形、不同大小、不同密度 → K-means直接裂开。

GMM的直观想法

我们假设数据是由K个高斯分布"混合"生成的：

• 先按概率π_k抽一个高斯成分k（k=1,...,K）
• 再从这个高斯N(μ_k, Σ_k)里采样一个点

这样：

• 簇可以是任意方向、大小的椭球（靠协方差Σ_k）
• 每个点属于每个簇都有概率（软分配）
• 不同簇可以有不同权重π_k

GMM模型公式

观测数据概率密度：
p(x)=∑k=1KπkN(x∣μk,Σk) p(x) = \sum_{k=1}^K \pi_k \mathcal{N}(x | \mu_k, \Sigma_k) p(x)=k=1∑KπkN(x∣μk,Σk)

其中：

• πk\pi_kπk：混合系数，∑πk=1\sum \pi_k = 1∑πk=1
• N(x∣μk,Σk)\mathcal{N}(x | \mu_k, \Sigma_k)N(x∣μk,Σk)：均值μ_k、协方差Σ_k的高斯

目标：用最大似然估计参数θ = {π_k, μ_k, Σ_k}

对数似然：
ℓ(θ)=∑i=1Nlog⁡(∑k=1KπkN(xi∣μk,Σk)) \ell(\theta) = \sum_{i=1}^N \log \left( \sum_{k=1}^K \pi_k \mathcal{N}(x^i | \mu_k, \Sigma_k) \right) ℓ(θ)=i=1∑Nlog(k=1∑KπkN(xi∣μk,Σk))

问题：log里还有sum → 直接求导=0没有闭式解，参数耦合严重 → 无法直接优化。

解决方案：引入隐变量z（EM算法登场）

为每个样本xⁱ引入一个K维独热隐变量zⁱ（z^i_k = 1表示来自第k个高斯）

联合分布：
p(x,z)=∏k=1KπkN(x∣μk,Σk)zk p(x, z) = \prod_{k=1}^K \\pi_k \\mathcal{N}(x \| \\mu_k, \\Sigma_k)^{z_k} p(x,z)=k=1∏KπkN(x∣μk,Σk)zk

完整数据对数似然（如果z已知就简单了）：
ℓc(θ)=∑i=1N∑k=1Kziklog⁡πk+log⁡N(xi∣μk,Σk) \ell_c(\theta) = \sum_{i=1}^N \sum_{k=1}^K z_{i k} \left \\log \\pi_k + \\log \\mathcal{N}(x\^i \| \\mu_k, \\Sigma_k) \\right ℓc(θ)=i=1∑Nk=1∑Kziklogπk+logN(xi∣μk,Σk)

z未知 → 用EM算法迭代"猜z → 更新参数 → 再猜z"。

EM算法两步（超级好记）

E步（Expectation） ：用当前参数算每个点属于每个簇的后验概率（软分配）
rik≜P(zik=1∣xi,θold)=πkoldN(xi∣μkold,Σkold)∑jπjoldN(xi∣μjold,Σjold) r_{i k} \triangleq P(z_{i k}=1 | x^i, \theta^{\text{old}}) = \frac{\pi_k^{\text{old}} \mathcal{N}(x^i | \mu_k^{\text{old}}, \Sigma_k^{\text{old}})}{\sum_{j} \pi_j^{\text{old}} \mathcal{N}(x^i | \mu_j^{\text{old}}, \Sigma_j^{\text{old}})} rik≜P(zik=1∣xi,θold)=∑jπjoldN(xi∣μjold,Σjold)πkoldN(xi∣μkold,Σkold)

r_{i k} ∈ 0,1，∑k r{i k} = 1 → 就是"责任"（responsibility）

M步（Maximization） ：用r当权重，更新参数（加权版本的均值、协方差、混合系数）
πknew=∑irikN \pi_k^{\text{new}} = \frac{\sum_i r_{i k}}{N} πknew=N∑irik
μknew=∑irikxi∑irik \mu_k^{\text{new}} = \frac{\sum_i r_{i k} x^i}{\sum_i r_{i k}} μknew=∑irik∑irikxi
Σknew=∑irik(xi−μknew)(xi−μknew)T∑irik \Sigma_k^{\text{new}} = \frac{\sum_i r_{i k} (x^i - \mu_k^{\text{new}})(x^i - \mu_k^{\text{new}})^T}{\sum_i r_{i k}} Σknew=∑irik∑irik(xi−μknew)(xi−μknew)T

直观理解

• E步：每个点对每个簇说"我有多大概率是你生的？"（软投票）
• M步：每个簇根据"收到的票数"重新调整自己的位置、大小、影响力
• 反复迭代，直到每个人都找到"最可能生自己的簇"

GMM vs K-means 终极对比表

项目	K-means	GMM + EM
分配方式	硬分配（0或1）	软分配（概率r_{ik} ∈ 0,1）
簇形状	只能球形（隐含Σ_k = σ²I）	任意椭球（完整协方差Σ_k）
簇大小/密度	假设差不多	自然不同（不同Σ_k）
簇权重π_k	强制相等（1/K）	可学习（不同大小的簇）
优化目标	最小化SSE（平方误差和）	最大化对数似然
当Σ_k→0且π_k相等时	等价！（GMM退化成K-means）	-
对噪声/离群点	敏感（拉偏中心）	更鲁棒（概率小）

极限情况下GMM = K-means

当我们强制：

• 所有Σ_k = ε²I（ε→0）
• 所有π_k = 1/K

→ r_{i k}要么≈1要么≈0 → 退化成硬分配 → 完全等价于K-means

所以可以说："GMM是K-means的泛化"

收敛性

EM每次迭代都严格提升（或保持）对数似然ℓ(θ)ℓ(θ)ℓ(θ)，所以一定会收敛（通常到局部最优）。实际跑几百步就稳了。

典型例题（手算一轮EM）

2个1维点：x¹=2, x²=8，K=2

初始：π₁=π₂=0.5, μ₁=1, μ₂=10, Σ₁=Σ₂=1（方差1）

E步（算r）：

• 对x¹=2：
  N(2|1,1) = 高斯密度 ≈ 0.242
  N(2|10,1) ≈ 很小≈0
  r_{11} ≈ 1, r_{12} ≈ 0
• 对x²=8：r_{21} ≈ 0, r_{22} ≈ 1

M步：

• π₁ = (1+0)/2 = 0.5
• μ₁ = (12 + 08)/1 = 2
• μ₂ = (02 + 18)/1 = 8
• Σ更新类似（这里方差固定）

第二次E步已经完全硬分配，收敛。

（如果初始μ₁=3, μ₂=7，第一次r就不会100%，需要多轮慢慢拉开）

总结

GMM+EM就是"概率版K-means"：

• E步 ≈ K-means的分配（但软）
• M步 ≈ K-means的更新中心（但加权，还更新协方差和π）

一句话总结就是：K-means是特殊的GMM，GMM是更强的K-means。

8.4 层次聚类

**层次聚类（Hierarchical Clustering）**是"基于连接性"的聚类，不需要预设K，能生成树状结构（dendrogram），适合探索数据（如生物分类树）。相比K-means/GMM，它更"灵活"，但计算慢点。重点是凝聚式（最常见）和簇间相似性定义（决定算法变体）。

层次聚类的基本想法

• 不是一次性分K个簇，而是生成嵌套的簇树（像家族树）
• 可视化为树状图（dendrogram）：从叶子（单个点）到根（全数据一个簇）
• 切树的不同高度，得不同簇数（不用预设K）

优点

• 不需预设簇数K（后切树选）
• 对应有意义的分类体系（e.g., 生物门纲目科）
• 能处理任意形状（取决于相似性定义）

两种类型

• 凝聚式（Agglomerative，自底向上）：从每个点一个簇开始，递归合并最近的两个簇，直到一个大簇（最流行）
• 分裂式（Divisive，自顶向下）：从全数据一个簇开始，递归分裂最"不一致"的簇（e.g., 直径最大的）

凝聚式算法流程：

1. 计算所有点间相似矩阵
2. 每个点一个簇
3. 重复：合并最近两个簇，更新矩阵
4. 直到一个簇
   

关键：如何定义/更新簇间相似性？ → 不同定义生不同变体

簇间相似性定义

用dist(CkC_kCk, ClC_lCl)测两个簇"远近"。常见方法：

• MIN（Single Link，最小距离） ：dist=min⁡i∈Ck,j∈Cldist(i,j)dist = \min_{i\in C_k, j\in C_l} dist(i,j)dist=mini∈Ck,j∈Cldist(i,j)

  • 优势：任意形状、非凸簇
  • 缺点：链式效应（长链连大簇）
    

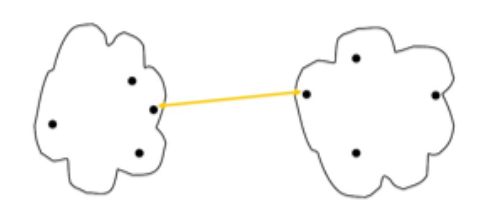
• MAX（Complete Link，最大距离） ：dist=max⁡i∈Ck,j∈Cldist(i,j)dist = \max_{i\in C_k, j\in C_l} dist(i,j)dist=maxi∈Ck,j∈Cldist(i,j)

  • 优势：抗噪鲁棒，不链式
  • 缺点：偏球形，易拆大簇（过度聚类）
    

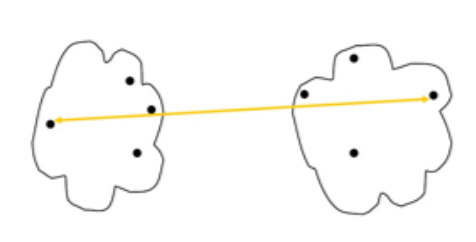
• Group Average（平均距离） ：dist=1∣Ck∣∣Cl∣∑i∈Ck,j∈Cldist(i,j)dist = \frac{1}{|C_k||C_l|} \sum_{i\in C_k, j\in C_l} dist(i,j)dist=∣Ck∣∣Cl∣1∑i∈Ck,j∈Cldist(i,j)

  • 优势：MIN/MAX折中，抗噪+不过度
  • 缺点：计算稍慢

• Centroids（中心距离） ：dist=dist(μk,μl)dist = dist(\mu_k, \mu_l)dist=dist(μk,μl)，μ\muμ 是均值

  • 优势：简单
  • 缺点：反转效应（后合并距可能比前小）

• Ward方法（平方误差） ：dist=ΔSSEdist = \Delta SSEdist=ΔSSE（合并后误差增量）

  • Δ=∣Ck+Cl∣∥μkl−μ∥2−∣Ck∣∥μk−μ∥2−∣Cl∣∥μl−μ∥2\Delta = |C_k + C_l| \|\mu_{kl} - \mu\|^2 - |C_k| \|\mu_k - \mu\|^2 - |C_l| \|\mu_l - \mu\|^2Δ=∣Ck+Cl∣∥μkl−μ∥2−∣Ck∣∥μk−μ∥2−∣Cl∣∥μl−μ∥2
  • 优势：少噪，层次版K-means
  • 缺点：偏球形

不同定义对比表

定义方法	簇形状支持	抗噪性	常见问题	典型场景
MIN	任意/链状	差	链式效应	长链数据（如社交网）
MAX	球形/紧凑	好	过度拆大簇	噪声数据
Average	中等	中等	计算量大	平衡需求
Centroids	球形	中等	反转效应	简单均值数据
Ward	球形	好	倾向小簇	初始化K-means

层次聚类的直观理解

层次聚类像"公司并购"：凝聚式从小公司（点）开始，最近的合并成大集团，树记录过程。相似性定义是"并购标准"------MIN看"最近员工距离"（易链），MAX看"最远员工"（保守）。

几何：树状图如分支树，高切=少簇，低切=多簇。

物理：生物进化树，合并序反映"亲缘远近"。

簇数确定

看树状图：切覆盖最大垂直距的水平线，垂直线数=簇数。

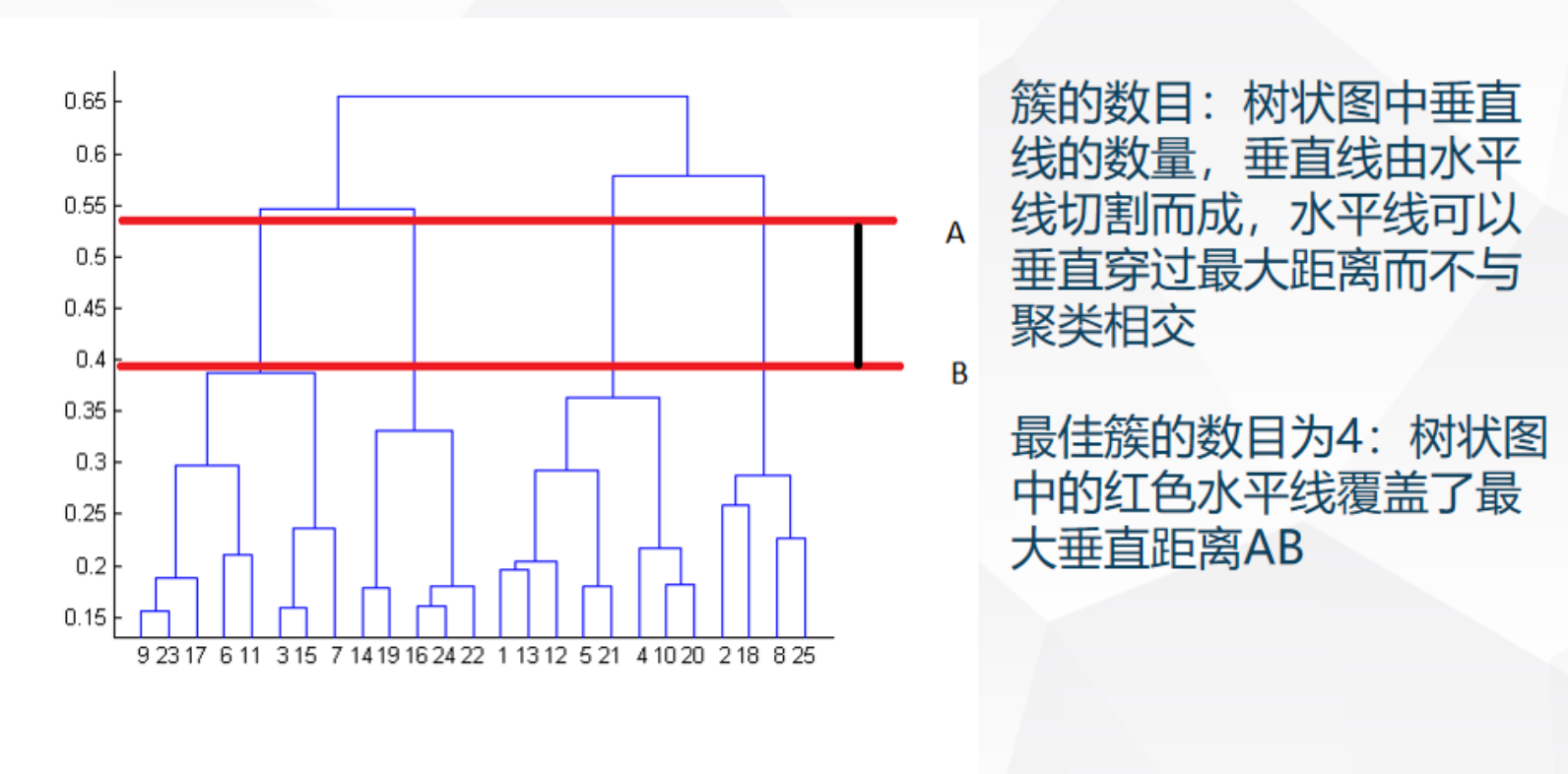
限制

• 贪心，不可逆（合并错没法回）
• 无全局优化（可能局部坏）
• 敏感噪/尺寸/凸形（依方法）
• 计算O(N²)慢，大数据难

典型例题：手动凝聚式聚类（用MIN定义）

5点1D数据：A1=1, A2=2, A3=4, A4=5, A5=10（直观上明显有三簇：1-2,4-5,10）

初始：每个点一簇，相似矩阵（欧氏）：

• 最近：A1-A2=1, A3-A4=1

步骤1：合并A1-A2成C1, A3-A4成C2

• 更新dist(C1,C2)=min(2-4,2-5,1-4,1-5)=2（MIN）
• dist(C1,A5)=min(1-10,2-10)=8
• dist(C2,A5)=min(4-10,5-10)=5

步骤2：最近C2-A5=5，合并成C3=4,5,10

• 更新dist(C1,C3)=min(dist(C1,C2),dist(C1,A5))=2（MIN链式）

步骤3：合并C1-C3=2，全一个簇

树：先并近点，后连远，但MIN链式可能把10连早。

如果用MAX：dist(C1,C2)=max(1-5,2-4)=4，dist(C2,A5)=6 >4，先并C1-C2错（拆大簇问题）。

验证：切树高=3簇（1-2,4-5,10），匹配数据。K-means可能把4-5-10并一簇（均值拉）。

8.5 基于密度的聚类

基于密度的聚类（DBSCAN）

：基于密度的聚类 ，核心代表就是DBSCAN（Density-Based Spatial Clustering of Applications with Noise）。它是"基于密度"的典型，能处理任意形状簇、自动识别噪声、不需要预设K，在实际应用中非常实用（尤其图像分割、异常检测）。

为什么需要基于密度的方法？

K-means和GMM假设簇是"凸的/椭球的"，层次聚类容易链式或过度分裂。

现实数据常有：

• 任意形状（月牙、环形、长条）
• 不同密度
• 噪声/离群点

基于密度直接解决：簇 = 高密度区域连通，低密度是噪声。

DBSCAN核心思想

• 密度 = 指定半径ε内点的个数
• 高密度区连成簇，低密度区隔开簇，孤立点是噪声

三个关键概念：

• 核心点（Core point）：ε邻域内至少有MinPts个点（包括自己）
• 边界点（Border point）：ε邻域内点数 < MinPts，但属于某个核心点的邻域
• 噪声点（Noise/Outlier）：既不是核心也不是边界

密度关系

• 密度直达：q在p的ε邻域，且p是核心 → q由p密度直达
• 密度可达：存在路径，所有中间点都是核心 → 形成簇
• 密度相连：存在共同核心点o，使p和q都密度可达o

簇定义：最大密度相连点集（连通 + 最大性）

DBSCAN算法流程

输入：数据D，ε（半径），MinPts（最小点数）

1. 初始化核心点集合Ω = ∅，未访问点Γ = D
2. 遍历所有点，计算每个点的ε邻域N(x^i)：
   • 如果 |N(x^i)| ≥ MinPts → x^i 是核心点，加入Ω
3. while Ω 不为空：
   • 随机选一个核心点o ∈ Ω，初始化队列Q = {o}
   • 从Γ移除o
   • while Q 不为空：
     • 取出q ∈ Q
     • 如果q是核心点：
       • 找q的邻域中未访问点Δ = N(q) ∩ Γ
       • 把Δ加到Q，Γ移除Δ
   • 生成一个新簇C_k = 本轮访问的所有点
   • K = K + 1
4. 剩余Γ中的点是噪声

参数解释

• ε：邻域半径（太小→太多噪声，太大→全连成一个簇）
• MinPts：通常取维度+1或经验值（如2*dim）

优势 vs 劣势对比表

方面	优势	劣势
簇形状	任意形状（非凸、链状、环形都OK）	-
簇数	自动确定（不用预设K）	-
噪声处理	自动识别离群点	-
参数	只有ε和MinPts（相对简单）	参数敏感（选错ε/MinPts会崩）
密度差异	能处理均匀密度	密度差异太大时效果差（需预处理）
时间复杂度	O(N log N)（用KD树加速）	最坏O(N²)（无索引时）

如何选参数ε和MinPts？

经典方法：k-距离图（k=MinPts）

• 对每个点算到第k最近邻的距离
• 排序画图（x轴=点，y轴=距离）
• 图通常急剧上升前有个"膝盖"（elbow），膝盖处的距离 ≈ 合适ε
• MinPts经验：2*维度，或10~20（小数据集）

典型例题：手动理解DBSCAN

假设2D点（简化，ε=1.5, MinPts=3）：

• 点群1：密集三角形（5点在小圈内）
• 点群2：稀疏环形（10点绕圈）
• 3个孤立噪声点

过程：

1. 找核心点：群1全核心（邻域≥3），群2部分核心（环上密度够），噪声无
2. 从群1核心扩展：密度直达/可达，生成簇1
3. 跳到群2核心：扩展成环形簇2（密度连通绕圈）
4. 剩余孤立点 → 噪声

结果：簇1（圆）、簇2（环）、噪声（3点）------K-means/GMM全失败。

注意

DBSCAN是"无假设王者"：不假设形状、不假设数量、不怕噪声，但参数选错就全废。

实际用时，先画k-距离图选ε，再调MinPts。sklearn里DBSCAN直接用。

8.5 聚类小结

聚类是无监督学习的核心任务 ，高度依赖应用场景，几乎没有"万能算法"。

核心一句话：没有最好的聚类方法，只有最适合数据的聚类方法。

聚类方法的四大类型对比（回顾+总结）

类型	代表算法	是否需预设K	簇形状支持	对噪声/离群点	典型应用场景	最大优点	最大缺点
基于中心	K-means, K-medoids	是	球形/凸	差	大规模均匀数据、初探	简单、快、可扩展	假设太强、易受初始/噪声影响
基于概率	GMM + EM	是	椭球/任意	中等	需要软分配、不同密度/大小	概率解释、软分配	计算慢、局部最优
基于连接	层次聚类（凝聚/分裂）	否	任意	中等	探索性分析、需要树状结构	不需K、层次可视化	不可逆、计算O(N²)
基于密度	DBSCAN, OPTICS	否	任意	强	噪声多、任意形状、异常检测	自动噪声、任意形状	参数敏感、密度差异大时失效

一句话总结

• 不知道K、想探索 → 层次聚类或DBSCAN
• 大数据、简单球形 → K-means
• 需要概率/软分配/椭球 → GMM
• 噪声多、形状怪 → DBSCAN首选

sklearn中的聚类工具

sklearn.cluter模块几乎囊括了所有主流算法，直接import就能用。常用类列表：

• KMeans / MiniBatchKMeans：大规模数据首选
• DBSCAN：密度聚类王者
• AgglomerativeClustering：层次聚类（支持Ward、complete、average等链接）
• GaussianMixture：GMM + EM（软分配）
• MeanShift：基于密度，但自动带宽
• SpectralClustering：谱聚类（高维非凸好用）
• Birch：平衡迭代缩减层次聚类（大数据友好）

使用示例

from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering, GaussianMixture

# K-means 示例
kmeans = KMeans(n_clusters=3, init='k-means++', n_init=10)
labels = kmeans.fit_predict(X)

# DBSCAN（自动找噪声）
db = DBSCAN(eps=0.5, min_samples=5)
labels = db.fit_predict(X)  # -1 表示噪声

# GMM 软分配
gmm = GaussianMixture(n_components=3)
gmm.fit(X)
probs = gmm.predict_proba(X)  # 每个点的概率分布

课件的思考题

这里给出简要的答案：

1. K均值聚类算法隐含了对簇的什么假设？

   → 球形簇、等大小、等密度、每个点硬分配（欧氏距离+均值中心）

2. K均值迭代一定会收敛吗？

   → 会 （J单调递减，有下界），但收敛到局部最优，多次运行取最好

3. K均值算法的初始化参数怎么选择？

   → k-means++（按距离平方概率选，远离已有中心）→ scikit默认

4. K均值算法的超参K怎么选择？

   → 肘部法（SSE vs K曲线拐点）、轮廓系数/CHI峰值、Gap Statistic、领域知识

5. K均值算法有什么局限性？可能用什么方法改进？

   → 局限：非球形/不同密度/噪声/硬分配

   → 改进：GMM（软+椭球）、DBSCAN（密度+任意形）、K-medoids（中位数抗噪）

6. 基于GMM的EM聚类算法为什么要引入隐变量z？

   → 因为直接最大化不完整数据似然难求导，引入z后完整数据似然简单，E步猜z概率，M步更新参数

7. K均值和EM算法有什么共通之处？

   → 都是交替优化（分配↔更新中心），E步≈K-means分配，M步≈更新均值（GMM极限退化成K-means）

8. 如何度量簇的相似性？不同度量方法的优缺点？

   → 见上表：MIN（任意形但链式）、MAX（抗噪但偏球）、Average（平衡）、Ward（层次K-means）

9. 层次聚类的限制有哪些？

   → 贪心不可逆、无全局优化、对噪/尺寸/凸敏感、计算慢