文章目录
-
- [第17题:KV Cache 计算](#第17题:KV Cache 计算)
- [第18题:RoPE 旋转位置编码](#第18题:RoPE 旋转位置编码)
- [第19题:Transformer Block 的 Post-norm 和 Pre-norm](#第19题:Transformer Block 的 Post-norm 和 Pre-norm)
- [第20题:Gated Attention 的 Output 计算](#第20题:Gated Attention 的 Output 计算)
- [第21题:GPT-OSS 20B 架构分析](#第21题:GPT-OSS 20B 架构分析)
- [第22题:Roofline Model 分析](#第22题:Roofline Model 分析)
- [第23题:Operation Intensity 计算](#第23题:Operation Intensity 计算)
- [第24题:A100 Operation Intensity 分析](#第24题:A100 Operation Intensity 分析)
第17题:KV Cache 计算
假设我们要在一台服务器上对一个采用多头注意力(MHA)的 Transformer 模型进行推理。模型参数如下:隐藏层维度 d = 4096 d=4096 d=4096,层数 L = 32 L=32 L=32,注意力头数 h = 32 h=32 h=32,采用 FP16 半精度存储(每个元素占 2 Bytes)。
- 请给出生成第 N N N个 token 时,KV Cache 新增存储占用的计算公式。
- 当 Batch Size B = 1 B=1 B=1,序列长度达到 N = 1024 N=1024 N=1024时,请计算该请求在显存中占用的 KV Cache 总量(单位:MB)。
解:
- 生成第 个 token 时,每一层需要存储该 token 的 Key 和 Value 向量。每个元素占 2 Bytes(FP16)
T o t a l K V C a c h e = B × N × L × 2 × d × 2 Bytes = 4 B L d Bytes Total KV Cache=B×N×L×2×d×2\text{Bytes}= 4BLd \text{Bytes} TotalKVCache=B×N×L×2×d×2Bytes=4BLdBytes
第一个2是k、v各一份 - 1 MB = 1024 × 1024 Bytes 1 \text{ MB} = 1024 \times 1024 \text{ Bytes} 1 MB=1024×1024 Bytes
Total = B × N × L × 2 × ( d h × h ) × 2 Bytes = 1 × 1024 × 32 × ( 2 × 4096 × 2 ) Bytes = 512 M B \begin{aligned} \text{Total}&=B×N×L×2×(\frac{d}{h}×h)×2\text{Bytes} \\ &= 1\times 1024 \times 32 \times (2 \times 4096 \times 2) \text{ Bytes} \\ &= 512MB \end{aligned} Total=B×N×L×2×(hd×h)×2Bytes=1×1024×32×(2×4096×2) Bytes=512MB
第18题:RoPE 旋转位置编码
对于位置 m m m的查询向量 q m q_m qm和位置 n n n的键向量 k n k_n kn:
- 证明旋转位置编码(RoPE)下变换后的向量 q ~ m \tilde{q}_m q~m 和 k ~ n \tilde{k}_n k~n的点积仅和 q m q_m qm、 k n k_n kn及相对位置 m − n m-n m−n相关;
- 进一步说明 RoPE 会对 q/k/v 向量中的哪几个进行位置信息注入。
提示:RoPE 通过旋转矩阵 R p o s R_{pos} Rpos将位置信息注入向量。
解:
在 RoPE(Rotary Position Embedding)中,对位于位置 m m m的向量做旋转编码:
q ~ m = R ( m ) q m , k ~ n = R ( n ) k n \tilde q_m = R(m)q_m, \quad \tilde k_n = R(n)k_n q~m=R(m)qm,k~n=R(n)kn
计算 RoPE 后的点积
q ~ m ⊤ k ~ n = ( R ( m ) q m ) ⊤ ( R ( n ) k n ) = q m ⊤ R ( m ) ⊤ R ( n ) k n = q m ⊤ R ( n − m ) k n \tilde q_m^\top \tilde k_n = (R(m) q_m)^\top (R(n) k_n) = q_m^\top R(m)^\top R(n) k_n=q_m^\top R(n-m) k_n q~m⊤k~n=(R(m)qm)⊤(R(n)kn)=qm⊤R(m)⊤R(n)kn=qm⊤R(n−m)kn
q ~ m ⊤ k ~ n 仅依赖于 q m , k n 和相对位置 ( m − n ) \tilde q_m^\top \tilde k_n\text{ 仅依赖于 } q_m, k_n \text{ 和相对位置 } (m-n) q~m⊤k~n 仅依赖于 qm,kn 和相对位置 (m−n),不依赖绝对位置 (m) 或 (n),只编码了相对位置信息。如果在更高维度的情况下,RoPE 将向量分成多个二维子空间,每个子空间独立应用旋转,结论同样成立。
RoPE 只作用于 Q u e r y 和 K e y ,不对 V a l u e 向量进行编码 \text{RoPE 只作用于 } Query \text{ 和 } Key,不对Value向量进行编码 RoPE 只作用于 Query 和 Key,不对Value向量进行编码
即: q → q ~ = R ( p o s ) , q q \rightarrow \tilde q = R(pos), q q→q~=R(pos),q, k → k ~ = R ( p o s ) , k k \rightarrow \tilde k = R(pos), k k→k~=R(pos),k
而: v 不进行 RoPE 旋转 v \text{ 不进行 RoPE 旋转} v 不进行 RoPE 旋转
why:
- Attention 权重由 softmax ( q ⊤ k d ) \text{softmax}\left(\frac{q^\top k}{\sqrt{d}}\right) softmax(d q⊤k)决定,位置关系只需影响 q·k 相似度
- Attention ( i ) = ∑ j = 1 L α i j v j \text{Attention}(i) = \sum_{j=1}^{L} \alpha_{ij} v_j Attention(i)=∑j=1Lαijvj加权求和输出,此时 v v v只负责进行内容聚合,不需要显式位置编码
第19题:Transformer Block 的 Post-norm 和 Pre-norm
对于 Transformer Block 的 Post-norm 有:
x l + 1 = x l + Sublayer ( x l ) y l + 1 = LN ( x l + 1 ) x_{l+1}=x_l + \text{Sublayer}(x_l)\\ y_{l+1}=\text{LN}(x_{l+1}) xl+1=xl+Sublayer(xl)yl+1=LN(xl+1)
- 请相应给出 Pre-norm 的计算公式;
- 结合梯度分析证明 Post-norm 相比 Pre-norm 更易出现梯度消失或放大,并指出其中的梯度恒等映射通路。
解:
Pre-Norm将LayerNorm应用在Sublayer之前
y l = LN ( x l ) x l + 1 = x l + Sublayer ( y l ) y_l = \text{LN}(x_l)\\x_{l+1} = x_l + \text{Sublayer}(y_l) yl=LN(xl)xl+1=xl+Sublayer(yl)
Pre-norm 由于存在梯度恒等映射通路(residual connection 在 LayerNorm 之后),梯度更稳定;Post-norm 的梯度需要先经过 LayerNorm,更容易出现梯度消失或放大。
Pre-norm 的梯度通路
x l + 1 = x l + Sublayer ( LN ( x l ) ) x_{l+1} = x_l + \text{Sublayer}(\text{LN}(x_l)) xl+1=xl+Sublayer(LN(xl))
反向传播:
∂ L ∂ x l = ∂ L ∂ x l + 1 ( I + ∂ Sublayer ∂ x ^ l ∂ LN ∂ x l ) \frac{\partial \mathcal{L}}{\partial x_l}=\frac{\partial \mathcal{L}}{\partial x_{l+1}}\Big(I+\frac{\partial \text{Sublayer}}{\partial \hat x_l}\frac{\partial \text{LN}}{\partial x_l}\Big) ∂xl∂L=∂xl+1∂L(I+∂x^l∂Sublayer∂xl∂LN)
- 存在一条恒等映射梯度通路 I I I
- 无论子层或 LN 如何变化,梯度都能直接传回
Post-norm 的梯度通路
y l + 1 = LN ( x l + Sublayer ( x l ) ) y_{l+1} = \text{LN}(x_l + \text{Sublayer}(x_l)) yl+1=LN(xl+Sublayer(xl))
反向传播:
∂ L ∂ x l = ∂ L ∂ y l + 1 ⋅ ∂ LN ∂ x l + 1 ⋅ ( I + ∂ Sublayer ∂ x l ) \frac{\partial \mathcal{L}}{\partial x_l}=\frac{\partial \mathcal{L}}{\partial y_{l+1}}\cdot\frac{\partial \text{LN}}{\partial x_{l+1}}\cdot\Big(I+\frac{\partial \text{Sublayer}}{\partial x_l}\Big) ∂xl∂L=∂yl+1∂L⋅∂xl+1∂LN⋅(I+∂xl∂Sublayer)
- 梯度必须经过 LN 的 Jacobian Jacobian(雅可比矩阵)是一个多元函数的一阶导数矩阵
- 不存在"纯恒等"的梯度直通路径
LayerNorm梯度放缩效应:
LN ( x ) = x − μ σ , 于是 ∣ ∂ LN ∂ x ∣ ≈ O ( 1 σ ) \text{LN}(x) = \frac{x - \mu}{\sigma} ,于是\left| \frac{\partial \text{LN}}{\partial x} \right| \approx \mathcal{O}\left(\frac{1}{\sigma}\right) LN(x)=σx−μ,于是 ∂x∂LN ≈O(σ1)
当堆叠 L L L层 Post-norm block: ∏ l = 1 L ∂ LN ∂ x l \prod_{l=1}^{L} \frac{\partial \text{LN}}{\partial x_l} ∏l=1L∂xl∂LN
- 若 σ > 1 \sigma > 1 σ>1 → 梯度 指数衰减
- 若 σ < 1 \sigma < 1 σ<1 → 梯度 指数放大
梯度消失 / 爆炸更容易出现
Pre-norm 梯度中始终含有: ∏ l = 1 L I = I \prod_{l=1}^{L} I = I ∏l=1LI=I
- 梯度不会被 LN 连乘放缩
- 深层 Transformer 更稳定
第20题:Gated Attention 的 Output 计算
已知 MHA 中第 k 层第 i 位置 token 的 output 表征计算如下:

请相应给出下图 Gated Attention 中 G1/G2/G3 对应的 output o i k o_i^k oik计算方法。
注意:可用 Non-Linearity-Map \text{Non-Linearity-Map} Non-Linearity-Map算子表示 element-wise gatting 机制,即 Y ′ = Y ⊙ σ ( X W θ ) = Non-Linearity-Map(Y) Y' = Y \odot \sigma(X W_\theta) = \text{Non-Linearity-Map(Y)} Y′=Y⊙σ(XWθ)=Non-Linearity-Map(Y)。
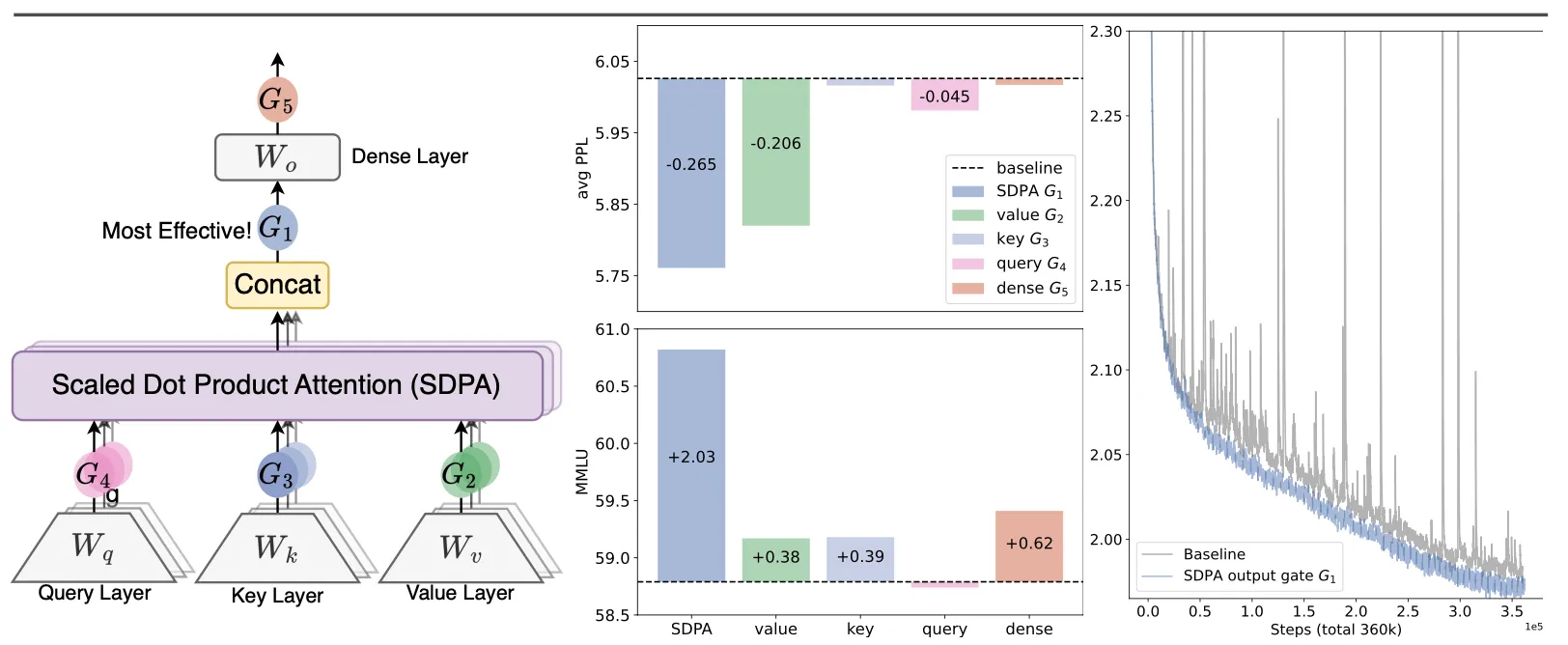
解:
G1:Output / Dense Gating 在 Concat 之后、Dense Layer 之前应用门控
它对 Attention 聚合后的上下文向量进行门控处理。即对公式中括号内的加权求和结果进行 Gating。
H i k = ∑ j = 0 i S i j k ⋅ X j W V k H_i^k=\sum_{j=0}^i S_{ij}^k \cdot X_j W_V^k Hik=∑j=0iSijk⋅XjWVk
对聚合结果应用门控后再进行输出投影 o i , G 1 k = Non-Linearity-Map ( H i k ) ⋅ W O k = Non-Linearity-Map ( ∑ j = 0 i S i j k ⋅ X j W V k ) ⋅ W O k o_{i,G_1}^k = \text{Non-Linearity-Map}\left( H_i^k\right)\cdot W_O^k=\text{Non-Linearity-Map}\left( \sum_{j=0}^i S_{ij}^k \cdot X_j W_V^k \right)\cdot W_O^k oi,G1k=Non-Linearity-Map(Hik)⋅WOk=Non-Linearity-Map(j=0∑iSijk⋅XjWVk)⋅WOk
G2:Value Gating
o i , G2 k = ( ∑ j = 0 i S i j k ⋅ Non-Linearity-Map ( X j W V k ) Z ) W O k o_{i,\text{G2}}^k = \left(\sum_{j=0}^i S_{ij}^k \cdot \text{Non-Linearity-Map}(X_j W_V^k)Z\right)W_O^k oi,G2k=(j=0∑iSijk⋅Non-Linearity-Map(XjWVk)Z)WOk
G3:Key Gating(影响 attention score)
K ~ j k = Non-Linearity-Map ( X j W K k ) \tilde K_j^k = \text{Non-Linearity-Map} (X_jW_K^k) K~jk=Non-Linearity-Map(XjWKk)
Attention score: S i j k = Softmax j ( ( X i W Q k ) T ( K ~ j k ) d k ) S_{ij}^k = \text{Softmax}j \left( \frac{(X_i W_Q^k)^T(\tilde K_j^k)}{\sqrt{d_k}} \right) Sijk=Softmaxj(dk (XiWQk)T(K~jk))
o i , G3 k = ( ∑ j = 0 i S i j k ⋅ X j W V k ) W O k o{i,\text{G3}}^k = (\sum_{j=0}^i S_{ij}^k \cdot X_j W_V^k) W_O^k oi,G3k=(j=0∑iSijk⋅XjWVk)WOk
⚠️ Gate 不直接出现在求和式中,而是通过改变 S i j k S_{ij}^k Sijk 间接影响输出
第21题:GPT-OSS 20B 架构分析
GPT-OSS 20B 架构相比标准 Transformer 有多处改动,请依次文字分析各个改动的具体内容与意义:
- RoPE
- RMSNorm
- GQA
- MoE
- SwiGLU
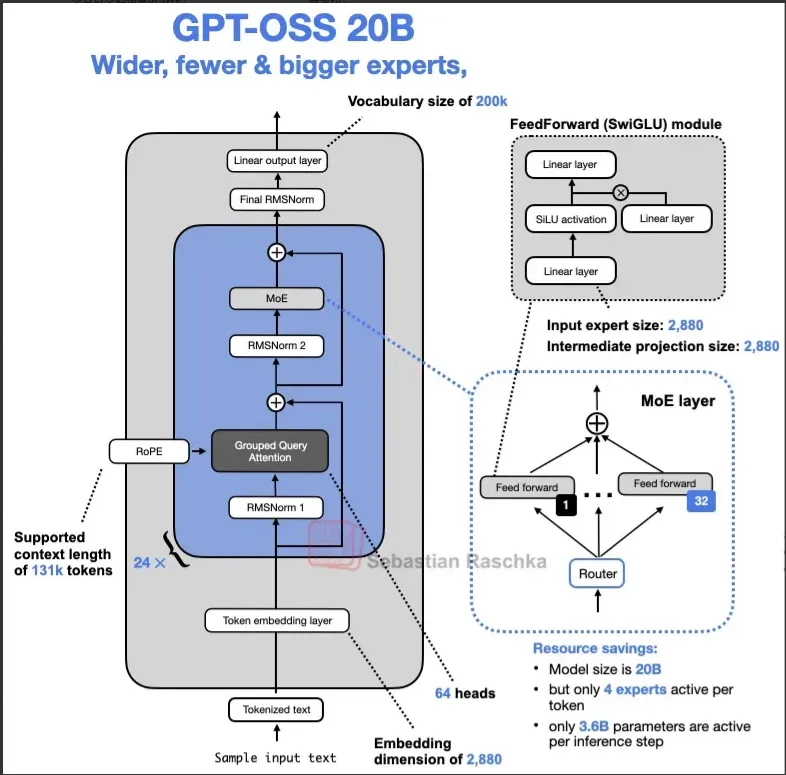
解:
- RoPE(Rotary Positional Embedding)替换位置编码Positional Embedding
- 问题:原始 Transformer 使用绝对位置编码
- 位置是"加到 embedding 上"的,而不是参与注意力计算
- 对超长上下文泛化能力差
- 对相对顺序建模不自然
- 优点:RoPE 将位置信息直接旋转到 Q / K 向量空间中,不再是 x + pos,而是 Q ′ = Q ⋅ R ( θ ) , K ′ = K ⋅ R ( θ ) Q' = Q \cdot R(\theta), \quad K' = K \cdot R(\theta) Q′=Q⋅R(θ),K′=K⋅R(θ),其中旋转角度与 token 的相对位置有关。
- 天然建模相对位置
- 长上下文泛化能力更强
- 与注意力机制深度耦合
- 问题:原始 Transformer 使用绝对位置编码
- RMSNorm替代LayerNorm
- 问题:LayerNorm 计算公式 LN ( x ) = x − μ σ \text{LN}(x) = \frac{x - \mu}{\sigma} LN(x)=σx−μ
- 需要计算均值 + 方差(代价大)
- 均值会破坏尺度信息
- 在大模型中数值不稳定
- RMSNorm 去掉均值,具体计算公式 RMSNorm ( x ) = x mean ( x 2 ) \text{RMSNorm}(x) = \frac{x}{\sqrt{\text{mean}(x^2)}} RMSNorm(x)=mean(x2) x
- 计算更快(少一次 reduce)
- 训练更稳定
- 保留向量方向,只缩放幅值
- 更适合 Pre-Norm Transformer RMSNorm + PreNorm 几乎是当前大模型默认配置
- 问题:LayerNorm 计算公式 LN ( x ) = x − μ σ \text{LN}(x) = \frac{x - \mu}{\sigma} LN(x)=σx−μ
- GQA(Grouped Query Attention)替换MHA(Multi-Head Attention)
- 问题:MHA存在的问题
- 每个 head 都有独立 Q / K / V
- K / V 在推理阶段占用大量显存
- 在长上下文下成本爆炸
- GQA的做法是多个 Query Head 共享一组 Key / Value,结构介于MHA(完全独立)和MQA(所有 head 共享 KV)之间
GQA的核心逻辑是因为 Key / Value 表示的是"被关注的内容",而 Query 表示的是"关注的视角",多个视角完全可以共享同一份"被看的东西"。- KV cache 显存大幅降低
- 长上下文推理成本显著下降
- 性能几乎不损失
- 问题:MHA存在的问题
- MoE(Mixture of Experts)替换单个FFN
- 标准的FFN问题
- 每个 token 都走同一个 FFN
- 参数利用率低
- 规模一大 → 计算直接爆炸
- 改成MoE FFN,使用路由器(Router)动态选择激活的专家(FFN),每个 token 只激活部分专家。
- 增加模型容量:总参数量大幅增加(20B 模型容量)
- 计算效率:每次前向只激活少量参数(实际激活 3.6B)
- 专家分工,在不同的方向表现更优
- 标准的FFN问题
- SwiGLU(替代 ReLU / GELU FFN)
- 问题: FFN ( x ) = W 2 ⋅ GELU ( W 1 x ) \text{FFN}(x) = W_2 \cdot \text{GELU}(W_1 x) FFN(x)=W2⋅GELU(W1x)
- 单通道
- 非线性表达能力有限
- SwiGLU 形式的形式 FFN ( x ) = W 2 ⋅ ( SiLU ( W 1 x ) ⊙ W 3 x ) \text{FFN}(x) = W_2 \cdot (\text{SiLU}(W_1 x) \odot W_3 x) FFN(x)=W2⋅(SiLU(W1x)⊙W3x)
- 门控机制
- 两个线性投影
- 一个作为 gate
- 表达能力显著增强,更好的梯度流,并且与前面的MoE相契合
- 问题: FFN ( x ) = W 2 ⋅ GELU ( W 1 x ) \text{FFN}(x) = W_2 \cdot \text{GELU}(W_1 x) FFN(x)=W2⋅GELU(W1x)
总结
| 组件 | 核心目标 |
|---|---|
| RoPE | 长上下文泛化 |
| RMSNorm | 稳定 + 高效 |
| GQA | 推理显存压缩 |
| MoE | 参数效率最大化 |
| SwiGLU | 专家表达能力 |
第22题:Roofline Model 分析
结合下列代码和结果,设 repeat=32 时,f 函数在 GPU 上执行时用于数据移动和计算的时间分别为 T m o v e T_{move} Tmove和 T c o m p T_{comp} Tcomp ,并假设此时恰处于 Memory 和计算的平衡点,依次分析:
- repeat=16 时,用于数据移动和计算的时间各是多少,此时 GPU 处于 Memory-bounded or Compute-bounded?
- repeat=64 时,用于数据移动和计算的时间各是多少,此时 GPU 处于 Memory-bounded or Compute-bounded?
python
def f(x: Tensor[N]):
for _ in range(repeat):
x = x * 2
return x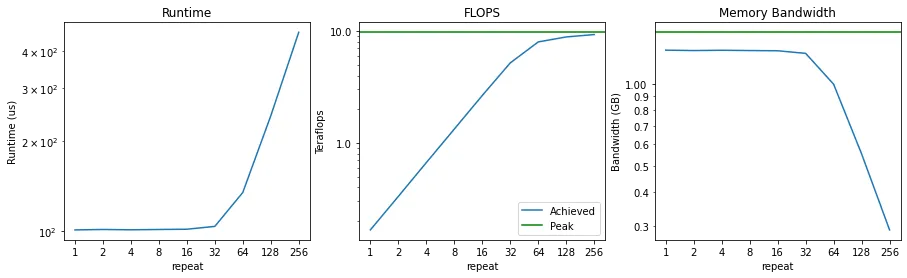
解:
- 由于 x x x只从显存加载一次、写回一次,与 repeat 无关,而计算时间与repeat成正相关
当repeat = 16时, T m o v e ( 16 ) = T m o v e ( 32 ) , T c o m p ( 16 ) = T c o m p ( 32 ) / 32 × 16 = 1 / 2 T c o m p ( 32 ) T_{move}(16)= T_{move}(32),\\T_{comp}(16) = T_{comp}(32)/32×16=1/2 T_{comp}(32) Tmove(16)=Tmove(32),Tcomp(16)=Tcomp(32)/32×16=1/2Tcomp(32)
此时处于Memory-bounded - 由于 x x x只从显存加载一次、写回一次,与 repeat 无关,而计算时间与repeat成正相关
当repeat = 64时, T m o v e ( 64 ) = T m o v e ( 32 ) , T c o m p ( 64 ) = T c o m p ( 32 ) / 32 × 64 = 2 T c o m p ( 32 ) T_{move}(64)= T_{move}(32),\\T_{comp}(64) = T_{comp}(32)/32×64=2 T_{comp}(32) Tmove(64)=Tmove(32),Tcomp(64)=Tcomp(32)/32×64=2Tcomp(32)
此时处于Compute-bounded
第23题:Operation Intensity 计算
GPU 的 Operation Intensity 定义为 浮点操作数 FLOPS 与 数据移动(Bytes)的比值,请计算并对比 LayerNorm 和 RMSNorm 的 Operation Intensity。
注意:d=8192,dtype=bf16,所有数据初始存于全局 DRAM,结果需写回全局 DRAM,且 SRAM 足够存放所有中间计算结果。
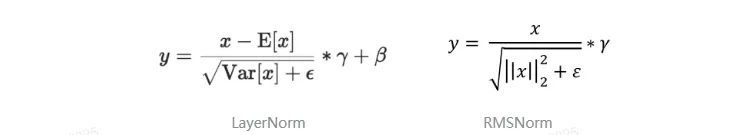
解:
Operation Intensity = Total FLOP Total Bytes Moved \text{Operation Intensity} = \frac{\text{Total FLOP}}{\text{Total Bytes Moved}} Operation Intensity=Total Bytes MovedTotal FLOP
对于LayerNorm: y = x − E [ x ] V a r [ x ] + ϵ ∗ γ + β y = \frac{x - E[x]}{\sqrt{Var[x] + \epsilon}} * \gamma + \beta y=Var[x]+ϵ x−E[x]∗γ+β
具体的FLOPS计算:
- 计算均值 ( E [ x ] E[x] E[x]):需要求和 ( d d d次加法)和1次除法。 ≈ d \approx d ≈dFLOPS
- 求方差 ( V a r [ x ] Var[x] Var[x]):减均值 x − E ( x ) x - E(x) x−E(x)( d d d次减法),平方的时候d次乘法,求和d次加法,1次除法 ≈ 3 d \approx 3d ≈3dFLOPS
- 归一化和缩放:标准化 ( ( x − E ( x ) ) × 1 V a r [ x ] + ϵ (x-E(x)) \times \frac{1}{\sqrt{Var[x]+\epsilon}} (x−E(x))×Var[x]+ϵ 1): d d d次乘法 (这里复用了第2步计算的 x − E ( x ) x-E(x) x−E(x)),缩放 ( × γ \times \gamma ×γ): d d d次乘法。平移 ( + β + \beta +β): d d d 次加法。 ≈ 3 d \approx 3d ≈3dFLOPS
LayerNorm 总 FLOPs: d + 3 d + 3 d = 7 d FLOPs d + 3d + 3d = 7d \text{FLOPs} d+3d+3d=7dFLOPs
DRAM 数据移动(Bytes)
- 输入向量 x x x: 1 × d 1 \times d 1×d 个元素
- 参数 γ \gamma γ: 1 × d 1 \times d 1×d 个元素
- 参数 β \beta β: 1 × d 1 \times d 1×d 个元素
- 输出向量 y y y: 1 × d 1 \times d 1×d 个元素
LayerNorm 总 Bytes = ( 3 d + 1 d ) × 2 Bytes/element = 8 d Bytes (3d + 1d) \times 2 \text{ Bytes/element} = \mathbf{8d \text{ Bytes}} (3d+1d)×2 Bytes/element=8d Bytes
LayerNorm Operation Intensity: O I L N = 7 d 8 d = 7 8 = 0.875 FLOP/Byte OI_{LN} = \frac{7d}{8d} = \frac{7}{8} = \mathbf{0.875 \text{ FLOP/Byte}} OILN=8d7d=87=0.875 FLOP/Byte
对于RMSNorm: y = x ∣ ∣ x ∣ ∣ 2 2 + ϵ ∗ γ y = \frac{x}{\sqrt{||x||_2^2 + \epsilon}} * \gamma y=∣∣x∣∣22+ϵ x∗γ
具体的FLOPS计算:
- 计算 RMS:平方 ( x 2 x^2 x2): d d d次乘法,求和: d d d次加法(开根号与除法忽略不计) ≈ 2 d \approx 2d ≈2d FLOPS
- 归一化和缩放:标准化 ( x × 1 ∣ ∣ x ∣ ∣ 2 2 + ϵ x \times \frac{1}{\sqrt{||x||_2^2 + \epsilon}} x×∣∣x∣∣22+ϵ 1): d d d 次乘法;缩放 ( × γ \times \gamma ×γ): d d d次乘法 = 2 d FLOPs = 2d\ \text{FLOPs} =2d FLOPs
RMSNorm 总 FLOPs: 2 d + 2 d = 4 d FLOPs 2d + 2d = 4d \ \text{FLOPs} 2d+2d=4d FLOPs
DRAM 数据移动(Bytes)
- 输入向量 x x x: 1 × d 1 \times d 1×d 个元素
- 参数 γ \gamma γ: 1 × d 1 \times d 1×d 个元素
- 输出向量 y y y: 1 × d 1 \times d 1×d 个元素
RMSNorm 总 Bytes = ( 2 d + 1 d ) × 2 Bytes/element = 6 d Bytes (2d + 1d) \times 2 \text{ Bytes/element} = \mathbf{6d \text{ Bytes}} (2d+1d)×2 Bytes/element=6d Bytes
RMSNorm Operation Intensity: O I R M S = 4 d 6 d = 2 3 ≈ 0.667 FLOP/Byte OI_{RMS} = \frac{4d}{6d} = \frac{2}{3} \approx \mathbf{0.667 \text{ FLOP/Byte}} OIRMS=6d4d=32≈0.667 FLOP/Byte
对比:LayerNorm 的 OI 为 0.875 FLOP/Byte,RMSNorm 的 OI 为 0.667 FLOP/Byte。两者都很低,属于 Memory-bounded 操作。RMSNorm 虽然计算量更少,但由于数据移动占主导,实际加速效果有限。
第24题:A100 Operation Intensity 分析
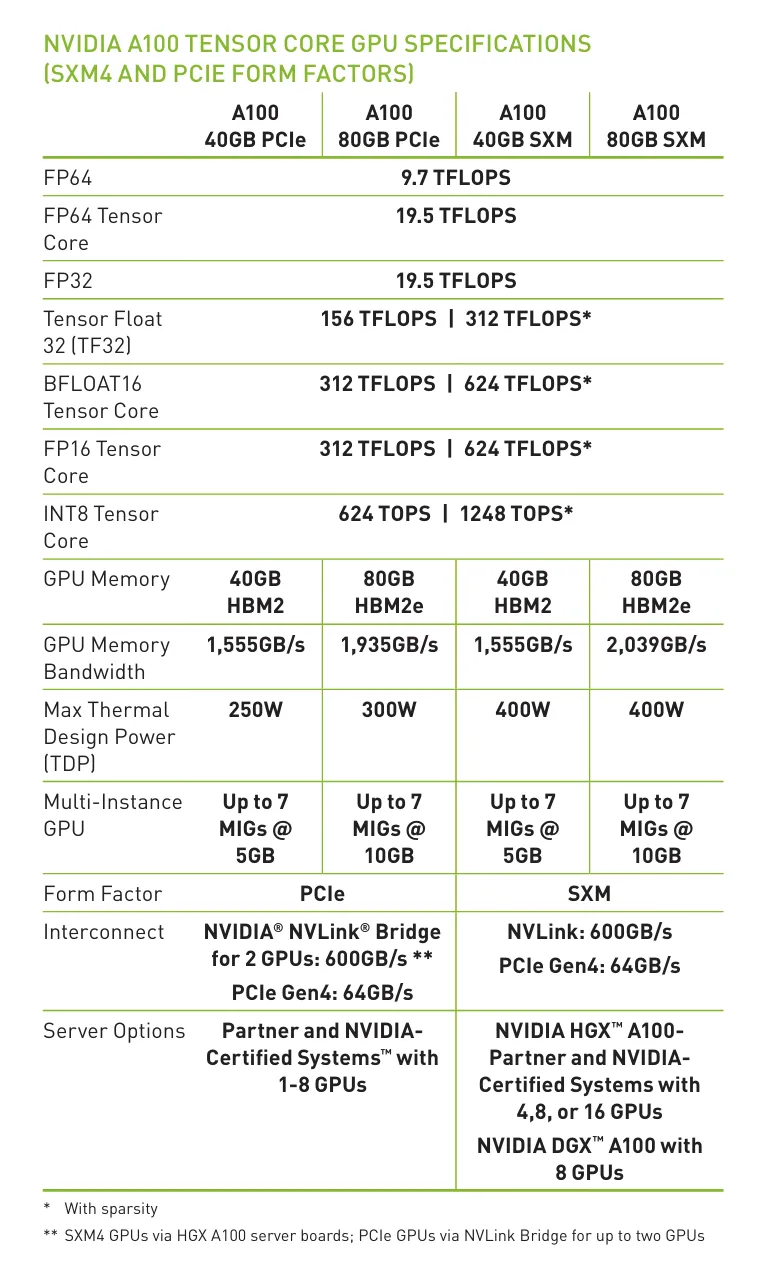
以 A100 为例,分析 FP32 和 BF16(TensorCore,考虑dense 即左边列的 FLOPS) 类型在进入 Compute-bounded 时需要的Operation Intensity 分别是多少。Bandwidth 统一简化为 2TB/s。
解:
由表可得:
FP32:19.5 TFLOPS
BF16(TensorCore):312 TFLOPS
Memory Bandwidth:2TB/s = 2000 GB/s
当计算时间等于数据传输时间时,达到平衡点:
Intensity FP32 = 19.5 TFLOPS 2 TB/s = 9.75 FLOP/Byte Intensity BF16 = 312 TFLOPS 2 TB/s = 156 FLOP/Byte \text{Intensity}{\text{FP32}} = \frac{19.5 \text{ TFLOPS}}{2 \text{ TB/s}} = 9.75 \text{ FLOP/Byte}\\ \text{Intensity}{\text{BF16}} = \frac{312 \text{ TFLOPS}}{2 \text{ TB/s}} = 156 \text{ FLOP/Byte} IntensityFP32=2 TB/s19.5 TFLOPS=9.75 FLOP/ByteIntensityBF16=2 TB/s312 TFLOPS=156 FLOP/Byte
- 要让 FP32 计算进入 Compute-bounded,Operation Intensity 需要 ≥ 9.75 FLOP/Byte
- 要让 BF16(TensorCore) 计算进入 Compute-bounded,Operation Intensity 需要 ≥ 156 FLOP/Byte