LeetCode 2943.最大化网格图中正方形空洞的面积：小小思维

【LetMeFly】2943.最大化网格图中正方形空洞的面积：小小思维

力扣题目链接：https://leetcode.cn/problems/maximize-area-of-square-hole-in-grid/

给你一个网格图，由 n + 2 条 横线段 和 m + 2 条 竖线段 组成，一开始所有区域均为 1 x 1 的单元格。

所有线段的编号从 1 开始。

给你两个整数 n 和 m 。

同时给你两个整数数组 hBars 和 vBars 。

hBars 包含区间 [2, n + 1] 内 互不相同 的横线段编号。
vBars 包含 [2, m + 1] 内 互不相同的 竖线段编号。

如果满足以下条件之一，你可以移除两个数组中的部分线段：

如果移除的是横线段，它必须是 hBars 中的值。
如果移除的是竖线段，它必须是 vBars 中的值。

请你返回移除一些线段后（可能不移除任何线段） ，剩余网格图中 最大正方形 空洞的面积，正方形空洞的意思是正方形内部不含有任何线段。

示例 1：

复制代码

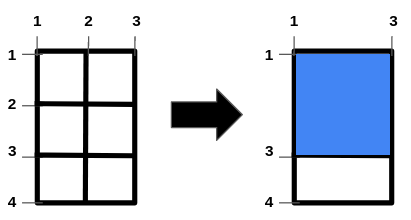
输入：n = 2, m = 1, hBars = [2,3], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2,3] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 2：

复制代码

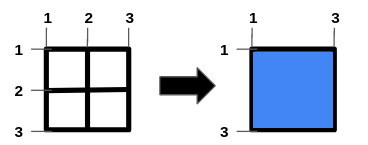
输入：n = 1, m = 1, hBars = [2], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,3] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 3：

复制代码

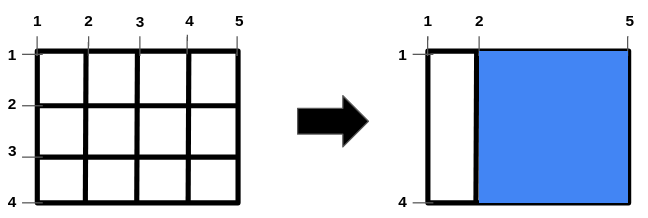
输入：n = 2, m = 3, hBars = [2,3], vBars = [2,3,4]
输出：9
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,5] 。
可以移除的横线段为 [2,3] ，竖线段为 [2,3,4] 。
一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。
操作后得到的网格图如右图所示。
正方形空洞面积为 9。
无法得到面积大于 9 的正方形空洞。
所以答案为 9 。

提示：

1 <= n <= 10⁹
1 <= m <= 10⁹
1 <= hBars.length <= 100
2 <= hBars[i] <= n + 1
1 <= vBars.length <= 100
2 <= vBars[i] <= m + 1
hBars 中的值互不相同。
vBars 中的值互不相同。

解题方法：最大连续

简单换个思维， m i n ( 水平方向移除一些线后的最大连续空格 , 竖直方向移除一些线后的最大连续空格 ) min(水平方向移除一些线后的最大连续空格, 竖直方向移除一些线后的最大连续空格) min(水平方向移除一些线后的最大连续空格,竖直方向移除一些线后的最大连续空格)即为正方形的最大边长。

水平方向移除一些线后的最大连续空格数是多少呢？很简单，把所有能移除的都移除呗。具体来说：

使用一个变量 l a s t last last记录当前空格向右处理到哪条线了，使用一个变量 c n t cnt cnt记录当前空格的连续长度。

遍历分隔线数组，如果当前能移除的分隔线正好等于 l a s t + 1 last+1 last+1，则空格可以继续网友拓展（更新 c n t + 1 cnt+1 cnt+1，更新 l a s t + 1 last+1 last+1）；

否则，说明上个连续空格无法拓展到这条线，更新答案最大值，并将 c n t cnt cnt初始化为 2 2 2（这条线可以移除，空格长度为2），更新last为当前这条线。

时间复杂度 O ( h log ⁡ h + v log ⁡ v ) O(h\log h+v\log v) O(hlogh+vlogv)，其中 h = l e n ( h B a r s ) h=len(hBars) h=len(hBars)， v = l e n ( v B a r s ) v=len(vBars) v=len(vBars)
空间复杂度 O ( log ⁡ h + log ⁡ v ) O(\log h+\log v) O(logh+logv)，时空复杂度的主要来源都是排序，因为题目没说给定分隔线有序。

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2026-01-15 10:20:39
 */
class Solution {
private:
    int getMaxDiff(vector<int>& v) {
        int last = 1, cnt = 1, ans = 1;
        for (int t : v) {
            if (t == last + 1) {
                cnt++;
                last++;
            } else {
                ans = max(ans, cnt);
                cnt = 2;
                last = t;
            }
        }
        ans = max(ans, cnt);
        return ans;
    }
public:
    int maximizeSquareHoleArea(int n, int m, vector<int>& hBars, vector<int>& vBars) {
        sort(hBars.begin(), hBars.end());
        sort(vBars.begin(), vBars.end());
        int side = min(getMaxDiff(hBars), getMaxDiff(vBars));
        return side * side;
    }

    int testGetMaxDiff(vector<int>& v) {
        return getMaxDiff(v);
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源