【ML】机器学习进阶

文章目录

- [第10题：Kernel Method分析](#第10题：Kernel Method分析)
- 第11题：超平面的函数间隔和几何间隔
- 第12题：SVM的Lagrange函数和对偶形式
- 第13题：线性不可分的SVM与L1正则
- 第14题：SVM最优化问题分析【SMO】
- 第15题：信息增益比计算
- 第16题：XGBoost损失函数二阶泰勒展开

第10题：Kernel Method分析

Kernel method 中，若 Kernel function K ( x , z ) = ( x ⊤ z + c ) 2 K(x, z) = (x^\top z + c)^2 K(x,z)=(x⊤z+c)2，推导对应的 feature mapping ϕ \phi ϕ，并讨论对于 n n n个样本一轮 SGD，使用 Kernel method 和在 feature map 上的计算效率优化比。提示：

基于 feature map 的参数更新方法为： θ : = θ + α ∑ i = 1 n ( y ( i ) − θ ⊤ ϕ ( x ( i ) ) ) ϕ ( x ( i ) ) \theta := \theta + \alpha \sum_{i=1}^n \big(y^{(i)} - \theta^\top \phi(x^{(i)}) \big) \phi(x^{(i)}) θ:=θ+α∑i=1n(y(i)−θ⊤ϕ(x(i)))ϕ(x(i))；
Kernel method 的参数更新方法为： θ : = θ + α ( y ⃗ − K θ ) \theta := \theta + \alpha(\vec{y} - K\theta) θ:=θ+α(y −Kθ)，其中 K j = K ( x ( i ) , x ( j ) ) K_{j} = K(x^{(i)}, x^{(j)}) Kj=K(x(i),x(j))。

解：

对于 x , z ∈ R d x, z \in \mathbb{R}^d x,z∈Rd，展开核函数：
K ( x , z ) = ( x ⊤ z + c ) 2 = ( x 1 z 1 + x 2 z 2 + ⋯ + x d z d + c ) 2 = ∑ i = 1 d x i 2 z i 2 + ∑ i ≠ j 2 x i x j z i z j + 2 c ∑ i = 1 d x i z i + c 2 \begin{aligned} K(x, z) &= (x^\top z + c)^2 \\ &= (x_1 z_1 + x_2 z_2 + \dots + x_d z_d + c)^2 \\ &=\sum_{i=1}^d x_i^2 z_i^2 + \sum_{i \neq j} 2x_i x_j z_i z_j + 2c \sum_{i=1}^d x_i z_i + c^2 \end{aligned} K(x,z)=(x⊤z+c)2=(x1z1+x2z2+⋯+xdzd+c)2=i=1∑dxi2zi2+i=j∑2xixjzizj+2ci=1∑dxizi+c2

因此，feature mapping 为：
为了找到 ϕ ( x ) \phi(x) ϕ(x)，需要把上面的每一项都拆解为"关于 x x x的部分"乘以"关于 z z z的部分"： x i 2 z i 2 = ( x i 2 ) ⋅ ( z i 2 ) x_i^2 z_i^2 = (x_i^2) \cdot (z_i^2) xi2zi2=(xi2)⋅(zi2)； 2 x i x j z i z j = ( 2 x i x j ) ⋅ ( 2 z i z j ) 2x_i x_j z_i z_j=(\sqrt{2}x_i x_j) \cdot (\sqrt{2}z_i z_j) 2xixjzizj=(2 xixj)⋅(2 zizj)； 2 c x i z i = ( 2 c x i ) ⋅ ( 2 c z i ) 2c x_i z_i = (\sqrt{2c} x_i) \cdot (\sqrt{2c} z_i) 2cxizi=(2c xi)⋅(2c zi)； c 2 = ( c ) ⋅ ( c ) c^2 = (c) \cdot (c) c2=(c)⋅(c)
ϕ ( x ) = ( x 1 2 , x 2 2 , ... , x d 2 , 2 x 1 x 2 , 2 x 1 x 3 , ... , 2 x d − 1 x d , 2 c x 1 , ... , 2 c x d , c ) \phi(x) = (x_1^2, x_2^2, \dots, x_d^2, \sqrt{2}x_1x_2, \sqrt{2}x_1x_3, \dots, \sqrt{2}x_{d-1}x_d, \sqrt{2c}x_1, \dots, \sqrt{2c}x_d, c) ϕ(x)=(x12,x22,...,xd2,2 x1x2,2 x1x3,...,2 xd−1xd,2c x1,...,2c xd,c)

维度为： D = d + ( d 2 ) + d + 1 = d + d ( d − 1 ) 2 + d + 1 = d ( d + 3 ) 2 + 1 = O ( d 2 ) D=d + \binom{d}{2} + d + 1 = d + \frac{d(d-1)}{2} + d + 1 = \frac{d(d+3)}{2} + 1 = O(d^2) D=d+(2d)+d+1=d+2d(d−1)+d+1=2d(d+3)+1=O(d2)

Feature map 方法： θ : = θ + α ∑ i = 1 n ( y ( i ) − θ ⊤ ϕ ( x ( i ) ) ) ϕ ( x ( i ) ) \theta := \theta + \alpha \sum_{i=1}^n \big(y^{(i)} - \theta^\top \phi(x^{(i)}) \big) \phi(x^{(i)}) θ:=θ+α∑i=1n(y(i)−θ⊤ϕ(x(i)))ϕ(x(i))
先将所有 x x x 映射到 D D D 维空间，然后在 D D D 维空间进行线性运算。
- 单次更新复杂度：计算内积 θ ⊤ ϕ ( x ( i ) ) \theta^\top \phi(x^{(i)}) θ⊤ϕ(x(i)) 需要 O ( D ) O(D) O(D)。
- n n n个样本一轮总复杂度： O ( n ⋅ D ) = O ( n ⋅ d 2 ) O(n \cdot D) = O(n \cdot d^2) O(n⋅D)=O(n⋅d2)。
- 总计： O ( n d 2 ) O(nd^2) O(nd2) 每轮 SGD
Kernel method： θ : = θ + α ( y ⃗ − K θ ) \theta := \theta + \alpha(\vec{y} - K\theta) θ:=θ+α(y −Kθ)，其中 K j = K ( x ( i ) , x ( j ) ) K_{j} = K(x^{(i)}, x^{(j)}) Kj=K(x(i),x(j))
核方法直接在低维空间 d d d 计算内积的平方，而不需要显式构造 ϕ ( x ) \phi(x) ϕ(x)。
- 单次更新复杂度：需要计算 n 2 n^2 n2 个元素，每个元素 K ( x ( i ) , x ( j ) ) K(x^{(i)}, x^{(j)}) K(x(i),x(j)) 在原空间计算只需 O ( d ) O(d) O(d)。总计 O ( n 2 d ) O(n^2d) O(n2d)。
- 更新步骤：矩阵与向量乘法 K θ K\theta Kθ 的复杂度为 O ( n 2 ) O(n^2) O(n2)。
- 总计： O ( n 2 d + n 2 ) = O ( n 2 d ) O(n^2 d + n^2) = O(n^2 d) O(n2d+n2)=O(n2d) 每轮 SGD

效率比
Feature map Kernel method = O ( n d 2 ) O ( n 2 d ) = d n \frac{\text{Feature map}}{\text{Kernel method}} = \frac{O(nd^2)}{O(n^2 d)} = \frac{d}{n} Kernel methodFeature map=O(n2d)O(nd2)=nd

当 n ≪ d n \ll d n≪d 时（样本少，特征多），Kernel method 更高效
当 n ≫ d n \gg d n≫d 时（样本多，特征少），Feature map 方法更高效

第11题：超平面的函数间隔和几何间隔

对超平面 w ⊤ x + b = 0 w^\top x + b=0 w⊤x+b=0，样本 x ( i ) x^{(i)} x(i)到的函数间隔 γ ^ ( i ) \hat{\gamma}^{(i)} γ^(i)与几何间隔 γ ( i ) \gamma^{(i)} γ(i)满足关系何种？直接给出答案即可。
解：

函数间隔定义为：
γ ^ ( i ) = y ( i ) ( w ⊤ x ( i ) + b ) \hat{\gamma}^{(i)} = y^{(i)} (w^\top x^{(i)} + b) γ^(i)=y(i)(w⊤x(i)+b)

几何间隔定义为：
γ ( i ) = y ( i ) ( w ⊤ x ( i ) + b ) ∣ w ∣ = γ ^ ( i ) ∣ w ∣ \gamma^{(i)} = \frac{y^{(i)} (w^\top x^{(i)} + b)}{|w|} = \frac{\hat{\gamma}^{(i)}}{|w|} γ(i)=∣w∣y(i)(w⊤x(i)+b)=∣w∣γ^(i)

关系：
γ ( i ) = γ ^ ( i ) ∣ w ∣ \gamma^{(i)} = \frac{\hat{\gamma}^{(i)}}{|w|} γ(i)=∣w∣γ^(i)

注：几何间隔是函数间隔除以权重向量的范数，表示点到超平面的真实距离。

第12题：SVM的Lagrange函数和对偶形式

已知 SVM 的优化目标为：
min ⁡ w , b 1 2 ∥ w ∥ 2 s.t. y ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 , i = 1 , ... , n \begin{aligned} \min_{w, b} & \ \ \frac{1}{2} \|w\|^2 \\ \text{s.t.} & \ \ y^{(i)}(w^\top x^{(i)} + b) \ge 1, \ i = 1, \dots, n \end{aligned} w,bmins.t. 21∥w∥2 y(i)(w⊤x(i)+b)≥1, i=1,...,n （1）

请构造其 Lagrange 函数 L ( w , b , α ) \mathcal{L}(w, b, \alpha) L(w,b,α)。

已知 L ( w , b , α ) \mathcal{L}(w, b, \alpha) L(w,b,α)满足 Slater 条件，因此强对偶成立，问题（1）最终可转化为 max ⁡ α : α i ≥ 0 min ⁡ w L ( w , b , α ) \max_{\alpha: \alpha_i \ge 0} \min_w \mathcal{L}(w, b, \alpha) maxα:αi≥0minwL(w,b,α)，证明该偶对形式问题可进一步转化为：
max ⁡ α W ( α ) = max ⁡ α ( ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n y ( i ) y ( j ) α i α j ⟨ x ( i ) , x ( j ) ⟩ ) s.t. α i ≥ 0 , i = 1 , ... , n ∑ i = 1 n α i y ( i ) = 0 \begin{aligned} \max_{\alpha} & \ \ W(\alpha) = \max_{\alpha} \Big( \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y^{(i)}y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle \Big) \\ \text{s.t.} & \ \ \alpha_i \ge 0, \ \ i = 1, \dots, n \\ & \ \ \sum_{i=1}^n \alpha_i y^{(i)} = 0 \end{aligned} αmaxs.t. W(α)=αmax(i=1∑nαi−21i,j=1∑ny(i)y(j)αiαj⟨x(i),x(j)⟩) αi≥0, i=1,...,n i=1∑nαiy(i)=0 （2）

提示：

首先在固定 α \alpha α下优化 w w w，得到 w w w关于 α \alpha α、 x ( i ) x^{(i)} x(i)、 y ( i ) y^{(i)} y(i)的关系；
类似优化 b b b，得到 α \alpha α与 y ( i ) y^{(i)} y(i)的关系；
将上述关系代入 L ( w , b , α ) \mathcal{L}(w, b, \alpha) L(w,b,α)。

解：
原始优化问题 (Primal Problem)

目标：在保证分类正确的前提下，最大化分类间隔。数学表达为：
min ⁡ w , b 1 2 ∥ w ∥ 2 \min_{w,b} \frac{1}{2} \|w\|^2 minw,b21∥w∥2
s.t. y ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 , i = 1 , ... , n \text{s.t. } y^{(i)}(w^\top x^{(i)} + b) \geq 1, \quad i = 1, \dots, n s.t. y(i)(w⊤x(i)+b)≥1,i=1,...,n
构造 Lagrange 函数:

引入拉格朗日乘子 α i ≥ 0 \alpha_i \geq 0 αi≥0，将约束条件合并到目标函数中：
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y ( i ) ( w ⊤ x ( i ) + b ) − 1 ] \mathcal{L}(w, b, \alpha) = \frac{1}{2}\|w\|^2 - \sum_{i=1}^{n} \alpha_i \left[ y^{(i)}(w^\top x^{(i)} + b) - 1 \right] L(w,b,α)=21∥w∥2−i=1∑nαi[y(i)(w⊤x(i)+b)−1]
求解极小值 (对 w w w 和 b b b 求导):
由于强对偶性成立（满足 Slater 条件），我们可以先求 L \mathcal{L} L 关于 w w w 和 b b b 的极小值。

对 w w w 求偏导：
∂ L ∂ w = w − ∑ i = 1 n α i y ( i ) x ( i ) = 0 ⟹ w = ∑ i = 1 n α i y ( i ) x ( i ) \frac{\partial \mathcal{L}}{\partial w} = w - \sum_{i=1}^{n} \alpha_i y^{(i)} x^{(i)} = 0 \implies w = \sum_{i=1}^{n} \alpha_i y^{(i)} x^{(i)} ∂w∂L=w−i=1∑nαiy(i)x(i)=0⟹w=i=1∑nαiy(i)x(i)

这说明最佳权重向量 w w w 是样本特征的线性组合

对 b b b 求偏导：
∂ L ∂ b = − ∑ i = 1 n α i y ( i ) = 0 ⟹ ∑ i = 1 n α i y ( i ) = 0 \frac{\partial \mathcal{L}}{\partial b} = -\sum_{i=1}^{n} \alpha_i y^{(i)} = 0 \implies\sum_{i=1}^{n} \alpha_i y^{(i)} = 0 ∂b∂L=−i=1∑nαiy(i)=0⟹i=1∑nαiy(i)=0

这是对偶问题的一个核心约束条件

将上述两个结论代入 L ( w , b , α ) \mathcal{L}(w, b, \alpha) L(w,b,α) 中，消除 w w w 和 b b b：
L = 1 2 w ⊤ w − ∑ i = 1 n α i y ( i ) w ⊤ x ( i ) − b ∑ i = 1 n α i y ( i ) + ∑ i = 1 n α i \mathcal{L} = \frac{1}{2} w^\top w - \sum_{i=1}^n \alpha_i y^{(i)} w^\top x^{(i)} - b \sum_{i=1}^n \alpha_i y^{(i)} + \sum_{i=1}^n \alpha_i L=21w⊤w−i=1∑nαiy(i)w⊤x(i)−bi=1∑nαiy(i)+i=1∑nαi

利用 b b b 的导数结论：
由于 ∑ α i y ( i ) = 0 \sum \alpha_i y^{(i)} = 0 ∑αiy(i)=0，所以含 b b b 的项直接消失。
利用 w w w 的导数结论：
将 w = ∑ α i y ( i ) x ( i ) w = \sum \alpha_i y^{(i)} x^{(i)} w=∑αiy(i)x(i) 代入前两项，经过内积运算简化为：
L = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y ( i ) y ( j ) ⟨ x ( i ) , x ( j ) ⟩ \mathcal{L} = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n \alpha_i \alpha_j y^{(i)} y^{(j)} \langle x^{(i)}, x^{(j)} \rangle L=i=1∑nαi−21i,j=1∑nαiαjy(i)y(j)⟨x(i),x(j)⟩ ⟨ x ( i ) , x ( j ) ⟩ = ( x ( i ) ) ⊤ x ( j ) = ∑ k = 1 n x k ( i ) x k ( j ) \langle x^{(i)}, x^{(j)} \rangle = (x^{(i)})^\top x^{(j)} = \sum_{k=1}^{n} x^{(i)}_k x^{(j)}_k ⟨x(i),x(j)⟩=(x(i))⊤x(j)=∑k=1nxk(i)xk(j)

现在问题转化为了只关于 α \alpha α 的极大值问题：
max ⁡ α W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n α i α j y ( i ) y ( j ) ⟨ x ( i ) , x ( j ) ⟩ \max_{\alpha} W(\alpha) = \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i,j=1}^{n} \alpha_i \alpha_j y^{(i)} y^{(j)} \langle x^{(i)}, x^{(j)} \rangle maxαW(α)=∑i=1nαi−21∑i,j=1nαiαjy(i)y(j)⟨x(i),x(j)⟩

s.t.
α i ≥ 0 , i = 1 , ... , n \alpha_i \geq 0, \quad i = 1, \dots, n αi≥0,i=1,...,n
∑ i = 1 n α i y ( i ) = 0 \sum_{i=1}^{n} \alpha_i y^{(i)} = 0 ∑i=1nαiy(i)=0 由 ∂ L ∂ b = 0 \frac{\partial \mathcal{L}}{\partial b}=0 ∂b∂L=0可得

第13题：线性不可分的SVM与L1正则

对于线性不可分的训练集，SVM 对应带 L1 正则的优化目标是什么？已知对线性可分几何的优化为：
min ⁡ w , b 1 2 ∥ w ∥ 2 s.t. y ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 , i = 1 , ... , n \begin{aligned} \min_{w, b} & \ \ \frac{1}{2} \|w\|^2 \\ \text{s.t.} & \ \ y^{(i)}(w^\top x^{(i)} + b) \ge 1, \ i = 1, \dots, n \end{aligned} w,bmins.t. 21∥w∥2 y(i)(w⊤x(i)+b)≥1, i=1,...,n （1）

解：

对于线性不可分的情况，引入松弛变量 ξ i ≥ 0 \xi_i \geq 0 ξi≥0，允许某些样本违反间隔约束。
带 L1 正则的软间隔 SVM 优化目标
min ⁡ w , b , ξ 1 2 ∣ w ∣ 2 + C ∑ i = 1 n ξ i \min_{w,b,\xi} \frac{1}{2}|w|^2 + C \sum_{i=1}^{n} \xi_i minw,b,ξ21∣w∣2+C∑i=1nξi

s.t.

y ( i ) ( w ⊤ x ( i ) + b ) ≥ 1 − ξ i , i = 1 , ... , n y^{(i)}(w^\top x^{(i)} + b) \geq 1 - \xi_i, \quad i = 1, \dots, n y(i)(w⊤x(i)+b)≥1−ξi,i=1,...,n
ξ i ≥ 0 , i = 1 , ... , n \xi_i \geq 0, \quad i = 1, \dots, n ξi≥0,i=1,...,n

参数含义

ξ i \xi_i ξi：松弛变量，表示样本 i i i 违反间隔的程度。
C > 0 C > 0 C>0：惩罚参数，控制间隔最大化与违反程度之间的权衡。
C ∑ i = 1 n ξ i C \sum_{i=1}^n \xi_i C∑i=1nξi：L1 正则项，是对松弛变量的惩罚。

总结

该目标函数平衡了两个目标：

最大化间隔（通过最小化 ∣ w ∣ 2 |w|^2 ∣w∣2）。
最小化分类错误（通过最小化 ∑ ξ i \sum \xi_i ∑ξi）。

第14题：SVM最优化问题分析【SMO】

已知 SVM 的最终优化目标为： W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n y ( i ) y ( j ) α i α j ⟨ x ( i ) , x ( j ) ⟩ W(\alpha) = \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i,j=1}^n y^{(i)}y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle W(α)=∑i=1nαi−21∑i,j=1ny(i)y(j)αiαj⟨x(i),x(j)⟩。假设此时正在优化 α 1 \alpha_1 α1与 α 2 \alpha_2 α2，并有 α 1 = ( ζ − α 2 y ( 2 ) ) y ( 1 ) \alpha_1 = (\zeta - \alpha_2 y^{(2)})y^{(1)} α1=(ζ−α2y(2))y(1)。请推导此时 α 2 \alpha_2 α2应当更新的值。

在讨论 α 2 \alpha_2 α2的可取范围时，可直接使用下图中的 H H H/ L L L/ C C C。

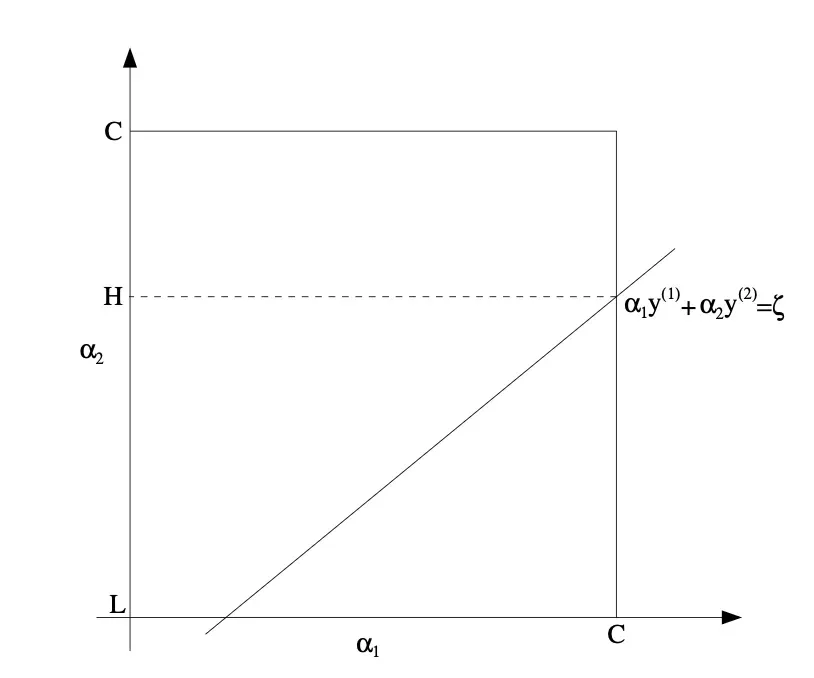
SMO（Sequential Minimal Optimization）是一种用来高效训练 SVM 的算法，它把一个很难解的大规模二次规划问题，拆成很多"只更新两个变量"的小问题来解。

解：
对于题目进行回顾

SVM 对偶目标函数为
W ( α ) = ∑ i = 1 n α i − 1 2 ∑ i , j = 1 n y ( i ) y ( j ) α i α j ⟨ x ( i ) , x ( j ) ⟩ W(\boldsymbol{\alpha})= \sum_{i=1}^n \alpha_i-\frac{1}{2}\sum_{i,j=1}^n y^{(i)}y^{(j)}\alpha_i\alpha_j \langle x^{(i)},x^{(j)}\rangle W(α)=i=1∑nαi−21i,j=1∑ny(i)y(j)αiαj⟨x(i),x(j)⟩

现在只优化 α 1 \alpha_1 α1和 α 2 \alpha_2 α2，其余 α \alpha α固定，则约束条件：
∑ i α i y ( i ) = 0 ⇒ α 1 y ( 1 ) + α 2 y ( 2 ) = ζ \sum_i \alpha_i y^{(i)} = 0 \quad\Rightarrow\quad \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta ∑iαiy(i)=0⇒α1y(1)+α2y(2)=ζ得到 α 1 = ( ζ − α 2 y ( 2 ) ) y ( 1 ) \alpha_1 = (\zeta - \alpha_2 y^{(2)})y^{(1)} α1=(ζ−α2y(2))y(1)
将目标函数进行简化

在固定其他 α i ( i ≥ 3 ) \alpha_i(i\ge3) αi(i≥3)情况下，目标函数关于 α 1 \alpha_1 α1， α 2 \alpha_2 α2可以简化为
对于 α 1 2 K 11 \alpha_1^2 K_{11} α12K11为什么没有显示乘以 ( y ( i ) ) 2 = 1 (y^{(i)})^2 = 1 (y(i))2=1，
why：在 SVM 中，标签 y ( i ) y^{(i)} y(i)的取值只能是 + 1 +1 +1或 − 1 -1 −1，所以 ( y ( i ) ) 2 = 1 (y^{(i)})^2 = 1 (y(i))2=1。
W ( α 1 , α 2 ) = α 1 + α 2 − 1 2 ( α 1 2 K 11 + α 2 2 K 22 + 2 y ( 1 ) y ( 2 ) α 1 α 2 K 12 ) + const W(\alpha_1,\alpha_2)= \alpha_1 + \alpha_2-\frac{1}{2}\Big( \alpha_1^2 K_{11}+\alpha_2^2K_{22}+2 y^{(1)}y^{(2)}\alpha_1\alpha_2 K_{12} \Big)+\text{const} W(α1,α2)=α1+α2−21(α12K11+α22K22+2y(1)y(2)α1α2K12)+const

其中 K i j = ⟨ x ( i ) , x ( j ) ⟩ K_{ij}=\langle x^{(i)},x^{(j)}\rangle Kij=⟨x(i),x(j)⟩

将约束 α 1 = ( ζ − α 2 y ( 2 ) ) y ( 1 ) \alpha_1 = (\zeta - \alpha_2 y^{(2)}) y^{(1)} α1=(ζ−α2y(2))y(1)带入目标函数 W ( α 1 , α 2 ) W(\alpha_1,\alpha_2) W(α1,α2)
W ( α 2 ) = − 1 2 η α 2 2 + α 2 [ 1 − y ( 2 ) ( E 2 − E 1 ) ] + const W(\alpha_2)=-\frac{1}{2}\eta\alpha_2^2+\alpha_2 \Big[ 1-y^{(2)}(E_2 - E_1) \Big]+\text{const} W(α2)=−21ηα22+α2[1−y(2)(E2−E1)]+const

其中 η = K 11 + K 22 − 2 K 12 \eta = K_{11} + K_{22} - 2K_{12} η=K11+K22−2K12（特征空间距离）, E i = f ( x ( i ) ) − y ( i ) E_i = f(x^{(i)}) - y^{(i)} Ei=f(x(i))−y(i)（预测误差）

对于 α 2 \alpha_2 α2求极值，求导并令其为0
d W d α 2 = − η α 2 + [ 1 − y ( 2 ) ( E 2 − E 1 ) ] = 0 \frac{dW}{d\alpha_2} = -\eta \alpha_2+\big[1 - y^{(2)}(E_2 - E_1)\big] = 0 dα2dW=−ηα2+[1−y(2)(E2−E1)]=0

得到未裁剪的更新值： α 2 unc = α 2 old + y ( 2 ) ( E 1 − E 2 ) η \alpha_2^{\text{unc}}=\alpha_2^{\text{old}}+\frac{y^{(2)}(E_1 - E_2)}{\eta} α2unc=α2old+ηy(2)(E1−E2)

考虑约束条件，由图可知

0 ≤ α 1 ≤ C 0 \le \alpha_1 \le C 0≤α1≤C
0 ≤ α 2 ≤ C 0 \le \alpha_2 \le C 0≤α2≤C
α 1 y ( 1 ) + α 2 y ( 2 ) = ζ \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta α1y(1)+α2y(2)=ζ

由此可得 α 2 \alpha_2 α2的上下界:

若 y ( 1 ) ≠ y ( 2 ) y^{(1)} \neq y^{(2)} y(1)=y(2)： L = max ⁡ ( 0 , α 2 o l d − α 1 o l d ) ， H = min ⁡ ( C , C + α 2 o l d − α 1 o l d ) L = \max(0, \alpha_2^{old} - \alpha_1^{old}) ，H = \min(C, C + \alpha_2^{old} - \alpha_1^{old}) L=max(0,α2old−α1old)，H=min(C,C+α2old−α1old)
若 y ( 1 ) = y ( 2 ) y^{(1)} = y^{(2)} y(1)=y(2)： L = max ⁡ ( 0 , α 2 o l d + α 1 o l d − C ) ， H = min ⁡ ( C , α 2 o l d + α 1 o l d ) L = \max(0, \alpha_2^{old} +\alpha_1^{old}-C) ，H = \min(C, \alpha_2^{old} + \alpha_1^{old}) L=max(0,α2old+α1old−C)，H=min(C,α2old+α1old)

最终更新公式：
α 2 new = { H , if α 2 new > H α 2 new , if L ≤ α 2 new ≤ H L , if α 2 new < L \alpha_2^{\text{new}} = \begin{cases} H, & \text{if } \alpha_2^{\text{new}} > H \\ \alpha_2^{\text{new}}, & \text{if } L \leq \alpha_2^{\text{new}} \leq H \\ L, & \text{if } \alpha_2^{\text{new}} < L \end{cases} α2new=⎩ ⎨ ⎧H,α2new,L,if α2new>Hif L≤α2new≤Hif α2new<L

通过约束更新 α 1 \alpha_1 α1得到：
α 1 new = ( ζ − α 2 new y ( 2 ) ) y ( 1 ) α 1 new = α 1 old + y ( 1 ) y ( 2 ) ( α 2 old − α 2 new ) \alpha_1^{\text{new}}=(\zeta - \alpha_2^{\text{new}} y^{(2)}) y^{(1)}\\\alpha_1^{\text{new}}=\alpha_1^{\text{old}}+y^{(1)}y^{(2)}(\alpha_2^{\text{old}}-\alpha_2^{\text{new}}) α1new=(ζ−α2newy(2))y(1)α1new=α1old+y(1)y(2)(α2old−α2new)

更新前： α 1 old y ( 1 ) + α 2 old y ( 2 ) = ζ \alpha_1^{\text{old}} y^{(1)}+\alpha_2^{\text{old}} y^{(2)}=\zeta α1oldy(1)+α2oldy(2)=ζ
更新后也必须满足： α 1 new y ( 1 ) + α 2 new y ( 2 ) = ζ \alpha_1^{\text{new}} y^{(1)}+\alpha_2^{\text{new}} y^{(2)}=\zeta α1newy(1)+α2newy(2)=ζ
两式相减： ( α 1 new − α 1 old ) y ( 1 ) + ( α 2 new − α 2 old ) y ( 2 ) = 0 (\alpha_1^{\text{new}}-\alpha_1^{\text{old}})y^{(1)}+(\alpha_2^{\text{new}}-\alpha_2^{\text{old}})y^{(2)} =0 (α1new−α1old)y(1)+(α2new−α2old)y(2)=0

old：更新前的值；unc：忽略边界时的理论最优值；new：把unc裁剪到 [ L , H ] [L,H] [L,H]后的最终值；C 是全局给定的上限， L / H L/H L/H是在本次更新中由约束推出来的区间端点。 C C C是SVM 给定的超参数，控制"允许违反间隔的程度" L L L是 α 2 \alpha_2 α2能取到的最小值, H H H是 α 2 \alpha_2 α2能取到的最大值

第15题：信息增益比计算

计算下图中，四个特征的信息增益比。可保留 log 项，统一底数为 2。

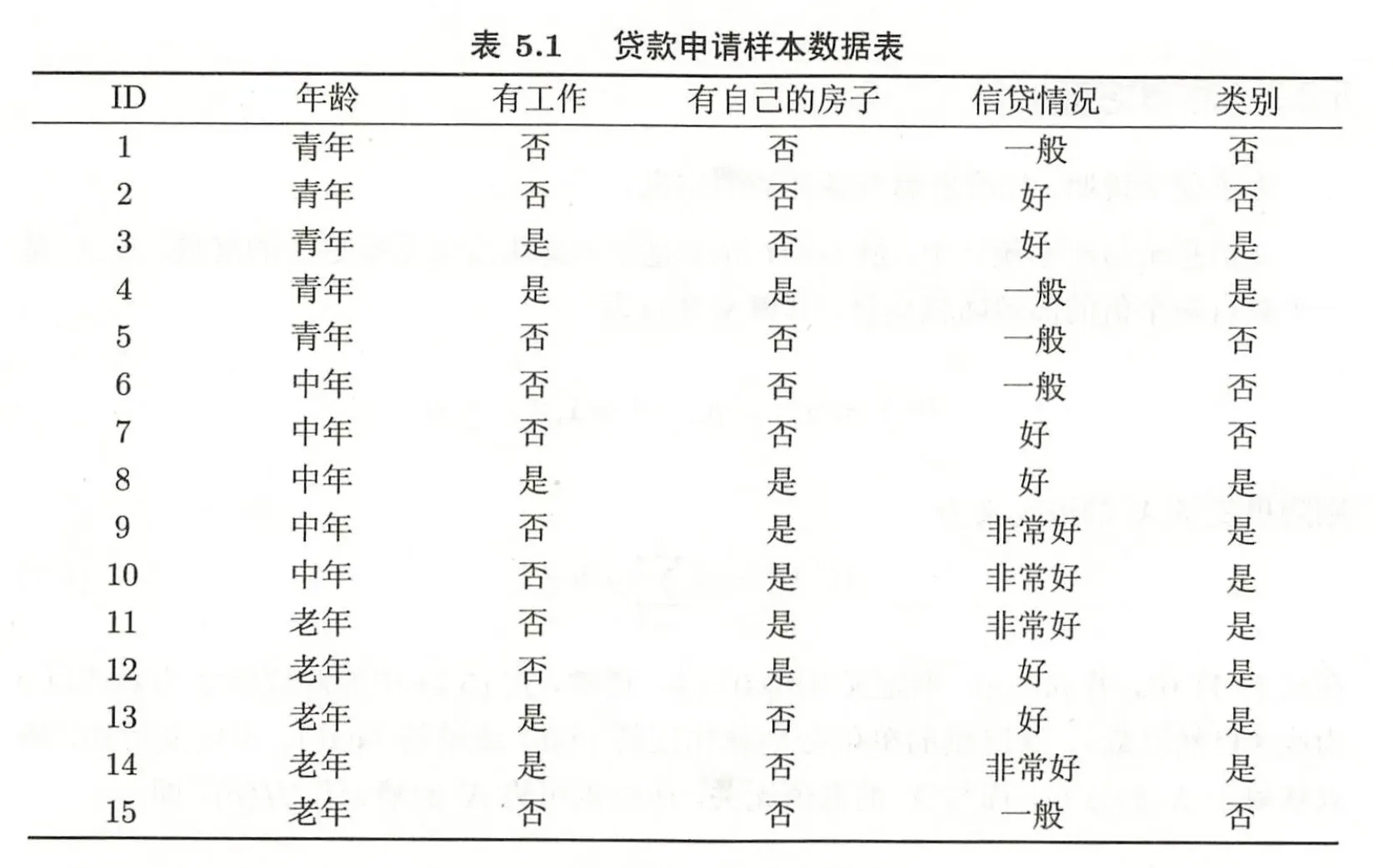
熵（Entropy）： H ( D ) = − ∑ c ∈ C l a s s e s p ( c ) log ⁡ 2 p ( c ) H(D) = -\sum_{c \in Classes} p(c) \log_2 p(c) H(D)=−∑c∈Classesp(c)log2p(c)

信息增益： IG ( A ) = H ( D ) − ∑ v ∈ V a l u e s ( A ) ∣ D v ∣ ∣ D ∣ H ( D v ) \text{IG}(A) = H(D) - \sum_{v \in Values(A)} \frac{|D_v|}{|D|} H(D_v) IG(A)=H(D)−∑v∈Values(A)∣D∣∣Dv∣H(Dv)

分裂信息（Split Information）： SI ( A ) = − ∑ v ∈ V a l u e s ( A ) ∣ D v ∣ ∣ D ∣ log ⁡ 2 ( ∣ D v ∣ ∣ D ∣ ) \text{SI}(A) = -\sum_{v \in Values(A)} \frac{|D_v|}{|D|} \log_2 \left( \frac{|D_v|}{|D|} \right) SI(A)=−∑v∈Values(A)∣D∣∣Dv∣log2(∣D∣∣Dv∣)

信息增益比 G a i n R a t i o = IG ( A ) SI ( A ) GainRatio = \frac{\text{IG}(A) }{\text{SI}(A)} GainRatio=SI(A)IG(A)

解：

第16题：XGBoost损失函数二阶泰勒展开

已知 XGBoost 优化第 t 棵数时的损失函数为：
L ( t ) = ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) + γ T + 1 2 λ ∑ t = 1 T w j 2 \mathcal{L}^{(t)} = \sum_{i=1}^n l(y_i, \hat{y}i^{(t-1)} + f_t(x_i)) + \gamma T + \frac{1}{2}\lambda \sum{t=1}^T w_j^2 L(t)=∑i=1nl(yi,y^i(t−1)+ft(xi))+γT+21λ∑t=1Twj2

请推导 l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) l(yi,y^i(t−1)+ft(xi))在 l ( y i , y ^ i ( t − 1 ) ) l(y_i, \hat{y}_i^{(t-1)}) l(yi,y^i(t−1))处对于 f t ( x i ) f_t(x_i) ft(xi)的二阶泰勒展开。其中，一阶和二阶导数可使用：
g i = ∂ l ( y i , y ^ i ) ∂ y ^ i ∣ y ^ i ( t − 1 ) g_i = \frac{\partial l(y_i, \hat{y}_i)}{\partial \hat{y}i} \vert{\hat{y}_i^{(t-1)}} gi=∂y^i∂l(yi,y^i)∣y^i(t−1), h i = ∂ 2 l ( y i , y ^ i ) ∂ y ^ i 2 ∣ y ^ i ( t − 1 ) h_i = \frac{\partial^2 l(y_i, \hat{y}_i)}{\partial \hat{y}i^2} \vert{\hat{y}_i^{(t-1)}} hi=∂y^i2∂2l(yi,y^i)∣y^i(t−1)

在此基础上，推导叶子节点 j j j对应的 w j ∗ w_j^* wj∗满足：
w j ∗ = − ∑ i ∈ I j g i ∑ i ∈ I j h i + λ w_j^*=-\frac{\sum_{i \in \mathcal{I}j} g_i}{\sum{i \in \mathcal{I}_j} h_i + \lambda} wj∗=−∑i∈Ijhi+λ∑i∈Ijgi

其中， I j = { i ∣ q ( x i ) = j } \mathcal{I}_j=\{i \mid q(x_i)=j\} Ij={i∣q(xi)=j}表示属于叶子节点 j j j的样本集合。

解：

二阶泰勒展开
泰勒通式： f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x + 1 2 f ′ ′ ( x ) Δ x 2 f(x + \Delta x) \approx f(x) + f'(x)\Delta x + \frac{1}{2}f''(x)\Delta x^2 f(x+Δx)≈f(x)+f′(x)Δx+21f′′(x)Δx2
x x x对应上一步的预测值 y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y^i(t−1)；
Δ x \Delta x Δx对应当前步要学习的增量 f t ( x i ) f_t(x_i) ft(xi)

在 y ^ i ( t − 1 ) \hat{y}_i^{(t-1)} y^i(t−1) 处对 l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) l(yi,y^i(t−1)+ft(xi)) 关于 f t ( x i ) f_t(x_i) ft(xi) 进行二阶泰勒展开：
l ( y i , y ^ i ( t − 1 ) + f t ( x i ) ) ≈ l ( y i , y ^ i ( t − 1 ) ) + ∂ l ( y i , y ^ i ) ∂ y ^ i ∣ y ^ i ( t − 1 ) f t ( x i ) + 1 2 ∂ 2 l ( y i , y ^ i ) ∂ y ^ i 2 ∣ y ^ i ( t − 1 ) f t ( x i ) 2 = l ( y i , y ^ i ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t ( x i ) 2 \begin{aligned} l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) &\approx l(y_i, \hat{y}_i^{(t-1)}) \quad + \frac{\partial l(y_i, \hat{y}_i)}{\partial \hat{y}i} \bigg|{\hat{y}_i^{(t-1)}} f_t(x_i) \quad + \frac{1}{2} \frac{\partial^2 l(y_i, \hat{y}_i)}{\partial \hat{y}i^2} \bigg|{\hat{y}_i^{(t-1)}} f_t(x_i)^2 \\ &= l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2 \end{aligned} l(yi,y^i(t−1)+ft(xi))≈l(yi,y^i(t−1))+∂y^i∂l(yi,y^i) y^i(t−1)ft(xi)+21∂y^i2∂2l(yi,y^i) y^i(t−1)ft(xi)2=l(yi,y^i(t−1))+gift(xi)+21hift(xi)2

因此损失函数变为：
L ( t ) ≈ ∑ i = 1 n [ l ( y i , y ^ i ( t − 1 ) ) + g i f t ( x i ) + 1 2 h i f t ( x i ) 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 \mathcal{L}^{(t)} \approx \sum_{i=1}^n [l(y_i, \hat{y}i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2] + \gamma T + \frac{1}{2} \lambda \sum{j=1}^T w_j^2 L(t)≈i=1∑n[l(yi,y^i(t−1))+gift(xi)+21hift(xi)2]+γT+21λj=1∑Twj2

去掉常数项 ∑ i = 1 n l ( y i , y ^ i ( t − 1 ) ) \sum_{i=1}^n l(y_i, \hat{y}i^{(t-1)}) ∑i=1nl(yi,y^i(t−1))：
L ~ ( t ) = ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t ( x i ) 2 ] + γ T + 1 2 λ ∑ j = 1 T w j 2 \tilde{\mathcal{L}}^{(t)} = \sum{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t(x_i)^2] + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^T w_j^2 L~(t)=i=1∑n[gift(xi)+21hift(xi)2]+γT+21λj=1∑Twj2

推导叶子权重 w j ∗ w_j^* wj∗

对于树模型， f t ( x i ) = w q ( x i ) f_t(x_i) = w_{q(x_i)} ft(xi)=wq(xi)，其中 q ( x i ) q(x_i) q(xi) 表示样本 i i i 落在的叶子节点。

将样本按叶子节点分组：
L ~ ( t ) = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \tilde{\mathcal{L}}^{(t)} = \sum_{j=1}^T \left[ \left( \sum_{i \in \mathcal{I}j} g_i \right) w_j + \frac{1}{2} \left( \sum{i \in \mathcal{I}_j} h_i + \lambda \right) w_j^2 \right] + \gamma T L~(t)=j=1∑T i∈Ij∑gi wj+21 i∈Ij∑hi+λ wj2 +γT

记 G j = ∑ i ∈ I j g i G_j = \sum_{i \in \mathcal{I}j} g_i Gj=∑i∈Ijgi， H j = ∑ i ∈ I j h i H_j = \sum{i \in \mathcal{I}j} h_i Hj=∑i∈Ijhi，则：
L ~ ( t ) = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T \tilde{\mathcal{L}}^{(t)} = \sum{j=1}^T \left[ G_j w_j + \frac{1}{2} (H_j + \lambda) w_j^2 \right] + \gamma T L~(t)=j=1∑T[Gjwj+21(Hj+λ)wj2]+γT

对 w j w_j wj 求导并令其为 0：
对于每一个相互独立的叶子节点 j j j，我们需要找到使 L ~ ( t ) \tilde{\mathcal{L}}^{(t)} L~(t) 最小的 w j w_j wj。这是一个简单的二次函数求极值问题：对 w j w_j wj 求导并令其等于 0
∂ L ~ ( t ) ∂ w j = G j + ( H j + λ ) w j = 0 \frac{\partial \tilde{\mathcal{L}}^{(t)}}{\partial w_j} = G_j + (H_j + \lambda) w_j = 0 ∂wj∂L~(t)=Gj+(Hj+λ)wj=0

解得：
w j ∗ = − G j H j + λ = − ∑ i ∈ I j g i ∑ i ∈ I j h i + λ w_j^* = -\frac{G_j}{H_j + \lambda} = -\frac{\sum_{i \in \mathcal{I}j} g_i}{\sum{i \in \mathcal{I}_j} h_i + \lambda} wj∗=−Hj+λGj=−∑i∈Ijhi+λ∑i∈Ijgi