Python训练打卡Day5离散特征的处理-独热编码

在机器学习中，特征（Feature） 是描述数据的属性或变量，是模型用来学习和预测的基础。例如，在房价预测数据集中，特征可能包括房屋面积、房间数量、地理位置等。

根据特征的性质，可以将其分为 离散特征 和 连续特征。

---

离散特征**（Discrete Feature）**

离散特征是取值为有限个 或可数个的特征，通常是分类或计数数据。

示例：

• 二值特征：性别（男/女）、是否下雨（是/否）。
• 多类别特征：颜色（红/绿/蓝）、城市（北京/上海/广州）。
• 计数特征：家庭成员数量（1, 2, 3, ...）、订单数量。

处理方式：

• 独热编码（One-Hot Encoding）：将离散特征转换为二进制向量。
  • 例如，颜色（红/绿/蓝）可以编码为 [1, 0, 0], [0, 1, 0], [0, 0, 1]。
• 标签编码（Label Encoding）：将离散特征映射为整数。
  • 例如，颜色（红/绿/蓝）可以编码为 0, 1, 2。
• 嵌入（Embedding）：对于高基数离散特征（如用户ID），可以使用嵌入层将其映射到低维空间。

---

连续特征**（Continuous Feature）**

连续特征是取值为无限个的特征，通常是数值型数据，可以在某个范围内取任意值

示例：

• 物理量：身高（170.5 cm）、体重（65.3 kg）。
• 经济指标：房价（350000.5 元）、收入（50000.0 元）。

处理方式：

• 标准化（Standardization）：将特征转换为均值为 0、标准差为 1 的分布。
  • 公式：
• 归一化（Normalization）：将特征缩放到固定范围（如 [0, 1]）。
  • 公式：
• 分桶（Binning）：将连续特征离散化为多个区间。
  • 例如，将年龄分为 [0-18, 19-35, 36-60, 60+]。

---

任务: 一次性处理data数据中所有的连续变量和离散变量

处理逻辑：读取数据 → 拆分特征类型（离散/连续） → 对离散/连续处理缺失值（离散特征用众数填充，连续特征用均值填充） → 离散特征独热编码 → 最终验证

1.读取数据

import warnings
import pandas as pd

warnings.filterwarnings('ignore')  # 忽略警告信息（可选）

# 1. 读取数据 
data = pd.read_csv(r'data.csv')
print("原始数据形状：", data.shape)

2.找到所有的离散特征和连续特征

找到所有的离散特征（仅通过object区分）

# 找到离散变量
discrete_lists = [] # 新建一个空列表，用于存放离散变量名
for discrete_features in data.columns:
    if data[discrete_features].dtype == 'object':
      discrete_lists.append(discrete_features)

简化写法

discrete_cols = data.select_dtypes(include=['object']).columns.tolist() #离散特征
continuous_cols = [col for col in data.columns if col not in discrete_cols] #连续特征

3.分别处理缺失值

# 3. 分类型处理缺失值
data_filled = data.copy() #拷贝原数据，防止对原数据修改

# 3.1 离散特征：众数填充
for col in discrete_cols:
    null_count = data_filled[col].isnull().sum()
    if null_count > 0:
        mode_val = data_filled[col].mode()[0]  # 取第一个众数，可能存在多个数出现频次最高
        data_filled[col] = data_filled[col].fillna(mode_val)

# 3.2 连续特征：均值填充
for col in continuous_cols:
    null_count = data_filled[col].isnull().sum()
    if null_count > 0:
        mean_val = data_filled[col].mean()
        data_filled[col] = data_filled[col].fillna(mean_val)

4.离散特征独热编码

查看下离散特征数据分别情况

# value_counts()方法用于统计每个类别的个数，并返回一个Series对象。
# 这个方法可以帮助我们快速了解数据集中每个类别的分布情况。 
data['Home Ownership'].value_counts()

输出结果：

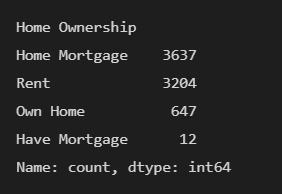
1. Home Ownership：房屋所有权
2. Rent：租房
3. Own Home：拥有自有住房
4. Have Mortgage：有抵押贷款

可以发现并不具备顺序关系，因此可以采用one-hot编码

我们这里对所有的离散特征都采用的独热编码，在实际中需要结合数据特征选择合适的编码方式

# 4. 独热编码（仅离散特征）
data_encoded = pd.get_dummies(
    data_filled,
    columns=discrete_cols,
    drop_first=True  # 避免多重共线性
)

pandas.get_dummies 是 pandas 库中专门用于生成独热编码的函数，核心是将离散特征的每个类别转换为二进制列（0/1）

核心参数

参数	作用	示例
data	待编码的 DataFrame/Series	pd.get_dummies(df['性别'])
columns	指定要编码的列（仅 DataFrame 需要）	pd.get_dummies(df, columns=['性别', '城市'])
dummy_na	是否将 NaN 作为独立类别	dummy_na=True → 缺失值单独成列
drop_first	是否删除第一列（避免多重共线性）	drop_first=True → 性别仅保留「女」列（男 = 0，女 = 1）
prefix	编码列的前缀（方便识别）	prefix='性别' → 列名变成「性别_男」「性别_女」

找到编码后新增的列

# 找到编码后新增的列
original_columns = data.columns.tolist()  #原始的特征列
new_cols = [col for col in data_encoded.columns if col not in original_columns]

# 将独热编码后生成的bool值转换为数值型，方便后续计算
data_encoded[new_cols] = data_encoded[new_cols].astype(int)

5.最后检验

# 5. 最终验证 
null_final = data_encoded.isnull().sum()
print(null_final[null_final > 0] if null_final[null_final > 0].any() else "无缺失值")

null_final[null_final > 0] if null_final[null_final > 0].any() else "无缺失值" 这是一个三元表达式。

三元表达式格式：结果1 if 条件 else 结果2

如果「条件」成立，执行「结果 1」；否则执行「结果 2」。

null_final[null_final > 0] 筛选出「缺失值数量 > 0」的列

完整代码示例：

import warnings
import pandas as pd

warnings.filterwarnings('ignore')  

#  1. 读取数据 + 备份原始信息 
data = pd.read_csv(r'data.csv')
original_columns = data.columns.tolist() # 原始列信息
print("原始数据形状：", data.shape)

# 2. 拆分离散/连续特征 
# 离散特征列表
discrete_cols = data.select_dtypes(include=['object']).columns.tolist()
# 连续特征列表（剩余列）
continuous_cols = [col for col in data.columns if col not in discrete_cols]


print("\n离散特征：", discrete_cols)
print("连续特征：", continuous_cols)

#  3. 分类处理缺失值 
data_filled = data.copy()  # 避免修改原始数据

# 3.1 处理离散特征缺失值：填充为众数
for col in discrete_cols:
    null_count = data_filled[col].isnull().sum()
    if null_count > 0:
        mode_val = data_filled[col].mode()[0] # 计算众数（处理多众数情况）
        data_filled[col] = data_filled[col].fillna(mode_val)

# 3.2 处理连续特征缺失值：填充为均值
for col in continuous_cols:
    null_count = data_filled[col].isnull().sum()
    if null_count > 0:
        mean_val = data_filled[col].mean()
        data_filled[col] = data_filled[col].fillna(mean_val)

# 4. 独热编码
data_encoded = pd.get_dummies(
    data_filled,
    columns=discrete_cols,
    drop_first=True  # 避免多重共线性
)

# 找到编码后新增的列
new_cols = [col for col in data_encoded.columns if col not in original_columns]
print(f"\n独热编码新增特征数：{len(new_cols)}")
print("新增特征名：", new_cols[:5] if len(new_cols) > 5 else new_cols)  # 只显示前5个

# 类型转换
if new_cols:
    data_encoded[new_cols] = data_encoded[new_cols].astype(int)

# 5. 最终验证 
null_final = data_encoded.isnull().sum()
print(null_final[null_final > 0] if null_final[null_final > 0].any() else "无缺失值")

【拓展】判断离散特征

一个特征能被判定为「离散特征」，需要满足两个条件：

1. 浮点数大概率不是离散特征 ； 且它不是整数形浮点数
2. 它值的数量≤设定的阈值（threshold）（即取值是有限个）。

条件1说明：有些浮点数列本质是离散值（比如 1.0、2.0、3.0，实际是「学历编号 1/2/3」，在统计数据的时候为了简洁，用数字表示学历 专科、本科、研究生）。对于整数形浮点数，就需要再进行条件2判断

条件2说明：threshold是人为设定一个标准，根据根据业务实际需求调整

def is_discrete(series, threshold=10):
    """判断是否为离散特征：唯一值少，且非浮点数（避免连续值）"""
    # 第一步：排除真正的连续浮点数
    if series.dtype == 'float' and not series.is_integer().all():
        return False
    # 第二步：低基数判断（核心）
    return series.nunique() <= threshold

# 离散特征列表
discrete_cols = [col for col in data.columns if is_discrete(data[col])]

@浙大疏锦行