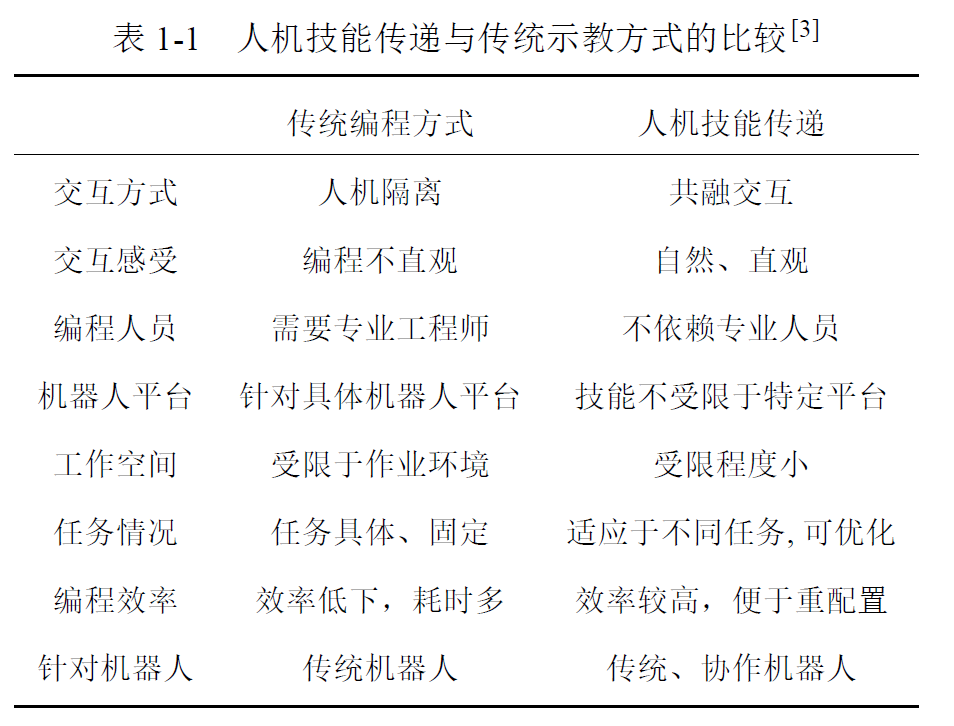
一、研究的背景
(1)从产品需求方面,传统工业产品品种单一,大批量,生产周期长。随着生产力的发展,催生新的市场需求:品种多样化,生产周期短,批量较小,具有个性化。
**(2)从制造模式上,**从传统的刚性生产模式转向柔性生产模式。
因此,传统工业机器人采用固化编程的方式不利于新需求下提高企业生产效率,因此需要柔顺的示教学习。构建人在回路的人-信息-机器人系统。
简单来说,示教学习就是将人的技能通过较少的示范数据的形式让机器人快速学习获得,从而让非专业人员也能实现机器人的个性化任务编程。
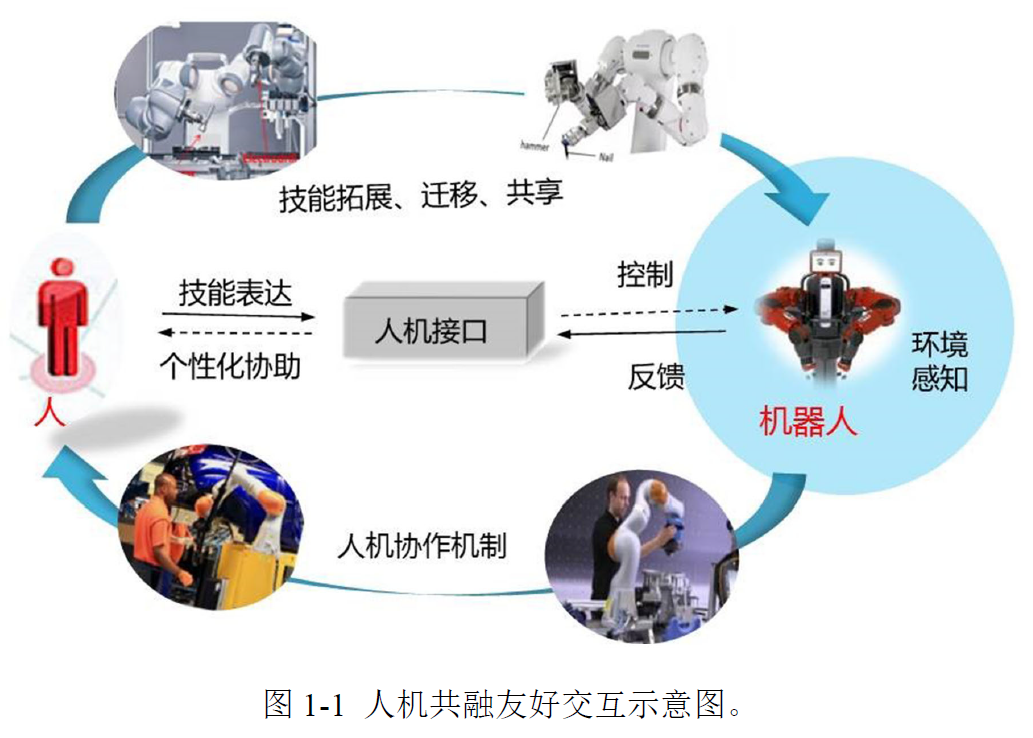
二、示教学习流程
示教学习一般分为三个阶段:(1)对机器人示教;(2)对示教数据建模;(3)机器人技能复现
(1)示教阶段: 在此阶段需要完成人对机器人的示教,即示教者充当"教师"角色,而相应地机器
人充当"学生"角色。示教者通过一定的人机交互方式对机器人进行任务示范,获取在某项任务中人的技能信息。
**(2)模型学习阶段:**对在示教阶段获取的数据进行建模,并从中学习相关技能信息。本质上是一个监督学习过程,即利用示教数据估计出所选模型的参数。一旦模型参数得以确定,则某一技能的表达(Representation) 也就确定了。此外,在此阶段还往往需要考虑其他的问题,如示教数据的对齐(Alignment)、轨迹(技能)分割(Segmentation)、技能的泛化(Generalization) 等
**(3)任务复现阶段:**在学习到技能特征之后,就可以把学习到的运动控制策略(即模型的输出)映射到相应的机器人关节或末端控制器中,继而使得机器人可以复现出所示教的技能,甚至是对所学习到的技能进行泛化以满足新的任务要求。
三、示教学习的人机交互方式
示教学习在采集示范数据阶段,需要通过一定的人机交互方式完成对机器人的示教任务,常见的示教方式包括以下三种:
(1)基于视觉(Vision-based) 的示教方式;
(2)基于遥操作(Teleoperation-based) 的示教方式;
(3)基于物理交互(Physical interaction) 的示教方式。

(1)基于视觉的示教方式: 在这种示教方式下,通过相机捕捉人在完成示教任务过程的中运动信息。例如,利用微软公司开发的Kinect 相机捕获示教者在运动中的手臂骨骼信息继而计算出手臂的关机角度,可将人的关节角度映射到机械臂的关节角度用于控制其运动以完成某项任务,如图1-3(a) 所示。再例如,如图1-3(b) 所示,可利用定位光标(Optical marker) 捕获示教者手臂末端的运动轨迹并将其传递给机械臂的末端,用于完成插孔任务。另外,还可以利用视频演示的方式实现对机器人的运动示教,即机器人通过"观看"视频来学习新的技能。基于视觉的示教方式的优点是人在示教过程肢体的运动不会受到机器的限制,缺点是往往因为缺乏反馈使得示教者感受不到机器人的运动,从而导致人机交互不够自然。

图1-4 (a)基于遥操作方式的示教
(2)基于遥操作的示教方式: 在这种示教方式下,人通过遥操作设备(如SIGMA 遥操作杆)远程控制机器人完成任务,其基本原理是通过遥操作设备将人的运动信息传递给机械臂,使得机械臂得
以跟随示教者运动,如图1-4(a) 所示。而往往遥操作设备与机械臂具有不同的机械结构,因此通常需要将两者的工作空间匹配起来。目前,基于遥操作的示教方式在手术机器人系统中应用比较广泛,其中较为著名的是达芬奇手术机器人。这种方式的优点是传递实现对机器人的远程操控,可以应用在如对核电设备的检修等场合。其缺点是遥操作系统中有时存在系统延时、震颤等问题需要解决。这里放一个遥操作项目链接

图1-4 (b)基于物理交互方式的示教
(3)基于物理交互的示教方式: 在这种示教方式下,示教者与机器人直接物理接触在机器人的示教模式下牵引机器人完成某项任务。如图1-4(b) 所示,示教者直接牵引KUKA 机器人的末端打开一个门把手。这种示教方式主要针对的是新型的协作机器人,一方面原因是这类机器人会向用户提供示教模式以方便对其完成示教;另一方面原因是这类机器人为人与机器人共同协作而设计,因而可以相对保证人机交互的安全性。在这种示教方式下人与机器人有直接的力的交互,因而可以增强人机交互的浸入感。其缺点是示教者与机器人近距离接触,导致人的运动受到一定限制。
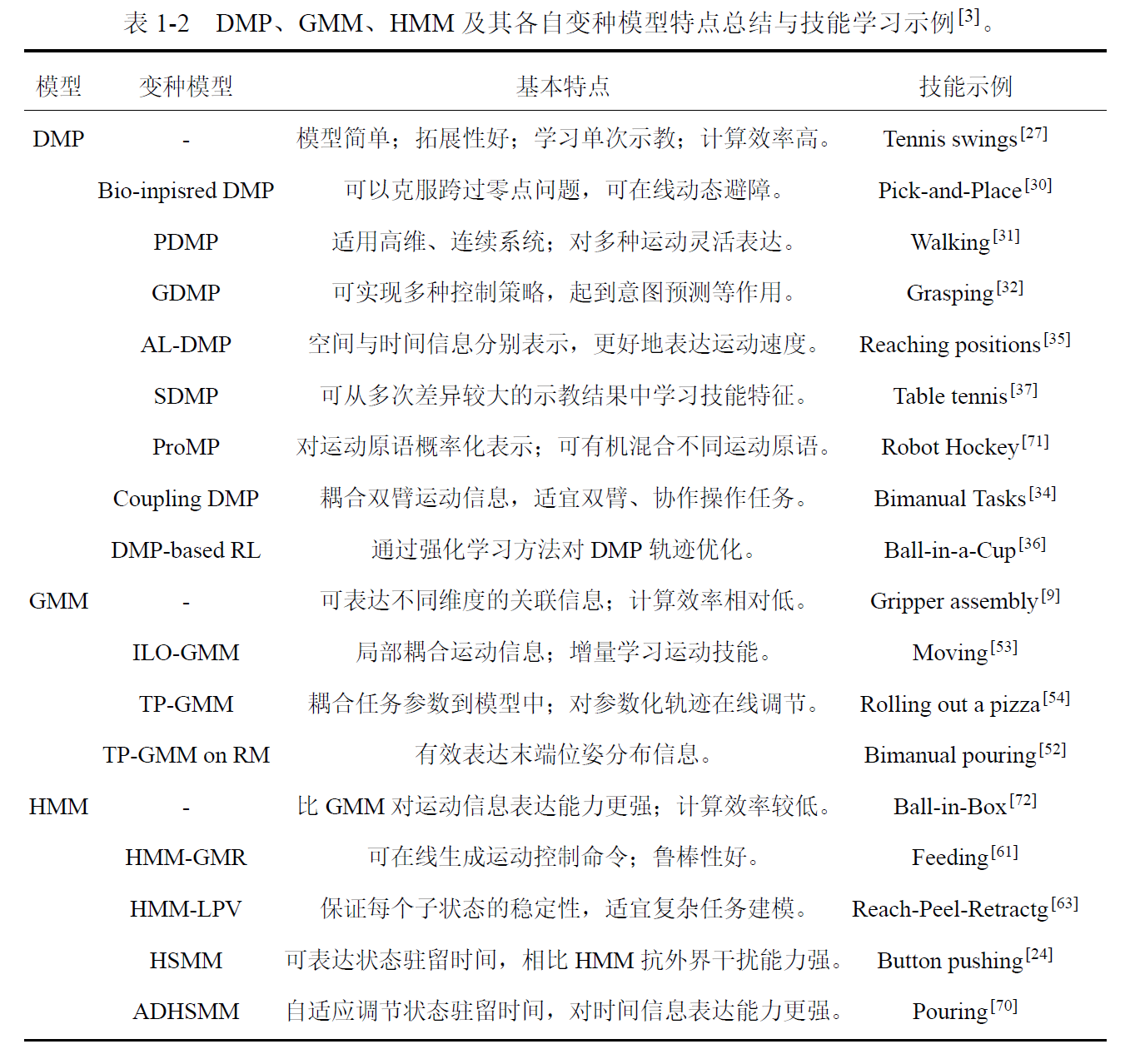
四、运动技能表达模型综述
在示教学习过程中,运动技能表达模型用于对人/机器人技能的运动轨迹进行通用性描述。一般地,可以用一系列简单的子系统加权求和来表示一条较为复杂运动轨迹,即:
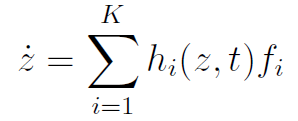
其中。
表示可以表征某项技能的特征变量,如运动位置、刚度、力等信息;
表示某一系统的子系统,该系统由参数
和
确定;
则表示相应的加权系数。
我们在整个示教学习过程,最主要的问题就是确定子系统的参数和
以及加权系数
。 常用的技能表达模型有动态运动原语(Dynamical movement primitives, DMPs) 和基于概率的模型 ,基于概率的模型包括以下三种,分别是高斯混合模型(Gaussian mixture model, GMM) ,隐马尔可夫模型(Hidden Markov model, HMM) 以及**隐半马尔可夫模型(Hidden semi-Markov model, HSMM)**等。下面分别对其进行叙述。
4.1 基于动态运动原语的技能表达
**什么是动态运动原语模型?**动态运动原语模型实质上是用一个二阶的非线性系统(弹簧-阻尼系统)来近似拟合一条运动轨迹。论文[26,27] 提出了动态原语模型用于机器人的示教技能学习。
**动态运动原语模型怎么分类?**通常按照运动类型不同,可以将一般的运动分为点到点(Point-to-point) 离散型运动和周期的节律型(Rhythmic) 运动。相应地,有两种DMP 模型即离散型DMP 和节律型DMP 分别用于这两种运动的技能表达。例如,一般的Pick-and-place 任务就是典型的离散型运动;而有节拍地敲打一件乐器是节律性运动。因而需要提前根据任务类型选择合适的DMP模型,一般情况下离散型DMP 的应用任务场合相对较多。
**动态原语模型优点是什么?**首先,DMP 模型非常简单,可以利用回归算法快速学习,因而可用于机器人在线轨迹规划。该模型便于轨迹拓展,仅作简单的参数调整即可得到一系列形状相似而目标值不同的运动轨迹,因而十分方便于任务的泛化。另外,DMP 模型的稳定性和鲁棒性很好,可以根据任务的需要在模型中添加不同的耦合项。例如,通过对DMP 模型中的非线性函数项进行参数化表示,即可把DMP 模型的学习变成一个优化问题,继而可用强化学习算法对DMP 的输出轨迹进行调整。
最近几年有哪些改进版本DMP?
文献[28]结合DMP模型提出了"查询子"的概念。该方法不仅考虑从示教数据中学习到的运动控制策略(即原DMP模型参数),还考虑了机器人在任务复现过程中的实时任务参数。通过引入查询子,能够将已学习好的DMP模型与当前任务状态动态关联。当任务状态发生变化时,可便捷地对模型参数进行选择或调整,从而实现技能的有效泛化。作者将该方法应用于机器人击打乐器任务,如图1-5(a)所示。

文献[29]针对机器人学习人类乒乓球技能提出了一种改进的DMP模型,如图1-5(b)所示。由于乒乓球任务具有高度复杂性,每一次击球时球的状态(如入射角度、飞行速度等)均难以提前确定,一般模型难以覆盖所有可能情形。该模型采用门控网络,从一组运动原语库中动态选择合适的运动原语,并通过有效组合这些原语,形成适应新任务情境的运动策略。
文献[30]对原始DMP模型的变换系统进行了改进。原始DMP模型仅对机器人运动技能本身进行建模,未引入环境信息。例如,在执行"抓取-放置"任务时,若目标物体的位置发生变化,原始模型无法感知这一变化,从而导致任务失败。改进后的变换系统将外部环境中任务相关物体(如目标或障碍物)的位置信息实时耦合到DMP模型中,使机器人能够动态感知环境状态,从而实现对运动轨迹的在线调整与动态避障。
文献[31]提出了一种参数化动态运动原语模型。该模型借鉴了人体手臂运动中的肌肉协同现象,即执行特定任务时不同肌肉的活动呈现出相似或一致的模式。例如,在抓取物体时,各手指的运动具有较高的协调性。PDMP将这种协同机制引入模型,通过对DMP中径向基函数进行参数化建模,使不同运动原语能够共享部分参数,从而降低了参数学习的复杂度,并提升了任务泛化能力。
文献[32]将DMP的参数学习问题转化为带约束的非线性最小二乘优化问题,并引入模型预测机制。机器人在执行任务时,可将当前运动状态作为约束条件,使模型实时生成对应的控制策略,实现运动意图预测、动态避障等功能。该方法在机械手抓取实验中得到了验证。
文献[33]通过重构经典DMP模型,将环境感知模块直接耦合到机器人的技能学习系统中。该设计使机器人能够在线获取环境反馈信息,从而实现对任务状态的提前判断与自适应调整。
在机器人示教过程中,示教者往往难以精确控制运动速度,过快或过大的速度会影响机器人对任务的复现效果。针对这一问题,文献[35]提出了基于弧长参数的动态运动原语模型。该方法对DMP中的参数进行弧长化处理,将示教技能中的位置信息与速度信息进行解耦表达,从而有效缓解了示教轨迹中速度波动过大的问题。
文献[34]则针对双臂协同技能学习,提出了一种新的DMP框架。该框架包含两个相互耦合的DMP模型,分别对应左臂和右臂的运动建模。通过在两套变换系统中引入一组互为反作用的虚拟力,使得一只机械臂的运动状态可被另一只实时感知,从而实现对双臂协同运动的自然耦合与协调控制。该文将该方法应用于机器人双臂协作任务中,具体如图1-6所示。

从多次不同的示教数据中学习也是人机技能传递研究领域中需要解决的问题。单次示教往往不足以获得较好的示教效果,也难以学习出好的机器人运动控制策略。为了能够从多次示教轨迹中学习技能信息,文献[38] 利用联合概率分布密度函数联合表示DMP 模型中的相位变量与变换系统中的非线性项。每一次示教轨迹对应一个非线性项,而所有不同次的示教对应共同的相位变量,进而可利用该概率分布函数得到一个包含不同示教信息的非线性项,DMP 模型的最终输出也是从不同示教数据中学习到的结果。
文献[39] 提出了风格化动态原语模型(Stylistic dynamical movement primitives, SDMP) 用于从多次示教中学习。该模型可以将不同次示教、不同示教者的运动风格信息耦合到DMP 模型中,因而能描述风格多样的运动轨迹,即使多次示教的轨迹在形状上存在较大差异。
如前文所述,可以利用强化学习算法对DMP 模型进行优化以满足任务要求。一般流程是:首先人对机器人示教得到示教数据;根据示教数据学习DMP 模型;在技能复现阶段,把学习到的DMP 参数作为强化学习算法的初始策略,根据任务要求定义适合的代价函数对DMP 模型参数进行优化直到完成任务。其中,有几种比较典型的基于DMP 模型的强化学习算法。文献[36,40] 提出了一种带回报权重搜索策略学习算法(Policylearning by weighting exploration with the returns,PoWER),用于DMP 模型的参数调节与优化;并将感知单元作为外部环境变量耦合到DMP 模型各个自由度的变换系统中。在任务复现阶段,PoWER 算法同时对表示环境的参数进行优化,可降低试错的次数。该算法在机器人接球实验中得到了验证,如图1-7(a) 所示。
文献[41,42] 提出了一种用于DMP 模型参数的基于路径积分的策略优化强化学习算法(Policy improvement with pathintegrals, PI2),该算法适用于对高维空间的连续运动轨迹的优化,并可以用于对机械臂各关节空间的刚度优化。文献[43] 将这种强化学习算法应用到了移动机器人的手臂协同抓取任务中,对高维度(机械臂与机械手)的运动轨迹同时进行优化,直到顺利完成抓取任务。文献[37] 将PI2 算法应用到了机器人序列运动的学习中,如图1-7(b) 所示。通过同时优化运动原语的形状参数与目标参数,使得机器人能够顺畅地完成序列化的任务。文献[44] 把对DMP 模型的调节看作是一个黑箱的优化问题,提出了进化策略算(Evolution Strategies,ES) 用于对DMP 模型的参数优化。文献[45] 进一步将ES 算法应用到了基于刚度调节的机器人抓取任务中。
4.2 基于概率模型的技能表达
4.2.1 高斯混合模型
基于概率的技能表达模型主要包括高斯混合模型与隐(半)马尔可夫模型。高斯混合模型可用参数来表示:
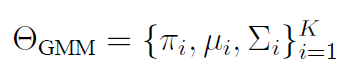
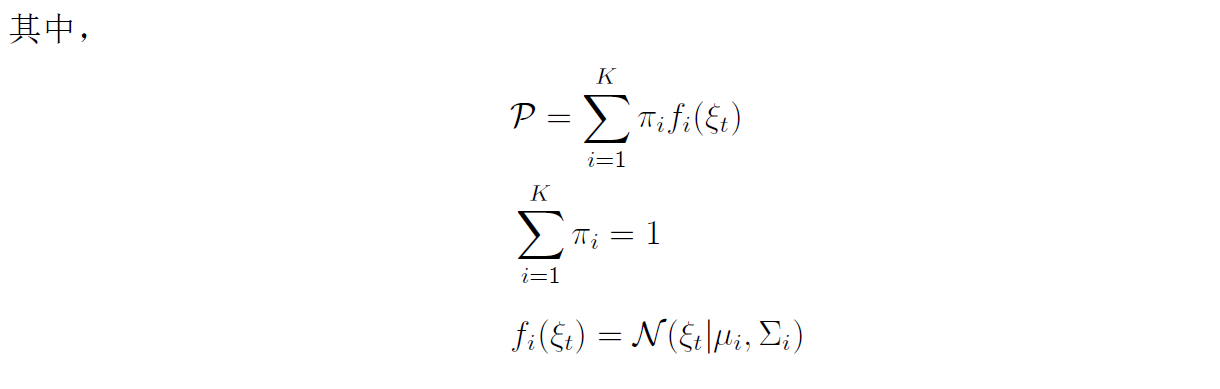
式中,代表教阶段收集的数据; 表示概率密度函数; 表示每个高斯组分的系数,满足,且所有系数之和为 1;表示条件概率密度函数,通常表示为高斯分布。
一般可用 EM 算法 (Expectation-Maximization) 估计出高斯混合模型的参数。在参数确定之后,即可利用高斯混合回归 (Gaussian mixture regression, GMR) 算法计算得到理想的运动策略 ,即。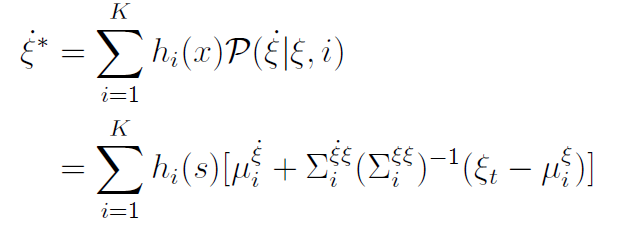
式中, 表示归一化的权重系数
4.2.2 (半)隐马尔可夫模型
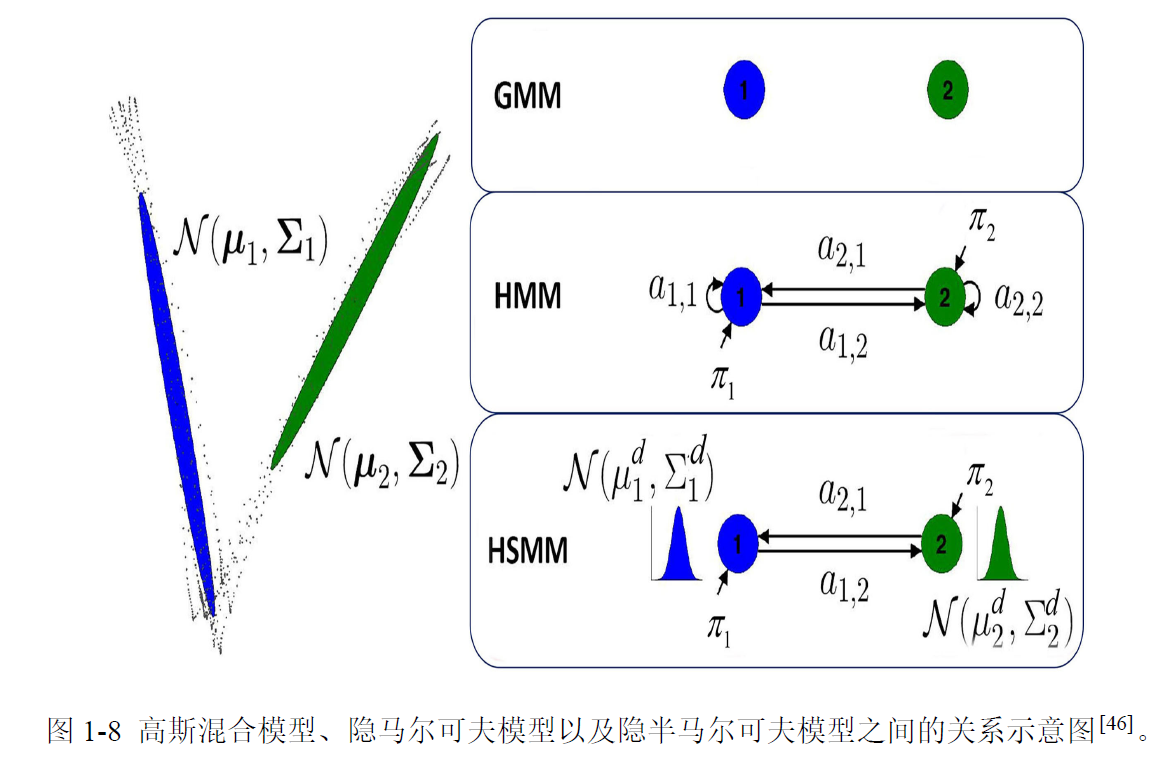
(半)隐马尔可夫模型与高斯混合模型在技能表达上具有一定相似性,区别在于模型中各状态之间是否有联系。高斯混合模型、隐马尔可夫模型以及半隐马尔可夫模型之间的关系示意图如图1-8所示。以两个状态为例,在高斯混合模型中两个状态相互独立,两个状态之间没有任何关联信息;在隐马尔可夫模型中,一个状态可以向另外一个状态以一定的概率发生状态转移;在半隐马尔可夫模型中,不但可以状态转移,每个状态还以高斯分布的形式有持续时间,因而可以在技能表达中包含更丰富的时间信息。
文献[49] 提出了一个基于GMM 模型的机器人技模仿学习框架,用GMM 模型学习的结果初始化后续的优化模型,这一点与前文所述的基于DMP 模型的强化学习方法比较类似。可以利用高斯混合模型学习示教数据中不同变量之间关联信息[50] 来提高技能学习效果,或者通过间接学习一种稳定非线性系统(Stable estimator of dynamical systems, SEDS) 来学习示教信息[51]。文献[48] 提出利用高斯混合模型来学习同时带有关节空间与任务空间限制的任务,并将所学技能泛化到新的任务情况。

有学者在原始GMM 基础上发展出了几种变种模型。例如,文献[53] 提出了一种增量式局部在线高斯(混合)回归模型(Incremental, Local and Online variation of GaussianMixture Regression,ILO-GMR),可以使机器人在线学习新技能,从而避免重复调整模型参数,提高了技能学习效率。
文献[54] 提出了参数化高斯混合模型(Task-ParameterizedGaussian Mixture Model, TP-GMM),把任务信息参数集成到模型学习过程中,因而在任务复现阶段能够对外部环境有一定的感知作用。文献[55] 进一步对TP-GMM 模型进行了优化,降低了模型对外部环境信息的依赖度。文献[56] 也对该模型进行了优化,把模型参数学习问题转为一个低维度的优化问题,从而降低了模型学习的成本。文献[52] 将高斯混合模型从笛卡尔空间拓展到了黎曼流形域,可以更好地表达机械臂末端在任务空间的旋转信息,并将该模型应用到了机器人倒水作业中,如图1-9所示。目前,高斯混合模型已经被应用于机器人辅助手术[57]、软体机器人的技能学习[58,59]、装配[60] 等实验场景中。
文献[62] 利用隐马尔可夫模型进行类人机器人的技能示教学习,实验表明该模型可以相对更好地表达不同状态之间的关联性。文献[61] 提出了HMM-GMR 技能表达框架,其中,利用HMM 对示教数据建模,而用GMR 模型生成最终的运动策略控制命令,并将该模型应用到了击打乒乓球和喂食任务(Food-feeding task) 中,如图1-10所示。
文献[63] 集成隐马尔可夫模型与线性参数变化系统(Linear Parameter Varying, LPV),利用LPV 提高HMM 模型中的状态的稳定性,该方法在学习序列化的运动技能方面具有优势。此外,隐马尔可夫模型还被应用到了移动机器人示教学习[64]、金属件加工生产线[65]、机器人刷漆[66]、机器人辅助血管内导管插入手术[67] 等任务场景中。
文献[68] 利用半隐马尔可夫模型学习机器人的示教技能,同时表达运动技能的时间信息与空间信息。相比于HMM 模型,HSMM 模型在运动的时间空间上具有更好的抗干扰能力。文献[69] 利用HSMM 模型把人的运动与机器人的运动在空间与时间两个维度上都关联起来,使得机器人能够对人的状态作出更准确的意图识别,从而也就把对外部的感知信息与机器人的运动控制命令更好地关联起来,该文将HSMM 模型应用到了机器人辅助穿衣任务中,如图1-11所示。文献[70] 改进了原始的HSMM 模型,使得该模型中的每个状态的持续时间不再固定,而是可以自适应地调节,因而在时间信息的表达上能够获得更好的效果。
参考论文:[1]曾超.人-机器人技能传递技术研究[D].华南理工大学,2019.DOI:10.27151/d.cnki.ghnlu.2019.004286.
参考文献
26\] Ijspeert A.J., Nakanishi J., Schaal S.. Trajectory formation for imitation with nonlinear dynamical systems \[C\]. Proceedings 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Expanding the Societal Role of Robotics in the the Next Millennium (Cat. No. 01CH37180), 2001. 2:752--757 \[27\] Ijspeert A. J., Nakanishi J., Schaal S. Movement imitation with nonlinear dynamical systems in humanoid robots\[C\]. Proceedings of the IEEE International Conference on Robotics and Automation. Washington, DC, USA: IEEE, 2002: 1398-1403. \[28\] Ude A., Gams A., Asfour T., et al. Task-specific generalization of discrete and periodic dynamic movement primitives\[J\]. IEEE Transactions on Robotics, 2010, 26(5): 800-815. \[29\] Muelling K., Kober J., Peters J. Learning table tennis with a mixture of motor primitives\[C\]. 2010 10th IEEE-RAS International Conference on Humanoid Robots. Nashville, TN, USA: IEEE, 2010: 411-416. \[30\] Hoffmann H., Pastor P., Park D. H., et al. Biologically-inspired dynamical systems for movement generation: automatic real-time goal adaptation and obstacle avoidance\[C\]. 2009 IEEE International Conference on Robotics and Automation. Kobe, Japan: IEEE, 2009: 2587-2592. \[31\] Rückert E., d'Avella A. Learned parametrized dynamic movement primitives with shared synergies for controlling robotic and musculoskeletal systems\[J\]. Frontiers in Computational Neuroscience, 2013, 7: 138. \[32\] Krug R., Dimitrov D. Model predictive motion control based on generalized dynamical movement primitives\[J\]. Journal of Intelligent \& Robotic Systems, 2015, 77(1): 17-35. \[33\] Meier F., Schaal S. A probabilistic representation for dynamic movement primitives\[J\]. arXiv preprint arXiv:1612.05932, 2016. \[34\] Gams A., Nemec B., Ijspeert A. J., et al. Coupling movement primitives: Interaction with the environment and bimanual tasks\[J\]. IEEE Transactions on Robotics, 2014, 30(4): 816-830. \[35\] Gašpar T., Nemec B., Morimoto J., et al. Skill learning and action recognition by arc-length dynamic movement primitives\[J\]. Robotics and Autonomous Systems, 2018, 100: 225-235. \[36\] Kober J., Mohler B., Peters J. Learning perceptual coupling for motor primitives\[C\]. 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice, France: IEEE, 2008: 834-839. \[37\] Stulp F., Theodorou E. A., Schaal S. Reinforcement learning with sequences of motion primitives for robust manipulation\[J\]. IEEE Transactions on Robotics, 2012, 28(6): 1360-1370. \[38\] Yin X., Chen Q. Learning nonlinear dynamical system for movement primitives\[C\]. 2014 IEEE International Conference on Systems, Man, and Cybernetics. San Diego, CA, USA: IEEE, 2014: 3761-3766. \[39\] Matsubara T., Hyon S. H., Morimoto J. Learning stylistic dynamic movement primitives from multiple demonstrations\[C\]. 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, China: IEEE, 2010: 1277-1283. \[40\] Kober J., Peters J. R. Policy search for motor primitives in robotics\[C\]. Advances in Neural Information Processing Systems 22 (NIPS 2009). Vancouver, British Columbia, Canada: Curran Associates, Inc., 2009: 849-856. \[41\] Theodorou E., Buchli J., Schaal S. A generalized path integral control approach to reinforcement learning\[J\]. Journal of Machine Learning Research, 2010, 11(Nov): 3137-3181. \[42\] Buchli J., Stulp F., Theodorou E., et al. Learning variable impedance control\[J\]. The International Journal of Robotics Research, 2011, 30(7): 820-833. \[43\] Li Z., Zhao T., Chen F., et al. Reinforcement learning of manipulation and grasping using dynamical movement primitives for a humanoidlike mobile manipulator\[J\]. IEEE/ASME Transactions on Mechatronics, 2017, 23(1): 121-131. \[44\] Stulp F., Sigaud O. Robot skill learning: From reinforcement learning to evolution strategies\[J\]. Paladyn, Journal of Behavioral Robotics, 2013, 4(1): 49-61. \[45\] Hu Y., Wu X., Geng P., et al. Evolution strategies learning with variable impedance control for grasping under uncertainty\[J\]. IEEE Transactions on Industrial Electronics, 2018, 66(10): 7788-7799. \[46\] Calinon S., Lee D. Learning control\[M\]// Humanoid Robotics: a Reference. Berlin, Germany: Springer, 2016: 1-52. \[47\] Calinon S., Bruno D. A programming by demonstration model combining statistics, dynamical systems and optimal control\[R\]. Martigny, Switzerland: Idiap Research Institute, 2014. \[48\] Calinon S., Guenter F., Billard A. On learning, representing, and generalizing a task in a humanoid robot\[J\]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007, 37(2): 286-298. \[49\] Muhlig M., Gienger M., Hellbach S., et al. Task-level imitation learning using variance-based movement optimization\[C\]. 2009 IEEE International Conference on Robotics and Automation. Kobe, Japan: IEEE, 2009: 1177-1184. \[50\] Gribovskaya E., Khansari-Zadeh S. M., Billard A. Learning non-linear multivariate dynamics of motion in robotic manipulators\[J\]. The International Journal of Robotics Research, 2011, 30(1): 80-117. \[51\] Khansari-Zadeh S. M., Billard A. Learning stable nonlinear dynamical systems with Gaussian mixture models\[J\]. IEEE Transactions on Robotics, 2011, 27(5): 943-957. \[52\] Zeestraten M. J., Havoutis I., Silvério J., et al. An approach for imitation learning on Riemannian manifolds\[J\]. IEEE Robotics and Automation Letters, 2017, 2(3): 1240-1247.