Adaptive OFDM Radar for Target Detection in Multipath Scenarios

摘要------我们开发了用于在存在多径反射的情况下（例如在城市环境中）检测移动目标的方法。我们利用多径传播来增加雷达系统的空间分集，并在不同路径上提供不同的多普勒频移。我们采用宽带正交频分复用（OFDM）信号以增加系统的频率分集，因为目标的不同散射中心在不同频率下会产生不同的谐振。

为了克服传统 OFDM 的峰均功率比（PAPR）问题，我们还使用了恒包络 OFDM（constant-envelope OFDM，CE-OFDM）信令方案。

首先，我们考虑一个简单的场景，即雷达仅接收有限数量的镜面反射多径信号（specularly reflected multipath signals）。在广义多元方差分析（generalized multi-variate analysis of variance，GMANOVA）框架下，我们针对 OFDM 和 CE-OFDM 信令方法开发了参数测量模型，并采用广义似然比（generalized likelihood ratio，GLR）检验来判定特定距离单元中是否存在目标。
接着，我们提出了一种算法，用于优化设计下一个相干处理间隔的 OFDM 发射波形参数。
此外，我们扩展了模型以研究测量噪声中的时间相关性方面。
我们提供了几个数值示例来说明所提出的检测器的性能特征，并展示了由于自适应 OFDM 波形设计而实现的性能提升。

索引词------自适应波形设计，渐近性能分析，多径，OFDM 雷达，目标检测，城市场景。

文章目录

- [II. PROBLEM DESCRIPTION AND MODELING](#II. PROBLEM DESCRIPTION AND MODELING)
- - [A. OFDM Measurement Model](#A. OFDM Measurement Model)

然后，在第 IV 节中，我们提出一个准则来自适应地计算下一个发射波形的参数。为了构建这样一个准则，我们首先研究在假设目标速度已知的情况下，OFDM 和 CE-OFDM 模型的 GLR 检验统计量的性能特征。然而，这种分析并不能表征我们的检测器的检测性能，因为在这些检测器中目标速度是未知的。对已知目标速度的分析表明，对于 OFDM（具有大量时间样本）和 CE-OFDM（具有有限数量时间样本）模型，GLR 检验结果都会产生恒虚警率（CFAR）检测器，并且检测性能通过备择假设下分布的相应非中心参数依赖于系统参数。这意味着可以通过最大化这些非中心参数来提高检测性能。我们将这一思想应用于我们的问题，并建立优化问题，以在固定的传输能量约束下，选择使该非中心参数表达式最大化的下一个发射波形参数。对于 OFDM 模型，我们要证明该优化问题的解是一个特征向量，它对应于一个取决于目标、杂波和噪声参数的矩阵的最大特征值。然而，对于 CE-OFDM 模型，我们无法以这种方式提高检测性能，因为非中心参数不依赖于发射波形。

稍后在本文的第 V 节中，我们放宽时间白噪声的假设，以研究时间相关的测量噪声过程对我们模型的影响。在某些雷达应用中，特别是在高脉冲重复频率（PRF）[31], [32] 下，存在时间相关性。为了对时间相关矩阵进行建模，我们研究了统计学中称为最近邻分析 [33], [34] 的一个分支，并给出了随后的检测检验。

II. PROBLEM DESCRIPTION AND MODELING

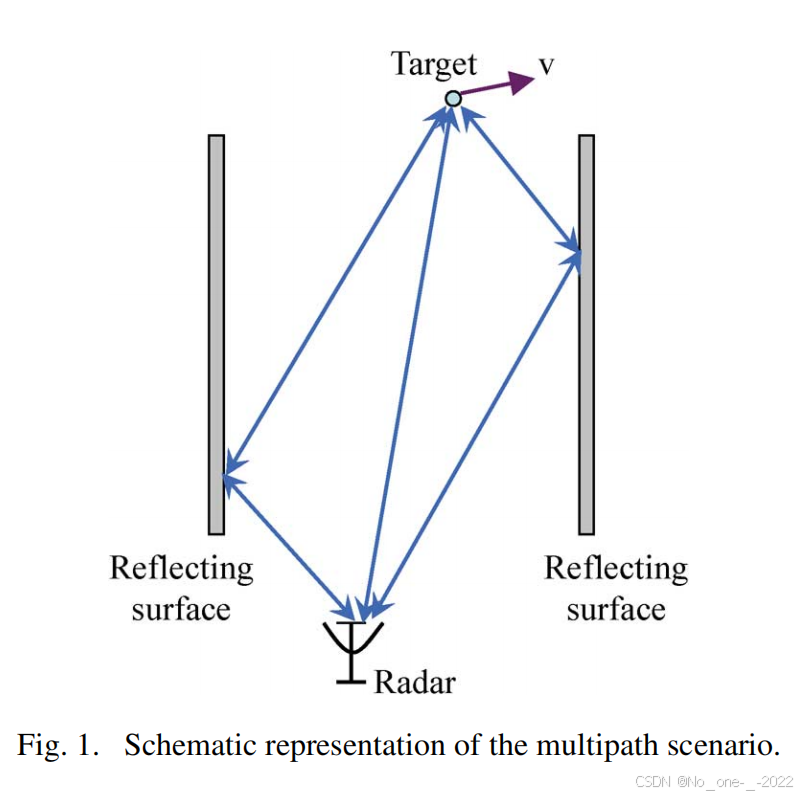
我们考虑在多径丰富的环境中，相对于雷达以恒定相对速度 v ⃗ \vec{\boldsymbol{v}} v 移动的远场点目标，如图 1 所示。在工作频率下，我们假设反射面仅产生雷达信号的镜面反射。我们假设雷达完全了解受监视的环境。

因此，对于每个距离单元（range cell），雷达知道雷达与目标之间可能的多径数量 ( P P P) 以及沿每条路径的波达方向 (DOA) 单位向量 ( u p , p = 0 , 1 , ... , P − 1 \boldsymbol{u}_p, p=0, 1, \dots, P-1 up,p=0,1,...,P−1)。
在这种情况下，我们首先介绍 OFDM 和 CE-OFDM 信令技术的参数测量模型。然后，我们讨论关于杂波和噪声的统计假设。

A. OFDM Measurement Model

我们考虑一个具有 L L L 个有效子载波、带宽为 B B B Hz 且脉冲持续时间为 T T T 秒的 OFDM 信令系统 [15]。令 a = [ a 0 , a 1 , ... , a L − 1 ] T \boldsymbol{a} = [a_0, a_1, \dots, a_{L-1}]^T a=[a0,a1,...,aL−1]T 表示在 L L L 个子载波上传输的复加权，满足 ∑ l = 0 L − 1 ∣ a l ∣ 2 = 1 \sum_{l=0}^{L-1} |a_l|^2 = 1 ∑l=0L−1∣al∣2=1。那么，发射信号的复包络可以表示为

s OFDM ( t ) = ∑ l = 0 L − 1 a l e j 2 π l Δ f t (1) s_{\text{OFDM}}(t) = \sum_{l=0}^{L-1} a_l e^{j2\pi l \Delta f t} \tag{1} sOFDM(t)=l=0∑L−1alej2πlΔft(1)

其中 Δ f = B / ( L + 1 ) = 1 / T \Delta f = B/(L+1) = 1/T Δf=B/(L+1)=1/T 表示子载波间隔。令 f c f_c fc 为工作载波频率，则发射信号由下式给出

s ~ ( t ) = 2 Re { ∑ l = 0 L − 1 a l e j 2 π f l t } (2) \tilde{s}(t) = 2\text{Re}\left\{ \sum_{l=0}^{L-1} a_l e^{j2\pi f_l t} \right\} \tag{2} s~(t)=2Re{l=0∑L−1alej2πflt}(2)

其中 f l = f c + l Δ f f_l = f_c + l\Delta f fl=fc+lΔf 表示第 l l l 个子载波频率。交换实部和求和算子，我们也可以将 (2) 重写为

s ~ ( t ) = ∑ l = 0 L − 1 s ~ l ( t ) (3) \tilde{s}(t) = \sum_{l=0}^{L-1} \tilde{s}_l(t) \tag{3} s~(t)=l=0∑L−1s~l(t)(3)

其中

s ~ l ( t ) = 2 Re { a l e j 2 π f l t } (4) \tilde{s}_l(t) = 2\text{Re}\left\{ a_l e^{j2\pi f_l t} \right\} \tag{4} s~l(t)=2Re{alej2πflt}(4)

表示仅由第 l l l 个子载波引起的发射信号。那么，仅由第 l l l 个子载波引起的沿第 p p p 条路径（由 DOA 向量 u p \boldsymbol{u}_p up 表示）的接收信号可以写为

y ~ l p ( t ) = x l p s ~ l ( γ p ( t − τ p ) ) + e ~ l p ( t ) (5) \tilde{y}{lp}(t) = x{lp} \tilde{s}l (\gamma_p (t - \tau_p)) + \tilde{e}{lp}(t) \tag{5} y~lp(t)=xlps~l(γp(t−τp))+e~lp(t)(5)

其中 x l p x_{lp} xlp 是一个复量，表示目标沿第 l l l 个子信道和第 p p p 条路径的散射系数； γ p = 1 + β p \gamma_p = 1 + \beta_p γp=1+βp，其中 β p = 2 ⟨ v ⃗ , u p ⟩ / c \beta_p = 2\langle \vec{\boldsymbol{v}}, \boldsymbol{u}p \rangle / c βp=2⟨v ,up⟩/c 是沿第 p p p 条路径的相对多普勒频移， c c c 是传播速度； τ p \tau_p τp 是雷达与目标之间沿第 p p p 条路径的往返延迟； e ~ l p \tilde{e}{lp} e~lp 表示沿第 l l l 个子信道和第 p p p 条路径的杂波和测量噪声。因此（Therefore）， L L L-载波 OFDM 信号在所有 P P P 条可用路径上的接收信号由下式给出

y ~ ( t ) = ∑ l = 0 L − 1 ∑ p = 0 P − 1 y ~ l p ( t ) = 2 Re { ∑ l = 0 L − 1 ∑ p = 0 P − 1 a l x l p e j 2 π f l γ p ( t − τ p ) } + e ~ ( t ) , = 2 Re { ∑ l = 0 L − 1 ∑ p = 0 P − 1 a l x l p e j 2 π ( f c + l Δ f ) ( 1 + β p ) ( t − τ p ) } + e ~ ( t ) = 2 Re { ∑ l = 0 L − 1 ∑ p = 0 P − 1 a l x l p e j 2 π l Δ f ( 1 + β p ) ( t − τ p ) × e − j 2 π f c ( 1 + β p ) τ p e j 2 π f c β p t e j 2 π f c t } + e ~ ( t ) (6) \begin{aligned} \tilde{y}(t) &= \sum_{l=0}^{L-1} \sum_{p=0}^{P-1} \tilde{y}{lp}(t) \\ &= 2\text{Re}\left\{ \sum{l=0}^{L-1} \sum_{p=0}^{P-1} a_l x_{lp} e^{j2\pi f_l \gamma_p (t-\tau_p)} \right\} + \tilde{e}(t), \\ &= 2\text{Re}\left\{ \sum_{l=0}^{L-1} \sum_{p=0}^{P-1} a_l x_{lp} e^{j2\pi (f_c+l\Delta f)(1+\beta_p)(t-\tau_p)} \right\} + \tilde{e}(t) \\ &= 2\text{Re}\left\{ \sum_{l=0}^{L-1} \sum_{p=0}^{P-1} a_l x_{lp} e^{j2\pi l \Delta f(1+\beta_p)(t-\tau_p)} \right. \\ &\quad \times \left. e^{-j2\pi f_c(1+\beta_p)\tau_p} e^{j2\pi f_c \beta_p t} e^{j2\pi f_c t} \right\} + \tilde{e}(t) \end{aligned}\tag{6} y~(t)=l=0∑L−1p=0∑P−1y~lp(t)=2Re{l=0∑L−1p=0∑P−1alxlpej2πflγp(t−τp)}+e~(t),=2Re{l=0∑L−1p=0∑P−1alxlpej2π(fc+lΔf)(1+βp)(t−τp)}+e~(t)=2Re{l=0∑L−1p=0∑P−1alxlpej2πlΔf(1+βp)(t−τp)×e−j2πfc(1+βp)τpej2πfcβptej2πfct}+e~(t)(6)

因此，相应的复包络由下式给出

y OFDM ( t ) = ∑ l = 0 L − 1 ∑ p = 0 P − 1 a l x l p e j 2 π l Δ f ( 1 + β p ) ( t − τ p ) × e − j 2 π f c ( 1 + β p ) τ p e j 2 π f c β p t + e ( t ) . (7) y_{\text{OFDM}}(t) = \sum_{l=0}^{L-1} \sum_{p=0}^{P-1} a_l x_{lp} e^{j2\pi l \Delta f(1+\beta_p)(t-\tau_p)} \times e^{-j2\pi f_c(1+\beta_p)\tau_p} e^{j2\pi f_c \beta_p t} + e(t). \tag{7} yOFDM(t)=l=0∑L−1p=0∑P−1alxlpej2πlΔf(1+βp)(t−τp)×e−j2πfc(1+βp)τpej2πfcβpt+e(t).(7)

此时我们假设任意两个多径信号之间的相对时间间隙相比于实际往返延迟非常小，即对于 p = 0 , ... , P − 1 p = 0, \dots, P-1 p=0,...,P−1，有 τ p ≈ τ 0 \tau_p \approx \tau_0 τp≈τ0。这些假设在多径到达的路径长度差异很小的系统中是合理的（例如，距离远大于宽度的狭窄城市峡谷）。
此外，我们将 τ 0 \tau_0 τ0 表示为对应于所考虑的距离单元的往返延迟。那么，通过选择 t = τ 0 + n T PRI , n = 0 , 1 , ... , N − 1 t = \tau_0 + nT_{\text{PRI}}, n = 0, 1, \dots, N-1 t=τ0+nTPRI,n=0,1,...,N−1，往返延迟的信息可以自动包含在模型中，其中 T PRI T_{\text{PRI}} TPRI 是脉冲重复间隔（PRI），而 N N N 是给定相干处理间隔（CPI）内的时间测量次数。

因此，对应于包含目标的特定距离单元，第 l l l 个子信道输出端的接收信号复包络为

y l OFDM ( n ) = ∑ p = 0 P − 1 a l x l p ϕ l p ( n ) + e l ( n ) , for l = 0 , 1 , ... , L − 1 , n = 0 , 1 , ... , N − 1 (8) y_{l_{\text{OFDM}}}(n) = \sum_{p=0}^{P-1} a_l x_{lp} \phi_{lp}(n) + e_l(n), \quad \text{for } l = 0, 1, \dots, L-1, n = 0, 1, \dots, N-1 \tag{8} ylOFDM(n)=p=0∑P−1alxlpϕlp(n)+el(n),for l=0,1,...,L−1,n=0,1,...,N−1(8)

其中

ϕ l p ( n ) ≜ e − j 2 π f l τ 0 e j 2 π f l β p n T PRI . (9) \phi_{lp}(n) \triangleq e^{-j2\pi f_l \tau_0} e^{j2\pi f_l \beta_p n T_{\text{PRI}}} . \tag{9} ϕlp(n)≜e−j2πflτ0ej2πflβpnTPRI.(9)

从公式 (7) 推导至公式 (9) 主要经过相位项整理 、代入采样时间 与OFDM 解调三个步骤。

整理相位项
首先利用 f l = f c + l Δ f f_l = f_c + l\Delta f fl=fc+lΔf，将公式 (7) 中的指数项按"多普勒项（含 β p \beta_p βp）"和"静态项"分组：

Total Phase = e j 2 π l Δ f ( t − τ p ) e − j 2 π f c τ p ⏟ 静态项 × e j 2 π f l β p ( t − τ p ) ⏟ 多普勒项 \text{Total Phase} = \underbrace{e^{j2\pi l \Delta f (t-\tau_p)} e^{-j2\pi f_c \tau_p}}{\text{静态项}} \times \underbrace{e^{j2\pi f_l \beta_p (t-\tau_p)}}{\text{多普勒项}} Total Phase=静态项 ej2πlΔf(t−τp)e−j2πfcτp×多普勒项 ej2πflβp(t−τp)

代入采样时间与近似

代入采样时刻 t = τ 0 + n T PRI t = \tau_0 + nT_{\text{PRI}} t=τ0+nTPRI 并应用近似条件 τ p ≈ τ 0 \tau_p \approx \tau_0 τp≈τ0，则有 t − τ p ≈ n T PRI t - \tau_p \approx nT_{\text{PRI}} t−τp≈nTPRI。

多普勒项化简：

直接代入后得到公式 (9) 的后半部分：
e j 2 π f l β p n T PRI e^{j2\pi f_l \beta_p n T_{\text{PRI}}} ej2πflβpnTPRI

静态项化简：

代入后变为：
e j 2 π l Δ f n T PRI ⋅ e − j 2 π f c τ 0 e^{j2\pi l \Delta f nT_{\text{PRI}}} \cdot e^{-j2\pi f_c \tau_0} ej2πlΔfnTPRI⋅e−j2πfcτ0
(注：此处暂未包含 e − j 2 π l Δ f τ 0 e^{-j2\pi l \Delta f \tau_0} e−j2πlΔfτ0，需结合解调步骤)

OFDM 解调（关键步骤）

文中"第 l l l 个子信道的输出"意味着在接收端需去除发射信号的参考相位 e j 2 π l Δ f t e^{j2\pi l \Delta f t} ej2πlΔft。

发射机参考相位 （在 t = τ 0 + n T PRI t = \tau_0 + nT_{\text{PRI}} t=τ0+nTPRI 时）：
e j 2 π l Δ f ( τ 0 + n T PRI ) = e j 2 π l Δ f τ 0 ⋅ e j 2 π l Δ f n T PRI e^{j2\pi l \Delta f (\tau_0 + nT_{\text{PRI}})} = e^{j2\pi l \Delta f \tau_0} \cdot e^{j2\pi l \Delta f nT_{\text{PRI}}} ej2πlΔf(τ0+nTPRI)=ej2πlΔfτ0⋅ej2πlΔfnTPRI

解调后的静态相位 （接收相位除以参考相位）：
e j 2 π l Δ f n T PRI ⋅ e − j 2 π f c τ 0 e j 2 π l Δ f τ 0 ⋅ e j 2 π l Δ f n T PRI = e − j 2 π f c τ 0 ⋅ e − j 2 π l Δ f τ 0 = e − j 2 π f l τ 0 \frac{e^{j2\pi l \Delta f nT_{\text{PRI}}} \cdot e^{-j2\pi f_c \tau_0}}{e^{j2\pi l \Delta f \tau_0} \cdot e^{j2\pi l \Delta f nT_{\text{PRI}}}} = e^{-j2\pi f_c \tau_0} \cdot e^{-j2\pi l \Delta f \tau_0} = e^{-j2\pi f_l \tau_0} ej2πlΔfτ0⋅ej2πlΔfnTPRIej2πlΔfnTPRI⋅e−j2πfcτ0=e−j2πfcτ0⋅e−j2πlΔfτ0=e−j2πflτ0

结论

将解调后的静态相位 与多普勒相位 合并，即得到公式 (9)：
ϕ l p ( n ) ≜ e − j 2 π f l τ 0 ⏟ 解调后延迟项 e j 2 π f l β p n T PRI ⏟ 多普勒项 \phi_{lp}(n) \triangleq \underbrace{e^{-j2\pi f_l \tau_0}}{\text{解调后延迟项}} \underbrace{e^{j2\pi f_l \beta_p n T{\text{PRI}}}}_{\text{多普勒项}} ϕlp(n)≜解调后延迟项 e−j2πflτ0多普勒项 ej2πflβpnTPRI

将所有 L L L 个子信道的测量值堆叠成一个维度为 L × 1 L \times 1 L×1 的列向量，我们得到

y OFDM ( n ) = A ( a ) X ϕ ( n , v ) + e ( n ) , for n = 0 , ... , N − 1 (10) \boldsymbol{y}_{\text{OFDM}}(n) = \boldsymbol{A}(\boldsymbol{a})\boldsymbol{X}\boldsymbol{\phi}(n, \boldsymbol{v}) + \boldsymbol{e}(n), \quad \text{for } n = 0, \dots, N-1 \tag{10} yOFDM(n)=A(a)Xϕ(n,v)+e(n),for n=0,...,N−1(10)

其中

y OFDM ( n ) = [ y 0 OFDM ( n ) , y 1 OFDM ( n ) , ... , y L − 1 OFDM ( n ) ] T \boldsymbol{y}{\text{OFDM}}(n) = [y{0_{\text{OFDM}}}(n), y_{1_{\text{OFDM}}}(n), \dots, y_{L-1_{\text{OFDM}}}(n)]^T yOFDM(n)=[y0OFDM(n),y1OFDM(n),...,yL−1OFDM(n)]T；
A = diag ( a ) \boldsymbol{A} = \text{diag}(\boldsymbol{a}) A=diag(a) 是包含传输加权 a \boldsymbol{a} a 的 L × L L \times L L×L 复对角矩阵；
X = blkdiag ( x 0 T , x 1 T , ... , x L − 1 T ) \boldsymbol{X} = \text{blkdiag}(\boldsymbol{x}0^T, \boldsymbol{x}1^T, \dots, \boldsymbol{x}{L-1}^T) X=blkdiag(x0T,x1T,...,xL−1T) 是一个 L × L P L \times LP L×LP 复矩形块对角矩阵，其中每个非零块 x l = [ x l 0 , x l 1 , ... , x l P − 1 ] T , l = 0 , 1 , ... , L − 1 \boldsymbol{x}l = [x{l0}, x{l1}, \dots, x_{lP-1}]^T, l = 0, 1, \dots, L-1 xl=[xl0,xl1,...,xlP−1]T,l=0,1,...,L−1，表示目标在第 l l l 个子信道上所有 P P P 条多径的散射系数；
ϕ ( n , v ) = [ ϕ 0 ( n , v ) T ϕ 1 ( n , v ) T ⋯ ϕ L − 1 ( n , v ) T ] T \boldsymbol{\phi}(n, \boldsymbol{v}) = [\boldsymbol{\phi}0(n, \boldsymbol{v})^T \boldsymbol{\phi}1(n, \boldsymbol{v})^T \cdots \boldsymbol{\phi}{L-1}(n, \boldsymbol{v})^T]^T ϕ(n,v)=[ϕ0(n,v)Tϕ1(n,v)T⋯ϕL−1(n,v)T]T 是一个 L P × 1 LP \times 1 LP×1 复向量，其中 ϕ l ( n , v ) = [ ϕ l 0 ( n ) , ϕ l 1 ( n ) , ... , ϕ l P − 1 ( n ) ] T , l = 0 , 1 , ... , L − 1 \boldsymbol{\phi}l(n, \boldsymbol{v}) = [\phi{l0}(n), \phi{l1}(n), \dots, \phi_{lP-1}(n)]^T, l = 0, 1, \dots, L-1 ϕl(n,v)=[ϕl0(n),ϕl1(n),...,ϕlP−1(n)]T,l=0,1,...,L−1，包含目标在第 l l l 个子信道上所有 P P P 条多径的多普勒信息；
v \boldsymbol{v} v 是包含未知目标速度分量的列向量；
e ( n ) = [ e 0 ( n ) , e 1 ( n ) , ... , e L − 1 ( n ) ] T \boldsymbol{e}(n) = [e_0(n), e_1(n), \dots, e_{L-1}(n)]^T e(n)=[e0(n),e1(n),...,eL−1(n)]T 是杂波回波、测量噪声和同信道干扰的 L × 1 L \times 1 L×1 向量。

实际上， f D ⋅ n ⋅ T PRI f_D \cdot n \cdot T_{\text{PRI}} fD⋅n⋅TPRI 与原文中的 f l β p ⋅ n ⋅ T PRI f_l \beta_p \cdot n \cdot T_{\text{PRI}} flβp⋅n⋅TPRI 在物理意义上是完全等价的。原文之所以使用 f l β p f_l \beta_p flβp，是为了强调宽带雷达中多普勒频率随子载波频率变化的特性。

数学上的等价性

根据原文定义， β p \beta_p βp 是相对速度引起的时间膨胀因子：
β p = 2 ⟨ v ⃗ , u p ⟩ c = 2 v r c (A) \beta_p = \frac{2\langle \vec{\boldsymbol{v}}, \boldsymbol{u}_p \rangle}{c} = \frac{2 v_r}{c} \tag{A} βp=c2⟨v ,up⟩=c2vr(A)

其中 v r v_r vr 是径向相对速度。而标准的多普勒频率 f D f_D fD 定义为：
f D = 2 v r λ = f ⋅ 2 v r c (B) f_D = \frac{2 v_r}{\lambda} = f \cdot \frac{2 v_r}{c} \tag{B} fD=λ2vr=f⋅c2vr(B)

将 (A) 代入 (B)，可得：
f D = f ⋅ ( 2 v r c ) ⏟ β p = f ⋅ β p f_D = f \cdot \underbrace{\left( \frac{2 v_r}{c} \right)}_{\beta_p} = f \cdot \beta_p fD=f⋅βp (c2vr)=f⋅βp

因此，公式中的 f l β p f_l \beta_p flβp 正是第 l l l 个子载波上的多普勒频率 f D , l f_{D,l} fD,l。

为什么要写成 f l β p f_l \beta_p flβp？

这体现了宽带 OFDM 雷达的专业细节处理：

宽带效应（Frequency Dependent Doppler） ：
OFDM 系统中不同子载波频率 f l f_l fl 差异较大。由 f D , l = f l ⋅ β p f_{D,l} = f_l \cdot \beta_p fD,l=fl⋅βp 可知，高频子载波的多普勒频移大于低频子载波。若直接写成单一 f D f_D fD，通常暗示窄带假设（即忽略频率差异）。

变量统一 ：
前文已定义 γ p = 1 + β p \gamma_p = 1 + \beta_p γp=1+βp。沿用无量纲参数 β p \beta_p βp 可保持公式符号的一致性，无需引入新变量。

总结：

指数项 e j 2 π ( f l β p ) n T PRI e^{j2\pi (f_l \beta_p) n T_{\text{PRI}}} ej2π(flβp)nTPRI 本质上即为 e j 2 π f D , l n T PRI e^{j2\pi f_{D,l} n T_{\text{PRI}}} ej2πfD,lnTPRI，作者的写法是为了精确表达多普勒频移依附于子载波频率 f l f_l fl 存在的物理事实。

然后，将所有时间数据按列拼接成一个 L × N L \times N L×N 矩阵，我们得到如下 OFDM 测量模型：

Y OFDM = A ( a ) X Φ ( v ) + E (11) \boldsymbol{Y}_{\text{OFDM}} = \boldsymbol{A}(\boldsymbol{a})\boldsymbol{X}\boldsymbol{\Phi}(\boldsymbol{v}) + \boldsymbol{E} \tag{11} YOFDM=A(a)XΦ(v)+E(11)

其中

Y OFDM = [ y OFDM ( 0 ) , y OFDM ( 1 ) , ... , y OFDM ( N − 1 ) ] \boldsymbol{Y}{\text{OFDM}} = [\boldsymbol{y}{\text{OFDM}}(0), \boldsymbol{y}{\text{OFDM}}(1), \dots, \boldsymbol{y}{\text{OFDM}}(N-1)] YOFDM=[yOFDM(0),yOFDM(1),...,yOFDM(N−1)]；
Φ ( v ) = [ ϕ ( 0 , v ) , ϕ ( 1 , v ) , ... , ϕ ( N − 1 , v ) ] \boldsymbol{\Phi}(\boldsymbol{v}) = [\boldsymbol{\phi}(0, \boldsymbol{v}), \boldsymbol{\phi}(1, \boldsymbol{v}), \dots, \boldsymbol{\phi}(N-1, \boldsymbol{v})] Φ(v)=[ϕ(0,v),ϕ(1,v),...,ϕ(N−1,v)] 是一个 L P × N LP \times N LP×N 矩阵，包含通过参数 v \boldsymbol{v} v 确定的目标多普勒信息；
E = [ e ( 0 ) , e ( 1 ) , ... , e ( N − 1 ) ] \boldsymbol{E} = [\boldsymbol{e}(0), \boldsymbol{e}(1), \dots, \boldsymbol{e}(N-1)] E=[e(0),e(1),...,e(N−1)] 是一个 L × N L \times N L×N 矩阵，包含杂波回波、噪声和干扰。