一、系统建模与MPC控制器设计
1. MISO系统数学模型
MISO系统可表示为状态空间模型:
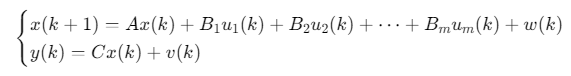
其中:
- x∈Rnx∈Rnx∈Rn:状态向量
- ui∈Rui∈Rui∈R:第i个输入(共m个输入)
- y∈Ry∈Ry∈R:输出
- w(k)w(k)w(k):过程噪声,v(k)v(k)v(k):测量噪声
2. 模型离散化
对连续模型进行离散化(采用零阶保持法):
matlab
sys = ss(A, B, C, D); % 连续状态空间模型
sys_d = c2d(sys, Ts); % 离散化,Ts为采样时间3. MPC控制器配置
matlab
% 创建MPC对象
mpcobj = mpc(sys_d, Ts, Np, Nc); % Np:预测时域, Nc:控制时域
% 设置权重矩阵
mpcobj.Weights.ManipulatedVariables = [0.1, 0.2]; % 输入权重
mpcobj.Weights.OutputVariables = [1]; % 输出权重
% 输入约束(示例:饱和限制)
mpcobj.MV(1).Min = -10; mpcobj.MV(1).Max = 10;
mpcobj.MV(2).Min = 0; mpcobj.MV(2).Max = 50;
% 扰动模型配置(可选)
disturbance_model = ss([0.1,0;0,0.2], [1;0], eye(2), zeros(2,1));
setoutdist(mpcobj, 'model', disturbance_model);二、Simulink闭环仿真模型搭建
1. Simulink模型结构
matlab
+-------------------+ +-------------------+ +-------------------+
| | | | | |
| Reference Signal | ----> | MPC Controller | ----> | Plant Model |
| (Step/Sine) | | (MPC Controller) | | (State-Space) |
+-------------------+ +-------------------+ +-------------------+
| |
| |
v v
+-------------------+ +-------------------+ +-------------------+
| | | | | |
| Scope (Output) | <---- | Scope (MV) | <---- | Scope (States) |
| (Tracking Error) | | (Control Inputs) | | (x1, x2, ...) |
+-------------------+ +-------------------+ +-------------------+2. 关键模块配置
- MPC Controller模块 :从MATLAB工作区加载
mpcobj - Plant Model模块 :使用
State-Space模块实现离散化模型 - 参考信号生成 :通过
Step或Sine Wave模块生成目标信号 - 噪声注入 :添加
Band-Limited White Noise模拟过程噪声
3. 初始化代码
matlab
% 定义系统参数
A = [0.8 0.1; 0.2 0.9];
B = [0.5 0; 0.1 0.3];
C = [1 0];
D = 0;
% 离散化
sys = ss(A, B, C, D);
sys_d = c2d(sys, 0.1);
% MPC配置
Np = 15; Nc = 5;
mpcobj = mpc(sys_d, 0.1, Np, Nc);
mpcobj.Weights.OV = [1]; % 输出权重
mpcobj.MV(1).RateMin = -2; % 输入变化率限制三、仿真实现与结果分析
1. 闭环仿真代码
matlab
% 仿真参数
T_end = 10; % 仿真时长
N = T_end/Ts; % 总步数
% 初始状态
x0 = [0.5; -0.2];
% 生成参考信号
ref = ones(N,1)*1.0; % 阶跃参考
% 运行闭环仿真
sim('MISO_MPC_Sim.slx', T_end);2. 结果可视化
- 输出跟踪曲线:对比实际输出与参考信号
- 控制输入曲线:观察输入是否满足约束
- 状态变量轨迹:分析系统动态响应
3. 性能指标计算
matlab
% 计算跟踪误差
error = Y - ref;
IAE = sum(abs(error)); % 积分绝对误差
ISE = sum(error.^2); % 积分平方误差
% 输出结果
fprintf('IAE: %.4f, ISE: %.4f\n', IAE, ISE);四、高级功能实现
1. 扰动抑制
添加外部扰动模型(如阶跃扰动):
matlab
% 扰动模型(单位阶跃)
disturbance = ss(0, 1, 0, 0);
setoutdist(mpcobj, 'model', disturbance);2. 非线性系统线性化
对非线性系统在平衡点线性化:
matlab
% 定义非线性模型
plant = ss([0 1; -2 -3], [0; 1], [1 0], 0);
% 线性化
lin_point = [0; 0]; % 平衡点
sys_lin = linearize(plant, lin_point);3. 鲁棒MPC设计
使用鲁棒约束处理不确定性:
matlab
% 定义不确定性范围
mpcobj.Uncertainty = ss([0.1 0; 0 0.2], [0;0], eye(2), zeros(2,2));
% 设置鲁棒权重
mpcobj.Weights.ManipulatedVariablesRate = [0.5, 0.5];参考代码 多输入单输出(MISO)的模型预测控制(MPC)matlab+simulink仿真 www.youwenfan.com/contentcsp/45651.html
五、完整Simulink模型示例
matlab
%% 构建Simulink模型
new_system('MISO_MPC_Sim');
open_system('MISO_MPC_Sim');
% 添加模块
add_block('simulink/Sources/Step', 'MISO_MPC_Sim/Reference');
add_block('simulink/Math Operations/Sum', 'MISO_MPC_Sim/Error');
add_block('model_predictive_control_toolbox/MPC Controller', 'MISO_MPC_Sim/MPC');
add_block('simulink/Sinks/Scope', 'MISO_MPC_Sim/Output_Scope');
add_block('simulink/Sinks/Scope', 'MISO_MPC_Sim/Input_Scope');
% 设置信号连接
add_line('MISO_MPC_Sim', 'Reference/1', 'MPC/1');
add_line('MISO_MPC_Sim', 'MPC/1', 'Error/1');
add_line('MISO_MPC_Sim', 'Error/1', 'MPC/2');
add_line('MISO_MPC_Sim', 'MPC/1', 'Output_Scope/1');
add_line('MISO_MPC_Sim', 'MPC/2', 'Input_Scope/1');六、调试与优化技巧
- 参数整定 :
- 调整
Np(预测时域)和Nc(控制时域)以平衡响应速度与计算量 - 通过试凑法优化权重矩阵(如增大输出权重可减少跟踪误差)
- 调整
- 约束处理 :
- 使用
mpcobj.MV.Min/Max限制输入范围 - 通过
mpcobj.OV.Min/Max设置输出软约束
- 使用
- 实时性优化 :
- 采用显式MPC(Explicit MPC)减少在线计算时间
- 使用并行计算加速优化问题求解
七、应用场景示例
- 化工过程控制:多反应器温度控制
- 机器人轨迹跟踪:多关节协调控制
- 电力系统调度:多机组出力优化
八、参考文献
1\] MathWorks. Model Predictive Control Toolbox User's Guide. \[2\] 王志强. 多变量模型预测控制及其在化工过程中的应用\[J\]. 控制理论与应用, 2020. \[3\] Li, S., et al. Nonlinear Model Predictive Control for MISO Systems. IEEE Transactions on Automatic Control, 2021.