我去过很多工厂,大家都知道要设置缓冲区,而缓冲区要设计多大,学问可就大了,本文对此做了深入分析。
本篇内容主要摘译自:Hewlett-Packard Uses Operations Research to
Improve the Design of a Printer Production
Line 在本文翻译过程中去掉了一些与当时商业环境相关的内容,并添加了很少量自己的内容。
1993年,惠普公司在华盛顿州的温哥华市建立了一条喷墨打印机生产线。该系统在投入生产后,由于速度 和可靠性不达标 ,未能满足预期的生产目标。当时喷墨打印机市场的迅猛扩张意味着产能直接关联着利润。麻省理工学院的研究人员运用分析方法确定了影响产能的核心因素,并通过增设小型缓冲区解决了由设备故障引起的产能问题。惠普采纳这些研究成果后,生产效率提升了50%,额外收入达到约2.8亿美元,此外还包括来自相关产品、替换墨盒、介质和相关项目的收入。
这个项目之所以成功,特别归功于其时机选择。技术固然重要,但并非唯一。最关键的是,惠普的管理层愿意去构建、支持并执行基于这项尚未验证的技术的设计方案。在面对巨大压力和迫切需要满足激进的产品推进计划的情况下,他们选择了冒险。他们不得不同时处理硬件、信息系统和人员的变动,以期达到商业利益。那么,惠普的打印机生产线遇到了什么问题,MIT的专家又是如何解决这些问题的呢?
下面是惠普打印机生产线的原有系统示意图:
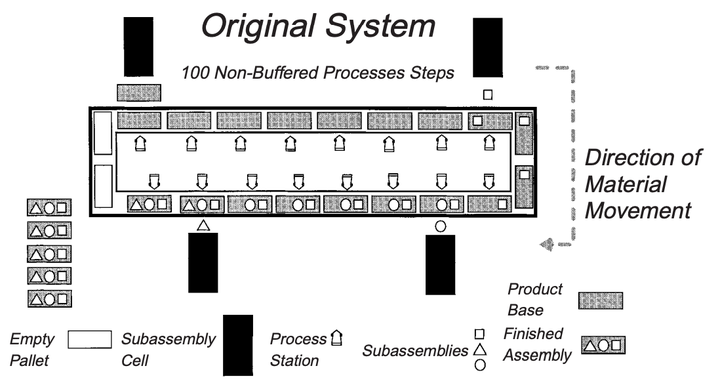
图1:原始系统设计
Empty pallet: 空托盘
Subassembly cell: 子组件单元
Process station: 工序站
Subassemblies: 子组件
Product base: 产品基座
Finished assembly: 完成的装配件
在原始系统设计中,产品基座在左上方的子装配单元(黑色矩形)中组装。它被固定在托盘上,并在主环线上顺时针移动,同时执行各种操作。第一个子装配单元在右上方添加。在进行其他操作并添加更多子装配件后,完成的打印机构从托盘上分离下来。托盘留在系统中,而完成的组件被向下游移动。主环路包含30个自动化工作站。每个子装配单元完成的工作量大约相当于四个主环路工作站。系统设计中基本没有在制品库存空间。
在原始的产线设计中,输送机将托盘从一个工位移到另一个工位。托盘先从接收一个空的产品基座。随后,这个基座会随着托盘顺时针绕着输送机移动,基座在沿途的每个工位加工。每隔几个工位,就会向机构中添加另一个主要组件。这种操作持续进行,直到最终组装成一台完成的打印机并释放托盘,以接收另一个产品基座。在整个生产过程中并没有缓冲区临时存放半成品。
生产效率是工作时间与可用总时间的比率。或者,它是一个时间段内的实际生产量与在没有任何机器故障情况下的生产量之比。由于机器之间的相互作用,生产线的效率低于效率最低的机器的效率。由于维修和故障是随机的,生产量也就是随机的。这里我们只考虑机器故障和由于机器相互作用导致的闲置作为停机时间的一种形式。其他一些中断,如工人缺勤,可以类似处理。其他的,如多产品系统中的设置,则必须采用不同的方法处理。
机器相互作用表现为 "饥饿" 和 "阻塞" 的形式。如果两台机器之间没有缓冲区,并且上游机器发生故障,则下游机器会立即"饥饿",被迫闲置,因为它没有东西可以加工。如果下游机器发生故障,则上游机器会因为被"阻塞"而闲置。
如果生产线上有缓冲区,当一台机器发生故障,其下游的机器可以利用两台机器之间缓冲区中的物料继续运作。如果这种情况持续足够长的时间,缓冲区会变空,该机器会"饥饿"。缓冲区越大,在机器"饥饿"之前的时间就越长。与此同时,故障机器的上一个缓冲区会增加物料,而其上游机器仍在工作。如果这种情况持续足够长的时间,缓冲区就会填满,上游机器会被"阻塞"。因此,缓冲区可以延缓闲置,从而提高生产率。较大的缓冲区更有效地解耦机器,因为它们能够吸收更大的中断;但这样做的代价是增加库存。
惠普打印机主生产线上的每台机器的加工时间都是9秒,既每小时400个。两条产线就是每小时800台打印机。设计时认为,就算设备效率为99%,每小时生产540台(大约相当于理想产能的67.5%)也一点儿问题也没有,每月大约685小时的可用生产时间(相当于每天工作23小时,看出来惠普也是拼了),估计该系统每月可以生产369,900台。这超过了每月30万台的设计目标。
显然,设计时过于乐观了,设备效率只有97%,实际产能大约为每月12.5万台。单纯考虑一台设备,97%的效率,每小时仍然远大于540台,当考虑了由于没有缓冲区,当一台设备故障时(3%的时间)其上下游的所有设备均因"饥饿"或"阻塞"停止生产,整条产线和效率快速下降。
缓冲区的合适大小
尽管增加缓冲区会增加库存成本,设置缓冲区仍是最高效的解决方案,问题的关键是面对月产30万台的目标增加多少缓冲区最合适。
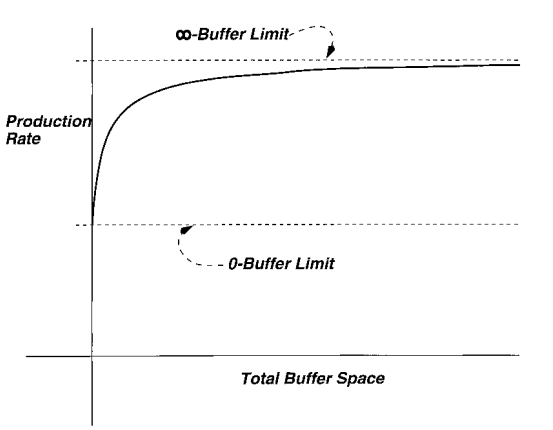
图2: 缓冲区与生产效率关系图
由缓冲区与生产效率关系图可见,没有缓冲区或缓冲区大小为0时,生产线效率最低,随着缓冲区中物料的增加,生产效率快速提升,当达到一定数量后,增大缓冲区的大小对生产效率的提升就非常有限了。考虑缓冲区中的物料会每出一个就会同时再进一个,过多的缓冲物料相当于长时间滞留在缓冲区,成本很高。
假设一条生产线有 k 台机器,这些机器的运行时间相等且恒定。第一台机器永远不会"饥饿",最后一台机器永远不会"阻塞"。操作时间被选择为时间单位。机器只能在工作时发生故障。机器 Mi 在工作时单位时间内发生故障的概率为 p i p_i pi,机器 M i M_i Mi 在停机状态下单位时间内修复的概率为 r i r_i ri。
我们定义 F i = 1 / f i F_i=1/f_i Fi=1/fi 和 R i = 1 / r i R_i=1/r_i Ri=1/ri,分别表示平均故障时间和平均修复时间。
缓冲区大小为零的生产线在各个阶段之间没有解耦。因此,一旦任何一台机器发生故障,整条生产线将被迫等待。基于这些假设,Buzacott [1967] 证明了一个好的生产线效率的近似值为
E = 1 1 + ∑ i = 1 k f i r i = 1 1 + ∑ i = 1 k R i F i E=\frac{1}{1+\sum_{i=1}^k\frac{f_i}{r_i}}=\frac{1}{1+\sum_{i=1}^{k}\frac{R_i}{F_i}} E=1+∑i=1krifi1=1+∑i=1kFiRi1
实际上,每台机器的工作区域都像是一个容量为1的缓冲区。然而,我们认为使用 Buzacott 的近似方法是合适的,因为操作时间相对于故障时间来说很短。生产线的效率是生产的部件数量与如果没有故障情况下应生产的部件数量的比率。在这里,效率与生产率相同,因为它测量了每单位时间生产的平均部件数量。Buzacott 和 Shanthikumar [1993] 将这个公式推广到了包含不同操作时间的系统。
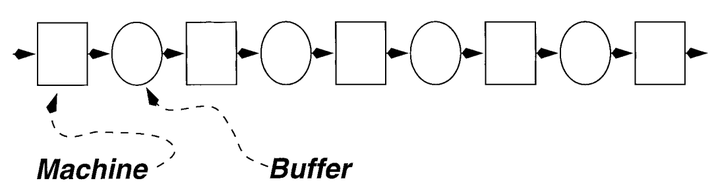
图3:在这个生产线的表示中,方形代表机器,圆形代表缓冲区。物料按所示方向从机器移动到临时存储缓冲区再到机器。机器会在随机时间发生故障,并会停机随机时间长度。缓冲区是有限的,因此中断会以"饥饿"和"阻塞"的形式向两个方向传播。由于其行为的复杂性,这个系统只能通过模拟或分解近似来评估。
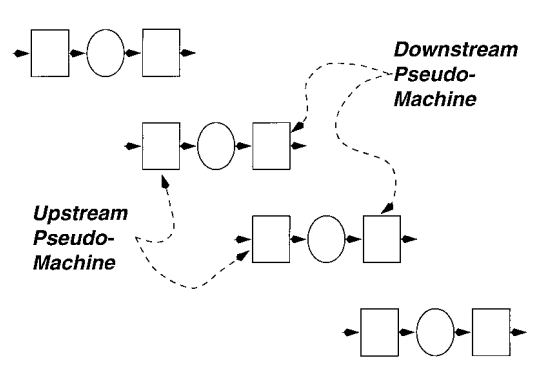
同步模型生产线的分解 图3显示了一个五台机器、四个缓冲区的生产线。对于一个所有机器具有恒定且相等的操作时间,并且修复和故障时间呈几何分布的系统,Gershwin [1987] 表明,生产率和平均在制品库存可以通过一组两台机器的生产线来近似表示(见图4)。
至此,原文已经完成对惠普生产线效率问题的描述与分析,给出了解决问题的构想:添加在制品库。文章的下半部分是关于计算在制品库大小过程中对引文的分析,可能是考虑商业机密,原文中并没有给出详细的解决方案。为了方便学习,我还是将原文翻译以供参考。
在本系列的后续文章中,我会逐渐展开对相关算法的介绍与分析。如果你觉得本文描述的问题恰好与你正在面临的生产问题有某些相似性,而且不想花时间进行深入的数学研究,也可以私信我,我们公司愿意提供具体的分析服务。
每个两台机器的生产线都构建了一个与原生产线中某个缓冲区大小相同的缓冲区。选择机器的方式是使得缓冲区中的观察者只能看到到达和离开的过程,这与原生产线中对应缓冲区的观察者看到的过程几乎相同。Gershwin [1987] 推导出了确定机器参数的方程式;Dallery、David 和 Xie [1988] 提供了一种高效的算法来求解这些方程(称为 DDX 算法)。Gershwin [1994] 对此进行了描述。
我们在惠普打印机生产线项目早期阶段使用了这个算法。其优势在于速度。用个人计算机分析一条生产线只需不到一秒的时间,而编写模拟程序可能需要数月时间,运行模拟可能需要数小时。如此长的时间使得模拟在分析和设计中变得笨拙。这个方法是一个近似值。较大系统中物料进入和离开缓冲区的实际行为与两台机器生产线中的物料行为有微妙的不同。对于那些机器之间平均故障时间或平均修复时间非常不同的系统,这种差异会加大。
连续材料模型的生产线分解
由于惠普打印机生产线中的机器操作时间不同,我们需要一个更好的近似值。然而,扩展 Gershwin [1987] 到具有不同确定性处理时间的机器系统似乎难度过大,因此 Burman [1995] 使用了 Gershwin 和 Schick [1980] 提出的连续材料两台机器生产线模型,进行了类似的分解,用于具有连续材料和不同处理速率的长生产线。(不同的处理速率使得分解方程的推导比早期系统更为复杂。)他还为这种情况改编了 DDX 算法,并将其称为 ADDX 算法。这个新算法同样极其快速。
装配-拆卸系统的连续物料模型的分解
由于惠普的生产系统包括装配过程,我们需要的不仅仅是用于生产线的 ADDX 算法。因此,Gershwin 和 Burman [1997] 扩展了 ADDX 算法(以及 Gershwin [1991] 早期为同步系统开发的装配-拆卸系统工作和 Di Mascolo、David 和 Dallery [1991] 为具有相同处理速率的连续材料系统所做的工作),用于具有连续材料和不同处理速率的装配-拆卸系统。同样,该算法再次证明了其快速和实用性。它已经实现了图形用户界面,并且惠普正在将其作为设计新打印机生产系统的标准方法的一部分加以使用。
参考文献
Bonvik, A. M. 1996, "Performance analysis of manufacturing systems under hybrid control policies," PhD thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts.
Burman, M. 1995, "New results in flow line analysis," PhD thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts.
Buzacott, J. A. 1967, "Automatic transfer lines with buffer stocks," International Journal of Production Research, Vol. 5, No. 3, pp. 183-- 200.
Buzacott, J. A. and Shanthikumar, J. G. 1993, Stochastic Models of Manufacturing Systems,Prentice Hall, Englewood Cliffs, New Jersey.
Dallery, Y.; David, R.; and Xie, X.-L. 1988, "An efficient algorithm for analysis of transfer lines with unreliable machines and finite buffers," IIE Transactions, Vol. 20, No. 3 (September), pp. 280--283.
Dallery, Y. and Gershwin, S. B. 1992, "Manufacturing flow line systems: A review of models and analytical results," Queueing Systems Theory and Applications, Special Issue on Queueing Models of Manufacturing Systems, Volume 12, No. 1--2 (December), pp. 3--94.
Di Mascolo, M.; David, R.; and Dallery, Y. 1991, "Modeling and analysis of assembly systems with unreliable machines and finite buffers," IIE Transactions, Vol. 23, No. 4 (December), pp. 315--331.
Gershwin, S. B. 1987, "An efficient decomposition method for the approximate evaluation of tandem queues with finite storage space and blocking," Operations Research, Vol. 35, No. 2 (March--April), pp. 291--305.Gershwin, S. B. 1991, "Assembly/disassembly systems: An efficient decomposition algorithm for tree-structured networks," IIE Transactions, Vol. 23, No. 4 (December), pp. 302--314.
Gershwin, S. B. 1994, Manufacturing Systems Engineering, Prentice Hall, Englewood Cliffs, New Jersey.
Gershwin, S. B. and Burman, M. H. 1997, "Decomposition equations and algorithm for A/D systems---Derivation of equations," working paper.
Gershwin, S. B. and Schick, I. C. 1980, "Continuous model of an unreliable two-stage material flow system with a finite interstage buffer," Massachusetts Institute of Technology Laboratory for Information and Decision Systems Report LIDS-R-1039, September.
本文是 MIT 工业工程专栏的一部分,先放出来,想看看大家是否对此感兴趣,并听听评价,0. AI 时代的制造领域核心竞争力:MITx 制造原理系列课程介绍
在AI 时代,可能并不需要如此深入地了解这些公式的来源,只是这些基本概念与常识就是与AI 聊天的提示词
如果你对智能制造感兴趣,关注我,第一时间获取与AI 交流的提示词。