leetcode打卡 - 技术栈

1 动态规划-字符串公共子序列

计算使两个字符串相等所需删除字符的最小 ASCII 值之和，核心思路是动态规划。

可以将问题转化为寻找两个字符串的公共子序列，使得这个子序列的 ASCII 值之和最大

解题思路

定义 dp[i][j] 表示使 s1 的前 i 个字符和 s2 的前 j 个字符相等所需的最小删除 ASCII 和。状态转移如下：

如果 s1[i-1] == s2[j-1]，当前字符可以保留，不需要删除，即 dp[i][j] = dp[i-1][j-1]。
否则，可以删除 s1[i-1] 或 s2[j-1]，取两者中代价较小的：
dp[i][j] = min(dp[i-1][j] + ord(s1[i-1]), dp[i][j-1] + ord(s2[j-1]))。

初始化边界条件：

dp[0][j]：s1 为空，需要删除 s2 的所有前 j 个字符，即累加 s2 的 ASCII 值。
dp[i][0]：s2 为空，需要删除 s1 的所有前 i 个字符，即累加 s1 的 ASCII 值。

最终答案为 dp[n][m]，其中 n 和 m 分别为 s1 和 s2 的长度

遇到的问题

1.dp递归方程不理解

2.dp矩阵下标与字符串下标的区别

3.初始化边界

2 最大矩形-单调栈

python 复制代码

from typing import List

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if not matrix or not matrix[0]:
            return 0
        
        rows, cols = len(matrix), len(matrix[0])
        heights = [0] * cols
        max_area = 0
        
        # 遍历每一行
        for i in range(rows):
            # 更新高度数组
            for j in range(cols):
                if matrix[i][j] == '1':
                    heights[j] += 1
                else:
                    heights[j] = 0
            
            # 计算当前行的柱状图最大矩形面积
            max_area = max(max_area, self.largestRectangleArea(heights))
        
        return max_area
    
    def largestRectangleArea(self, heights: List[int]) -> int:
        """单调栈解法：计算柱状图中的最大矩形面积"""
        n = len(heights)
        stack = []  # 存储索引，保持索引对应的高度单调递增
        max_area = 0
        
        # 遍历所有柱子，末尾添加一个高度为0的虚拟柱子
        for i in range(n + 1):
            # 当前柱子的高度（如果是最后一个虚拟柱子，高度为0）
            current_height = heights[i] if i < n else 0
            
            # 当前柱子高度小于栈顶柱子高度时，弹出栈顶并计算面积
            while stack and current_height < heights[stack[-1]]:
                # 弹出栈顶索引
                height = heights[stack.pop()]
                # 左边界：如果栈为空则为-1，否则为当前栈顶索引
                left = -1 if not stack else stack[-1]
                # 右边界：当前索引i
                width = i - left - 1
                # 计算面积并更新最大值
                max_area = max(max_area, height * width)
            
            # 当前柱子入栈
            stack.append(i)
        
        return max_area

3.切比雪夫距离

两点之间的距离 = max(dx, dy)

python 复制代码

class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        res = 0
        for i in range(len(points)-1):
            x0,x1 = points[i]
            y0,y1 = points[i+1]
            res+=max(abs(x0-y0),abs(x1-y1))
        return res

4.分割正方形

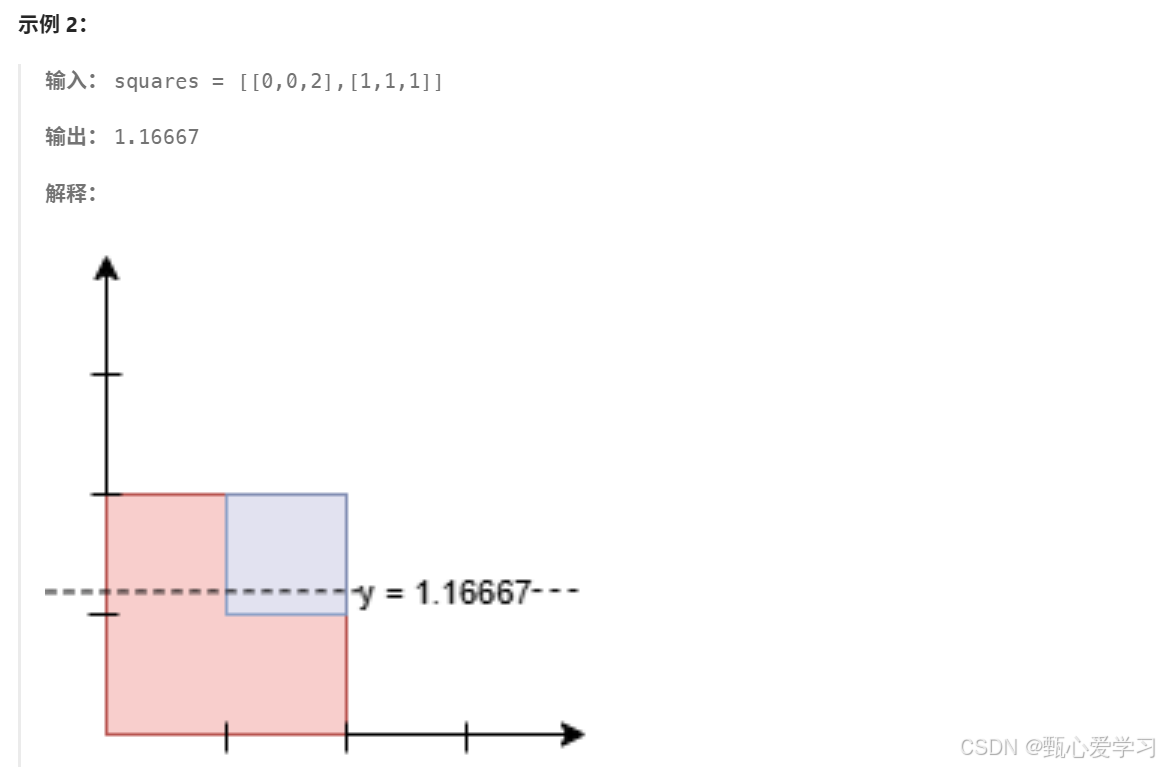
最小二分求解