力扣：1553. 吃掉 N 个橘子的最少天数（记忆化搜索，Dijkstra解法）

厨房里总共有 n 个橘子，你决定每一天选择如下方式之一吃这些橘子：

吃掉一个橘子。
如果剩余橘子数 n 能被 2 整除，那么你可以吃掉 n/2 个橘子。
如果剩余橘子数 n 能被 3 整除，那么你可以吃掉 2*(n/3) 个橘子。

每天你只能从以上 3 种方案中选择一种方案。

请你返回吃掉所有 n 个橘子的最少天数。

示例 1：

复制代码

输入：n = 10
输出：4
解释：你总共有 10 个橘子。
第 1 天：吃 1 个橘子，剩余橘子数 10 - 1 = 9。
第 2 天：吃 6 个橘子，剩余橘子数 9 - 2*(9/3) = 9 - 6 = 3。（9 可以被 3 整除）
第 3 天：吃 2 个橘子，剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。
第 4 天：吃掉最后 1 个橘子，剩余橘子数 1 - 1 = 0。
你需要至少 4 天吃掉 10 个橘子。

示例 2：

复制代码

输入：n = 6
输出：3
解释：你总共有 6 个橘子。
第 1 天：吃 3 个橘子，剩余橘子数 6 - 6/2 = 6 - 3 = 3。（6 可以被 2 整除）
第 2 天：吃 2 个橘子，剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。（3 可以被 3 整除）
第 3 天：吃掉剩余 1 个橘子，剩余橘子数 1 - 1 = 0。
你至少需要 3 天吃掉 6 个橘子。

示例 3：

复制代码

输入：n = 1
输出：1

示例 4：

复制代码

输入：n = 56
输出：6

提示：

1 <= n <= 2*10^9

思路1：记忆化搜索

这个题拿到手，一眼就能想到dfs搜索的解法，就是分3种情况 dfs(n-1), dfs(n/2), dfs(n/3)一直递归，直到n=0，对比递归次数获取最少次数，但是显然超限。

在做优化的过程中就自然想到了记忆化搜索，既然n可以向下递归到n-1，n/2，n/3，就说明吃掉n的最少天数依赖于n-1，n/2，n/3这3者的数值，那么就可以设置记忆化数组a，a[i]表示吃掉数量为i的橘子至少需要多少天。

之后就还是搜索，以当前橘子数量 num 为入参，自顶向下求解吃掉 n 个橘子的最少天数，

首先判断边界条件，直接返回缓存中预初始化的结果以终止递归；

接着查询缓存，若 num 已计算过则直接返回缓存值，避免重复递归计算；

之后通过状态转移方程计算最优解，即取「先花 num%2 天将 num 减到能被 2 整除，再执行吃一半操作并递归求解 num/2 的最少天数」和「先花 num%3 天将 num 减到能被 3 整除，再执行吃三分之二操作并递归求解 num/3 的最少天数」两条路径的最小值，同时加 1 天对应除法操作本身的耗时，且将计算结果存入缓存供后续使用；

最后返回当前 num 的最少天数，供上层递归回溯，整个过程通过稀疏缓存和高效除法路径选择，将时间复杂度优化到 O (log n)，可支持超大 n 输入且不超时。

AC代码：

记忆化搜索：

C++：

cpp 复制代码

//力扣：1553. 吃掉 N 个橘子的最少天数
//dfs+记忆化搜索
class Solution {
public:
    int dfs(unordered_map<int,int>& a, int num) {
        if (num <= 2) {
            return a[num];
        }
        if (a.count(num)) {
            return a[num];
        }
        a[num] = min(
            dfs(a, num / 2) + num % 2,
            dfs(a, num / 3) + num % 3
        ) + 1;

        return a[num];
    }
    int minDays(int n) {
        unordered_map<int,int> a;//记忆化数组
        a[0] = 0;
        a[1] = 1;
        a[2] = 2;
        return dfs(a, n);
    }
};

java：

java 复制代码

class Solution {
        public int dfs(int num,HashMap<Integer,Integer> a){
            if(num<=2){

                return num;
            }
            if(a.get(num)!=null){
                return a.get(num);
            }
             int k= Math.min(
                    dfs(num/2,a)+num%2,
                    dfs(num/3,a)+num%3
            )+1;
            a.put(num,k);
            return a.get(num);
        }
        public int minDays(int n) {
            HashMap<Integer,Integer> a=new HashMap();
            return dfs(n,a);
        }
    }

但是这里不能使用dp算法，O(n)的时间复杂度不能满足庞大的数据量

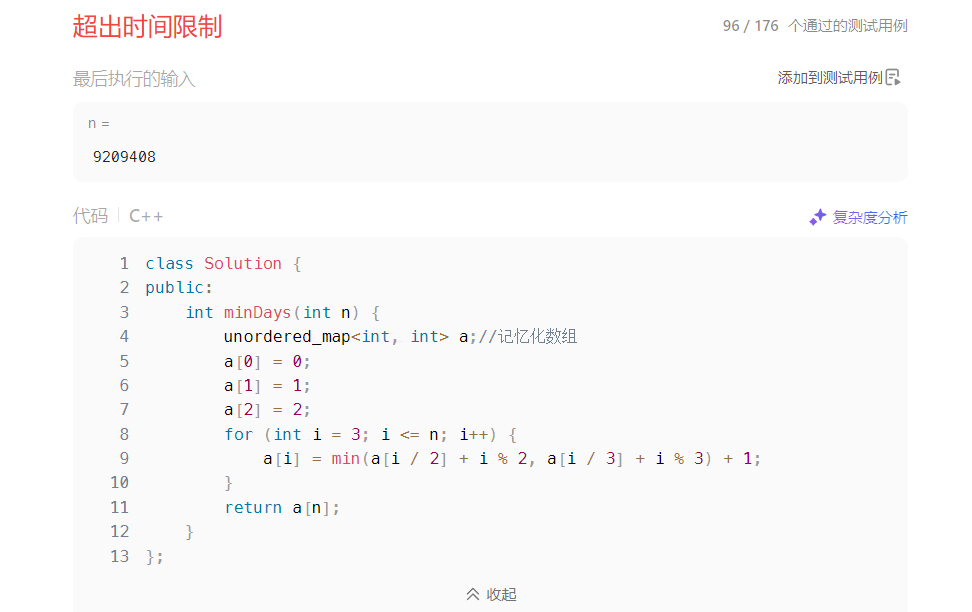
思路2：Dijkstra

与传统图论中Dijkstra不同的是，本题的Dijkstra更像是bfs。

可以设想在n到n/2之间存在一条长度为n%2+1的边，到n/3之间存在一条长度为n%3+1的边，求n到0的最短路。但是这里并不需要建图。

对于任意一个数量为n的节点，他的邻接节点就是n/2和n/3，因此，只要对这两个节点考虑做松弛入队即可。

之后就是常规的Dijkstra堆优化求解的过程

AC代码：

Dijkstra算法：

C++：

cpp 复制代码

class Solution {
public:
    //Dijkstra算法：
    //n到n/2之间存在一条长度为n%2+1的边
    // 到n/3之间存在一条长度为n%3+1的边
    //最短路径即为最少次数
    void Dijkstra(unordered_map<int, int>& dist, int n) {
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
        q.push({ 0,n });
        dist[n] = 0;
        while (!q.empty()) {
            auto it = q.top();
            q.pop();
            int w = it.first;
            int m = it.second;
            if (m <= 2) {
                if (!dist.count(0)) {
                    dist[0] = w + m;
                }
                else {
                    dist[0] = min(dist[0], w + m);
                }
                continue;
            }
            else {
                if (!dist.count(m / 2) || dist[m / 2] > w + (m % 2 + 1)) {
                    dist[m / 2] = w + (m % 2 + 1);
                    q.push({ dist[m / 2],m / 2 });
                }
                if (!dist.count(m / 3) || dist[m / 3] > w + (m % 3 + 1)) {
                    dist[m / 3] = w + (m % 3 + 1);
                    q.push({ dist[m / 3],m / 3 });
                }
            }
        }
    }
    int minDays(int n) {
        unordered_map<int, int> dist;
        Dijkstra(dist, n);
        return dist[0];
    }
};

java：

java 复制代码

import java.util.HashMap;
import java.util.PriorityQueue;
import java.util.Map;
import java.util.AbstractMap;

class Solution {
    private void dijkstra(HashMap<Integer, Integer> dist, int n) {
        PriorityQueue<Map.Entry<Integer, Integer>> pq = new PriorityQueue<>(
            (a, b) -> a.getKey() - b.getKey()
        );
        
        pq.add(new AbstractMap.SimpleEntry<>(0, n));
        dist.put(n, 0);
        
        while (!pq.isEmpty()) {
            Map.Entry<Integer, Integer> cur = pq.poll();
            int w = cur.getKey();
            int m = cur.getValue();
            
            if (m <= 2) {
                int totalDays = w + m;
                if (!dist.containsKey(0)) {
                    dist.put(0, totalDays);
                } else {
                    dist.put(0, Math.min(dist.get(0), totalDays));
                }
                continue;
            }
            
            int target2 = m / 2;
            int cost2 = w + (m % 2 + 1);
            if (!dist.containsKey(target2) || cost2 < dist.get(target2)) {
                dist.put(target2, cost2);
                pq.add(new AbstractMap.SimpleEntry<>(cost2, target2));
            }
            
            int target3 = m / 3;
            int cost3 = w + (m % 3 + 1);
            if (!dist.containsKey(target3) || cost3 < dist.get(target3)) {
                dist.put(target3, cost3);
                pq.add(new AbstractMap.SimpleEntry<>(cost3, target3));
            }
        }
    }
    
    public int minDays(int n) {
        HashMap<Integer, Integer> dist = new HashMap<>();
        dijkstra(dist, n);
        return dist.get(0);
    }
}