1. 单值二叉树

单值二叉树指的是二叉树中存储的数据都是同一个值,那么该如何判断一个二叉树是否为单值二叉树呢?
利用递归的思想,将左子树和右子树中的数据分别与根节点中的数据进行比较,相同返回true,不同返回false,以此递归循环便可进行判断。
代码实现:
cpp
//判断是否为单值二叉树
bool isUnivalTree(BTNode* root)
{
if (root == NULL)
return true;//默认空树返回true
if (root->Left != NULL && root->Left->data != root->data)
return false;
if (root->Right != NULL && root->Right->data != root->data)
return false;
return isUnivalTree(root->Left) && isUnivalTree(root->Right);
}2. 检查两棵树是否相
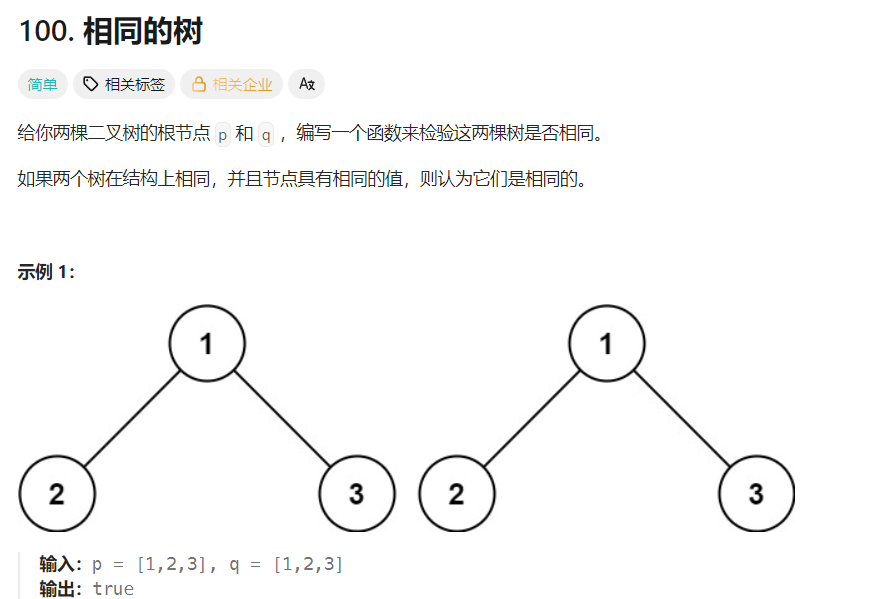
这个方法通过递归比较两棵二叉树的结构和节点值来判断是否相同,其核心思路如下:
终止条件:
- 若两节点均为空(
p == NULL && q == NULL),说明当前分支结构一致,返回true。- 若仅一节点为空(
p == NULL || q == NULL),说明结构不一致,返回false。节点值比较:
- 若当前节点值不同(
p->data != q->data),直接返回false。递归比较子树:
- 递归检查左子树(
p->Left和q->Left)和右子树(p->Right和q->Right)是否相同,只有两者均相同才返回true。
代码实现:
cpp
//检查两棵树是否相同
bool issameTree(BTNode* p, BTNode* q)
{
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
if (p->data != q->data)
return false;
return issameTree(p->Left, q->Left) &&
issameTree(p->Right, q->Right);
}3. 对称二叉树
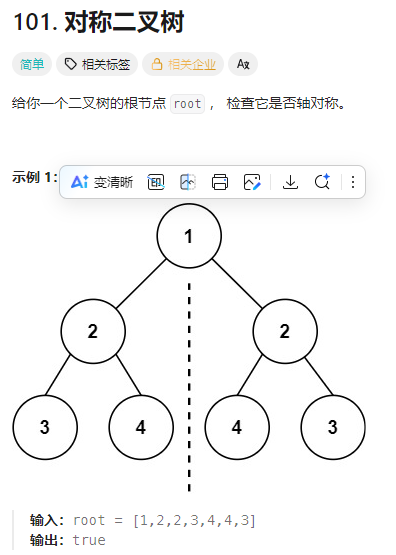
这题的思路和上一题的思路基本相同,只需要将这棵树的左右子树看作两棵树,然后对这两棵树的左子树和右子树进行比较即可。
算法思路
对称二叉树的定义:
- 一棵二叉树是对称的,当且仅当它的左子树和右子树互为镜像。
- 两棵树互为镜像的条件:
- 它们的根节点值相同。
- 一棵树的左子树与另一棵树的右子树互为镜像。
- 一棵树的右子树与另一棵树的左子树互为镜像。
递归实现:
- 定义一个辅助函数
_isSymmetric(p, q),用于递归比较两棵子树p和q是否互为镜像。- 在主函数
isSymmetric(root)中,调用_isSymmetric(root->Left, root->Right)比较根节点的左右子树。递归终止条件:
- 如果两棵子树均为空(
p == NULL && q == NULL),返回true。- 如果其中一棵子树为空而另一棵不为空(
p == NULL || q == NULL),返回false。- 如果两棵子树的根节点值不同(
p->data != q->data),返回false。递归比较:
- 比较
p的左子树和q的右子树(_isSymmetric(p->Left, q->Right))。- 比较
p的右子树和q的左子树(_isSymmetric(p->Right, q->Left))。- 只有两者都为真时,才返回
true。
代码实现:
cpp
bool _isSymmtric(BTNode* p, BTNode* q)
{
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
if (p->data != q->data)
return false;
return _isSymmtric(p->Left, q->Right)
&& _isSymmtric(p->Right, q->Left);
}
//对称二叉树的判断
bool isSymmtric(BTNode* root)
{
if (root == NULL)
return true;
return _isSymmtric(root->Left, root->Right);
}4. 判断一颗树是否和另一棵树的子树相同
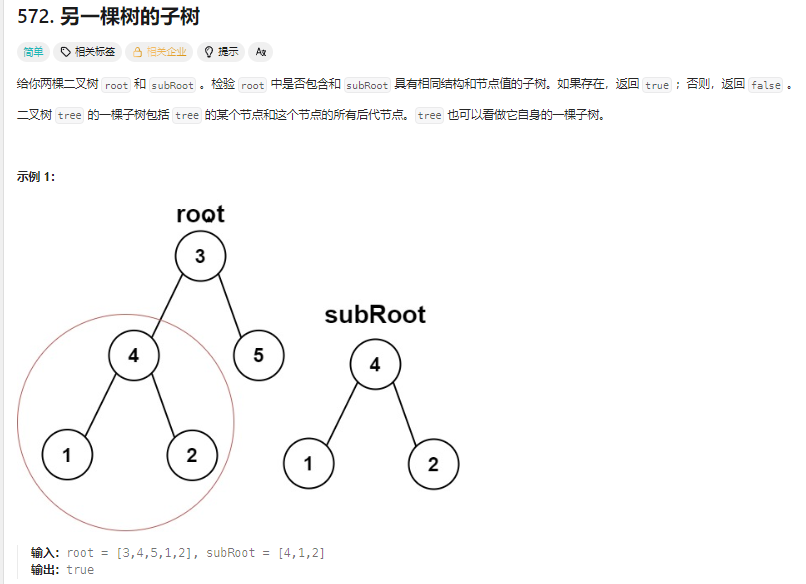
递归实现:
- 定义一个辅助函数
issameTree(p, q)(假设已实现),用于判断两棵树是否完全相同。- 在
isSubTree函数中:
- 如果
root为空(root == NULL),说明已经遍历完root但未找到匹配的子树,返回false。- 如果当前
root的节点值与subroot的根节点值相同,并且issameTree(root, subroot)返回true,则说明找到匹配的子树,返回true。- 否则,递归检查
subroot是否是root的左子树或右子树的子树。代码实现:
代码实现:
cpp
//判断一个树是否和另一棵树的子树相同
bool isSubTree(BTNode* root, BTNode* subroot)
{
if (root = NULL)
return false;
if (root->data == subroot->data && issameTree(root, subroot))
return true;
return isSubTree(root->Left, subroot)
|| isSubTree(root->Right, subroot);
}5. 前序遍历
这里所指的前序遍历和上一节说的有所不同,这里是指通过前序遍历的方式将数据的值存放到一个数组中,并返回这个数组。
代码实现:
cpp
//前序遍历二叉树,将数值存储到数组中并返回
//首先求得二叉树的总结点个数
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->Left) + TreeSize(root->Right) + 1;
}
//进行前序遍历及存储数据在数组中
void preOrder(BTNode* root,int* a,int* pi)
{
if (root == NULL)
return;
a[(*pi)++] = root->data;
preOrder(root->Left, a, pi);
preOrder(root->Right, a, pi);
}
//这个算法的主函数
int preorderTraversal(BTNode* root, int* returnsize)
{
*returnsize = Treesize(root);
int* a = (int*)malloc(sizeof(*returnsize));
int i = 0;
preOrder(root, a, &i);
return a;
}该算法通过递归前序遍历二叉树:先计算节点总数分配数组空间,再按根→左→右顺序存储节点值到数组,最后返回数组及元素个数
6. 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
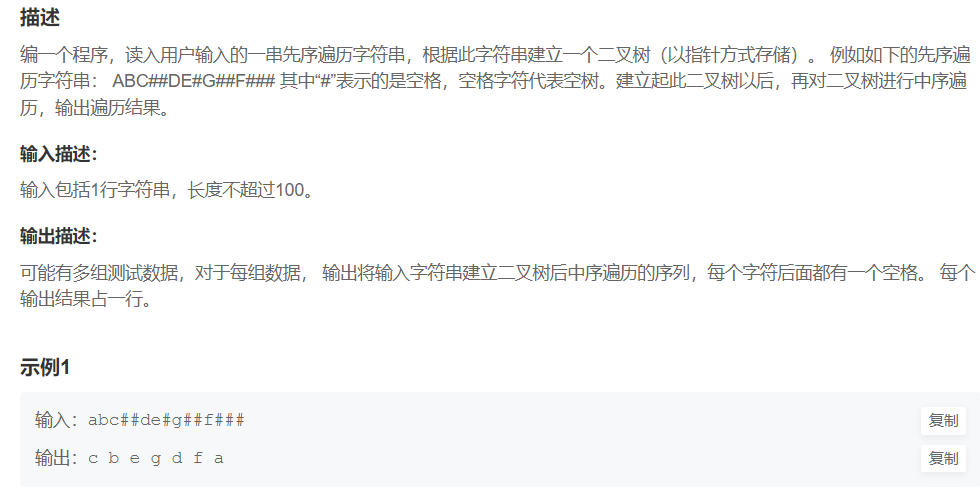
代码实现:
cpp
//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* TreeCreat(char* a, int* pi)
{
if (a[*pi] == '#')
//错误写法:if(a[(*pi)++] == '#')
//这种写法会导致代码走到这一步判断完条件语句之后自动加一,导致原来的字符被遗漏!
{
(*pi)++;
return NULL;//代表空树
}
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
root->data = a[(*pi)++];
root->Left = TreeCreat(a, pi);
root->Right = TreeCreat(a, pi);
return root;
}
int main()
{
char a[100];
scanf("%s ", a);
int i = 0;
BTNode* root = TreeCreat(a, &i);
return 0;
}这段代码通过前序遍历字符串 递归构建二叉树:遇到非
'#'字符时创建节点并递归构建左右子树,遇到'#'时返回NULL表示空节点,索引指针pi随递归动态移动确保字符顺序处理。
**注:**千万不能够写代码中的错误示范,因为如果那样写的话,当一个字符在进行判断时,假如不满足判断的条件语句,那i就会自动加1到下一个字符,这就导致原先的字符还没有被正确操作就被略过了,这是一个经典的错误!