机器学习-L1正则化和L2正则化解决过拟合问题

机器学习-L1正则化和L2正则化解决过拟合问题

在机器学习中，过拟合（Overfitting） 是模型训练过程中最常见且最棘手的问题之一。当一个模型在训练集上表现优异（误差极小），却在测试集或新数据上表现糟糕时，我们就说模型出现了过拟合。这种现象如同学生死记硬背 了所有习题答案，但遇到新题目就束手无策。本文将深入探讨过拟合的本质原因 、直观理解 ，并重点讲解两种强大的解决方案------L1正则化 和L2正则化，从数学原理到实际应用进行全面剖析。

什么是过拟合？

在开始正则化的讲解之前，我们首先要清楚过拟合的概念及其表现。模型拟合状态通常分为三种情况：

欠拟合（Underfitting）:

• 表现：模型在训练集和测试集上都表现不佳，预测误差都很大
• 原因：模型过于简单，无法捕捉数据中的基本规律
• 类比：只用直线去拟合明显是曲线的数据分布
• 解决思路：增加模型复杂度（如增加特征、使用更复杂的模型）

正好拟合（Just Fitting / Good Fit）:

• 表现：模型在训练集和测试集上都表现良好，泛化能力强
• 原因：模型复杂度与数据复杂度匹配得当
• 理想状态：模型既学习了数据中的普遍规律，又不过度关注噪声

过拟合（Overfitting）:

• 表现：模型在训练集上表现极好（误差接近0），但在测试集上表现很差
• 原因：模型过于复杂，过度学习了训练数据中的噪声和偶然特征
• 类比：学生不仅记住了知识点，还把练习册上的印刷错误也背下来了
• 危险：模型失去了泛化能力，在实际应用中会失败

为了更好地理解这三种状态，让我们通过一个简单的例子来可视化它们。

可视化理解三种拟合状态

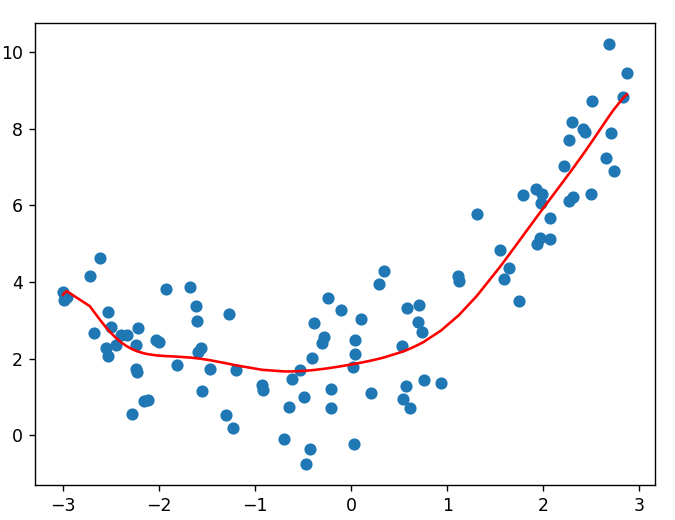
假设我们有一组真实数据，它们本应遵循一个二次函数关系：y=0.5x2+x+2y = 0.5x^2 + x + 2y=0.5x2+x+2，但由于现实世界的各种因素，实际观测值会带有一定的随机噪声。因此我们利用numpy生成一组随机数带充当随机噪声：

# 随机生成x轴 100个数据, 模拟: 特征.
x = np.random.uniform(-3, 3, 100)
# 基于x轴值, 通过线性公式, 生成y轴 100个数据, 模拟: 标签.
# 线性公式: y = kx + b = 0.5 * x ** 2 + x + 2 + 噪声
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, 100)

欠拟合的情况

当我们使用一个过于简单的模型（如线性模型 y=wx+by = wx + by=wx+b）去拟合这些数据时：

# 使用简单线性模型拟合二次数据
estimator = LinearRegression()
estimator.fit(X_linear, y)  # X_linear只有一维特征

结果会怎样呢？模型试图用一条直线去拟合明显弯曲的数据点，就像用尺子去测量弯曲的河流长度，必然会丢失大量信息。训练误差和测试误差都会很大，因为模型连数据的基本趋势都没能捕捉到。

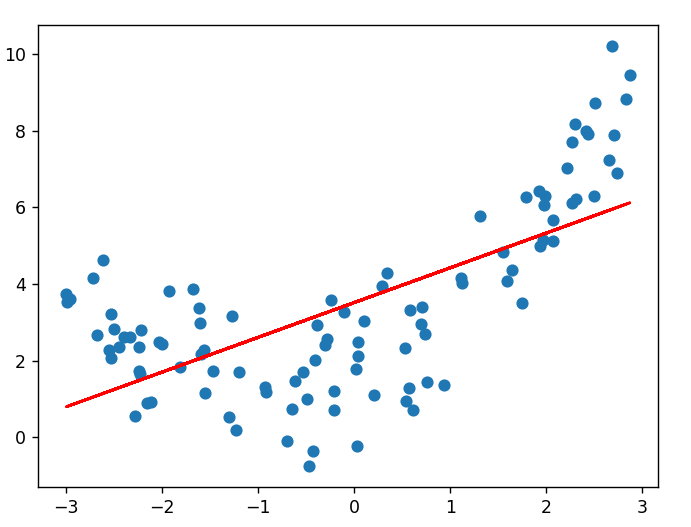
从数学角度看，欠拟合模型的 偏差（Bias） 很大，因为它对真实规律的假设过于简化。在损失函数曲面上，欠拟合的模型参数可能停留在某个局部高点，没有到达真正的谷底。

正好拟合的情况

当我们增加模型复杂度，使用二次模型 y=w1x+w2x2+by = w_1x + w_2x^2 + by=w1x+w2x2+b 去拟合这些数据时：

# 使用二次特征拟合二次数据
X_quadratic = np.hstack([X, X**2])  # 增加二次特征
estimator.fit(X_quadratic, y)

这时模型复杂度与数据真实复杂度匹配了。模型能够很好地捕捉数据的真实规律：既学到了二次函数的弯曲特性，又不会过度关注随机噪声。训练误差和测试误差都会比较小，且两者相差不大。

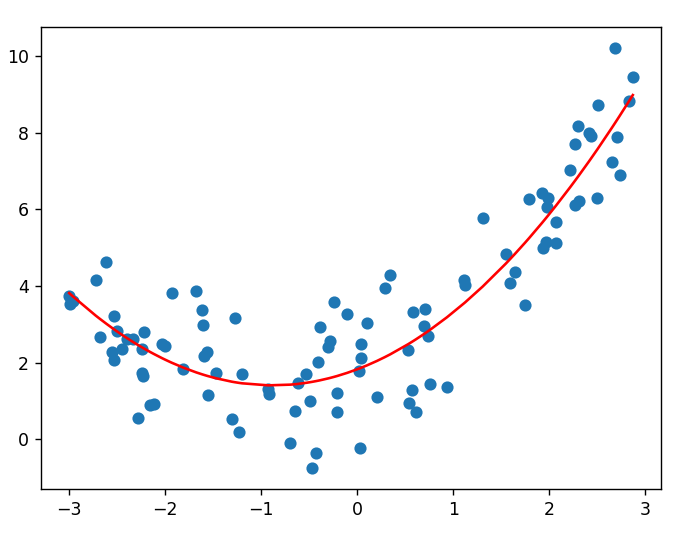
这种状态下，模型的**偏差-方差权衡（Bias-Variance Tradeoff）**达到了最佳平衡点。偏差足够小以捕捉主要规律，方差也不至于太大而过度拟合噪声。

过拟合的情况

当我们过度增加模型复杂度，使用十次多项式 y=∑i=110wixi+by = \sum_{i=1}^{10} w_i x^i + by=∑i=110wixi+b 去拟合这些数据时：

# 使用十次多项式拟合二次数据
X_poly = np.hstack([X, X**2, X**3, X**4, X**5, X**6, X**7, X**8, X**9, X**10])
estimator.fit(X_poly, y)

模型变得过于复杂，有太多的参数需要学习。这时模型不仅学会了二次函数的规律，还试图去拟合每一个数据点的随机波动（包括噪声）。结果就是模型在训练集上几乎完美（误差极小），但对新数据的预测效果很差。

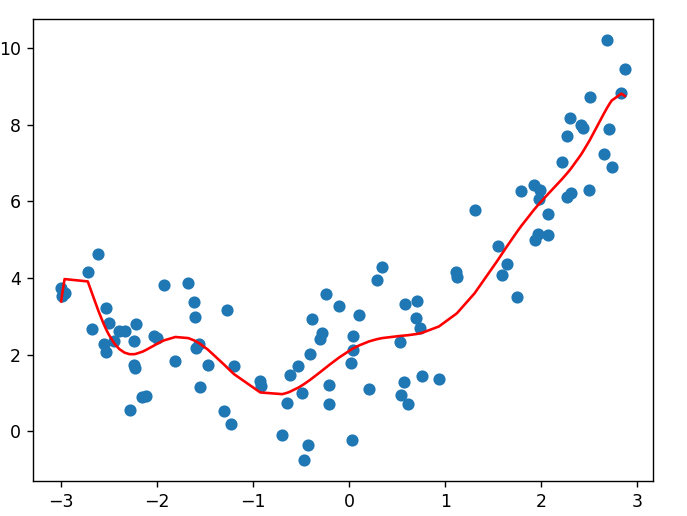
从图中可以看到，拟合曲线为了经过每一个训练数据点，变得极其曲折蜿蜒。它记住了每一个训练样本的细节，包括噪声，却丢失了数据的整体趋势。

过拟合的数学本质

要深入理解正则化，我们需要从数学角度分析过拟合的产生机制。

参数过多与模型容量

在多元线性回归中，我们有模型：y=w1x1+w2x2+⋯+wpxp+by = w_1x_1 + w_2x_2 + \dots + w_px_p + by=w1x1+w2x2+⋯+wpxp+b

当特征数量 ppp 很大，特别是相对于样本数量 nnn 很大时（p≈np \approx np≈n 或 p>np > np>n），模型就有了足够的"自由度"去拟合训练数据中的任何模式，包括噪声。这就是模型容量（Model Capacity） 过大导致的过拟合。

损失函数的最小化陷阱

回忆我们之前的损失函数（以均方误差为例）：
L(w)=1n∑i=1n(yi−yi)2∗L∗(∗w∗)=∗n∗1∑∗i∗=1∗n∗(∗y∗∗i∗−∗y∗∗i∗)2 L(w)=1n∑i=1n(yi−y^i)2*L*(*w*)=*n*1∑*i*=1*n*(*y**i*−*y*^*i*)2 L(w)=1n∑i=1n(yi−yi)2∗L∗(∗w∗)=∗n∗1∑∗i∗=1∗n∗(∗y∗∗i∗−∗y∗∗i∗)2

在没有约束的情况下，最小化这个损失函数可能会驱使某些权重 wiw_iwi 变得非常大，特别是当对应的特征 xix_ixi 与噪声高度相关时。这些大权重的特征虽然降低了训练误差，却损害了模型的泛化能力。

正则化：给模型加上"约束"

正则化的核心思想是：在最小化损失函数的同时，对模型参数施加某种约束或惩罚，防止它们变得过大。这就好比给一匹野马套上缰绳，既让它奔跑，又不让它失控。

正则化的一般形式是在原始损失函数基础上增加一个正则化项：
L正则化(w)=L原始(w)+λR(w)∗L∗正则化(∗w∗)=∗L∗原始(∗w∗)+∗λ∗∗R∗(∗w∗) L正则化(w)=L原始(w)+λR(w)*L*正则化(*w*)=*L*原始(*w*)+*λ**R*(*w*) L正则化(w)=L原始(w)+λR(w)∗L∗正则化(∗w∗)=∗L∗原始(∗w∗)+∗λ∗∗R∗(∗w∗)

其中：

• λ\lambdaλ 是正则化系数，控制正则化的强度
• R(w)R(w)R(w) 是正则化项 ，对参数 www 进行惩罚

不同的正则化项 R(w)R(w)R(w) 对应不同的正则化方法，最常用的就是L1正则化和L2正则化。

L1正则化（Lasso回归）

直观理解

想象你要去登山，背包空间有限。你需要选择带哪些物品：登山杖、水、食物、雨伞、备用鞋子等。L1正则化就像是一个严格的筛选器，它会迫使你放弃一些不是绝对必要的物品，只保留最重要的几样。

在机器学习中，L1正则化会迫使一些不重要的特征的权重变为0，从而实现特征选择（Feature Selection）。

数学形式

L1正则化在损失函数中增加的是权重的绝对值之和：
LL1(w)=L原始(w)+λ∑i=1p∣wi∣∗L∗L1(∗w∗)=∗L∗原始(∗w∗)+∗λ∗∑∗i∗=1∗p∗∣∗w∗∗i∗∣ LL1(w)=L原始(w)+λ∑i=1p∣wi∣*L*L1(*w*)=*L*原始(*w*)+*λ*∑*i*=1*p*∣*w**i*∣ LL1(w)=L原始(w)+λ∑i=1p∣wi∣∗L∗L1(∗w∗)=∗L∗原始(∗w∗)+∗λ∗∑∗i∗=1∗p∗∣∗w∗∗i∗∣

这里 λ∑i=1p∣wi∣\lambda \sum_{i=1}^p |w_i|λ∑i=1p∣wi∣ 就是L1正则化项。λ\lambdaλ 越大，对权重的惩罚越重，更多的权重会被压缩到0。

实际应用

在Python的scikit-learn库中，L1正则化通过Lasso回归实现：

from sklearn.linear_model import Lasso

# 创建L1正则化模型，alpha就是正则化系数λ
estimator = Lasso(alpha=0.1)  # alpha越大，正则化越强
estimator.fit(X, y)

# 训练后，查看权重
print("权重向量:", estimator.coef_)

你会发现，许多特征的权重都变成了0或接近0。这正是L1正则化的特征选择能力。拟合情况也会得到非常好的改善：

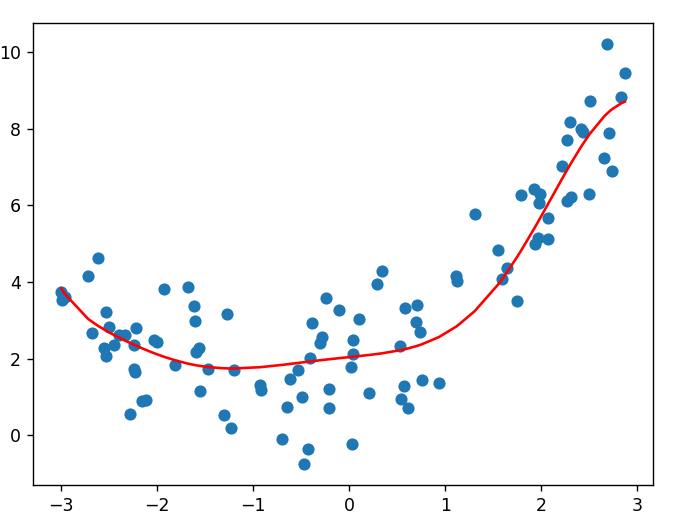
特点总结

1. 产生稀疏解：许多权重恰好为0
2. 自动特征选择：可以识别并剔除不重要的特征
3. 计算相对复杂：因为绝对值函数在0点不可导
4. 适合特征选择场景：当特征数量很多，但只有少数特征真正重要时

L2正则化（Ridge回归）

直观理解

继续登山的比喻，L2正则化不是让你丢弃物品，而是给你一个更大的背包。所有的物品都可以带上，但每件物品都必须"压缩"一下以减少占用空间。没有物品会被完全丢弃，但所有物品的"体积"（权重）都变小了。

数学形式

L2正则化在损失函数中增加的是权重的平方和：
LL2(w)=L原始(w)+λ∑i=1pwi2∗L∗L2(∗w∗)=∗L∗原始(∗w∗)+∗λ∗∑∗i∗=1∗p∗∗w∗∗i∗2 LL2(w)=L原始(w)+λ∑i=1pwi2*L*L2(*w*)=*L*原始(*w*)+*λ*∑*i*=1*p**w**i*2 LL2(w)=L原始(w)+λ∑i=1pwi2∗L∗L2(∗w∗)=∗L∗原始(∗w∗)+∗λ∗∑∗i∗=1∗p∗∗w∗∗i∗2

这里 λ∑i=1pwi2\lambda \sum_{i=1}^p w_i^2λ∑i=1pwi2 就是L2正则化项。同样，λ\lambdaλ 控制正则化的强度。

实际应用

在scikit-learn中，L2正则化通过Ridge回归实现：

from sklearn.linear_model import Ridge

# 创建L2正则化模型
estimator = Ridge(alpha=10.0)  # alpha越大，正则化越强
estimator.fit(X, y)

# 训练后，查看权重
print("权重向量:", estimator.coef_)

你会发现，所有权重都变小了，但几乎没有权重会恰好为0。

特点总结

1. 权重收缩：所有权重都变小，但不会为0
2. 稳定解：对数据中的噪声和异常值更稳健
3. 计算简单：平方项处处可导，优化更容易
4. 适合多重共线性场景：当特征高度相关时，L2正则化能提供更稳定的解