第三章：聚类算法

什么是聚类？

[第一部分：K-MEANS 算法 ------ 简单粗暴的经典](#第一部分：K-MEANS 算法 —— 简单粗暴的经典)

[1. 核心原理](#1. 核心原理)

[2. 工作流程](#2. 工作流程)

[3. 优缺点分析](#3. 优缺点分析)

[第二部分：DBSCAN 算法 ------ 基于密度的探索者](#第二部分：DBSCAN 算法 —— 基于密度的探索者)

[1. 核心概念](#1. 核心概念)

[2. 算法工作流程](#2. 算法工作流程)

[3. 参数选择技巧](#3. 参数选择技巧)

[4. 优缺点分析](#4. 优缺点分析)

总结

在机器学习的世界里，并非所有任务都有现成的"标准答案"（标签）。当我们面对一堆杂乱无章的数据，想要挖掘其内在规律时，聚类（Clustering）就是我们手中的瑞士军刀。

什么是聚类？

简单来说，聚类属于无监督学习（Unsupervised Learning），意味着我们手里没有标签。我们的目标是将相似的东西分到一组，让组内的差异尽可能小，组间的差异尽可能大。

聚类的难点通常在于：我们如何评估聚类的好坏？以及如何调整参数以获得最佳结果。

第一部分：K-MEANS 算法 ------ 简单粗暴的经典

K-MEANS 是最著名的聚类算法之一，它的核心思想非常直观：通过迭代寻找数据的"中心"。

1. 核心原理

K值的设定：K-MEANS 最大的特点（也是限制）是你必须先告诉算法要把数据分成几个簇（即指定 K 值）。
质心（Centroid）：每个簇的中心点就是该簇内所有点的均值（向量各维取平均）。
距离度量 ：算法通过计算距离来判断相似度，最常用的是欧几里得距离，有时也用余弦相似度（需先标准化）。

优化目标：

K-MEANS 试图让所有点到其所属簇质心的距离平方和最小。公式如下：

2. 工作流程

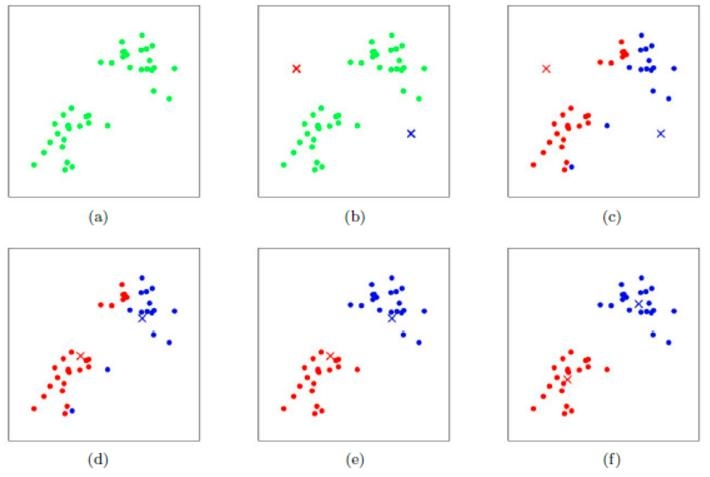
K-MEANS 的逻辑通常是：

随机初始化 K 个质心。
将每个样本点分配到最近的质心。
重新计算每个簇的质心（取平均值）。
重复步骤 2 和 3，直到质心不再变化或达到收敛条件。

3. 优缺点分析

优势：

算法简单，运行速度快。
非常适合处理常规的、球状分布的数据集。

劣势：

K值难确定：很多时候我们并不知道数据该分几类。
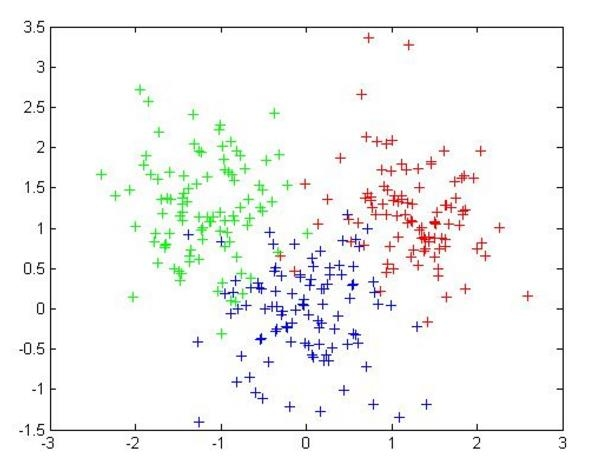
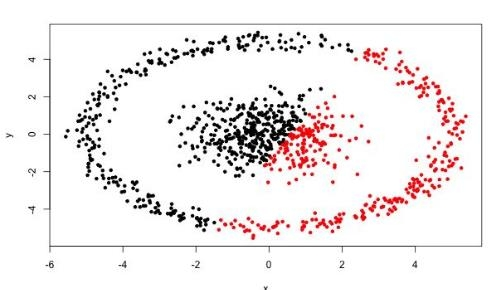
对形状敏感：很难发现任意形状的簇（比如环形、月牙形），它倾向于发现球状簇。
复杂度与样本量呈线性关系，处理超大规模数据时可能有压力。

第二部分：DBSCAN 算法 ------ 基于密度的探索者

为了解决 K-MEANS 无法处理复杂形状的问题，DBSCAN (Density-Based Spatial Clustering of Applications with Noise) 应运而生。它的理念不再是"距离中心最近"，而是"因为即使我们离得近，如果你周围很冷清，那你可能只是个噪声"。

1. 核心概念

DBSCAN 通过密度来定义簇。理解它需要掌握以下几个概念：

核心对象 (Core Object) ：如果一个点周围（邻域内）的"邻居"数量达到了设定的阈值（），那么这个点就是核心点。
-邻域 ()：就是我们设定的扫描半径。
直接密度可达 ：如果你在我的半径内，且我是核心点，那你就可以被我"直接密度可达" 。
密度可达：这是直接可达的"传播"版。比如 A 到 B 可达，B 到 C 可达，那么 A 到 C 就是密度可达的。
密度相连：若从某核心点出发，点 p 和点 q 都是密度可达的，则称它们密度相连。

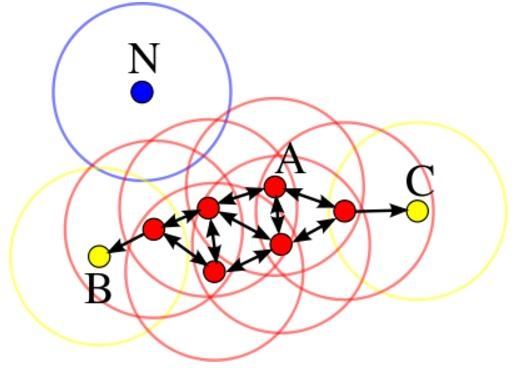
基于这些定义，DBSCAN 将点分为三类：

核心点：稠密区域内部的点。
边界点：属于某个簇，但不在核心区域（周围不够稠密），不能继续发展下线。
噪声点（离群点）：不属于任何簇，从任何核心点出发都无法到达它。

2. 算法工作流程

DBSCAN 的运行逻辑像是一种"病毒式扩散" ：

标记所有对象为未访问 (unvisited)。
随机选择一个未访问对象。
如果 $p$ 的邻域内至少有个对象：
- 创建一个新簇，把放进去。
- 把邻域内的所有点都拉进这个簇。
- 对于这些新加入的点，如果它们也是核心点，就继续去拉它们的邻居（密度可达的传播）。
如果的邻域内点太少，将其标记为噪声（虽然后续可能会被其他核心点"甚至"回来）。
重复直到所有点都被访问过。

3. 参数选择技巧

DBSCAN 有两个关键参数，选对了效果拔群，选错了效果很差：

半径：可以利用 K-距离 (K-distance) 图来辅助选择。计算每个点到第 k 个最近邻居的距离并排序，寻找图中的突变点（拐点）作为半径值。
MinPts：即 K-距离中的 k 值，一般取得比较小，需要多次尝试。

4. 优缺点分析

优势：

不需要指定簇个数：它自己会算出来有多少个簇。
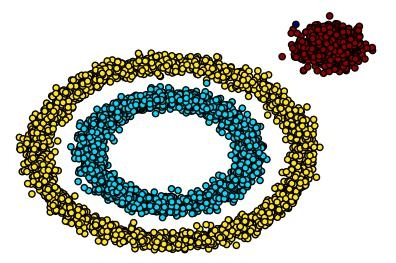
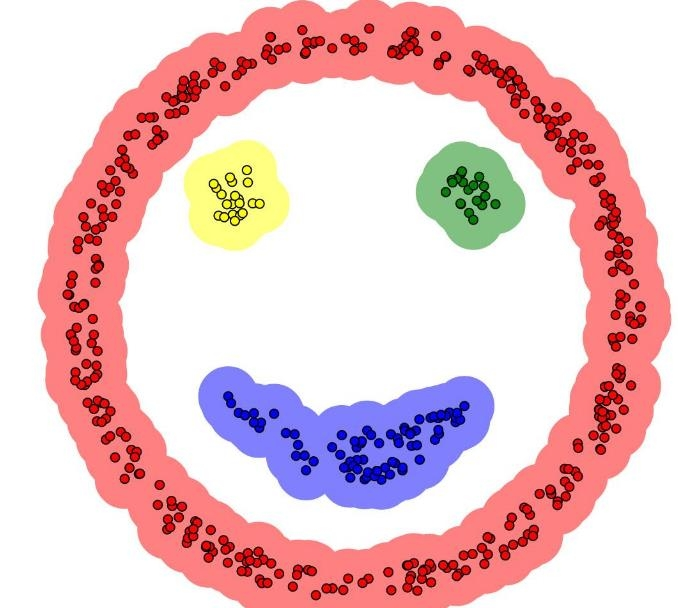
形状自适应：可以发现任意形状的簇（比如两个嵌套的圆环）。
抗噪能力：擅长找到并剔除离群点（噪声）。

劣势：

高维数据困难：在高维空间中，距离变得不再敏感（维数灾难），建议先做降维。
参数敏感 ：和对结果影响非常大，且难以选择。
效率问题：在 Sklearn 的实现中效率可能较慢，需要数据削减策略。

总结

如果你需要快速处理常规数据，且大概知道分几类，K-MEANS 是首选。
如果你的数据形状复杂（如地理位置、图像分割），或者你需要检测异常值，DBSCAN 是更好的选择。