第24章—数据结构篇：skiplist原理与实现解析

Redis 五大数据类型中有一种叫作 Sorted Set （有序集合）的类型，也经常被简称为"ZSet"。

ZSet 与我们常见的 Set 有一些类似，比如，Set 和 ZSet 里面存储的元素都不能重复。但是， ZSet 中的每个元素都会关联一个 double 类型的分数值（也称为 score），所有元素会按照 score 值的大小进行排序，这就是说 ZSet 是一个有序集合的原因。

在本节中，我们就从 ZSet 的底层存储开始，一步步抽丝剥茧，详细分析 Redis 中 ZSet 的核心原理和实现。

skiplist 基本概念

Redis 底层使用 跳跃表（skiplist） 这一数据结构作为 ZSet 的底层核心存储，当然，在一定条件下，Redis 会用 listpack 来优化 ZSet，在后面介绍 redisObject 的时候我们会单独拿出一节来详细讲解各个数据结构底层的这种优化。

skiplist 是基于随机算法的一种有序链表，其查询效率与红黑树的查询效率差不多，都是 O(logn)，但是 skiplist 的结构远比复杂的红黑树简单很多。下面我们就深入介绍一下 skiplist 的结构。

我们常见的有序链表结构如下图所示，每个节点里面有两个关键部分，一个是存放的数据，还有一个是指向下一个节点的 next 指针。

假设要在这个链表里面查询 48 这个节点，我们需要从 header 节点开始向后遍历，每遍历到一个节点，都要比较节点存储的值与 48 是否一致。最差的情况就是遍历完整个链表，时间复杂度也就是 O(N)。

skiplist 在普通有序链表的基础之上，添加多层有序链表，如下图所示：

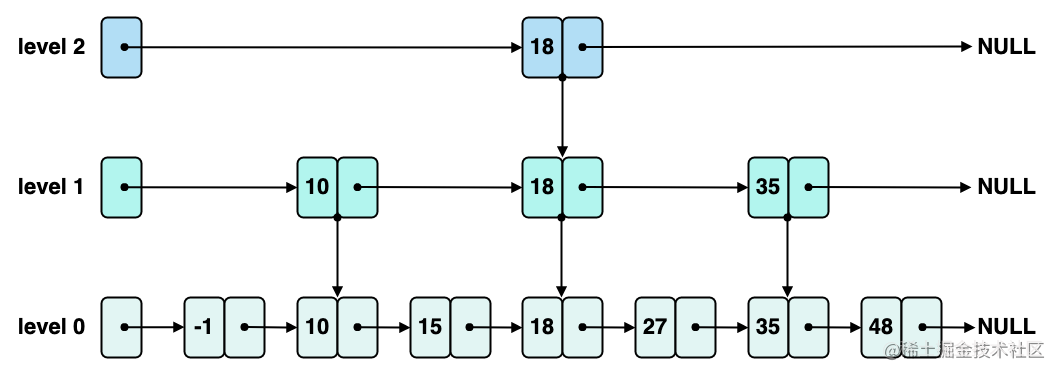
使用 skiplist 查找数据的时候，会先从最高层，也就是上图中的 level 2，开始向后遍历，这里发现 level 2 层小于 48 的最大节点是 18 节点，那么向下一层来到 level 1，继续从 18 节点向后遍历。在 level 1 层中发现小于 48 的最大节点是 35，那么再向下一层来到 level 0，继续从 35 节点向后迭代，最终找到 48 这个目标节点。

整个查找路径如下图红色箭头所示：

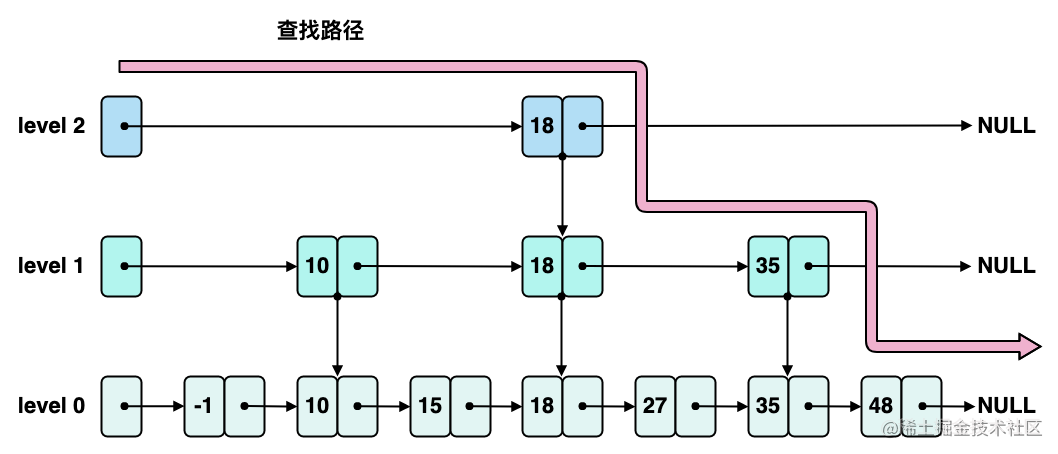
通过这个示例，我们可以体会到使用 skiplist 在结构上的特点：维护多层有序链表的索引，越往上层索引越稀疏，比如，level 2 就比 level 1 稀疏。在查找过程中，这些稀疏索引可以帮助我们跳过一些不必要的匹配操作。在利用 skiplist 这种稀疏索引进行查找的时候，我们需要使用到 cur 和 next 两个指针，当 next 节点的值比目标值大或是迭代到 NULL 时，则下降一层继续从 cur 开始向后遍历，直至找到目标节点或者返回 NULL。

zskiplist 核心实现

了解了 skiplist 的基本概念之后，我们再来深入分析一下 Redis 对 skiplist 的实现。其中，最核心、最基础的就是 zskiplistNode 结构体，其定义如下：

typedef struct zskiplistNode {

  sds ele; // 存储字符串类型的数据

  double score; // 用来排序的分数

  struct zskiplistNode *backward; // 指向当前层的前一个节点

  struct zskiplistLevel {

	struct zskiplistNode *forward; // 指向当前层的后一个节点

	unsigned long span; // 记录了当前层里面，我们按照forward指针向后走一步，

                            // 能扫过多少个元素

  } level[]; // skiplist中的层节点

} zskiplistNode;

zskiplistNode 中的 ele、score 字段都比较好理解，存的分别是元素值和分数值，backward 这个指针说明 Redis 的 skiplist 实现在 level 0 层实际是个双向链表。除此之外，zskiplistNode 还内嵌了一个 zskiplistLevel 结构体（即 level 柔性数组）来抽象层 skiplist 的层级，level 数组的下标索引标识了当前是第几层的 zskiplistNode 节点。

下图展示了单个 zskiplistNode 的结构示意图：

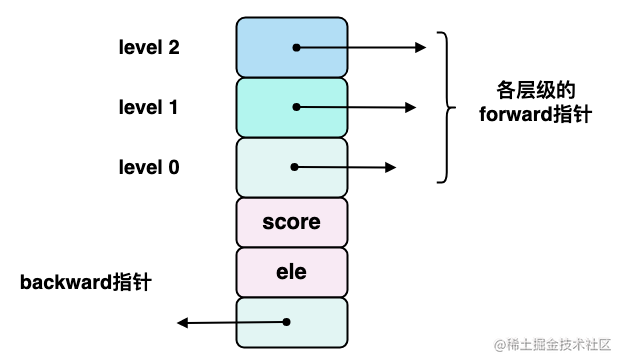
分析完 Redis 对单个 skiplist 节点的定义之后，我们再来看整个 skiplist 的实现，Redis 定义了一个 zskiplist 结构体来抽象 skiplist 这一数据结构，其具体定义如下：

typedef struct zskiplist {

  struct zskiplistNode *header, *tail; // 指向skiplist结构的首节点和尾结点

  unsigned long length; // 当前zskiplist level0的节点个数，也是其中存储元素的个数

  int level; // 当前zskiplist的层级数

} zskiplist;

zskiplist 核心函数

了解了 Redis 对 skiplist 这一数据结构的抽象之后，下面就要来关注怎么操作 skiplist 了。

创建 zskiplist

首先来看 Redis 是如何创建一个 zskiplist 实例的。我们来看 t_zset.c 文件中的 zslCreate() 函数，其核心逻辑是初始化 zskiplist 实例以及一个空的头节点，具体实现如下：

zskiplist *zslCreate(void) {

    int j;

    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl)); // 申请内存空间

    zsl->level = 1; // level设置为1

    zsl->length = 0; // zskiplist长度为0

    // 创建空的头节点，其中的score设置为0，ele设置为null

    // 其中的将level数组设置成ZSKIPLIST_MAXLEVEL值，默认值为32

    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);

    // 初始化header节点的各个level

    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {

        zsl->header->level[j].forward = NULL;

        zsl->header->level[j].span = 0;

    }

    // 初始化header节点的backward指针

    zsl->header->backward = NULL;

    zsl->tail = NULL; // 初始化zskiplist的尾指针

    return zsl;

}

这里需要展开介绍的是 zslCreateNode() 函数，其核心逻辑是为 zskiplistNode 节点申请空间，如下所示：

zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));

这里的关键点在于：不仅要为了 zskiplistNode 结构体申请空间，因为里面的 level 字段是个柔性数组，还需要为每个 level 层对应的 zskiplistLevel 申请空间，默认 header 节点的 level 是 32 层。

插入数据

创建完 zskiplist 实例之后，我们就可以开始关注于如何向这个 zskiplist 实例里面插入数据了，插入操作的入口是 zslInsert() 函数。先来看该函数依赖的两个辅助数组。

• update[] 数组：其中每个元素都是 zskiplistNode * 指针类型，记录了此次插入节点前面的一个节点，每层一个节点，所以是数组类型。举个例子，在下图这个 zskiplist 里面添加 50 这个元素，50 在各个层级的位置是图中粉红色节点的位置，在插入50 的时候，需要 update[] 数组辅助记录 50 前面的节点，比如图中的，update[0] 记录的就是插入节点在 level[0] 层中的前一个节点，也就是 48 这个节点。

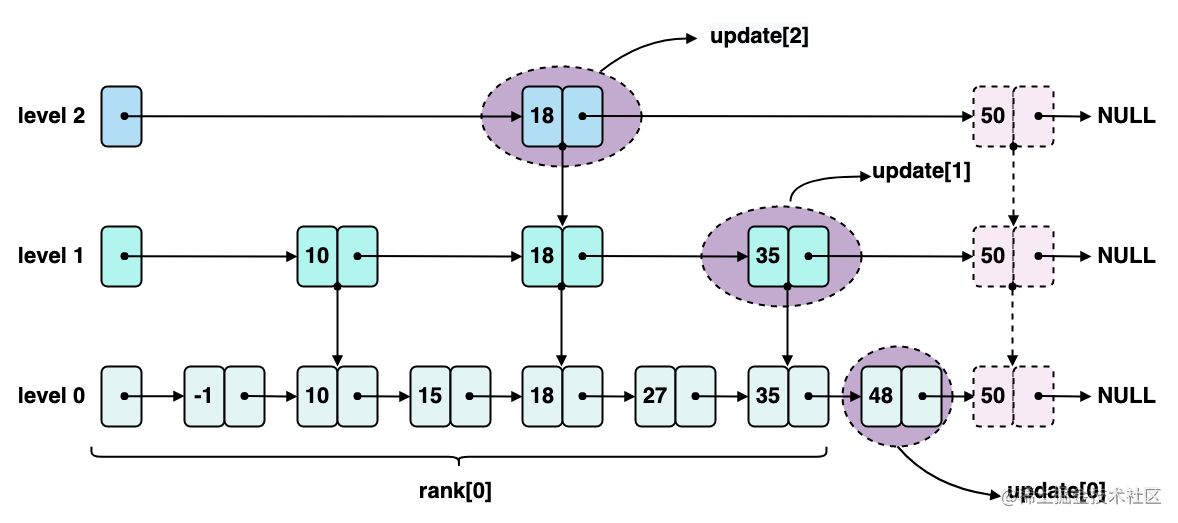
• rank[] 数组：记录每层从 header 节点遍历到 update[i] 节点所经过的节点个数，也就是 update[i] 节点是 zskiplist 中的第几个节点。这主要是为了设置新插入节点的 span 字段。如上图所示，rank[0] 记录了插入节点从 header 节点开始到插入节点需要经过的节点数。你可以结合 ZRANK 命令的功能，来理解 rank 数组的含义。

1. 查找插入位置

了解了辅助数组的具体含义之后，我们正式开始分析 zslInsert() 函数的逻辑，正如前文提到的 zskiplist 是一个有序链表，所以需要先根据插入值找到合适的插入位置，具体的实现如下：

zskiplistNode * x = zsl->header;

for (i = zsl->level-1; i >= 0; i--) { // 从顶层的header节点开始遍历

    // 如果是顶层的话，对应的rank[i]值初始化为0，如果是迭代过程中从i+1下降到

    // 了i层，会在前一层，也是就是rank[i+1]的基础上继续累加

    rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];

    // 下面开始在i这一层进行迭代

    while (x->level[i].forward && // 条件1：i这一层还有后续可迭代的节点

            (x->level[i].forward->score < score || // 条件2：后一个节点的score小于目标score

                // 条件3：如果score相等，需要后一个节点的ele小于目标ele

                (x->level[i].forward->score == score &&

                sdscmp(x->level[i].forward->ele,ele) < 0)))

    { // 满足上述三个条件，才能继续在i层向后

        rank[i] += x->level[i].span; // 递增rank[i]，记录这两个节点i这一层

        x = x->level[i].forward; // x指针后移

    }

    // 不满足上述三个条件的话，会降级到i-1层，降级之前需要将x节点记录

    // 到update[i]中，表示插入的新节点将在i层中的x节点之后

    update[i] = x;

}

下面我们通过一个示例来详细说明上述这段代码的核心逻辑。

假设现在要向下图展示的 zskiplist 中插入 score 为 40 的节点，初始化状态如下图所示，x 指向了 zskiplist 的 header 节点，此时 rank[2] 初始化为 0：

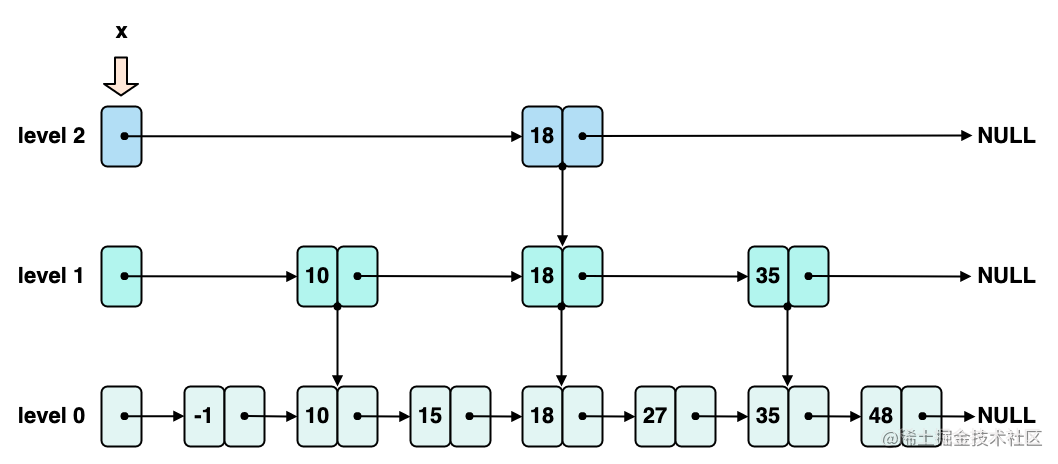
• level 2 层迭代过程

开始从 zskiplist 的最高层，也就是示例中的 level 2，向后遍历，此时如下图所示，x 指向 18 这个节点，x->level[2].forward 指向 NULL，同时会更新 rank[2] 为 4。

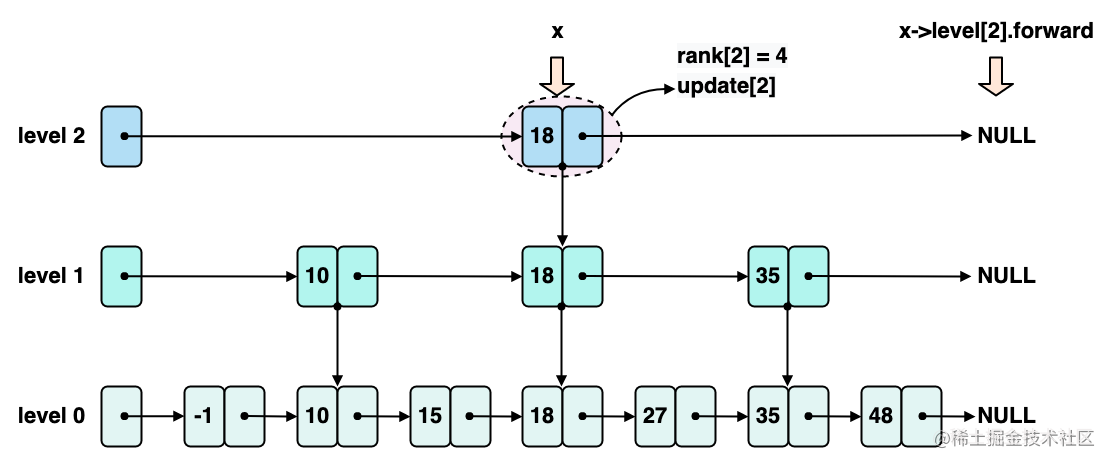
由于 x->level[2].forward 为 NULL，不满足条件 1，所以无法在 level 2 这一层上继续遍历了，需要更新 update[2] 指向节点 18。

• level 1 层迭代过程

接下来，进入 level 1 的迭代，x 依旧指向节点 18，但是关注的是 level 1 层的内容了，x->level[1].forward 指向节点 35，如下图所示，此时初始化 rank[1] 为 4。

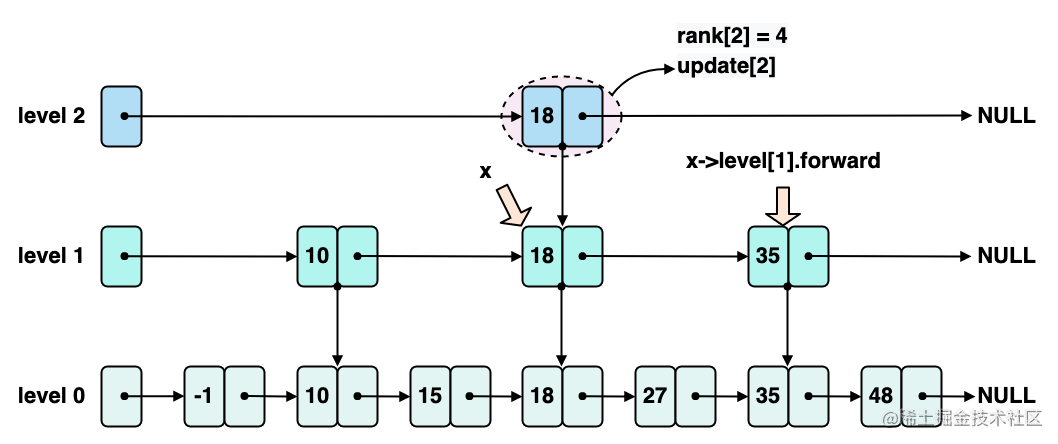
继续 level 1 的迭代，x 指向节点 35，x->level[1].forward 指向 NULL，同时更新 rank[1] 为 6，如下图所示：

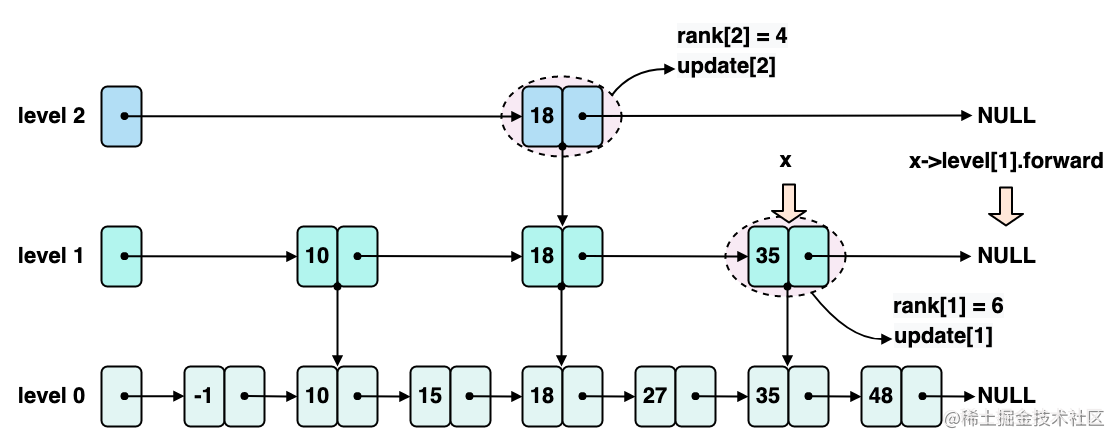
此时，因为 x->level[1].forward 为 NULL，不满足条件 1，所以已经无法在 level 1 继续迭代了，需要更新 update[1] 指向节点 35。

• level 0 迭代过程

最后，进入 level 0 的迭代，x 依旧指向节点 35，x->forward 指向节点 48，如下图所示，此时初始化 rank[0] 为 6。

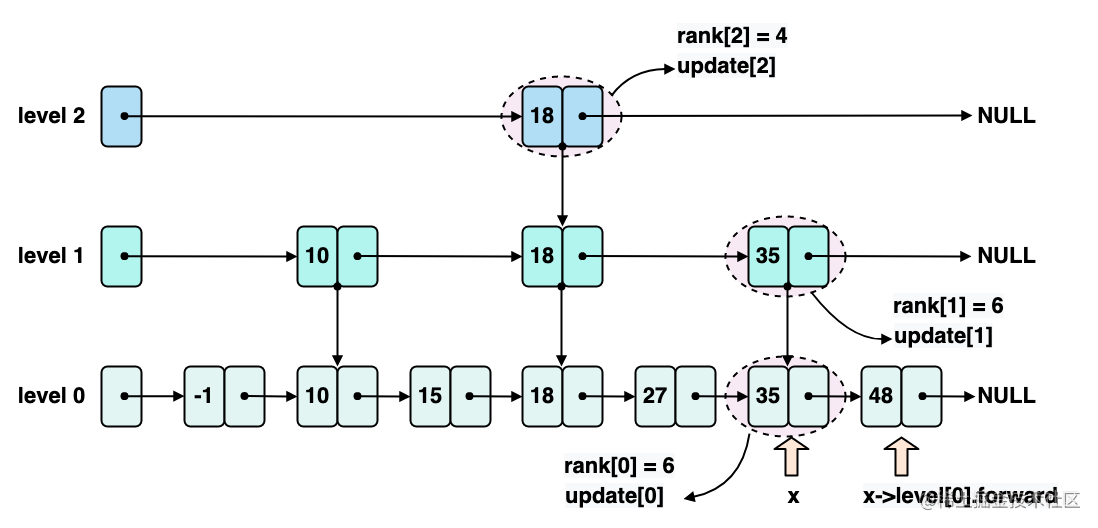
此时，因为 x->level[0].forward-score > 40，不满足条件 2，所以已经无法在 level 0 继续迭代了，需要更新 update[0] 指向节点 35。

到此为止，我们也就明确了新插入 score 为 40 的节点位于 35 和 48 两个节点之间。

2. 计算新节点的 level

确认了插入位置之后，接下来要做的就是计算新节点的 level 值，具体代码实现如下：

level = zslRandomLevel(); // 随机生成一个level值

if (level > zsl->level) {

    // 如果新生成的level值大于了zskiplist当前的level值时，则

    // 需要整个zskiplist的level升高

    for (i = zsl->level; i < level; i++) {

        rank[i] = 0; // 初始化新level对应的rank以及update数组

        // 新level一个节点都没有，插入位置是在header节点之后

        update[i] = zsl->header; 

        // 暂时初始化header节点的span字段，后面会在插入时重新根据rank计算并修改

        update[i]->level[i].span = zsl->length; 

    }

    zsl->level = level; // 升高整个zskiplist的level字段

}

升高 level 以及更新 rank 数组和 update 数组的一系列逻辑，都比较常规，但是有的同学可能会对 zslRandomLevel() 随机生成 level 值的行为感到担忧，一旦在一个只有几个元素的小 zskiplist 中，生成一个较大的 level 会造成资源浪费。那我们就再深入到 zslRandomLevel() 函数中看一下其具体实现：

int zslRandomLevel(void) {

    int level = 1;

    // ZSKIPLIST_P默认值为0.25

    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))

        level += 1;

    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;

}

这里关注其中的 while 循环条件，ZSKIPLIST_P 默认值为 0.25，也就是说每增高一层的概率为 25%，增高到 4 层的概率不到 0.4%，增高到 5 层的概率不到 0.01%，所以无需过度担心层高过高的问题。

3. 插入节点

计算完插入节点的 level 层级之后，我们就要开始插入新节点了，具体的代码片段如下：

// 创建新zskiplistNode节点，其中会初始化score、ele以及level数组

x = zslCreateNode(level,score,ele);

// 下面在各level中插入新节点，插入位置就是在对应的update[i]之后

for (i = 0; i < level; i++) {

    // 设置x节点的在各个层的forward指针

    x->level[i].forward = update[i]->level[i].forward;

    // 设置各层update节点的forward指针

    update[i]->level[i].forward = x;

    // 更新新插入节点以及前一个节点的span

    x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

    update[i]->level[i].span = (rank[0] - rank[i]) + 1;

}

下面我们依旧以插入 score 为 40 节点为示例，分析插入新节点这段逻辑，这里假设 40 这个节点随机生成的 level 为 2。在插入 level 0 时的指针操作，如下图所示：

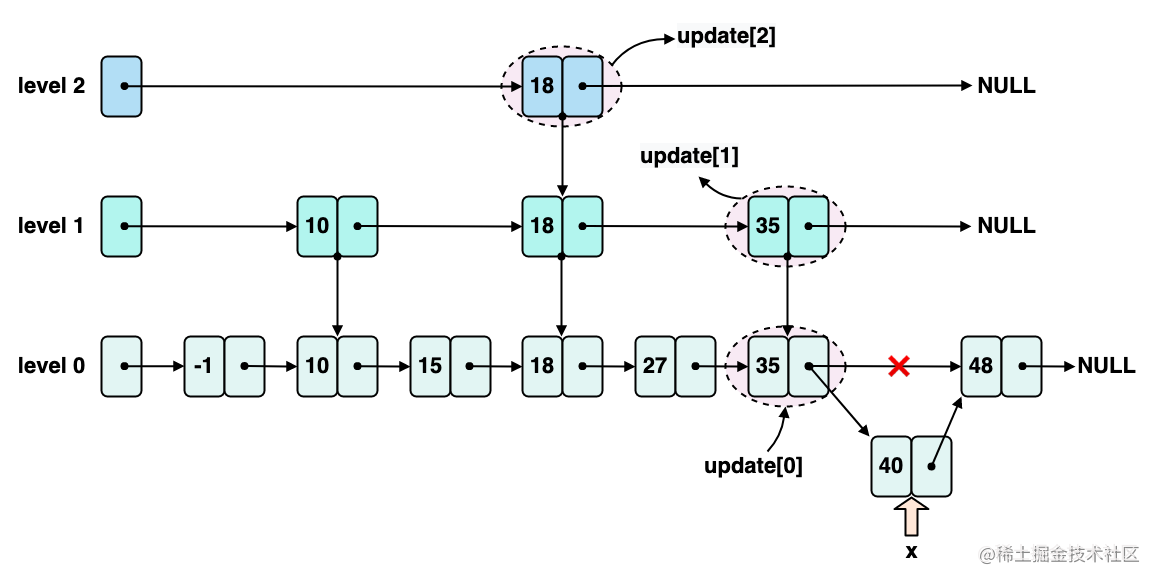
这里特别关注一下 span 字段的更新，我们知道 span 字段表示的是当前节点通过 forward 指针往后到下一个节点，扫过的元素个数。所以，新节点 x 插入的时候，不仅要设置新节点 x 的 span 值，还要更新 update[0] 节点的 span 值。在 level 0 中 update[0] 节点，也就是 35 节点，在新节点 x 插入之前，通过 forward 向后走一步，只扫过了 48 这个节点，所以 span 是 1；插入之后，通过 forward 向后走一步，只扫过 40 这个节点，所以 span 还是 1。同理，新节点 x，也就是 40 这个节点，在 level 0 中的 span 也是 1。

接下来看 level 1 这一层中 40 这个新节点的插入逻辑，主要还是 forward 指针的操作，如下图所示：

这里我们还是来关注一下，新节点 x 在 level 1 层插入时导致的 span 更新：在 level 1 中，update[0] 节点，也就是 35 节点，在新节点 x 插入之前，通过 forward 向后走一步，到了 NULL，但是还是可以扫过且只扫过 48 这个节点的，所以 span 是 1；插入之后，通过 forward 向后走一步，扫过且只扫过 40 这个节点，所以 span 还是 1。新节点 x 插入之后，在 level 1 中，通过 forward 指针向后走一步，得到 NULL，但扫过且只扫过 48，所以 span 也是 1。

我们抽象一下上述逻辑，转换成统一的 span 更新逻辑，rank[i] 记录了 update[i] 是第几个节点，rank[0] - rank[i] 得到的就是 update[i] 到 x 节点的节点数，如下图所示：

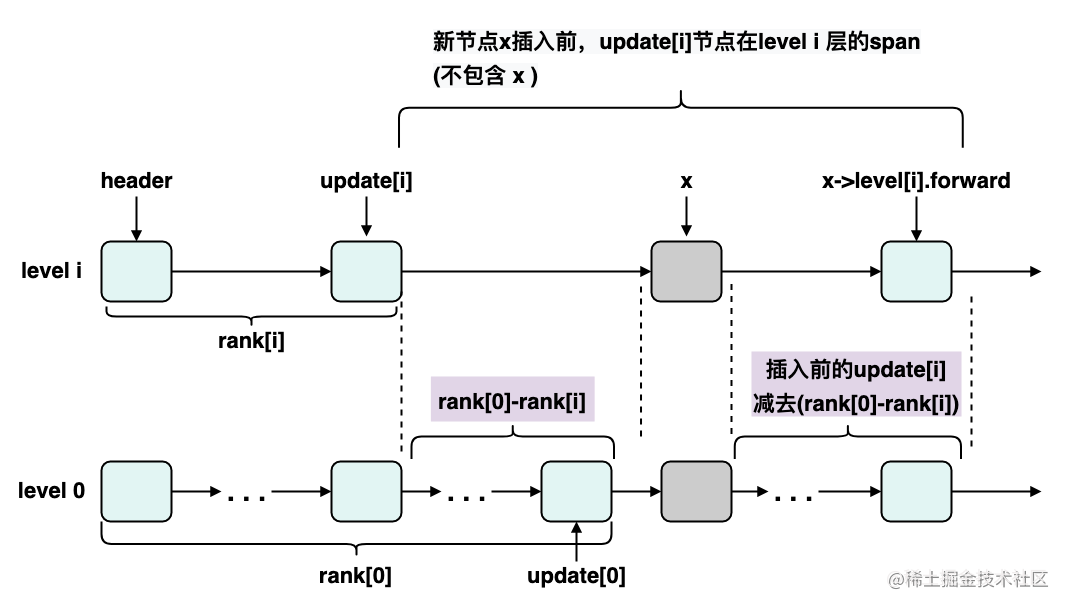
那么从上图可以直接看出，在 level i 层中，x->level[i].span 是插入前 updater[i]->level[i].span 减去（rank[0] - rank[1]），插入后的 update[i]->level[i].span 是 rank[0] - rank[i] +1。

到这里，插入操作还没全部完成，当前 zskiplist 总共三层，虽然新节点 x 只有两层，zskiplist 的 level 2 中不需要有指针操作，但是 x 节点是插入到了 update[2] 节点之后，会影响到其 span 值，所以还需要执行下面这个循环，更新 update[2] 节点在 level 2 中的 span 值：

for (i = level; i < zsl->level; i++) {

    // 无指针操作的level中，对应的update[i]节点的span会受影响

    update[i]->level[i].span++;

}

4. 修改 backward 指针

到此为止，我们已经完成了新节点的插入，在 zslInsert() 函数的最后，会调整 level 0 中新节点以及其后节点的 backward 指针，相关代码实现如下：

// 调整新插入节点的backward指针，x为第一个节点的话，其backward会指向NULL，

// 否则，指向update[0]节点即可

x->backward = (update[0] == zsl->header) ? NULL : update[0];

if (x->level[0].forward) // 调整x之后节点的backward指针

    x->level[0].forward->backward = x;

else // 如果x是最后一个节点，zskiplist的尾指针会指向x

    zsl->tail = x;

zsl->length++; // 最后，增加zskiplist长度并返回x这个新插入的节点

return x;

删除数据

了解了 zskiplist 的插入逻辑之后，我们再来看一下从 zskiplist 中删除节点的实现。从 zskiplist 中删除数据的入口是 zslDelete() 函数，其核心逻辑如下。

1. 首先，根据传入的 score 分数值以及 ele 值，查找要删除的目标节点。该查找过程与 zslInsert() 函数中查找插入位置的逻辑基本类似，这里不再重复。

2. 在查找到待删除的目标节点之后，会调用 zslDeleteNode() 函数进行删除。

3. 目标节点从 zskiplist 中删除之后，会根据 zslDelete() 函数的 node 参数（第三个参数）决定是将 node 指针指向这个删除的目标节点，作为输出参数传给调用方，还是调用 zslFreeNode() 函数销毁掉节点。在zslFreeNode() 函数中会先销毁节点中 ele 字段记录的 sds 实例，然后销毁节点对应的 zskiplistNode 实例。

这里我们展开介绍一下 zslDeleteNode() 函数的逻辑。

1. 删除目标节点的时候，必然会影响前一个节点的 span 值，所以首先要执行下面这个 for 循环，逐层调整前一个节点的 span 值，具体代码实现如下：

int i;

for (i = 0; i < zsl->level; i++) { // 逐层调整对应的update[i]

    if (update[i]->level[i].forward == x) {

        // 待删除的x节点如果在i层中，则需要修改update[i]节点的span，

        // 将其合并x节点的span，这里之所以减 1，是因为要删除x节点

        update[i]->level[i].span += x->level[i].span - 1;

        // 修改update[i]的forward指针

        update[i]->level[i].forward = x->level[i].forward;

    } else {

        // 如果待删除的x节点没有在i层中，只需要将update[i]节点的span减1即可

        update[i]->level[i].span -= 1;

    }

}

2. 接下来，调整 level 0 层的 backward 指针，具体实现如下：

if (x->level[0].forward) {

    // x节点后面的节点存在，则将其backward指针指向x节点的前一个节点

    x->level[0].forward->backward = x->backward;

} else {

    // 如果x是最后一个节点，在x删除之后，zskiplist尾指针要指向x前面的节点

    zsl->tail = x->backward;

}

3. 最后，如果删除的 x 节点是最高 level 中的唯一节点，那整个 zskiplist 的 level 将会降低，同时还会调整整个 zskiplist 的长度，具体实现如下：

// 如果删除的x节点是最高level中的唯一节点，那整个zskiplist的level将会降低

while(zsl->level > 1 && 

      zsl->header->level[zsl->level-1].forward == NULL)

    zsl->level--;

zsl->length--; // 更新zskiplist的长度

总结

本节我们详细介绍了 Redis 中 skiplist 相关的内容。

• 首先，阐明了 skiplist 这个数据结构的基本概念和其高效查询的原理。
• 然后，深入分析了 Redis 对 skiplist 的抽象，其中涉及 zskiplistNode、zskiplist 等核心结构体的解析。
  的 x 节点是最高 level 中的唯一节点，那整个 zskiplist 的 level 将会降低，同时还会调整整个 zskiplist 的长度，具体实现如下：

// 如果删除的x节点是最高level中的唯一节点，那整个zskiplist的level将会降低

while(zsl->level > 1 && 

      zsl->header->level[zsl->level-1].forward == NULL)

    zsl->level--;

zsl->length--; // 更新zskiplist的长度

总结

本节我们详细介绍了 Redis 中 skiplist 相关的内容。

• 首先，阐明了 skiplist 这个数据结构的基本概念和其高效查询的原理。
• 然后，深入分析了 Redis 对 skiplist 的抽象，其中涉及 zskiplistNode、zskiplist 等核心结构体的解析。
• 最后，拆解了 Redis 中操作 zskiplist 的核心函数，例如，创建 zskiplist 和 zskiplistNode 实例函数、向 zskiplist 插入新节点的核心流程，以及从 zskiplist 中删除节点的流程。

🔥运维干货分享

• 软考高级系统架构设计师备考学习资料
• 软考中级数据库系统工程师学习资料
• 软考高级网络规划设计师备考学习资料
• 软考高级系统规划与管理师学习资料
• 软考中级系统集成项目管理师学习资料
• Kubernetes CKA认证学习资料分享
• AI大模型学习资料合集
• PuTTY中文版安装包
• MobaXterm中文版安装包
• pinginfoview网络诊断工具中文版
• Xshell、Xsftp、Xmanager中文版安装包
• 毕业设计高质量毕业答辩 PPT 模板分享
• IT行业工程师面试简历模板分享