数据结构与算法（5）---二叉树

杭州杭州杭州2026-01-19 11:43

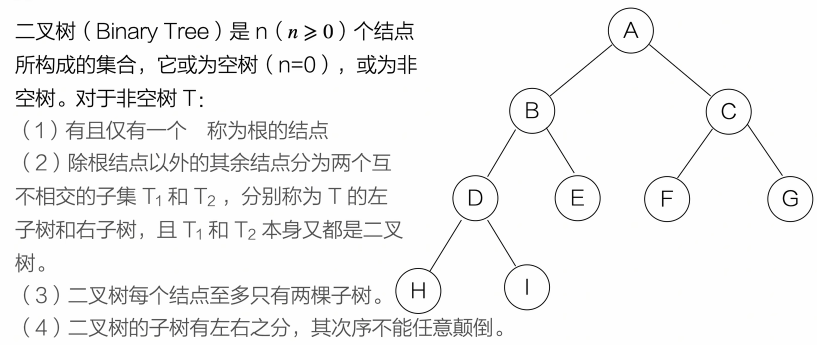
二叉树与遍历

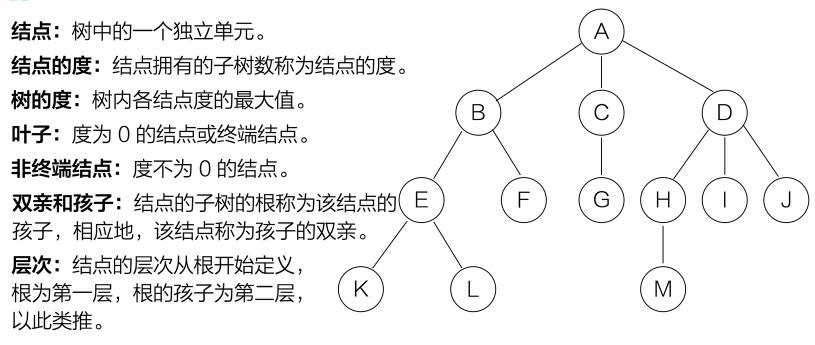
基本概念和性质

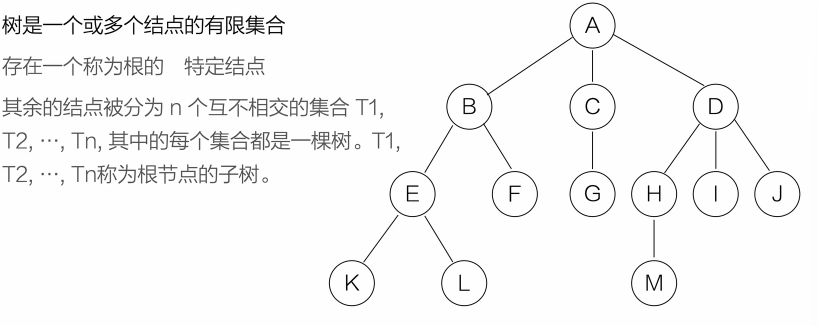
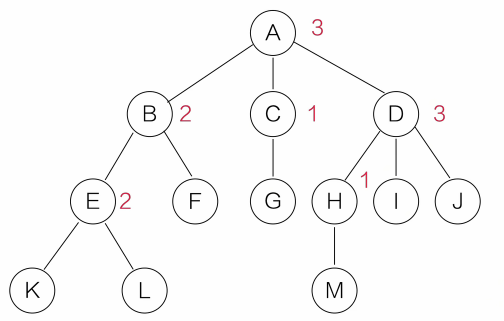
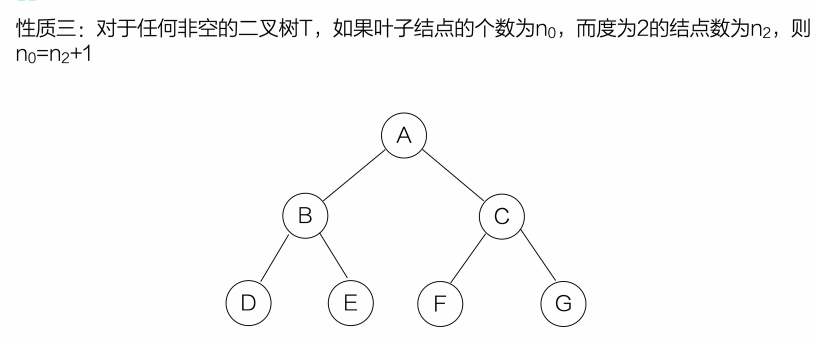
性质一：树中所有结点数等于所有结点度数之和加1

性质二：对于度为m的树，第i层上最多有 m\^{i-1} 个结点

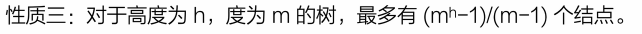
二叉树

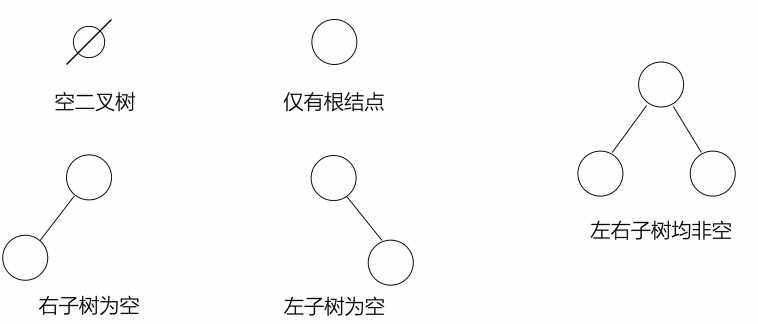
二叉树基本形态

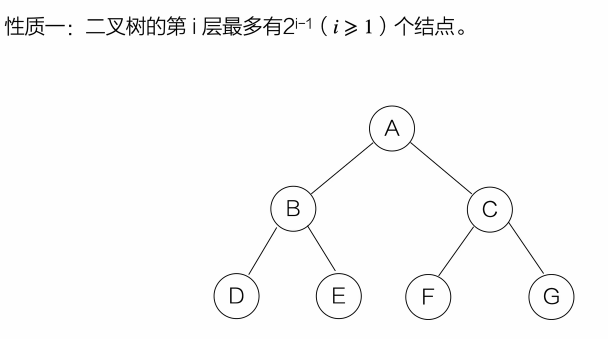
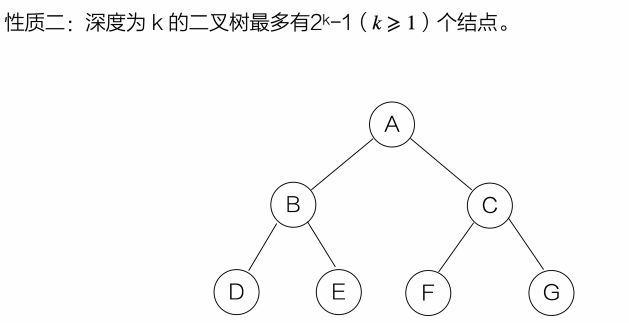
  1. 二叉树的性质
  1. 特殊二叉树
    （1） 满二叉树
复制代码 
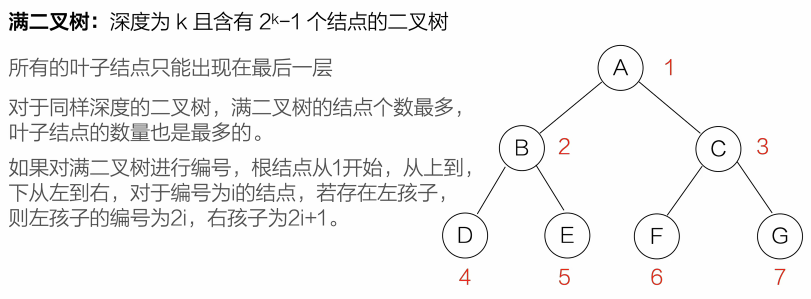
 （2）完全二叉树

层层满，最后一层靠左站

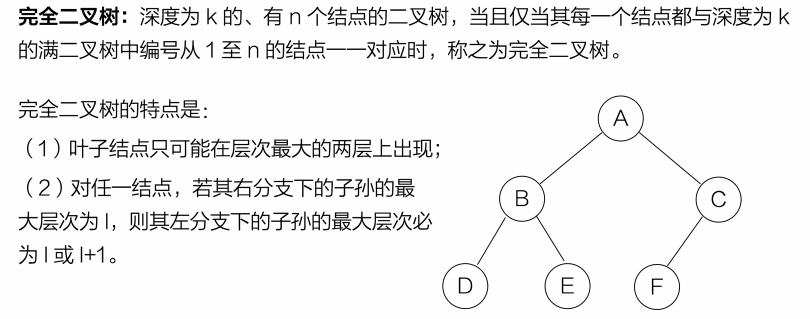
完全二叉树特别适合用数组存储（比如堆 heap）：

如果从 1 开始编号：

  • 父结点 i
  • 左孩子：2i
  • 右孩子：2i + 1

（从 0 开始编号则是：左 2i+1，右 2i+2）

性质：

复制代码 
（3）做个题目：

选D

  • 前5层能有多少结点？
    • 1+2+4+8+16=311+2+4+8+16=311+2+4+8+16=31
  • 第6层最多能放多少结点？
    • 二叉树每层最多翻倍，所以第6层最多： 2\^5 =32
  • 题目说第6层有8个叶子
    • 第6层有 8 个结点是叶子 = 它们没有孩子假如第6层一共放了32个结点，其中 8个是叶子（没孩子），剩下的 32-8=24个不是叶子（有孩子），所以第6层"能继续往下长"的结点数 = 24个
  • 这些"不是叶子"的结点能长出第7层多少结点？
    • 每个"不是叶子"的结点，都必须有2个孩子（因为完全二叉树中，内部结点一定有两个孩子），所以第7层能长出：24×2=48个结点

总数：

31+32+48=11131+32+48=11131+32+48=111

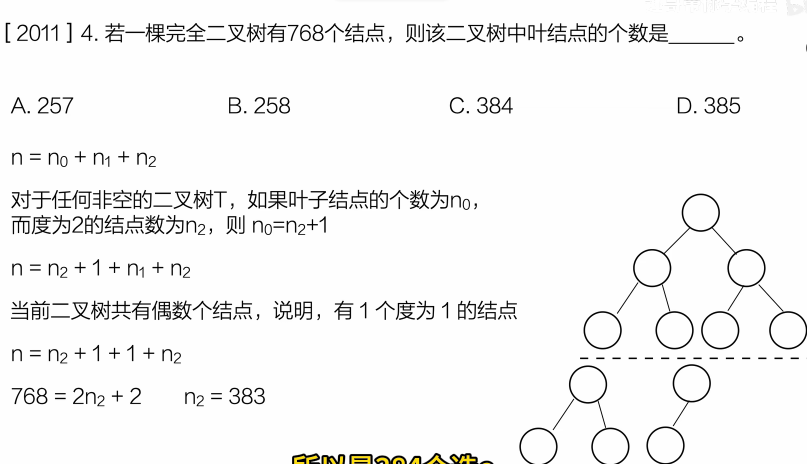
选C

  1. 二叉树的存储结构

顺序存储结构

除了满二叉树和完全二叉树外，其他场景比较浪费空间

链式存储结构

c 复制代码 
typedef char ElemType;
typedef struct TreeNode
{
    ElemType data;
    TreeNode *lchild;
    TreeNode *rchild;
}TreeNode;
// Bi是单词binary（二进制）
//给 TreeNode*（指向 TreeNode 结点的指针类型）起一个别名叫 BiTree
typedef TreeNode* BiTree;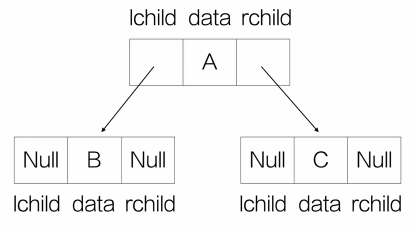

二叉树的遍历

拿这个举例：

c 复制代码 
      A
     / \
    B   C
   / \
  D   E
  1. 前序遍历（根左右）
c 复制代码 
void preOrder(BiTree T){
    if(T==NULL){
        return;
    }
    printf("%c",T->data);
    preOrder(T->lchild);
    preOrder(T->rchild);
}

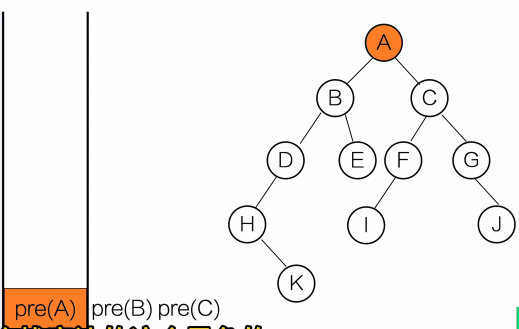
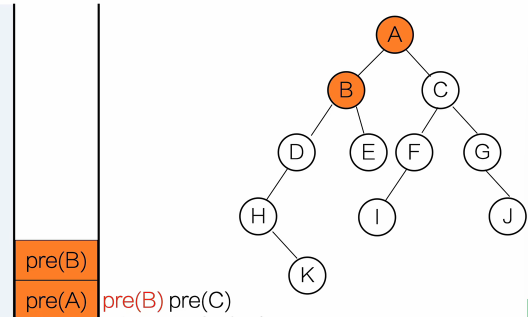
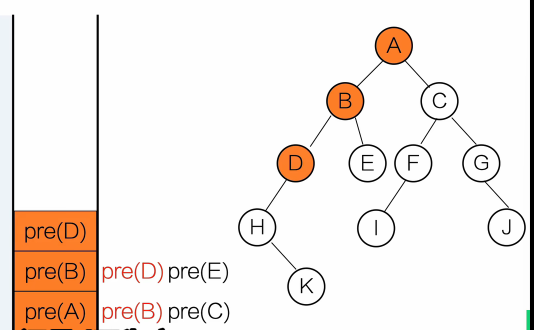
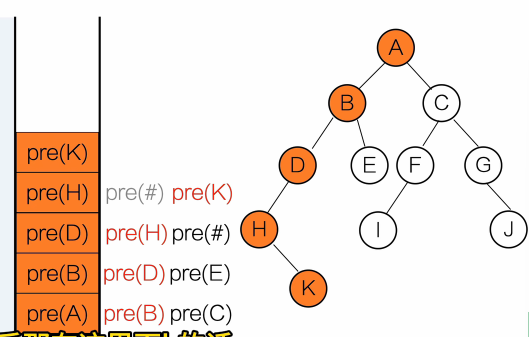
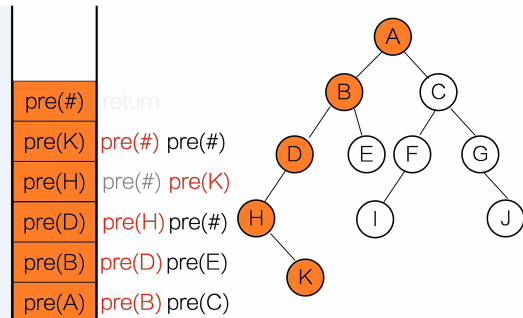
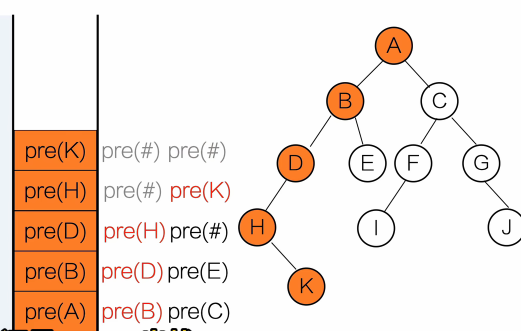
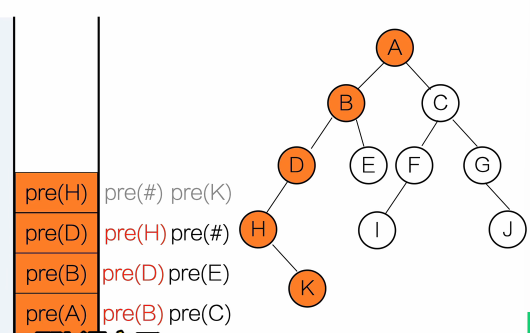
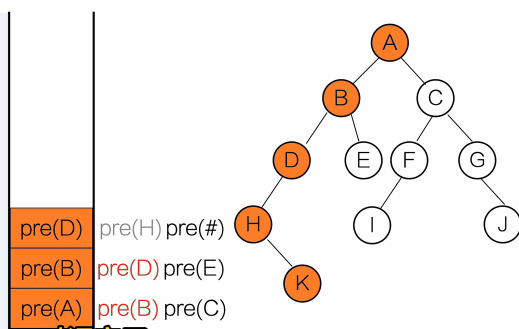
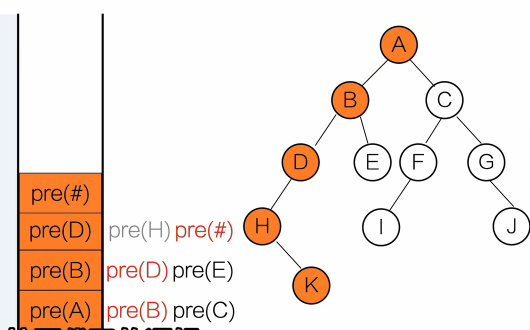
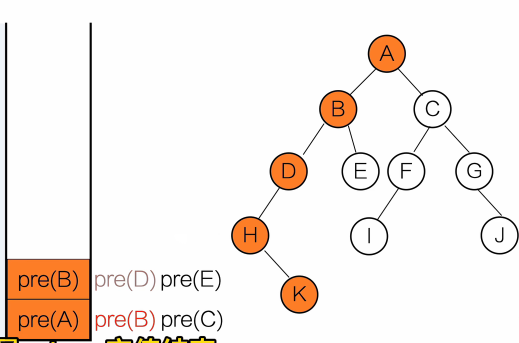
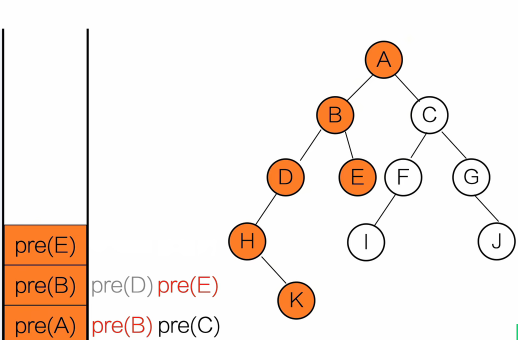
输出顺序：A B D E C

用栈去理解

黑色：等待调用

红色：正在调用

灰色：调用完成

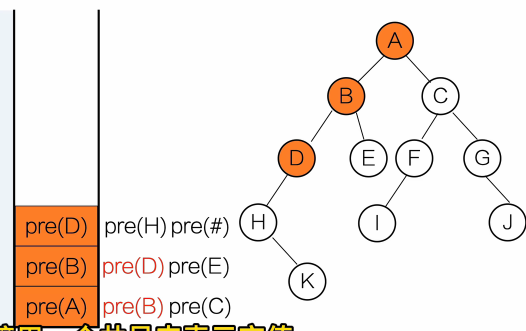
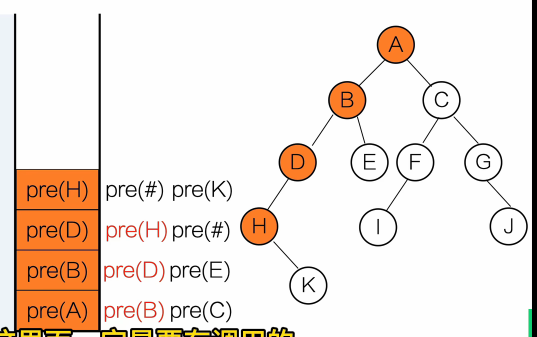
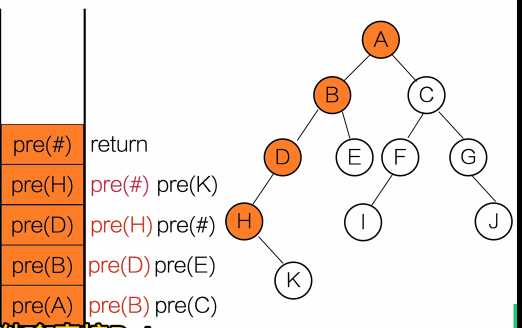
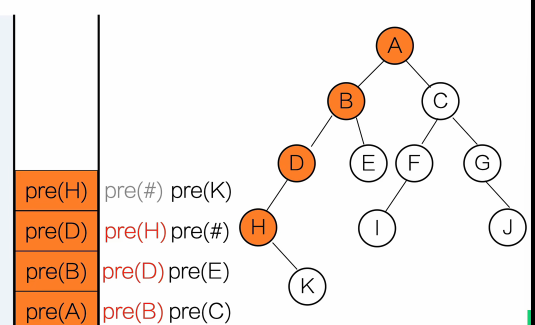
  1. 中序遍历（左根右）

先访问根结点，向树的左下方移动，直到遇到空结点为止，然后访问空结点的父结点。接着继续遍历该结点的右子树，如果右子树没的子树可以遍历，那么继续遍历上一层最后一个未被访问的结点

c 复制代码 
void inOrder(BiTree T){
    if(T==NULL) return;
    inOrder(T->lchild);
    printf("%c",T->data);
    inOrder(T->rchild);
}

输出顺序：D B E A C

  1. 后序遍历（左右根）

从根结点开始先访问结点的左右儿子，再对该结点进行访问。这就意味着结点的儿子将再该结点之前输出

c 复制代码 
void postOrder(BiTree T){
    if(T==NULL) return;
    postOrder(T->lchild);
    postOrder(T->rchild);
    printf("%c",T->data);
}

输出顺序：D E B C A

举个例子：

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef char ElemType;
typedef struct TreeNode
{
    ElemType data;
    TreeNode *lchild;
    TreeNode *rchild;
}TreeNode;

typedef TreeNode* BiTree;

// 空结点用#
char str[]="ABDH#K###E##CFI###G#J##";
//         A
//       /   \
//      B     C
//    /  \   / \
//   D    E F   G
//  /      /     \
// H      I       J
//  \
//   K

int idx=0;

void createTree(BiTree *T){
    ElemType ch;
    ch=str[idx++];
    if(ch=='#'){
        *T=NULL;
    }else{
        // 1) 先创建当前结点
        *T = (BiTree)malloc(sizeof(TreeNode));
        (*T)->data = ch;

        // 2) 递归创建左子树
        createTree(&((*T)->lchild));

        // 3) 递归创建右子树
        createTree(&((*T)->rchild));
    }
}

//前序遍历
void preOrder(BiTree T){
    if(T==NULL){
        return;
    }
    printf("%c",T->data);
    preOrder(T->lchild);
    preOrder(T->rchild);
}



//中序遍历
void inOrder(BiTree T){
    if(T==NULL){
        return;
    }
    inOrder(T->lchild);
    printf("%c",T->data);
    inOrder(T->rchild);
}


//后序遍历
void postOrder(BiTree T){
    if(T==NULL){
        return;
    }
    postOrder(T->lchild);
    postOrder(T->rchild);
    printf("%c",T->data);
}



int main(){
    BiTree T;
    createTree(&T);
    preOrder(T);   // ABDHKECFIGJ
    printf("\n");
    inOrder(T);   // HKDBEAIFCGJ
    printf("\n");
    postOrder(T); // KHDEBIFJGCA
    printf("\n");
}
  1. 非递归前序遍历

用循环 + 栈 来完成二叉树的前序遍历（根→左→右），而不是用函数自己调用自己（递归）

c 复制代码 
/* 非递归前序：根-左-右 */
void iterPreOrder(Stack *s, BiTree T) {
    while (T != NULL || !isEmpty(s)) {
        while (T != NULL) {
            printf("%c ", T->data);  // 访问根
            push(s, T);              // 根入栈，等会儿回来走右子树
            T = T->lchild;           // 一路向左
        }
        pop(s, &T);                  // 回退到最近祖先
        T = T->rchild;               // 转向右子树
    }
}
  1. 根据遍历结果推导二叉树

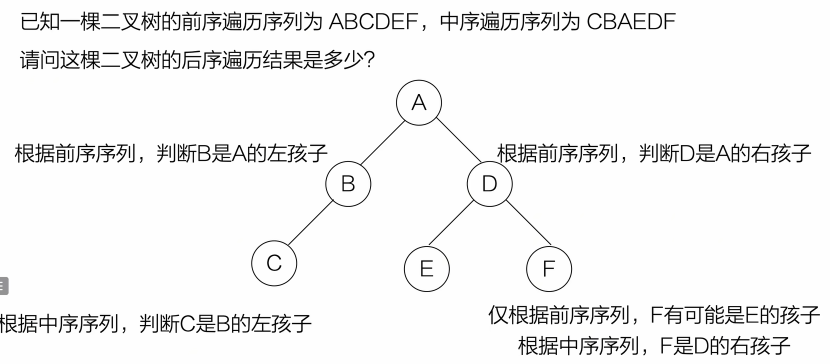
已知前序遍历和中序遍历，可以唯一确定一棵二叉树

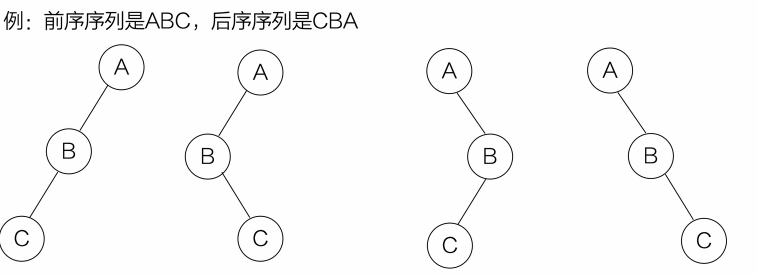
已知中序遍历和后序遍历，可以唯一确定一棵二叉树

已知前序遍历和后序遍历，是不能确定一棵二叉树的

线索二叉树

  1. 基本定义

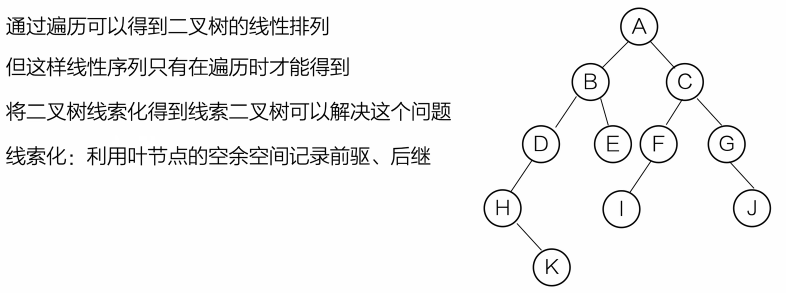
线索二叉树通过利用空指针保存遍历序列中的前驱和后继信息，使遍历过程无需递归和栈，并能快速找到结点的前驱/后继，从而提高遍历效率

例如中序线索树：

  • 没有左孩子 ⇒ 左指针指向中序前驱
  • 没有右孩子 ⇒ 右指针指向中序后继

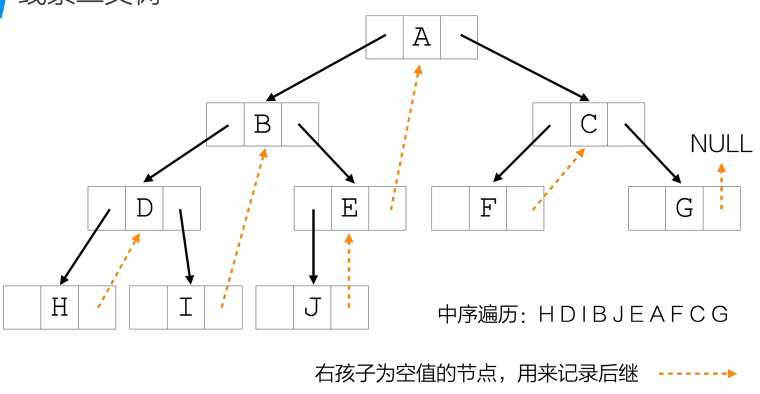
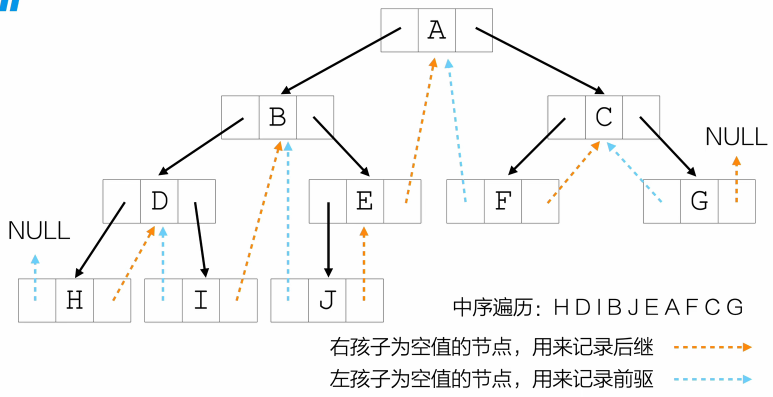
有n个结点----->有n+1个NULL

需要的改变：

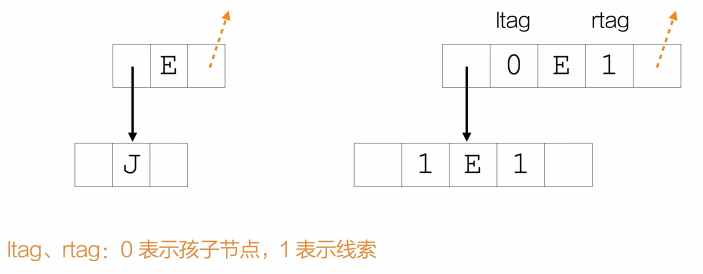
存储结构：

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef char ElemType;
typedef struct ThreadNode
{
    ElemType data;
    struct ThreadNode *lchild;
    struct ThreadNode *rchild;
    int ltag;
    int rtag;
}ThreadNode;

typedef ThreadNode* ThreadTree;

ltag为0时，指向该结点左孩子，为1时，指向该结点的前驱

rtag为0时，指向该结点右孩子，为1时，指向该结点的后继

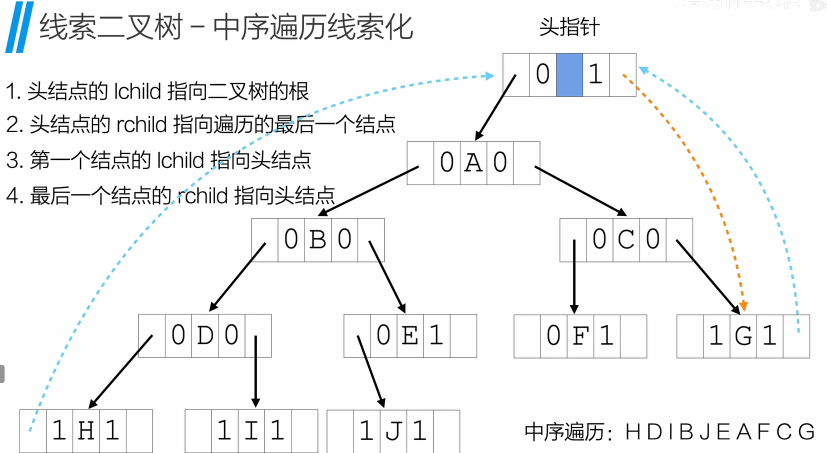
  1. 中序遍历线索化
  • 头结点的lchild指向二叉树的根
  • 头节点的rchild指向遍历的最后一个结点
  • 第一个结点的lchild指向头结点
  • 最后一个结点的rchild指向头结点
c 复制代码 
#include <stdio.h>
#include <stdlib.h>

typedef char ElemType;
typedef struct ThreadNode {
    ElemType data;
    struct ThreadNode *lchild;
    struct ThreadNode *rchild;
    int ltag;  // 0: 左孩子  1: 前驱线索
    int rtag;  // 0: 右孩子  1: 后继线索
} ThreadNode;

typedef ThreadNode* ThreadTree;

char str[] = "ABDH##I##EJ###CF##G##";
int idx = 0;

ThreadTree prev = NULL;

// 先序创建二叉树（# 表示空）
void createTree(ThreadTree *T) {
    ElemType ch = str[idx++];

    if (ch == '\0') {   // 防御：串结束
        *T = NULL;
        return;
    }

    if (ch == '#') {
        *T = NULL;
    } else {
        *T = (ThreadTree)malloc(sizeof(ThreadNode));
        if (!*T) {
            perror("malloc");
            exit(1);
        }

        // 必须初始化
        (*T)->data = ch;
        (*T)->lchild = NULL;
        (*T)->rchild = NULL;
        (*T)->ltag = 0;
        (*T)->rtag = 0;

        createTree(&((*T)->lchild));
        createTree(&((*T)->rchild));
    }
}

// 具体线索化（中序线索化核心）
void threading(ThreadTree T) {
    if (T != NULL) {
        // 左子树
        if (T->ltag == 0) threading(T->lchild);

        // 当前结点：处理前驱线索
        if (T->lchild == NULL) {
            T->ltag = 1; 
            T->lchild = prev;
        }

        // 处理 prev 的后继线索
        if (prev != NULL && prev->rchild == NULL) {
            prev->rtag = 1;
            prev->rchild = T;
        }

        prev = T;

        // 右子树
        if (T->rtag == 0) threading(T->rchild);
    }
}

// 开始线索化（带头结点）
void inOrderThreading(ThreadTree *head, ThreadTree T) {
    *head = (ThreadTree)malloc(sizeof(ThreadNode));
    if (!*head) {
        perror("malloc");
        exit(1);
    }

    (*head)->data = '\0';
    (*head)->ltag = 0;
    (*head)->rtag = 1;
    (*head)->rchild = *head;

    if (T == NULL) {
        (*head)->lchild = *head;
        return;
    }

    (*head)->lchild = T;
    prev = *head;

    threading(T);

    // 最后一个结点的后继线索指向 head
    prev->rtag = 1;
    prev->rchild = *head;

    // head 的右指针指向最后一个结点
    (*head)->rchild = prev;
}

// 使用线索进行中序遍历
void inOrder(ThreadTree head) {
    ThreadTree curr = head->lchild;

    while (curr != head) {
        while (curr->ltag == 0) curr = curr->lchild;

        printf("%c ", curr->data);

        while (curr->rtag == 1 && curr->rchild != head) {
            curr = curr->rchild;
            printf("%c ", curr->data);
        }

        curr = curr->rchild;
    }
    printf("\n");
}

int main() {
    ThreadTree T = NULL;
    ThreadTree head = NULL;

    idx = 0;
    createTree(&T);

    inOrderThreading(&head, T);

    inOrder(head);

    return 0;
}

inOrder(head)核心思路：

  1. 从根开始一路向左走到"最左"（ltag==0 才表示真左孩子）
  2. 访问这个结点
  3. 如果它 rtag==1，说明右指针是后继线索，就顺着线索一路访问下去
  4. 否则 rtag==0，右指针是真右子树，就跳到右子树，再重复步骤 1
相关推荐
万象.2 小时前
redis数据结构list的基本指令
数据结构·redis·list
zephyr052 小时前
C++ STL unordered_set 与 unordered_map 完全指南
开发语言·数据结构·c++
漫随流水2 小时前
leetcode算法（112.路径总和）
数据结构·算法·leetcode·二叉树
企鹅侠客3 小时前
第24章—数据结构篇：skiplist原理与实现解析
数据结构·skiplist
Chan163 小时前
【 微服务SpringCloud | 模块拆分 】
java·数据结构·spring boot·微服务·云原生·架构·intellij-idea
早川9193 小时前
9种常用排序算法总结
数据结构·算法·排序算法
卷毛迷你猪3 小时前
小肥柴慢慢手写数据结构（C篇）（2.1.1 动态数组（ArrayList））
c语言·数据结构
Yupureki4 小时前
《算法竞赛从入门到国奖》算法基础:入门篇-离散化
c语言·数据结构·c++·算法·visual studio
散峰而望4 小时前
OJ 题目的做题模式和相关报错情况
java·c语言·数据结构·c++·vscode·算法·visual studio code
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Linux下V2Ray安装配置指南05UV安装并设置国内源06Claude Code Skills 实用使用手册07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08Labelme从安装到标注：零基础完整指南09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10BongoCat - 跨平台键盘猫动画工具