目录
[1 U-Net 代码](#1 U-Net 代码)
[1.1 网络架构](#1.1 网络架构)
[1.2 数据增强](#1.2 数据增强)
[2 Sinkhorn 算法实操](#2 Sinkhorn 算法实操)
[2.1 手动计算迭代](#2.1 手动计算迭代)
[2.2 代码](#2.2 代码)
[3 总结](#3 总结)
摘要
本周首先利用代码梳理了 U-Net 的网络结构及弹性形变,了解了其实现细节与尺寸变换,同时认识了插值这一数据处理方法;其次,手动梳理了 Sinkhorn 算法的迭代过程,并利用代码对其进行了实现,同时了解了收敛容差这一参数的作用与选择策略。
Abstract
This week, I first used code to analyze the network structure and elastic deformation of U-Net, gaining an understanding of its implementation details and size transformations, while also learning about interpolation as a data processing method. Next, I manually examined the iterative process of the Sinkhorn algorithm and implemented it using code, while also studying the role of the convergence tolerance parameter and strategies for selecting it.
1 U-Net 代码
1.1 网络架构
从实现角度看,U-Net的代码结构清晰反映了其架构思想。
其输入层接收原始图像,经过一个初始双卷积块(两个 3x3 卷积+ReLU)提取基础特征;编码器部分由四个下采样阶段组成,每个阶段先进行 2x2 最大池化,然后将特征通道数加倍并应用双卷积块;编码器后接一个瓶颈层,采经过一个双卷积块,此时特征图尺寸最小但语义信息最丰富;解码器与编码器相对应,包含四个上采样阶段,每个阶段首先使用 2x2 转置卷积进行上采样,然后将结果与编码器对应层的特征图拼接;拼接后的特征图经过两个3x3卷积和ReLU进行融合;输出层使用 1x1 卷积将特征映射到类别空间。
由于输入层、编码器、瓶颈层与解码器都采用了双卷积块,故在代码中对其进行定义,以方便后续调用。其代码如下:
python
# 双卷积块
class DoubleConv(nn.Module):
def __init__(self, in_channels, out_channels):
super(DoubleConv, self).__init__() # 初始化
self.conv = nn.Sequential(
# 第一个3x3卷积(无填充,输出尺寸会缩小)
nn.Conv2d(in_channels, out_channels, kernel_size=3, padding=0),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True), # 直接修改输入张量,如果需在反向传播中使用原始输入则不能使用
# 第二个3x3卷积(无填充)
nn.Conv2d(out_channels, out_channels, kernel_size=3, padding=0),
nn.BatchNorm2d(out_channels),
nn.ReLU(inplace=True)
)
def forward(self, x):
return self.conv(x)整个网络包含23个卷积层,全部使用无填充卷积,输出尺寸比输入小一定的边框宽度。整体网络结构代码如下:
python
class UNetOriginal(nn.Module):
def __init__(self, in_channels=1, out_channels=2):
super(UNetOriginal, self).__init__()
# 编码器路径(下采样)
# 第一层
self.enc1 = DoubleConv(in_channels, 64)
self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
# 第二层
self.enc2 = DoubleConv(64, 128)
self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
# 第三层
self.enc3 = DoubleConv(128, 256)
self.pool3 = nn.MaxPool2d(kernel_size=2, stride=2)
# 第四层
self.enc4 = DoubleConv(256, 512)
self.pool4 = nn.MaxPool2d(kernel_size=2, stride=2)
# 瓶颈层
self.bottleneck = DoubleConv(512, 1024)
# 解码器(上采样)
# 上采样4层
self.upconv4 = nn.ConvTranspose2d(1024, 512, kernel_size=2, stride=2)
self.dec4 = DoubleConv(1024, 512) # 输入通道 512(上采样) + 512(跳跃连接)
# 上采样3层
self.upconv3 = nn.ConvTranspose2d(512, 256, kernel_size=2, stride=2)
self.dec3 = DoubleConv(512, 256)
# 上采样2层
self.upconv2 = nn.ConvTranspose2d(256, 128, kernel_size=2, stride=2)
self.dec2 = DoubleConv(256, 128)
# 上采样1层
self.upconv1 = nn.ConvTranspose2d(128, 64, kernel_size=2, stride=2)
self.dec1 = DoubleConv(128, 64)
# 输出层
self.out_conv = nn.Conv2d(64, out_channels, kernel_size=1)
def forward(self, x):
# 编码器路径
# 第一层
e1 = self.enc1(x) # [B, 64, H-, W-] -> [B, 64, H-4, W-4]
p1 = self.pool1(e1) # [B, 64, H-4, W-4] -> [B, 64, (H-4)/2, (W-4)/2]
# 第二层
e2 = self.enc2(p1) # [B, 64, (H-4)/2, (W-4)/2] -> [B, 128, (H-4)/2-4, (W-4)/2-4]
p2 = self.pool2(e2) # [B, 128, (H-4)/2-4, (W-4)/2-4] -> [B, 128, (H-4)/4-2, (W-4)/4-2]
# 第三层
e3 = self.enc3(p2) # [B, 128, (H-4)/4-2, (W-4)/4-2] -> [B, 256, (H-4)/4-6, (W-4)/4-6]
p3 = self.pool3(e3) # [B, 256, (H-4)/4-6, (W-4)/4-6] -> [B, 256, (H-4)/8-3, (W-4)/8-3]
# 第四层
e4 = self.enc4(p3) # [B, 256, (H-4)/8-3, (W-4)/8-3] -> [B, 512, (H-4)/8-7, (W-4)/8-7]
p4 = self.pool4(e4) # [B, 512, (H-4)/8-7, (W-4)/8-7] -> [B, 512, (H-60)/16, (W-60)/16]
# 瓶颈层
bottleneck = self.bottleneck(p4) # [B, 512, (H-60)/16, (W-60)/16] -> [B, 1024, (H-124)/16, (W-124)/16]
# 解码器(含跳跃连接)
# 上采样4层
up4 = self.upconv4(bottleneck) # [B, 1024, (H-124)/16, (W-124)/16] -> [B, 512, (H-124)/8, (W-124)/8]
e4_cropped = self._crop_and_concat(e4, up4) # 裁剪编码器特征图 e4 以匹配上采样特征图 up4 尺寸
merge4 = torch.cat([e4_cropped, up4], dim=1) # 拼接,[B, 512, (H-124)/8, (W-124)/8] -> [B, 1024, (H-124)/8, (W-124)/8]
d4 = self.dec4(merge4) # [B, 1024, (H-124)/8, (W-124)/8] -> [B, 512, (H-156)/8, (W-156)/8]
# 上采样3层
up3 = self.upconv3(d4) # [B, 512, (H-156)/8, (W-156)/8] -> [B, 256, (H-156)/4, (W-156)/4]
e3_cropped = self._crop_and_concat(e3, up3)
merge3 = torch.cat([e3_cropped, up3], dim=1) # [B, 256, (H-156)/4, (W-156)/4] ->[B, 512, (H-156)/4, (W-156)/4]
d3 = self.dec3(merge3) # [B, 512, (H-156)/4, (W-156)/4] -> [B, 256, (H-172)/4, (W-172)/4]
# 上采样2层
up2 = self.upconv2(d3) # [B, 256, (H-172)/4, (W-172)/4]-> [B, 128, (H-172)/2, (W-172)/2]
e2_cropped = self._crop_and_concat(e2, up2)
merge2 = torch.cat([e2_cropped, up2], dim=1) # [B, 128, (H-172)/2, (W-172)/2]-> [B, 256, (H-172)/2, (W-172)/2]
d2 = self.dec2(merge2) # [B, 256, (H-172)/2, (W-172)/2]-> [B, 128, (H-180)/2, (W-180)/2]
# 上采样1层
up1 = self.upconv1(d2) # [B, 128, (H-180)/2, (W-180)/2]-> [B, 64, H-180, W-180]
e1_cropped = self._crop_and_concat(e1, up1)
merge1 = torch.cat([e1_cropped, up1], dim=1) # [B, 64, H-180, W-180]-> [B, 128, H-180, W-180]
d1 = self.dec1(merge1) # [B, 128, H-180, W-180]-> [B, 64, H-184, W-184]
# 输出层
output = self.out_conv(d1) # [B, 64, H-184, W-184] -> [B, out_channels, H-184, W-184]
return output在U-Net中,由于编码器使用无填充卷积,特征图的尺寸会逐渐缩小,在解码器中,又通过上采样恢复特征图尺寸。此时,编码器与解码器对应层的特征图尺寸可能不一致,进而导致二者无法通过跳跃连接拼接起来。故需要对编码器的特征图进行裁剪,使其与上采样后的特征图尺寸一致。其代码如下:(具体调用在上面代码的前向传播过程中)
python
# 裁剪函数
def _crop_and_concat(self, encoder_feature, decoder_feature):
# 获取并计算输入特征图尺寸差异
delta_h = encoder_feature.size()[2] - decoder_feature.size()[2] # 高
delta_w = encoder_feature.size()[3] - decoder_feature.size()[3] # 宽
# 计算裁剪边界(顶部、底部、左侧、右侧)
top = delta_h // 2
bottom = delta_h - top
left = delta_w // 2
right = delta_w - left
# 应用裁剪
cropped = encoder_feature[:, :,
top: encoder_feature.size()[2] - bottom,
left: encoder_feature.size()[3] - right]
return cropped1.2 数据增强
数据增强部分主要是弹性形变的实现。它的原理是通过生成平滑的随机位移场来模拟生物组织的自然形变,能够在在医学图像数据有限的情况下,有效扩充训练集,也是 U-Net 能够在少量标注数据下取得优异性能的关键之一。
它主要包括两个参数, 控制形变的幅度,
控制形变的平滑程度。由于真实生物组织的变形通常服从高斯分布,且其具有良好的平滑性,故采用高斯分布生成随机位移。
python
class ElasticDeformation:
# 初始化
def __init__(self, alpha=10, sigma=5):
self.alpha = alpha # 位移场的强度
self.sigma = sigma # 位移场的高斯滤波标准差
# 应用
def __call__(self, image, mask=None):
H, W = image.shape[:2] # 获取图像的高与宽
# 在粗网格上生成随机位移场
grid_size = 3 # 网格尺寸 3x3
# 创建坐标,meshgrid 主要创建坐标网格,返回每个位置的x坐标与y坐标
grid_x, grid_y = np.meshgrid(
np.linspace(0, H, grid_size), # 生成 grid_size 个点,均匀分布在[0, H]区间
np.linspace(0, W, grid_size)
)
# 生成随机位移 (np.random.randn,从标准正态分布中生成随机数)
displacement_x = np.random.randn(grid_size, grid_size) * self.alpha
displacement_y = np.random.randn(grid_size, grid_size) * self.alpha
# 使用双三次插值将位移场扩展到图像尺寸
points = (np.linspace(0, H, grid_size), np.linspace(0, W, grid_size))
# 创建插值器
interp_x = RegularGridInterpolator(points, # 网格点坐标
displacement_x, # 网格点上的值
method='cubic', # 双三次插值
bounds_error=False, # 允许超出边界的查询
fill_value=0 # 超出边界时填充0
)
interp_y = RegularGridInterpolator(points, displacement_y,
method='cubic', bounds_error=False,
fill_value=0)
# 生成图像坐标网格
coords_x, coords_y = np.meshgrid(np.arange(H), np.arange(W), indexing='ij')
coords = np.stack([coords_x.ravel(), coords_y.ravel()], axis=1)
# 计算每个像素的位移
dx = interp_x(coords).reshape(H, W)
dy = interp_y(coords).reshape(H, W)
# 应用位移
map_x = coords_x + dx
map_y = coords_y + dy
# 确保坐标在边界内
map_x = np.clip(map_x, 0, H-1)
map_y = np.clip(map_y, 0, W-1)
# 重映射图像
if len(image.shape) == 2: # 灰度图像
# map_coordinates 实现逆向映射,即对于输出图像的每个位置,找到输入图像中对应的位置
deformed_image = map_coordinates(image, # 原始图像
[map_x, map_y], # 坐标映射
order=3, # 双三插值
mode='reflect' # 边界处理方式为反射填充
)
else: # 彩色图像
deformed_image = np.stack([
map_coordinates(image[:, :, c], [map_x, map_y], order=3, mode='reflect')
for c in range(image.shape[2])
], axis=2)
# 掩码处理,采用最近邻插值,保持标签完整
if mask is not None:
deformed_mask = map_coordinates(mask, [map_x, map_y], order=0, mode='reflect') # 最近邻插值
return deformed_image, deformed_mask
return deformed_image插值是根据已知离散点的数据来估计未知点的值。双三次插值是一种二维插值方法,它通过一个多项式来逼近函数,这个多项式是三次的,并且在两个维度上都进行三次插值;最近邻插值则是最简单、最快的插值方法,主要是对于目标图像中的每个像素,找到源图像中距离最近的像素,然后直接使用该像素的值。
2 Sinkhorn 算法实操
本节主要基于上周对Sinkhorn算法的学习对其进行手动计算理解与代码编写。
2.1 手动计算迭代

上图中,由源分布控制行约束,目标分布控制列约束,这一点与上周的学习相反。实际上,行与列并非指定分布进行约束,二者是平等的,算法只需根据成本矩阵来交替更新行和列的缩放因子,使两个边际约束同时满足即可。
2.2 代码
python
import numpy as np
def sinkhorn_knopp(r, c, M, reg=0.1, max_iter=1000, tol=1e-6):
"""
r: 行分布 (源分布) c: 列分布 (目标分布) M: 代价矩阵
reg: 正则化参数
max_iter: 最大迭代次数
tol: 收敛容差
"""
m, n = M.shape
# 归一化分布(确保和为1)
r = r / r.sum()
c = c / c.sum()
# 计算核矩阵 K = exp(-M/reg)
K = np.exp(-M / reg)
# 初始化缩放因子
u = np.ones(m) / m
v = np.ones(n) / n
# 迭代过程
for it in range(max_iter):
# 保存旧的v用于收敛检查
v_old = v.copy()
# 更新u
K_v = K @ v
u = r / (K_v + 1e-16) # 加一个小数防止除零
# 更新v
K_u = K.T @ u
v = c / (K_u + 1e-16)
# 检查收敛性
if np.linalg.norm(v - v_old) < tol:
print(f"在第 {it+1} 次迭代收敛")
break
# 计算传输矩阵 P = diag(u) @ K @ diag(v)
P = np.diag(u) @ K @ np.diag(v)
return P
# 测试函数
print("=== Sinkhorn算法示例 ===")
# 定义两个不同的分布
r = np.array([4, 6]) # 源分布
c = np.array([3, 2, 5]) # 目标分布
# 代价矩阵 (2x3)
M = np.array([[1, 2, 3],
[4, 1, 2]])
# 运行Sinkhorn算法
reg = 0.5 # 正则化参数
P = sinkhorn_knopp(r, c, M, reg=reg, max_iter=50)
print(f"传输矩阵 P:\n{P}")
# 验证行和列和
print(f"\n验证结果:")
print(f"P的行和: {P.sum(axis=1)} (应接近 {r/r.sum()})")
print(f"P的列和: {P.sum(axis=0)} (应接近 {c/c.sum()})")
# 计算传输成本
total_cost = np.sum(P * M)
print(f"总传输成本: {total_cost:.4f}")运行结果如下图所示:
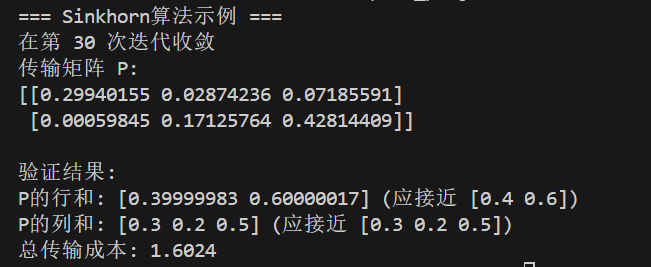
结果中打印输出行和和列和均小于 1 是由于在前面进行了归一化操作,实际并不影响算法效果。
另外,代码中引入了参数 tol (收敛容差),这个参数的作用在于判断算法是否已经足够接近真实解,会告诉算法什么时候停止迭代。它通常基于不同的精度需求进行选择,如果需要快速计算,精度可以较低,通常会设置为 1e-3;上述代码是要求中精度,故设置为 1e-6;如果对精度要求比较高,速度不是很重要,则可设置为 1e-9。
3 总结
本周主要对上周学习的内容,即 U-Net 与 Sinkhorn 算法进行了梳理,更加深入了解了前者的网络结构与后者的实现,同时通过手动计算对 Sinkhorn 算法的迭代有了更清晰的认识。此外接触到了插值这种处理数据的方法,感觉下周可以拓展了解一下。