算法剖析1：摩尔投票算法 ——寻找出现次数超过一半的数

一、算法概述

在算法面试和刷题中，我们经常会遇到这样一类问题：在一个数组中找到出现次数超过一半的元素。如果用暴力统计或者哈希表的方法，虽然能解决问题，但要么时间复杂度高，要么空间复杂度不够理想。今天我要给大家介绍的摩尔投票法（Boyer-Moore Majority Vote Algorithm），正是解决这类问题的 "最优解"，它可以在 O(N) 时间复杂度和 O(1) 空间复杂度内找到答案。

二、问题背景

现在给你一个长度为n的数组，有一个数出现次数最多，请你设计一个算法找出这个数。

这道题的核心就是 "找多数元素"------ 即出现次数最多的元素唯一。题目保证这样的元素一定存在，这也是摩尔投票法能够生效的前提条件。

方案一：暴力统计

数据量大时，容易超时

方案二；哈希法

空间开销大

方案三：摩尔投票法

完美解决

三、算法理解

想象一下，你现在来到一个新的班级，年级主任要求你们班必须得有一个班长，并且现在就得选出来。而你作为班主任，在不知道谁更适合的情况下，你会怎么做呢？你会这样做，从序号为1同学开始，让每个人开始当班长。按以下规则筛选：

令临时班长=张三可靠度=1（默认选择相信他）

1.如果当前班长没有可靠度，换人 //滚蛋

2.如果临时班长被人投诉，可靠度-1；//支持

3.如果临时班长干的还不错，表扬一波，可靠度+1；//不支持

四、算法原理

由于题目保证存在一个数字出现次数最多，我们可以通过 "抵消" 的思想来找到这个数。
维护一个候选数 candidate 和一个计数器 count。
遍历矩阵中的每个元素：
- 如果 count == 0，就将当前元素设为候选数。
- 如果当前元素等于候选数，count++；否则，count--。
最终剩下的候选数就是出现次数超过一半的数。

五、算法实现

令 currNum=？（暂时不知道），count=0

遍历数组：（int a $n$ ）

(假设当前数为a $i$ )

if(count==0)

{

currNum=a $i$ ;

count++;//默认投支持票

}

else if(currNum==a $i$ )count++;

else if(currNum!=a $i$ )count--;

这样们就可以找到出现次数最多的元素了

六、真题实解

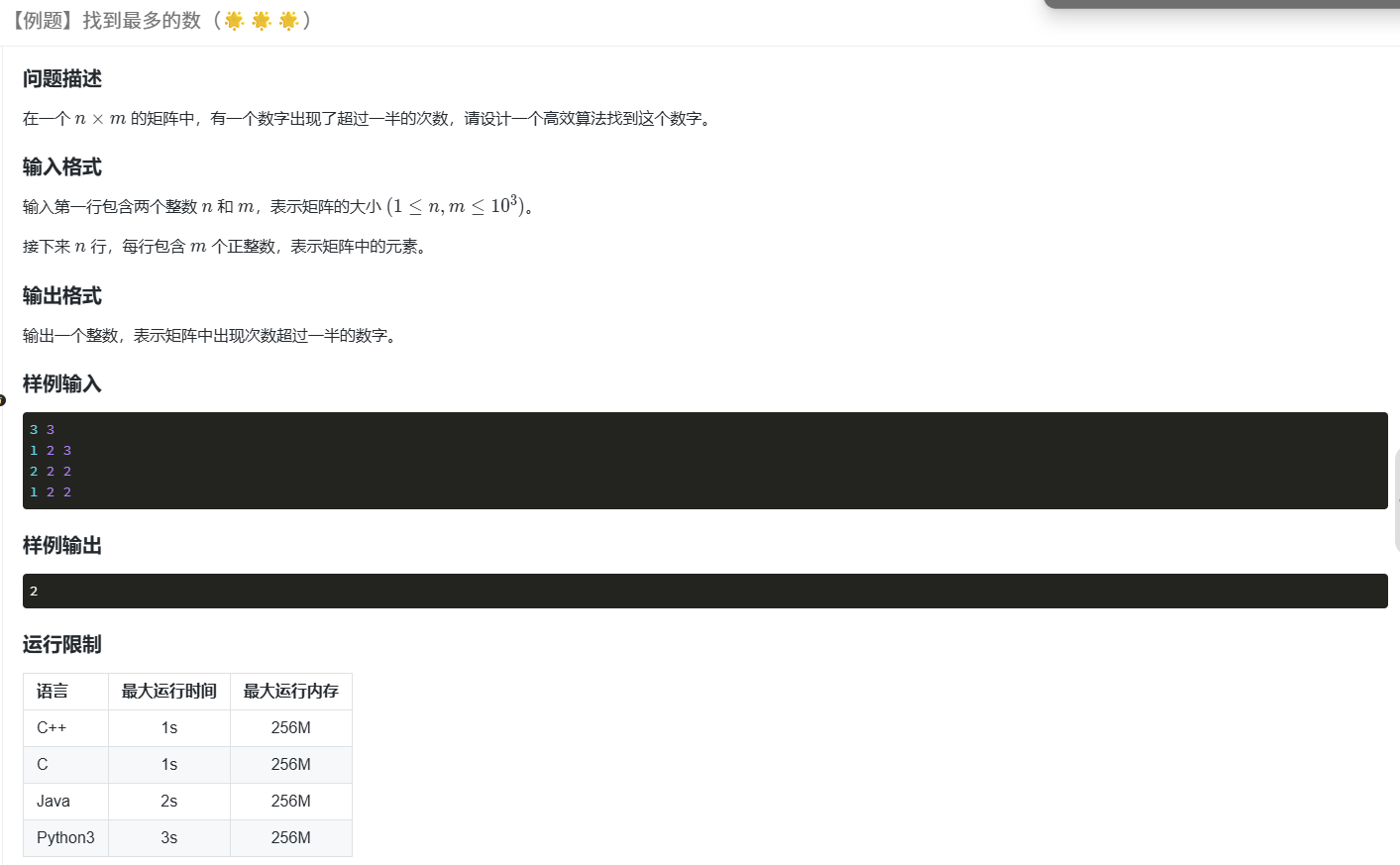
代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std; 

int main()
{
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int n,m;
	cin>>n>>m;
	int count=0;
	int wait;
	for(int i=0;i<n;i++)for(int j=0;j<m;j++)
	{
		int x;
		cin>>x;
		if(count==0)
    {
      wait=x;
      count++;
    }
		else if(wait==x)count++;
		else if(wait!=x)count--;
	}
	cout<<wait<<endl;
	return 0;
}