几何直觉与概率流动的交响：深度解析《理解深度学习》的重构之美

文章目录

几何直觉与概率流动的交响：深度解析《理解深度学习》的重构之美
- [一、第一性原理：从高维空间的"折叠"开始（第3-5章）](#一、第一性原理：从高维空间的“折叠”开始（第3-5章）)
- - [1.1 浅层网络的几何解构](#1.1 浅层网络的几何解构)
- [二、核心引擎：优化曲面与泛化的悖论（第8-9章）](#二、核心引擎：优化曲面与泛化的悖论（第8-9章）)
- - [2.1 为什么随机梯度下降（SGD）如此有效？](#2.1 为什么随机梯度下降（SGD）如此有效？)
  - [2.2 双下降（Double Descent）与过拟合](#2.2 双下降（Double Descent）与过拟合)
- [三、架构革命：Transformer 的全局路由机制（第12章）](#三、架构革命：Transformer 的全局路由机制（第12章）)
- - [3.1 自注意力：从数学到拓扑](#3.1 自注意力：从数学到拓扑)
  - [3.2 架构性能的深度对比](#3.2 架构性能的深度对比)
- [四、代码实战：解构多头注意力（Multi-Head Attention）](#四、代码实战：解构多头注意力（Multi-Head Attention）)
- [五、前沿探索：生成模型的概率魔法（第14-16章）](#五、前沿探索：生成模型的概率魔法（第14-16章）)
- - [5.1 从加噪到去噪](#5.1 从加噪到去噪)
- [六、综合评价与推荐](#六、综合评价与推荐)

几何直觉与概率流动的交响：深度解析《理解深度学习》的重构之美

------评清华大学出版社引进版 Understanding Deep Learning

在人工智能席卷全球的今天，深度学习（Deep Learning）早已从学术界的象牙塔走向了工业界的生产线。然而，对于广大从业者和求学者而言，横亘在"调包侠"与"算法科学家"之间有一道巨大的鸿沟：前者知其然而不知其所以然，往往迷失在超参数调整的玄学中；后者则容易陷入枯燥的公式推导，忽视了模型背后的几何直觉。

清华大学出版社近期引进的、由 Simon J.D. Prince 教授撰写的《理解深度学习》（Understanding Deep Learning ），正是填平这道鸿沟的完美"桥梁"。这不仅是一本教材，更是一部试图用几何学 和概率论重新解释智能本质的宏伟著作。通读全书，我被其严谨的逻辑闭环与惊艳的视觉化表达深深折服。以下将从第一性原理、核心架构、前沿生成模型及工程实践四个维度，对本书进行深度赏析。

一、第一性原理：从高维空间的"折叠"开始（第3-5章）

大多数深度学习教材习惯从生物神经元讲起，而本书则选择了一条更为数学化的路径------函数近似（Function Approximation）。作者开宗明义地提出：神经网络本质上是一个参数极其庞大的函数，其目的是在只有有限采样点（训练数据）的情况下，拟合出一个高维流形。

1.1 浅层网络的几何解构

书中对于"浅层神经网络"的讲解堪称经典。作者没有堆砌的公式，而是引导读者思考：一个简单的 ReLU 激活函数究竟对输入空间做了什么？

通过这种几何视角的拆解，读者会恍然大悟：原来增加神经网络的"宽度"，是在增加对输入空间的切分粒度；而增加"深度"，则是在对空间进行反复的折叠与拉伸。这种直观的认知，为后续理解为什么深层网络比宽层网络更高效奠定了坚实基础。

二、核心引擎：优化曲面与泛化的悖论（第8-9章）

如果说网络架构是骨架，那么优化算法就是注入灵魂的过程。本书在第8章探讨了**损失函数曲面（Loss Landscape）**的性质，这部分内容的专业度远超一般入门书籍。

2.1 为什么随机梯度下降（SGD）如此有效？

作者深入探讨了一个反直觉的现象：在非凸优化中，我们本应极易陷入局部最优解，但神经网络却往往能收敛到很好的解。书中通过 Hessian 矩阵的特征值分析指出，高维空间中真正的"局部极小值"其实很少，绝大多数梯度为零的点是鞍点（Saddle Points）。

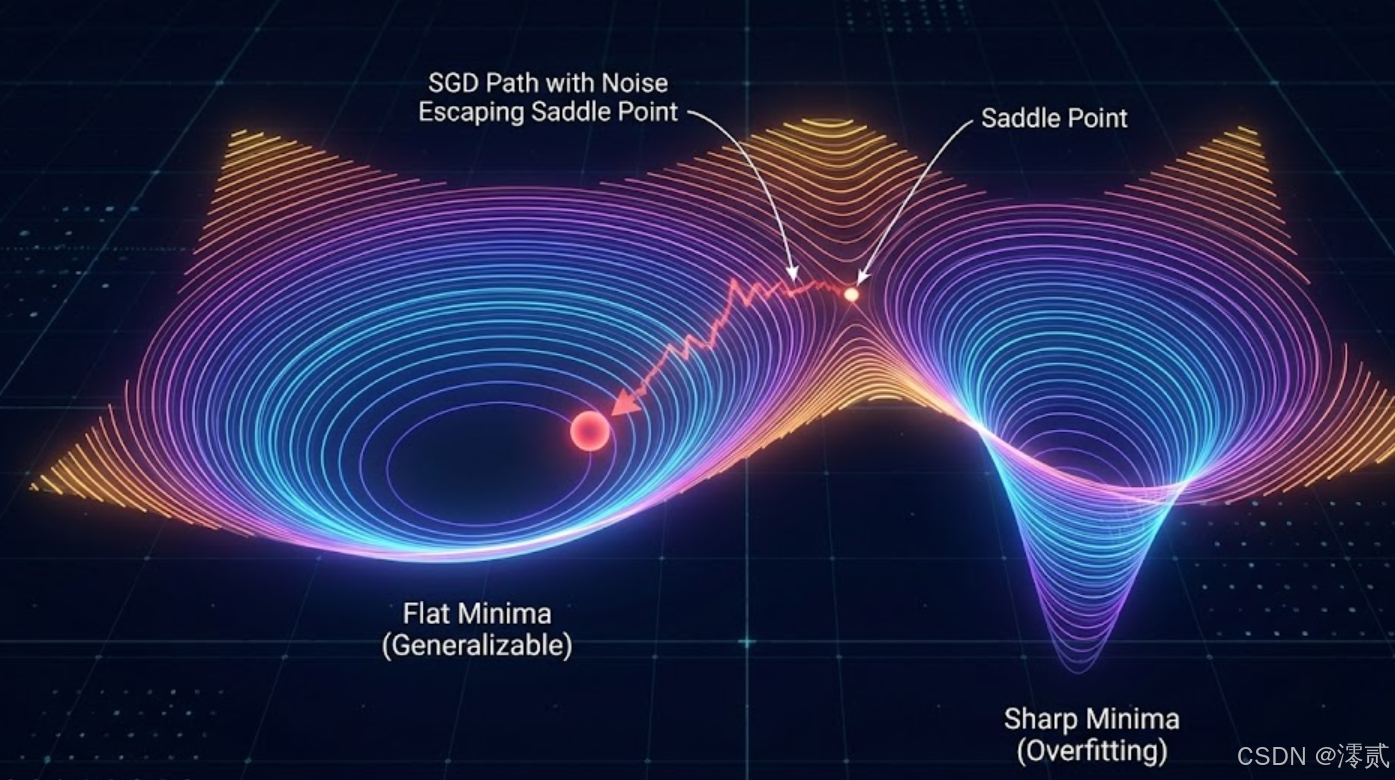
2.2 双下降（Double Descent）与过拟合

在第9章，作者触及了现代深度学习最核心的谜题------双下降现象。传统统计学习理论认为，参数过多会导致过拟合。但在深度学习中，当参数量远超数据量时，测试误差反而会再次下降。本书通过"偏差-方差分解"的现代视角，解释了深度模型实际上是在寻找一种"平滑的插值解"，这种深刻的洞察力是本书的一大亮点。

三、架构革命：Transformer 的全局路由机制（第12章）

本书第12章对 Transformer 的解析，是我读过的所有资料中最为透彻的。作者并未停留在架构图的层面，而是将其定义为一种基于内容的动态寻址系统。

3.1 自注意力：从数学到拓扑

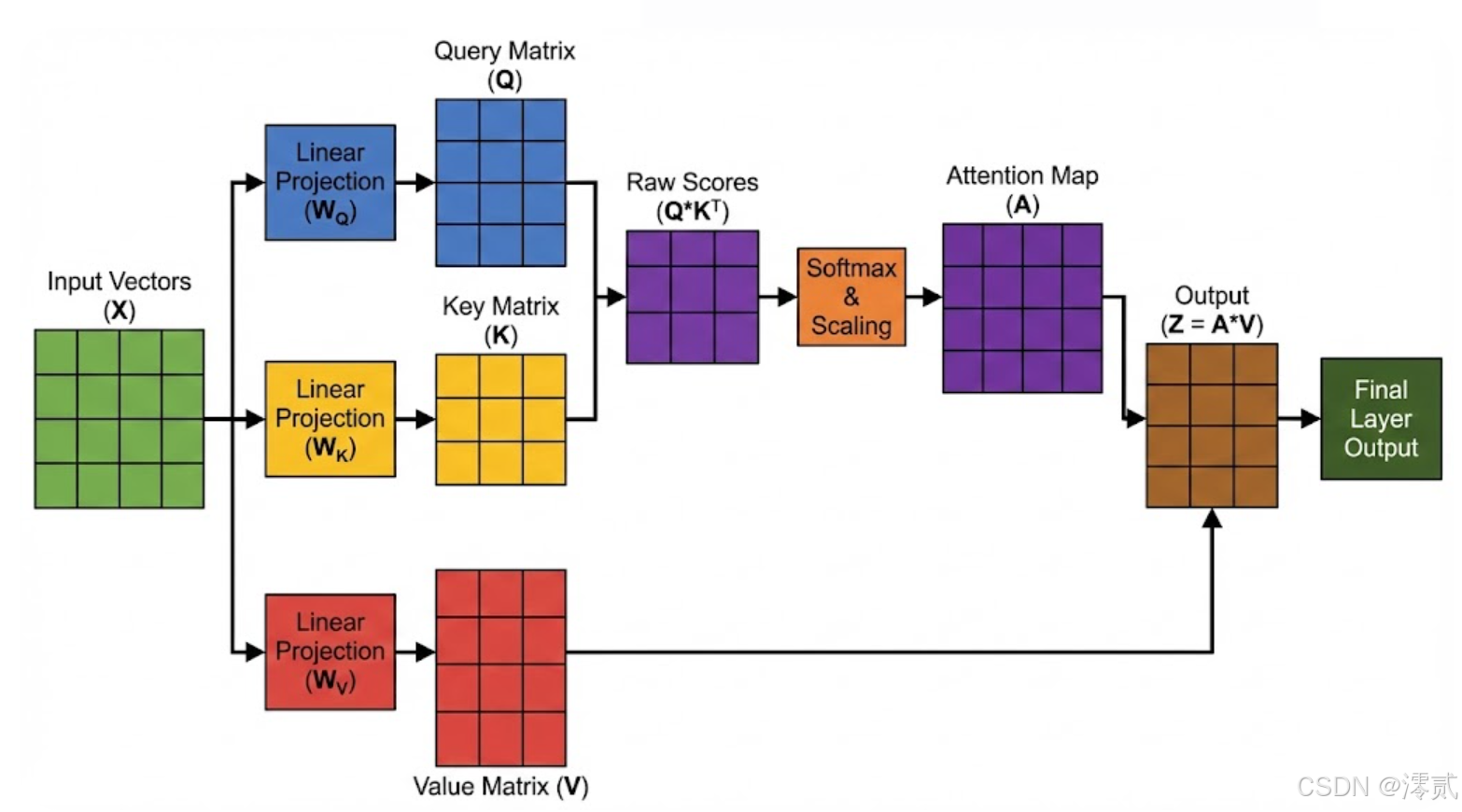
不同于 CNN 的局部感受野和 RNN 的时序依赖，Transformer 利用点积相似度，彻底消除了序列中物理距离的限制。书中通过以下公式，精妙地阐述了 Query-Key-Value 的交互逻辑：

作者特别强调了缩放因子的重要性：它不是一个随意的常数，而是为了对抗高维空间中向量点积方差爆炸的数学修正。没有这个修正，Softmax 将进入梯度饱和区，导致训练停滞。

3.2 架构性能的深度对比

为了让读者理解 Transformer 为何能统治 NLP 乃至 CV 领域，书中列举了不同架构的归纳偏置（Inductive Bias）对比，如下表所示：

架构特性	循环神经网络 (RNN)	卷积神经网络 (CNN)	Transformer (Self-Attention)
计算复杂度
并行效率	低（必须串行处理）	高（滑动窗口独立）	极高（全序列并行）
长程依赖能力	弱（梯度路径随长度线性增长）	中（受限于网络深度和核大小）	强（任意两点路径为）
位置感知	内置（顺序处理隐含位置）	局部相对位置	无（必须显式引入位置编码）
归纳偏置	时间平移不变性	空间局部性	弱偏置（完全依赖数据驱动）

四、代码实战：解构多头注意力（Multi-Head Attention）

本书的一大特色是"理论与实践的零距离"。作者提供的代码不仅仅是调用 PyTorch API，而是展示了张量变换的底层逻辑。以下是基于书中最核心思想复现的多头注意力代码，它展示了模型如何并行地在不同"子空间"中捕获特征：

python 复制代码

import torch
import torch.nn as nn
import torch.nn.functional as F

class MultiHeadAttention(nn.Module):
    """
    基于《理解深度学习》第12章原理实现
    核心思想：将高维特征拆分为 h 个子空间，分别计算注意力，捕捉多重语义关联
    """
    def __init__(self, d_model, num_heads):
        super().__init__()
        assert d_model % num_heads == 0
        
        self.d_k = d_model // num_heads  # 每个头的维度
        self.h = num_heads               # 头的数量
        
        # 定义线性投影层：将输入映射到 Q, K, V 空间
        self.w_queries = nn.Linear(d_model, d_model)
        self.w_keys = nn.Linear(d_model, d_model)
        self.w_values = nn.Linear(d_model, d_model)
        
        # 输出层的线性投影
        self.fc_out = nn.Linear(d_model, d_model)

    def forward(self, x, mask=None):
        batch_size, seq_len, _ = x.size()
        
        # 1. 线性映射并重塑维度，实现多头并行
        # 变换后维度: (batch, heads, seq_len, d_k)
        # transpose(1, 2) 是为了让 heads 维度在 seq_len 之前，方便后续矩阵乘法
        Q = self.w_queries(x).view(batch_size, seq_len, self.h, self.d_k).transpose(1, 2)
        K = self.w_keys(x).view(batch_size, seq_len, self.h, self.d_k).transpose(1, 2)
        V = self.w_values(x).view(batch_size, seq_len, self.h, self.d_k).transpose(1, 2)

        # 2. 计算缩放点积注意力 (Scaled Dot-Product Attention)
        # 矩阵乘法: (batch, h, seq_len, d_k) x (batch, h, d_k, seq_len) -> (batch, h, seq_len, seq_len)
        energy = torch.matmul(Q, K.transpose(-2, -1)) / (self.d_k ** 0.5)
        
        # 应用掩码（Masking），例如在解码器中屏蔽未来信息
        if mask is not None:
            energy = energy.masked_fill(mask == 0, float("-1e20"))

        # 归一化得到注意力权重
        attention = F.softmax(energy, dim=-1)
        
        # 3. 加权求和并拼接多头结果
        # (batch, h, seq_len, seq_len) x (batch, h, seq_len, d_k) -> (batch, h, seq_len, d_k)
        out = torch.matmul(attention, V)
        
        # 还原维度: (batch, seq_len, h * d_k) = (batch, seq_len, d_model)
        out = out.transpose(1, 2).contiguous().view(batch_size, seq_len, -1)
        
        return self.fc_out(out)

这段代码清晰地展示了 view 和 transpose 操作如何构建并行计算图，这是理解现代大模型训练效率的关键。

五、前沿探索：生成模型的概率魔法（第14-16章）

在 AIGC（生成式人工智能）爆发的背景下，本书对**扩散模型（Diffusion Models）**的讲解显得尤为珍贵。作者没有回避数学难度，而是正面迎击了"朗之万动力学"和"分数值匹配"等核心概念。

5.1 从加噪到去噪

书中通过马尔可夫链的视角，解释了扩散模型的工作原理：训练过程是学习如何逆转一个逐渐向数据添加高斯噪声的过程。

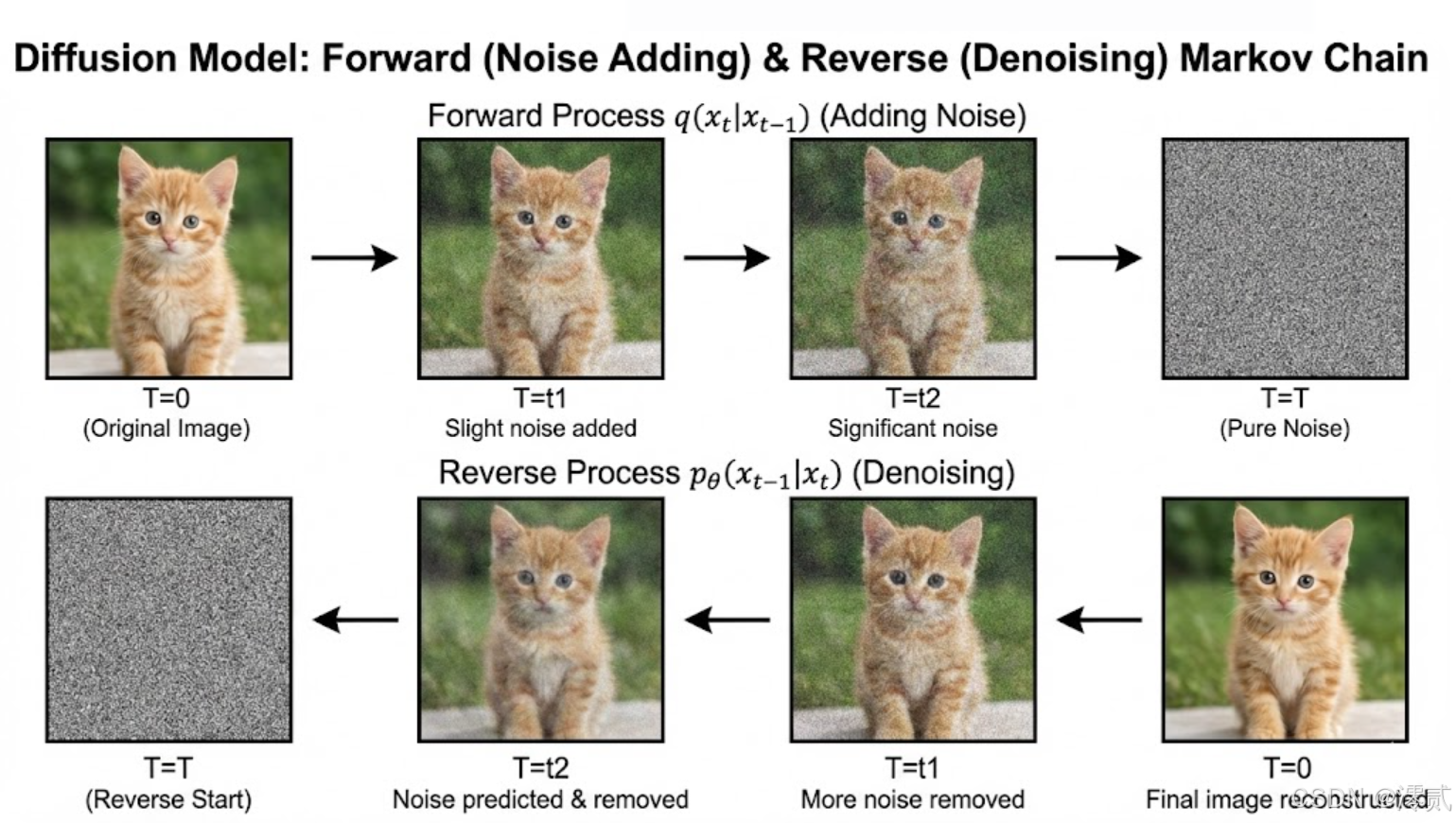
作者精彩地对比了 GAN（生成对抗网络）与 Diffusion 的区别：GAN 试图一次性映射噪声到图像，容易导致模式坍塌（Mode Collapse）；而 Diffusion 将这一困难任务分解为成百上千个微小的去噪步骤，从而极大地提升了生成的稳定性和多样性。

六、综合评价与推荐

通读全书，我深感《理解深度学习》是一本难得的"通透之作"。

视觉化的降维打击：本书最大的亮点在于拥有超过 500 幅高质量的全彩插图。作者 Simon Prince 坚信"一图胜千言"，他将复杂的矩阵运算、高维空间的流形变换、概率分布的演化，全部转化为具象的几何图形。这种视觉化表达极大地降低了认知负荷，让读者能够在大脑中建立起清晰的物理模型。
严谨与通俗的平衡：清华大学出版社引进的这个版本，翻译质量极高，保留了原汁原味的学术精确性。书中既有直觉式的解释，也有严谨的数学推导（如变分下界的推导），适合不同层次的读者各取所需。
极强的时效性：不同于那些还停留在 LSTM 时代的旧教材，本书大幅篇幅涉及 Transformer、大规模预训练模型（LLMs）以及扩散模型，是目前市面上极少数能从底层原理讲清楚 GPT 和 Stable Diffusion 的教科书。

【总结推荐】

如果你是在校大学生：这本书能帮你从根本上理解微积分和线性代数在 AI 中的实际意义，建立扎实的理论地基。
如果你是算法工程师：书中对优化算法、正则化策略和架构偏置的深度剖析，将直接提升你设计模型和排查 Bug 的直觉与能力。
如果你是科研人员：书中对生成模型概率框架的统一视角，或许能为你的下一个研究课题提供灵感。

《理解深度学习》不仅教会我们如何构建智能体，更教会我们如何像数学家一样思考高维世界。它值得被摆在每一位 AI 从业者书桌最显眼的位置。

几何直觉与概率流动的交响：深度解析《理解深度学习》的重构之美

文章目录