Leecode热题100：环形链表（链表）

题目描述：

回归本质 (Deconstruction)

寻找切入点 (The Insight)

逻辑推演 (Deduction)

[C++ 代码实现 (Construction)](#C++ 代码实现 (Construction))

面试回答

[1. 揭示本质冲突](#1. 揭示本质冲突)

[2. 引入物理模型：相对运动](#2. 引入物理模型：相对运动)

[3. 推导参数的选择](#3. 推导参数的选择)

[4. 描述执行过程](#4. 描述执行过程)

变体：找到环的"入口节点"

变量化本质 (Mathematical Deconstruction)

建立逻辑恒等式 (The Logical Identity)

翻译数学为算法 (The "Aha!" Moment)

[C++ 代码实现(Construction)](#C++ 代码实现(Construction))

题目描述：

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

示例 1：

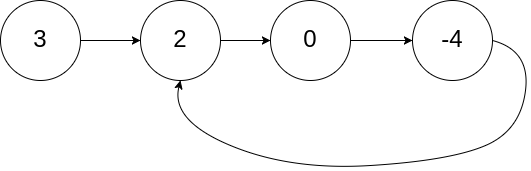
输入：head = [3,2,0,-4], pos = 1

输出：true

解释：链表中有一个环，其尾部连接到第二个节点。

（来源：Leecode）

回归本质 (Deconstruction)

1. 链表的物理事实是什么？

单链表是一个单向流动的结构，每个节点只知道"下一步"在哪。
正常链表：像一条射线，终点是 nullptr。
带环链表：像一个操场跑道，一旦进入环，就永远没有终点，只能不断循环。

2. 核心矛盾是什么？ 如果我们像普通的遍历那样一直走下去：

如果没有环，我们会撞到终点（nullptr），程序停止。
如果有环，程序会陷入无限死循环。
问题在于： 计算机无法仅凭"一直在走"就判定"我进入了环"，因为它不知道前面是否还有一个极长的链。

寻找切入点 (The Insight)

如何证明自己在"兜圈子"？

方案 A：记忆法（哈希表）

逻辑：拿个小本本记下走过的每个节点的地址。每走一步，查一下本子。
代价：需要额外的空间（O(n)）来存放记录。如果面试官要求空间复杂度为 O(1)（不准用小本本），我们该怎么办？

方案 B：相对速度法 （第一性原理的突破）回到物理世界的直觉：在操场上跑步。

如果两个人在直路上跑，速度快的人只会越跑越远，永远不会相遇。
如果在环形操场上跑，速度快的人（快指针）一定会在某一时刻"套圈"那个速度慢的人（慢指针）。

底层真理：在一个有限的循环空间内，两个具有速度差的物体必然会相遇。

逻辑推演 (Deduction)

我们要设计两个指针：

慢指针 (Slow)：每次走 1 步。
快指针 (Fast)：每次走 2 步。

为什么快指针走 2 步，而不是 3 步或 100 步？

从第一性原理考虑：快指针相对于慢指针的相对速度是 1 步/次。
这意味着在环内，每移动一次，它们之间的距离就缩短 1。
距离从 N, N-1, ..., 1，最终变为 0。它们一定会精确地在某个节点相遇，而不会直接跳过去。

C++ 代码实现 (Construction)

让我们用 C++ 把这个逻辑变成现实。

cpp 复制代码

class Solution {
public:
    bool hasCycle(ListNode *head) {
        // 第一性原理：空链表或只有一个节点的链表不可能有环
        if (head == nullptr || head->next == nullptr) {
            return false;
        }

        // 初始化：两名运动员在起点准备
        ListNode *slow = head;
        ListNode *fast = head;

        // 只要快指针没跑到终点，比赛就继续
        while (fast != nullptr && fast->next != nullptr) {
            slow = slow->next;          // 慢指针走 1 步
            fast = fast->next->next;    // 快指针走 2 步

            // 核心逻辑：如果相遇，说明存在环
            if (slow == fast) {
                return true;
            }
        }

        // 如果跳出了循环，说明快指针撞到了终点 (nullptr)
        return false;
    }
};

1. 时间复杂度：

如果没有环，快指针走 n/2 步到达终点。
如果有环，快指针进入环后，最多在 n 步内追上慢指针。
结论：O(n)。

2. 空间复杂度：

我们只使用了两个指针变量，没有开启额外的存储空间。
结论：O(1)。

面试回答

1. 揭示本质冲突

首先，指出单链表检测环的特殊性：

"检测链表是否有环，核心难点在于'信息的有限性'。由于单链表只能向后看，如果我们只用一个指针遍历，当它进入环路后，它无法分辨自己是在走一段极长的路，还是在重复走过的路。

除非我们记录下所有走过的节点地址（哈希表），但这会消耗 O(n) 的空间。所以，我们需要一个不需要记忆就能证明'重复'的物理模型。"

2. 引入物理模型：相对运动

通过生活中的常识引入算法逻辑，这会让面试官觉得你对算法有直观的理解：

"我借鉴了**'操场套圈'**的逻辑。在环形跑道上，两个速度不同的人从同一点出发，跑得快的人必然会领先慢的人一整圈，从而实现'追尾'。

这里的底层逻辑是：在闭合环路中，相对速度会导致距离的周期性重合。"

3. 推导参数的选择

这是一个高阶技巧，解释为什么快指针步长选 2：

"为了实现这个模型，我设置了两个指针：慢指针 slow 每次走 1 步，快指针 fast 每次走 2 步。

为什么要选 2 步？因为从第一性原理分析，快指针相对于慢指针的相对速度是 2 - 1 = 1。

这意味着，一旦两个指针都进入环内，它们之间的距离每移动一次就会缩小 1。由于步长差是 1，它们一定会相遇而不会跳过彼此。如果快指针选 3 步或更多，理论上它们可能在某些小环中'擦肩而过'，需要更多逻辑去判断。"

4. 描述执行过程

简洁地概括代码的行为：

"在执行过程中：

如果 fast 最终指向了 nullptr 或其 next 为空，说明链表是有终点的，无环。

如果在某一时刻 fast == slow，则证明快指针完成了'套圈'，必有环。

这个算法的时间复杂度是 O(n)，空间复杂度是 O(1)，它是检测环路的最优解。"

💡 面试官可能的深度追问

追问：如果快指针每次走 3 步，慢指针走 1 步，一定会相遇吗？

"在连续的空间里一定会，但在链表这种离散节点的空间里，不一定能'立即'相遇。

相对速度为 2。假设环的长度是 L，进入环时两者距离为 D。每次移动距离缩小 2。

如果 D 是偶数，它们会相遇。

如果 D 是奇数，它们会跳过彼此，进入下一轮追逐。

只要 L 和相对速度 2 不是互质的（或者经过数学推导，在离散数学中这最终也会收敛），它们最终还是会相遇，但步长为 2 的相对速度（1）是最稳健的，因为它保证了距离每次减 1，绝不会跳过相遇点。"

变体：找到环的"入口节点"

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改链表。

寻找"环的入口节点"是算法面试中的经典难题。如果说判断是否有环靠的是物理直觉 （套圈），那么找入口节点靠的就是数学推导的必然性。

我们继续用第一性原理，从最本质的距离关系出发。

变量化本质 (Mathematical Deconstruction)

我们要找的是"入口点"，让我们把链表的路径拆解为三个物理长度：

a：从"头节点"到"环入口点"的距离。
b：从"环入口点"到"快慢指针相遇点"的距离（顺时针）。
c：从"相遇点"继续往前走，回到"环入口点"的距离。

由此可知，环的总长度 L = b + c。

建立逻辑恒等式 (The Logical Identity)

当快慢指针在环内相遇时，我们列出它们各自走过的总路程：

慢指针 (Slow) 走过的路程：S = a + b

(注：慢指针进入环的第一圈内必然会被快指针追上，所以它在环内走的距离不会超过一圈)
快指针 (Fast) 走过的路程：F = a + n(b + c) + b

(n 是快指针在环里转的圈数，因为快指针跑得快，可能转了好几圈才遇到慢指针)

第一性原理告诉我们： 快指针的速度是慢指针的两倍。

所以：F = 2S

带入公式：

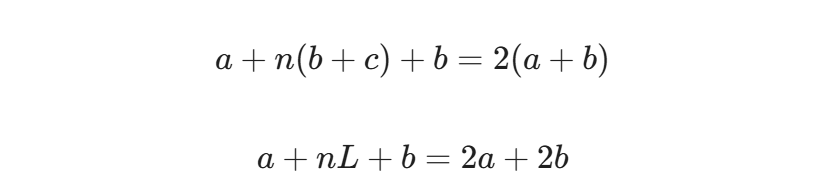
我们要找的是入口点，即求 a。我们将公式变形，孤立出 a：

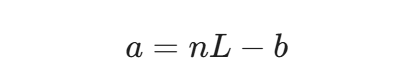
为了看清本质，我们从 nL 中借出一个 L（即 b+c）：

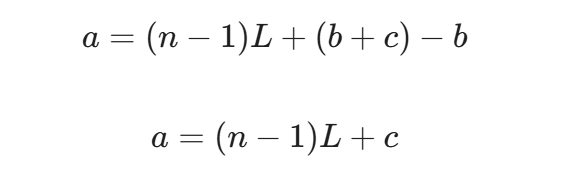
翻译数学为算法 (The "Aha!" Moment)

观察这个最终公式：

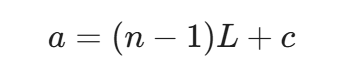
a：从"头节点"走到"入口点"的距离。
c：从"相遇点"走到"入口点"的距离。
(n-1)L：绕环转了整数圈。

结论：

如果你在快慢指针相遇后，把其中一个指针放回头节点 ，另一个留在相遇点，然后让它们以同样的速度（每次走 1 步）同时出发：

从头出发的指针走过 a 步到达入口。
从相遇点出发的指针走过 c 步，再转 n-1 圈，也会恰好到达入口！

它们一定会在入口点"相撞"。

C++ 代码实现(Construction)

cpp 复制代码

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if (head == nullptr || head->next == nullptr) return nullptr;

        ListNode *slow = head;
        ListNode *fast = head;

        // 第一步：利用快慢指针寻找相遇点（判断是否有环）
        bool hasCycle = false;
        while (fast != nullptr && fast->next != nullptr) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) {
                hasCycle = true;
                break;
            }
        }

        // 如果没有环，根据第一性原理，直接返回 null
        if (!hasCycle) return nullptr;

        // 第二步：根据公式 a = (n-1)L + c
        // 让其中一个指针回到 head，另一个保持在相遇点
        slow = head;
        while (slow != fast) {
            // 两个指针同时匀速（1步）前进
            slow = slow->next;
            fast = fast->next;
        }

        // 它们相遇的地方就是入口点
        return slow;
    }
};