K 近邻算法(K-Nearest Neighbors,KNN)是一种基本的分类与回归方法,属于监督学习算法。其核心思想是通过计算给定样本与数据集中所有样本的距离,找到距离最近的 K个样本,然后根据这 K 个样本的类别或值来预测当前样本的类别或值
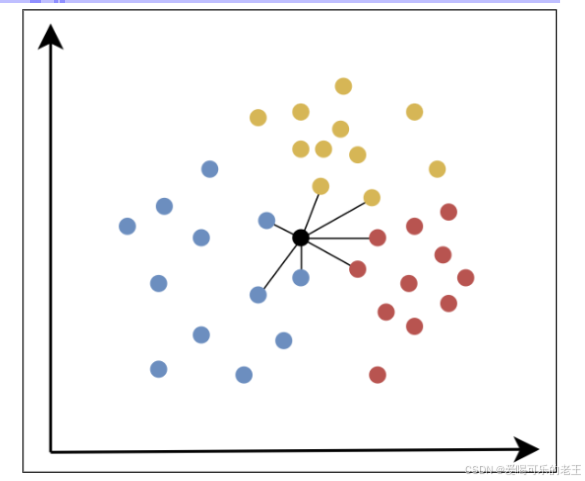
一、工作原理
- 计算距离:计算待预测样本与训练集中所有样本的特征距离(如欧氏距离、曼哈顿距离)。
- 筛选近邻:选取距离最近的 K 个样本(K 为超参数)。
- 决策预测:分类任务采用 "投票制"(K 个近邻中占比最高的类别为结果);回归任务采用 "平均制"(K 个近邻的数值均值为结果)。
二、关键要素
1. 距离度量方法(核心参数)
- 欧氏距离:最常用,两点间直线距离,适用于连续特征 且无异常值的场景。
- 曼哈顿距离:坐标差的绝对值之和,适用于高维数据 或存在异常值的场景。
- 切比雪夫距离:坐标差的最大值,适用于需关注极端差异的场景。
- 闵可夫斯基距离:通用形式,通过参数 p 适配不同距离(p=1 为曼哈顿距离,p=2 为欧氏距离)。
2. K 值选择(影响模型性能)
- K 值过小:易受噪声样本影响,导致过拟合(模型只适配训练数据,泛化能力差)。
- K 值过大:可能包含无关样本,导致欠拟合(模型无法捕捉数据规律)。
- 经验建议:K 通常取奇数(避免投票平局),需通过交叉验证优化。
3. 数据预处理(必做步骤)
KNN 对特征尺度敏感,需先进行预处理:
-
归一化:将特征缩放到固定范围(如 [0,1] 或 [-1,1]),适用于有明确边界的数据(如像素值)
#归一化
from sklearn.preprocessing import MinMaxScaler
X = [[2, 1], [3, 1], [1, 4], [2, 6]]归一化,区间设置为(-1,1)
X = MinMaxScaler(feature_range=(-1, 1)).fit_transform(X)
print(X) -
标准化:将特征转换为均值 0、标准差 1 的分布,适用于数据分布未知的场景,鲁棒性更强。
#标准化
from sklearn.preprocessing import StandardScaler
X = [[2, 1], [3, 1], [1, 4], [2, 6]]标准化
X = StandardScaler().fit_transform(X)
print(X)
三、优缺点分析
优点
- 逻辑简单:无需训练过程,直接用原始数据预测,易理解和实现。
- 适应性强:可处理分类和回归任务,对非线性数据有一定适配性。
- 实时更新:新增训练样本无需重新训练模型,直接加入数据集即可。
缺点
- 计算量大:预测时需遍历所有训练样本,数据量较大时速度较慢。
- 对噪声敏感:异常样本可能被选为近邻,影响预测结果。
- 高维灾难:特征维度过高时,距离度量的区分度会下降,模型性能变差。
四、适用场景
- 数据量较小、特征维度适中的场景(如小规模分类任务、简单回归预测)。
- 对模型可解释性要求高的场景(如医疗辅助诊断、小型推荐系统)。
- 实时性要求不高的场景(如离线数据分析、批量预测)。
五、核心 API 使用(Sklearn)
1. 分类任务
from sklearn.neighbors import KNeighborsClassifier
# 初始化模型(K=3)
knn_clf = KNeighborsClassifier(n_neighbors=3)
# 训练模型(无需复杂训练,本质是存储数据)
knn_clf.fit(X_train, y_train)
# 预测
y_pred = knn_clf.predict(X_test)2. 回归任务
from sklearn.neighbors import KNeighborsRegressor
# 初始化模型(K=2)
knn_reg = KNeighborsRegressor(n_neighbors=2)
# 训练模型
knn_reg.fit(X_train, y_train)
# 预测
y_pred = knn_reg.predict(X_test)六、实践技巧
- 数据预处理:优先使用标准化或归一化,消除特征量纲差异(如身高 "米" 和体重 "千克")。
- K 值优化:通过网格搜索 + 交叉验证(如 10 折交叉验证)选择最优 K 值(通常范围 1-10)。
- 降维处理:高维数据先通过 PCA 等方法降维,减少计算量并提升模型性能。
- 样本均衡:若数据类别不平衡,可对少数类样本加权,避免模型偏向多数类。