题目
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
数据范围
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
测试用例
示例1
java
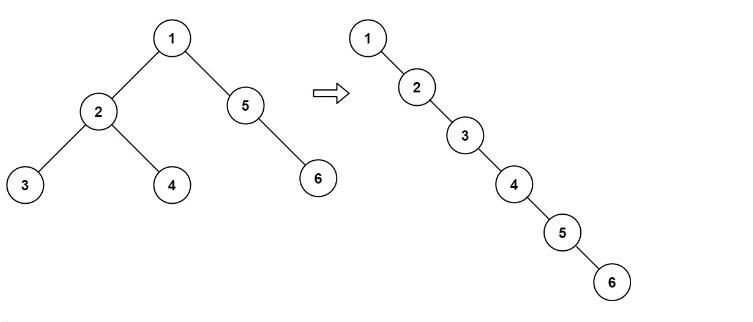
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]示例2
java
输入:root = []
输出:[]示例3
java
输入:root = [0]
输出:[0]题解(递归,前序遍历,时空On,会破坏结构)
java
class Solution {
public void flatten(TreeNode root) {
List<TreeNode> list = new ArrayList<TreeNode>();
preorderTraversal(root, list);
int size = list.size();
for (int i = 1; i < size; i++) {
TreeNode prev = list.get(i - 1), curr = list.get(i);
prev.left = null;
prev.right = curr;
}
}
public void preorderTraversal(TreeNode root, List<TreeNode> list) {
if (root != null) {
list.add(root);
preorderTraversal(root.left, list);
preorderTraversal(root.right, list);
}
}
}题解2(迭代,前序,时空On,不会破坏结构)
java
class Solution {
public void flatten(TreeNode root) {
if (root == null) {
return;
}
// 1. 使用 ArrayDeque,性能优于 LinkedList
// 2. 这里当作"栈"来使用
Deque<TreeNode> stack = new ArrayDeque<>();
stack.push(root);
TreeNode pre = null;
while (!stack.isEmpty()) {
// 弹出栈顶元素 (建议用 pop 对应 push)
TreeNode curr = stack.pop();
// 建立链表连接:上一个节点的 right 指向当前节点
if (pre != null) {
pre.left = null;
pre.right = curr;
}
// === 关键逻辑 ===
// 因为栈是"后进先出" (LIFO),
// 我们希望遍历顺序是:中 -> 左 -> 右。
// 所以必须【先压入右子节点】,【再压入左子节点】。
// 这样下一轮循环 pop() 的时候,才能先拿到左子节点。
if (curr.right != null) {
stack.push(curr.right); // 先入栈(后出)
}
if (curr.left != null) {
stack.push(curr.left); // 后入栈(先出)
}
// 更新 pre,准备处理下一个节点
pre = curr;
}
}
}题解3(前置节点,时间On,空间O1)
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void flatten(TreeNode root) {
TreeNode cur = root;
// 开启遍历,直到处理完所有节点
while (cur != null) {
// 只有当左子树存在时,才需要进行"搬运"和"拼接"操作
// 如果左子树为空,说明左边已经没有东西了,直接往右走即可
if (cur.left != null) {
// 提前保存左子节点,因为后面它会变成新的 cur.right
TreeNode next = cur.left;
// === 步骤 1: 寻找前驱节点 (Predecessor) ===
// 目标:找到左子树中"最右边"的节点。
// 原因:在前序遍历中,这个节点是左子树最后被访问的节点,
// 原本的右子树 (cur.right) 应该接在这个节点的后面。
TreeNode predecessor = cur.left;
while (predecessor.right != null) {
predecessor = predecessor.right;
}
// === 步骤 2: 嫁接 (Rewiring) ===
// 将当前节点原本的右子树,接到前驱节点的右边
// 此时结构变为:cur -> left ... -> predecessor -> (原 cur.right)
predecessor.right = cur.right;
// === 步骤 3: 移动左子树 ===
// 将原本的左子树,整个搬移到当前节点的右边
// 这一步实现了:cur -> (原 left) -> ... -> predecessor -> (原 cur.right)
cur.right = next;
// === 步骤 4: 清理左指针 ===
// 必须将左指针置空,符合"单链表"结构(只有 right 指针)
cur.left = null;
}
// === 步骤 5: 继续下一个节点 ===
// 因为刚才已经把左子树移到了右边,所以这里 cur.right 就是原来的左子节点(现在的下一个处理对象)
cur = cur.right;
}
}
}思路
这道题如果使用递归的话很简单,就是创建一个链表存储先序遍历的节点,然后之后重新组装即可,但是会破坏树的结构,如果要求不破坏树的结构呢?就需要使用迭代的先序遍历,并且设置一个pre来临时存储。但这两个方法都是空间On的,如何做到空间O1呢,就需要使用前置节点,但力扣官网的该方法讲解有错误,所以需要简单修改一下,具体描述为
"...该节点的左子树中最后一个被访问的节点,是左子树中的最右边的节点。
在前序遍历的顺序中,这个节点(左子树最右节点)恰好是'当前节点的右子节点'的前驱节点。
因此,为了保证前序遍历顺序的连贯性,我们需要把'当前节点的右子树'接到'左子树最右节点'的后面。"
简单说,我们可以找到当前节点右子树的前置节点,因此就可以把当前节点的右子树直接挪到前置节点的右结点处。具体操作如下:
对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束