引言
随着基于冯·诺依曼架构的数据传输瓶颈日益凸显,存内计算(In-MemoryComputing, CIM)成为突破能效墙的关键技术。其中,阻变存储器(RRAM)凭借其非易失性和易于高密度集成的特性,成为实现CIM的一种理想载体。RRAM阵列不仅支持基于流或IMPLY/MAGIC逻辑门的操作,而且由于RRAM逻辑单元的物理结构与2:1多路选择器具有高度同构性,二元决策图(BDD)便成为了RRAM逻辑综合的首选表达形式。
本文将沿着逻辑综合的演进,探讨如何将抽象的BDD布尔逻辑转化为物理电路:Shirinzadeh等人[1]在算法层面解决了BDD多目标参数的搜索优化;Chakraborty等人[2]通过3x3切片架构与MAGIC逻辑提升了物理映射的效率与鲁棒性;Hassen等人[3]引入FreeBDD,通过打破逻辑数据结构中的全局顺序限制,实现高压缩比的阵列合成。
第一章:基于NSGA-II的BDD多目标优化
在逻辑综合的第一阶段,论文的任务非常明确:在数据结构(ROBDD)保持不变的前提下,通过寻找最佳的"变量排序",挖掘出电路性能的极限。这本质上是一个在巨大搜索空间中寻找最优解的数学问题。
1.1 问题的数学化:重新定义"代价"
传统的BDD优化通常只看"节点总数",认为节点越少越好。但在RRAM电路设计中,为了适配RRAM的物理特性,需要重新定义两个核心代价函数:
- 面积代价(Cost_Area):在RRAM电路中,我们通常采用并行评估策略,这意味着决定最终芯片面积的不是所有节点的总和,而是最宽那一层的节点数量(如图1)

图1 RRAM逻辑电路综合的代价函数参数定义与计算公式
- 延迟代价(Cost_Delay):由于采用并行计算,信号穿过一整层的时间是固定的。电路的延迟主要取决于BDD的层数,而不是节点的多少。
1.2 解决方案:NSGA-II(非支配排序遗传算法)
面积和延迟往往是冲突的。试图减少层数可能会导致某一层的节点爆炸性增长。传统的单目标搜索算法无法处理这种矛盾。
为此,该研究引入了NSGA-II算法,其核心机制如下:
- 将变量排序转化为多目标博弈:算法将BDD的变量顺序(如A->B->C或C->A->B)编码为"染色体"。通过模拟生物进化的交叉和变异,在保持变量序列合法的前提下,不断生成新的排序方案。
- 寻找"非支配解":算法不再寻找唯一的最优解,而是寻找帕累托前沿。这一组解的特点是:在它们之中,无法找到一个方案在面积和延迟上都同时优于另一个方案。这给了设计者极大的自由度:是想要极致的速度还是极致的面积,都可以根据需求从这组解中选择。图2展示了直观理解这种优化策略的效果。在该案例中,算法发现了一个反直觉的现象:初始BDD虽然节点数较少(6个),但因为存在跨层的非连续扇出(FO=1),导致RRAM消耗较高。而优化后的BDD(图2(b))虽然节点数增加到了8个,但通过消除了FO,反而实现了RRAM总数(从12降至11)和计算步数的双重下降。这完美印证了该算法在处理复杂物理代价冲突时的有效性。
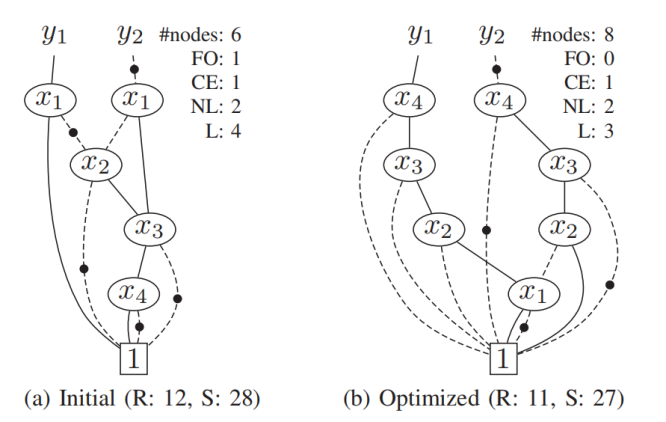
图2 优化前后的BDD结构对比
通过NSGA-II算法,我们在标准ROBDD的框架下找到了这一组"非支配解"。然而, ROBDD严格的"固定变量顺序"限制了逻辑压缩的潜力。目前的优化还停留在图论层面,并没有解决如何将这些逻辑节点高效地映射到真实的、存在物理干扰的RRAM阵列中。
第二章:切片架构与MAGIC逻辑的高效映射
在确定二进制决策图(BDD)为布尔函数的核心表征结构后,下一步就是将其高效映射到阻变存储器(RRAM)交叉阵列的物理层面。本章基于2020年发表于《IETComputers&DigitalTechniques》的研究成果,聚焦器件与物理实现的适配性,提出切片式交叉阵列架构与MAGIC逻辑映射方法。
2.1传统全阵列映射的物理局限
传统BDD映射方案采用大规模单片交叉阵列,目前仍存在一些问题。首先是潜行路径(SneakPath)干扰问题,大规模阵列中未选中的忆阻器会形成寄生导通路径,导致逻辑状态读取错误,尤其在读取高阻态(逻辑0)时该现象更为显著。同时,大阵列中活跃器件的操作易改变非目标忆阻器的阻值状态,破坏存储数据完整性。为缓解这些问题,传统方案需施加额外的半选电压(Half-select)或隔离电压(VISO)保护非激活器件,但随着阵列规模扩大,隔离能耗呈指数级增长,会额外带来能耗开销。
2.2 3x3切片式交叉阵列架构 和MAGIC逻辑映射方法
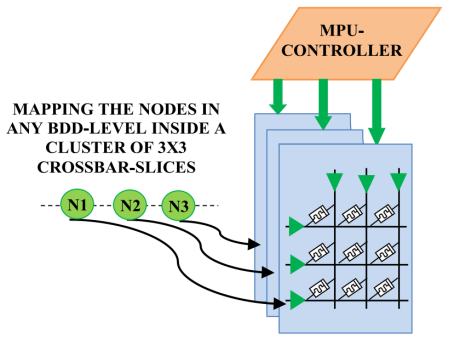
图3 BDD节点映射
针对全阵列的固有缺陷,该研究提出切片化(Slicing)映射策略,将BDD节点分散映射到一组3x3尺寸的小规模交叉阵列切片(Crossbar-Slices)中。如图3所示,每个切片独立承载一个BDD节点的逻辑功能(即一个2:1多路选择器MUX),通过多切片级联构成完整的逻辑计算单元。这种小尺寸3x3的紧凑结构大幅缩短了电流路径,从物理层面抑制了潜行路径的形成。小规模阵列中需要隔离的非激活忆阻器数量显著减少,使得隔离能耗降低至全阵列方案的几分之一。
为进一步提升映射效率,研究采用MAGIC(MemristorAidedLogic)设计风格,相比传统IMPLY逻辑,其无需额外电阻硬件,且具有非破坏性读出的优势。在具体实现上,该方案设计了优化的2:1MUX门级电路,仅需3个2输入NOR门和1个NOT门,相比传统设计减少了NOT门的使用数量。该方案同时提出6步高效映射流程(Step-Count=6),如图4所示,在3x3切片中完成逻辑运算。关键点在于利用切片内空闲忆阻器直接存储中间变量(如S的反变量S′),避免了传统方案中额外的NOT操作步骤,使得映射速度较传统MAGIC方案(7步)和IMPLY方案(11步)得到提升。考虑到控制忆阻器状态转换,确保逻辑运算的正确性,每一步操作中仍需要对特定行列施加执行电压(VEXE)、隔离电压(VISO)等信号。
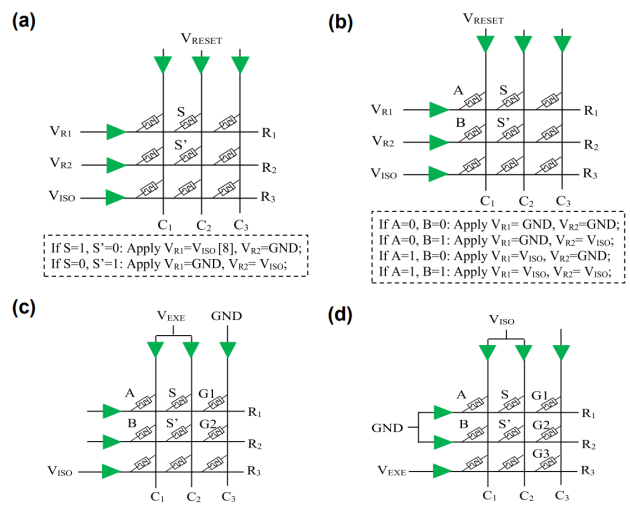
图4基于MAGIC的映射
切片式架构与优化MAGIC映射的结合,实现了忆阻计算物理层的性能突破:实验结果表明,该方案相比传统切片架构,逻辑运算速度平均提升27%,忆阻器使用数量平均减少42%。然而,该方案仍基于简化有序二进制决策图(ROBDD)结构,未能解决复杂逻辑函数(如乘法器、大型算术单元)中BDD节点数量指数级增长的根本问题。
第三章: 基于FreeBDD的存算一体忆阻器阵列设计自动化研究
如何将复杂的布尔函数高效地映射至忆阻器交叉阵列(Crossbar),一直是EDA(电子设计自动化)领域的难题。传统方法多基于受限的逻辑表达模型,导致硬件面积冗余。AmadUlHassen等人提出了一种创新思路:打破逻辑数据结构中的全局顺序限制,利用自由二分决策图(FreeBDD, FBDD)实现高压缩比的阵列合成。
3.1 ROBDD
在数字逻辑合成领域,简化有序二分决策图(ReducedOrderedBDD, ROBDD)作为一种经典的数据结构,因其正则性(Canonicity)而备受青睐。ROBDD全局变量顺序固定,这意味着在从根节点到终点节点的任何路径上,变量出现的先后顺序必须一致。这种刚性约束虽然简化了逻辑等价性检查,但在面向忆阻器阵列映射时,固定的全局顺序会导致某些计算路径上出现大量冗余的中间节点。这些节点在映射至物理忆阻器阵列时直接转化为额外的纳米线和交叉点,限制了阵列的压缩率,并增加了寄生路径(Sneak-path)管理的复杂度。如果底层数据结构本身存在局限性,单纯依靠参数优化(如遗传算法优化变量顺序)往往会陷入局部最优。
3.2 FreeBDD (FBDD)
Hassen等人的研究是FBDD,其核心概念在于:彻底放宽全局变量顺序的约束,允许在同一函数表达中,不同路径上的变量顺序互不相同。这赋予了FBDD逻辑表达极高的灵活性。在FBDD中,针对不同的输入向量空间,可以选择最利于当前分支压缩的变量先分解。这使得FBDD在表达某些特定函数(如乘法器中间位)时,其节点总数能够呈多项式级缓慢增长,而非ROBDD常见的指数级增长。
在物理映射层面,这种逻辑上的自由对应了阵列布线的优化。忆阻器交叉阵列本质上是一个双标图(BipartiteGraph)物理载体。如图5所示,通过去除冗余边,研究者能够显著减少建立sneak-path所需的忆阻器数量,从而在物理层面上实现更小的芯片面积。
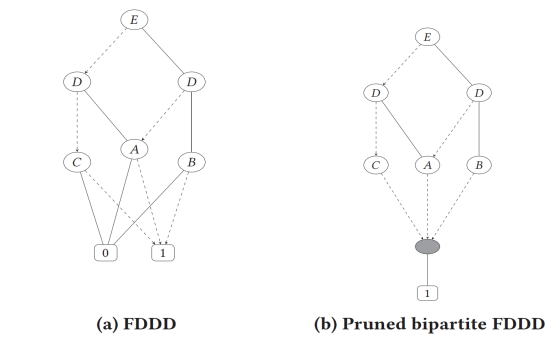
图5 FBDD 去除与终端节点"0"相连的冗余边缘
3.3 基于子电路规模的局部启发式算法
失去全局顺序的指引后,如何构建一个接近最优的FBDD成为了新的挑战。由于不再有统一的顺序,合成算法必须在每个节点的分裂点上进行"即时决策"。
本文提出的基于"电路表示规模(Circuit-representationSize)"的局部启发式合成策略,核心逻辑在于对每一个节点进行Shannon展开时,算法不但检查变量出现的频率,而且预估分裂后生成的两个子函数(Co-factors)的电路复杂度。具体而言,算法通过计算子函数在DNF(析取范式)下的AND/OR门总数来量化规模,这种动态选择策略使得FBDD在构建过程中能够沿各个路径自适应地寻找局部最优解,从而在整体结构上达到极高的紧凑度。
结语
CIM逻辑综合经历了从局部改良到结构革新的逐步演进,这标志着后摩尔时代的集成电路设计已转向算法、架构与数据结构的协同设计(Co-design)。未来的EDA工具必须具备跨层级的优化能力:既要深谙物理器件的微观特性(如MAGIC操作),又要具备宏观数据结构的动态重构能力(如FBDD),通过全栈式创新突破存算一体化的性能瓶颈。
- Shirinzadeh,S.,Soeken,M.,&Drechsler,R.(2016,April).Multi-objectiveBDDoptimizationforRRAMbasedcircuitdesign.In2016IEEE19thInternationalSymposiumonDesignandDiagnosticsofElectronicCircuits&Systems(DDECS) (pp.1-6).IEEE.
- Chakraborty,A.,Maurya,V.,Prasad,S.,Gupta,S.,Chakraborty,R.S.,&Rahaman,H.(2021).Binarydecisiondiagram‐basedsynthesistechniqueforimprovedmappingofBooleanfunctionsinsidememristivecrossbar‐slices.IETComputers&DigitalTechniques ,15 (2),112-124.
- UlHassen,A.,Khokhar,S.A.,Butt,H.A.,&Jha,S.K.(2018,July).Freebddbasedcadofcompactmemristorcrossbarsforin-memorycomputing.InProceedingsofthe14thIEEE/ACMInternationalSymposiumonNanoscaleArchitectures (pp.107-113).