一、原始观测值方程
1.1 基本伪距观测方程

1.3 包含系统误差改正的观测方程

二、观测方程的线性化
由于几何距离 \rho_iρi 与接收机坐标是非线性关系,必须进行线性化才能求解。
2.1 泰勒展开


2.2 方向余弦计算



2.3 线性化观测方程


三、定位方程构建与求解
3.1 矩阵形式

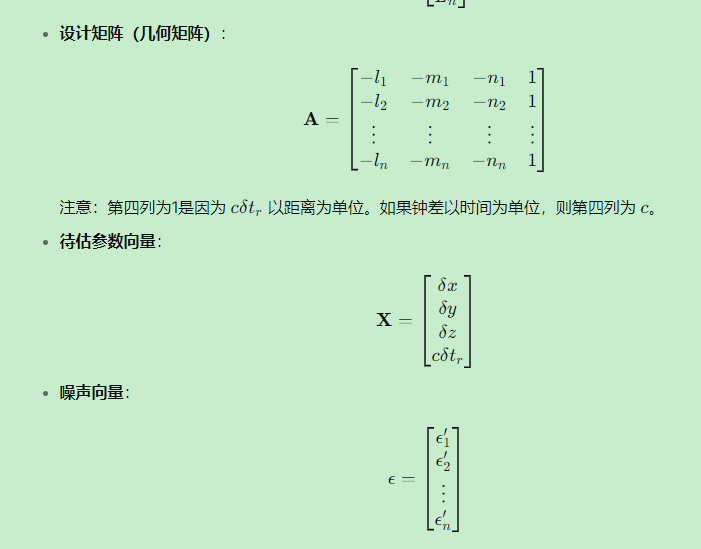
伪距观测方程的向量方式推导
现在一般的穿戴设备都是使用的单点定位。从观测方程到定位方程的公式如下。大概过程是将卫星到接收机的真实距离通过向量线性化,化为卫星到接收机概率位置的向量加速概率位置到真实距离的偏差向量的和。


该方程是GNSS单点定位、差分定位和精密单点定位(PPP)的基础。在实际应用中,通过迭代求解线性方程组,不断更新近似位置,直到改正数收敛为止。
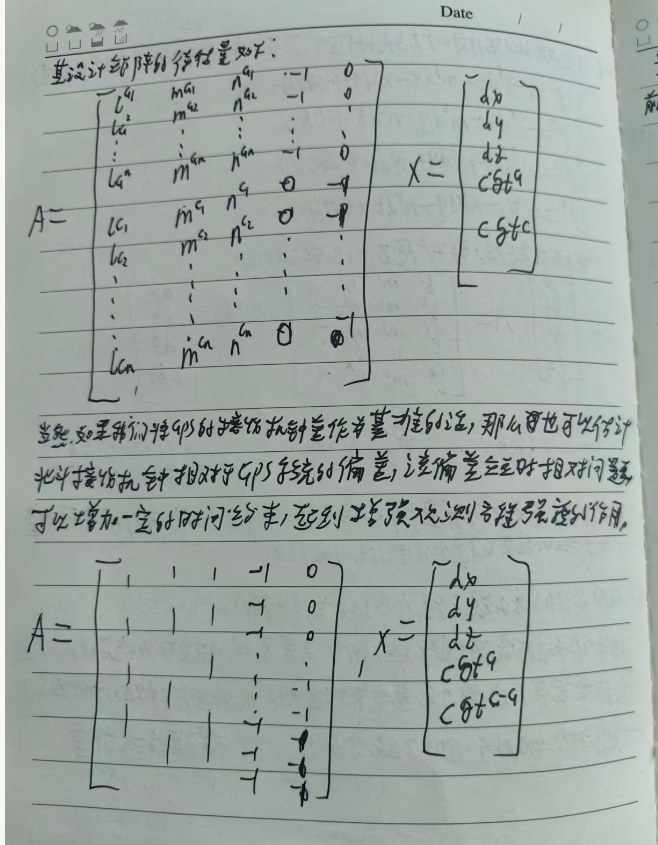
多系统定位方程,因为GPS和BDS是两个系统,所以主要表现在接收机端的误差会存在差异,这些误差会被接收机钟进行吸收,所以我们一般可以为GPS和BDS系统分别估计一个个接收机钟差。
接收机钟估计的是接收机晶振也就是接收机本地的时间和GNSS时间框架的差异。由于多系统定位时,各个卫星定位系统对于本地接收机钟来说是一个晶振,所以可以先以GPS为基准接收机钟偏差,然后BDS
系统可以在GPS接收机钟偏差的基础上再估计一个偏差,这个偏差就是很稳定了,和接收机晶振无关,可以对这个稳定量进行建模,这相当于间接多了一个观测量。因为卫星系统的时间是比较稳定的,所以两个卫星系统的时间偏差也是很稳定的。
下面是高等数学里面空间解析几何关于向量的简单介绍笔记




