day150—数组—二叉树的锯齿形层序遍历（LeetCode-103）

题目描述

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

复制代码

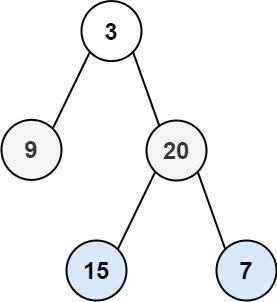
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

复制代码

输入：root = [1]
输出：[[1]]

示例 3：

复制代码

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

解决方案：

这段代码的核心功能是实现二叉树的锯齿形层序遍历（之字形遍历） （即第一层从左到右，第二层从右到左，第三层再从左到右，以此类推交替遍历），在普通层序遍历的基础上增加了 "偶数层反转结果" 的逻辑，时间复杂度 O(n)（n 为节点数），空间复杂度 O(n)，是该问题的经典迭代解法。

核心逻辑

代码在普通层序遍历（双数组模拟 BFS）的基础上，通过一个布尔标记控制 "是否反转当前层节点值数组"，实现锯齿形效果：

边界处理：若根节点为空，直接返回空数组；
初始化容器与标记 ：
- 保留普通层序遍历的 ans（最终结果）、cur（当前层节点）、nxt（下一层节点）、value（当前层节点值）；
- 新增布尔变量 even（初始为 false），标记当前层是否为 "需要反转的偶数层"（第一层不反转，第二层反转，以此类推）；
逐层遍历循环 ：
- 与普通层序遍历一致：遍历当前层节点，收集值到 value，并按左→右顺序收集下一层节点到 nxt；
- 核心新增逻辑：若 even 为 true（当前是偶数层），调用 reverse 反转 value 数组，实现从右到左的遍历效果；
- 将处理后的 value 加入 ans，更新 cur 为下一层节点，并翻转 even 的值（切换下一层的遍历方向）；
返回结果 ：遍历完成后，ans 中按锯齿形存储了各层节点值，直接返回即可。

总结

核心思路：在普通层序遍历的基础上，通过布尔标记 + 数组反转实现锯齿形，无需改变节点遍历顺序，仅调整结果数组的顺序，逻辑简洁；
关键细节：even 初始为 false（第一层不反转），每遍历完一层就翻转 even，保证奇偶层交替反转；
效率特点：整体时间 O(n)（反转操作的总时间为 O(n)，所有节点仅遍历一次），空间开销与普通层序遍历一致，是最优解法之一。

函数源码：

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
        if(!root)   return {};
        vector<vector<int>>ans={};
        vector<TreeNode*>cur={root};
        vector<TreeNode*>nxt={};
        vector<int>value={};
        bool even=false;
        while(!cur.empty()){
            value={};
            nxt={};
            for(auto i:cur){
                value.push_back(i->val);
                if(i->left) nxt.push_back(i->left);
                if(i->right)nxt.push_back(i->right);                
            }
            if(even) reverse(value.begin(),value.end());
            ans.push_back(value);
            cur=nxt;
            even=!even;
        }
        return ans;
    }
};