视觉矩阵之 正交矩阵

一、定义

正交矩阵 是一个特殊的方阵 （行数和列数相等）。它的核心定义是：
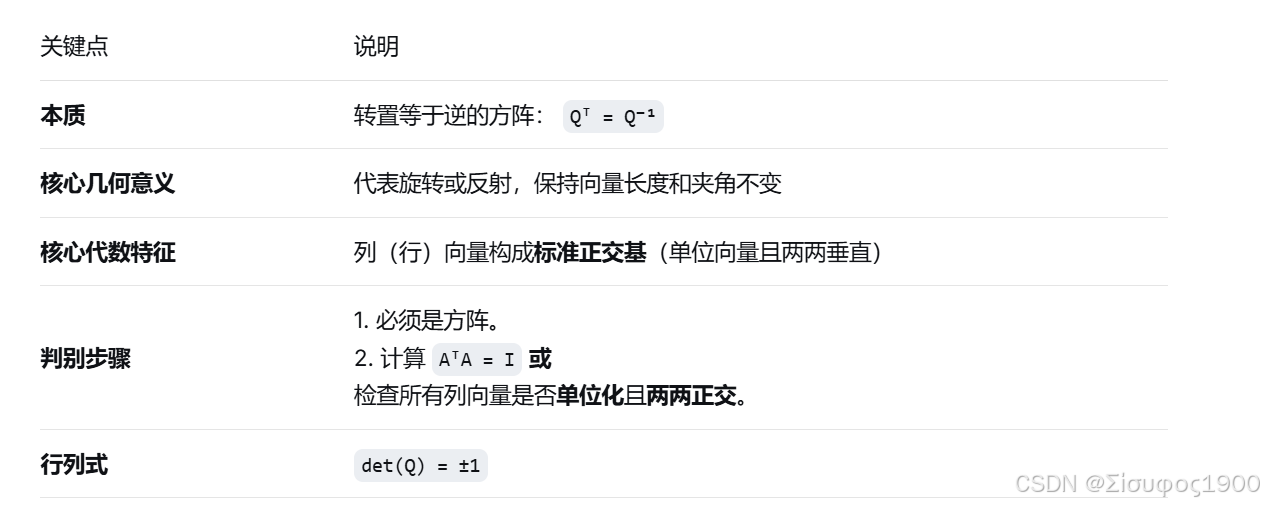
一个矩阵 Q 的转置 Qᵀ 等于它的逆矩阵 Q⁻¹。

二、几何意义和性质

几何特点：

可以把正交矩阵想象成一种**"刚性变换"** 的数学表示。它作用于空间中的向量时，就像旋转 或者镜像反射一样，能保持向量的"形状"和"结构"不变。

具体来说，Q 是正交矩阵，意味着：

1. 保持长度不变 ：

   对于任何向量 x，有 ||Qx|| = ||x||。将一个向量旋转或反射，它的长度不会变。

2. 保持夹角（内积）不变 ：

   对于任何两个向量 x 和 y，有 (Qx)·(Qy) = x·y。这意味着两个向量之间的角度在经过变换后保持不变。

   • 推论 ：正交向量变换后依然是正交的。

3. 列（或行）构成标准正交基 ：

   这是判别和构造正交矩阵的关键。

   • 列视角 ：把矩阵 Q 写成列向量的形式 Q = [q₁, q₂, ..., qₙ]。那么这些列向量 qᵢ 满足：

     • 单位长度 ： ||qᵢ|| = 1 （每个列向量的长度都是1）

     • 两两正交 ： qᵢ · qⱼ = 0 （当 i ≠ j 时）

       这样的向量组称为 标准正交向量组。它们是n维空间中的一组"标准尺子"。

   • 行视角：正交矩阵的行向量同样构成一组标准正交基。

代数特点：

1. 行列式的值只能是 1 或 -1：

   • det(Q) = 1： 对应的是纯旋转（保持坐标系的手性，比如左手系还是左手系）。

   • det(Q) = -1： 对应的是旋转加镜像反射（改变了手性，比如把左手系变成了右手系）。

2. 可逆且逆很好求 ：

   由于 Q⁻¹ = Qᵀ，求它的逆矩阵非常简单，只需要转置即可，计算量极小。

3. 乘积保持正交性 ：
   如果 Q 和 P 都是正交矩阵，那么它们的乘积 QP 也是正交矩阵。连续进行旋转/反射，结果还是一个旋转/反射。

三、 如何判别一个矩阵是否正交？

根据定义和特点，有几种等价的判别方法。对于一个给定的方阵 A，你可以：

方法1：使用定义（最根本）

计算 AᵀA，看结果是否等于单位矩阵 I。

• 计算 AᵀA。

• 检查 结果矩阵的对角线元素是否都是 1，非对角线元素是否都是 0。

• 如果 AᵀA = I，那么 A 就是正交矩阵。

注意 ：对于方阵，AᵀA = I 会自动推出 AAᵀ = I，所以检查一个即可。

方法2：检查列向量（最常用、最直观）

将矩阵 A 的每一列看作一个列向量 c₁, c₂, ..., cₙ。

• 条件1： 检查每个列向量的长度（模）是否为 1。

  • 即，对于每个 cᵢ，计算 cᵢ · cᵢ（或各分量平方和），结果应为 1。

• 条件2： 检查任意两个不同的列向量是否正交（点积为0）。

  • 即，对于所有 i ≠ j，计算 cᵢ · cⱼ = 0。

• 如果所有列向量都是单位向量 且两两正交 ，那么 A 就是正交矩阵。

方法3：检查行向量

与方法2完全类似，检查所有行向量是否构成标准正交基。

方法4：结合行列式（辅助判断）

先看 A 是否是方阵，然后计算 det(A)。如果 det(A) 不是 ±1，那它肯定不是 正交矩阵。如果是 ±1，则需要再用方法1或2确认（因为仅凭行列式为±1不足以判定正交）。

案例1

以最经典的 2维旋转矩阵 为例：

方法2：检查列向量

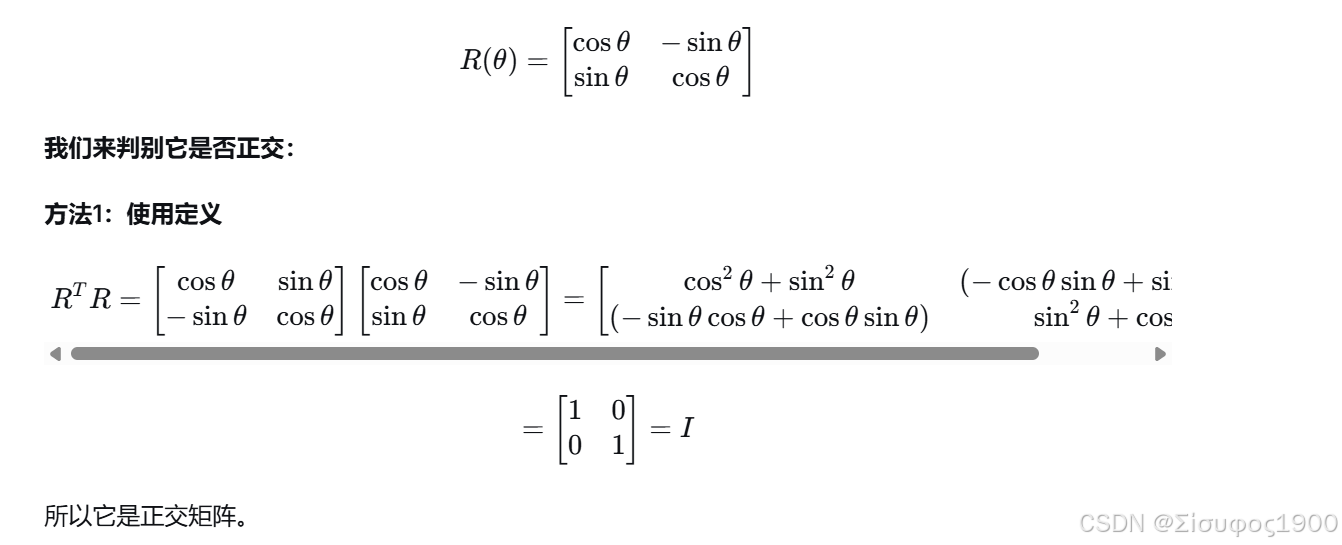
方法2：检查列向量

• 列1： c₁ = [cosθ, sinθ]ᵀ

  • 长度： √(cos²θ + sin²θ) = √1 = 1

• 列2： c₂ = [-sinθ, cosθ]ᵀ

  • 长度： √((-sinθ)² + cos²θ) = √(sin²θ + cos²θ) = 1

• 两列点积： (cosθ)*(-sinθ) + (sinθ)*(cosθ) = 0

• 所有条件满足，所以它是正交矩阵。

几何意义 ：这个矩阵 R(θ) 正是将平面内的向量绕原点逆时针旋转 θ 角度的变换，它完美地保持了向量的长度和夹角。

四、总结：

正交矩阵就是一个"不拉伸、不压缩、只旋转或镜像"的变换，它的列向量就像一把互相垂直的、长度为1的标准尺子。