前言
本系列文章承接C++基础的学习,需要++有C语言的基础++ 才能学会哦~
第18篇主要讲的是有关于C++的**++二叉搜索树基础++** 。
C++才起步,都很简单!!
目录
二叉搜索树
具有以下性质的二叉树:
① 若左子树不为空,则左子树上所有结点****≤**根结点的值。
② 若右子树不为空,则右子树上所有结点****≥**根结点的值。
③ 它的左右子树也分别为二叉搜索树。
称之为二叉搜索树。++特别的,空树也是二叉搜索树++。
也可以反过来,右 ≤ 根 ≤ 左。
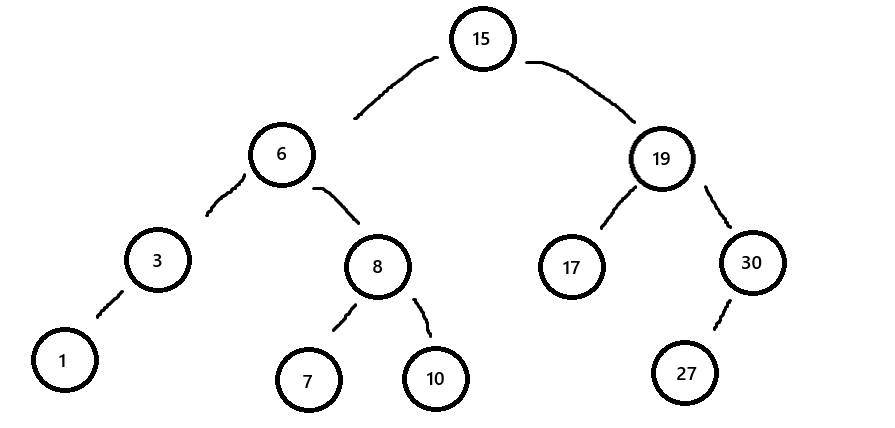
图1
二叉搜索树,又叫二叉排序树。
当我们将二叉搜素树++中序(左根右)输出后,为升序数列++ 。
上图中序输出为:1,3,6,7,8,10,15,17,19,27,30。
那么顾名思义,这种结构的作用就是++Ⅰ.便于搜索++ ,++Ⅱ.便于排序++。
根据二叉搜索树的性质,我们在查找结点的时候++最多只需要查找n次,n为树的层数++,搜索速度很快。
性能分析
如图,结点大小和上图完全相同,但是排列情况不同,层数更大,但也是二叉搜索树。
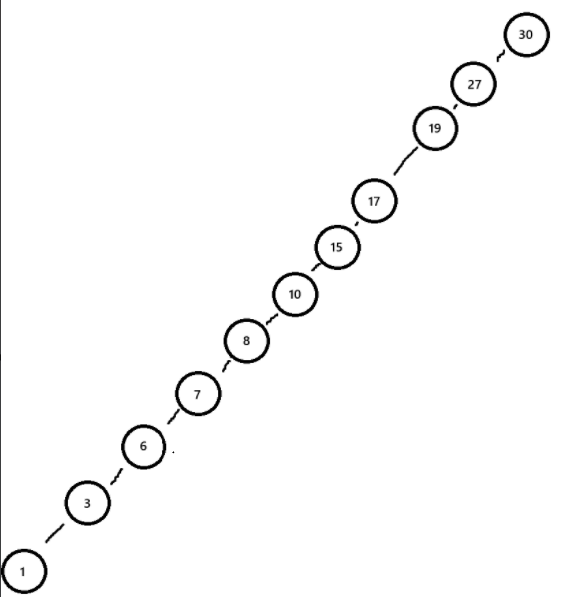
图2
这时的搜索,最多就要搜索11层,比原来多了7层!++这说明二叉搜索树排列不同,搜索性能是不同的,波动很大++,因此,我们实际上使用更多的是平衡二叉搜索树(如图1),这个后面再学,先按下不表。
二叉搜索树的增删查改
cpp
template<class K>
struct BSTNode
{
K _key;
BSTNode<K>* _right;
BSTNode<K>* _left;
BSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};二叉搜索树结点结构代码
插入
① 如果++树为空++ ,则直接新增结点,赋值给root指针。
② 如果++树不为空++ ,++按照二叉搜索树性质++,++大往右,小往左,找空插++ 。插入值比当前结点大就往右走,插入值比当前结点小就往左走,找到空位插入新结点。
③ ++插入相等的值时,可以往右也可以往左,但是要注意保持一致性++,要么都往右要么都往左。有相同的值,称为冗余,我们一般默认不存相同的数值。
但是如果进行了旋转子树的操作,那么即使插入时统一了,实际存储也不一定就是预料的那样。
cpp
boll Insert(const K& key)//默认不支持冗余
{
if (_root == nullptr)
{
_roor = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}查询
无冗余查找:
cpp
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}存在冗余查找:
比如要求找到重复对象中的中序输出的第一个。
在上述代码的基础上,查找到相等数值的节点后不返回,继续在左子树中找目标对象,找到了再输出true
代码略······
删除
首先查找结点,在树中再进行删除。
情况①: 删除的是叶子结点。
解决方法:++直接释放删除++。
情况②: 删除的结点只有一个孩子。
解决方法:让++父结点的孩子指针指向孩子的孩子++,然后再删除释放中间结点
情况③: 删除的结点有两个孩子。
解决方法:用++右子树的最小结点++ or++左子树的最大结点替代该结点++,替代完成后,再删除释放中间结点。
因为++空树也能算是二叉搜索树++,所以我们可以把++叶子结点当作是有两个孩子且都为空树的结点++,++并且并到情况②中进行处理++。
cpp
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
//先查找对象
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
//找到对象,准备删除
else
{
//情况一和二合并以情况二的方法处理,
if(cur->_left == nullptr)
{
//删除根结点的特殊情况处理
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_right)
{
parent->_right = cur->_right;
}
else
{
parent->left = cur->left;
}
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
//删除根结点的特殊情况处理
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (cur == parent->_right)
{
parent->_right = cur->_left;
}
else
{
parent->_left = cur->_left;
}
}
delete cur;
return true;
}
//情况三
else
{
//找右子树最小结点替代
Node* minRight = cur->_right;
Node* minRightParent = cur;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
//进入了while循环
if (minRightParent->left == minRight)
{
minRightParent->_left = minRight->_right;
}
//未进入while循环
else
{
minRightParent->_right = minRight->_right;
}
return true;
delete minRight;
}
}
}
return false;
}修改
**二叉搜索树的关键码(作为排列根据的数值key)不可修改。**否则可能会破坏二叉搜索树的规则。
修改操作只能修改关键值和父母孩子指针之外的成员变量,所以实际修改时,就是先查找再自定义修改可修改的值,没什么特别的。
二叉搜索树的key和key/value的搜索场景
key搜索场景
只有key作为关键码时进行的搜索。
此时,结构中只存储key就好了,key为用来排列二叉搜索树的依据。这种场景下的搜索场景支持增删查,但是不可以改,理由可见上文"修改"部分。
**生活中使用场景:**业主开车进小区停车场,扫描车牌,以车牌为关键码搜索该车牌是否为本小区车辆。
key/value搜索场景
每一个key关键码都有与之对应的值value,value可为任意对象。
此时,除了key,还要存储value。增删查依旧用key按照二叉搜索树的规则进行搜索,然后可以根据key找到对应的value。key不可修改,但是value可以。
**生活中使用场景:**简单中英文互译字典,可英文作key,中文作value;商城车库,以车牌号为key,车辆入场后value记录为入场时间,出场之后,以车牌号key查找到对应的入场时间,然后再用出场时间减去value的入场时间,得出停车时间,接着计算出停车费用,value修改为停车费用。
❤~~本文完结!!感谢观看!!接下来更精彩!!欢迎来我博客做客~~❤