0.理论基础
参考:
分类:
1、满二叉树:
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
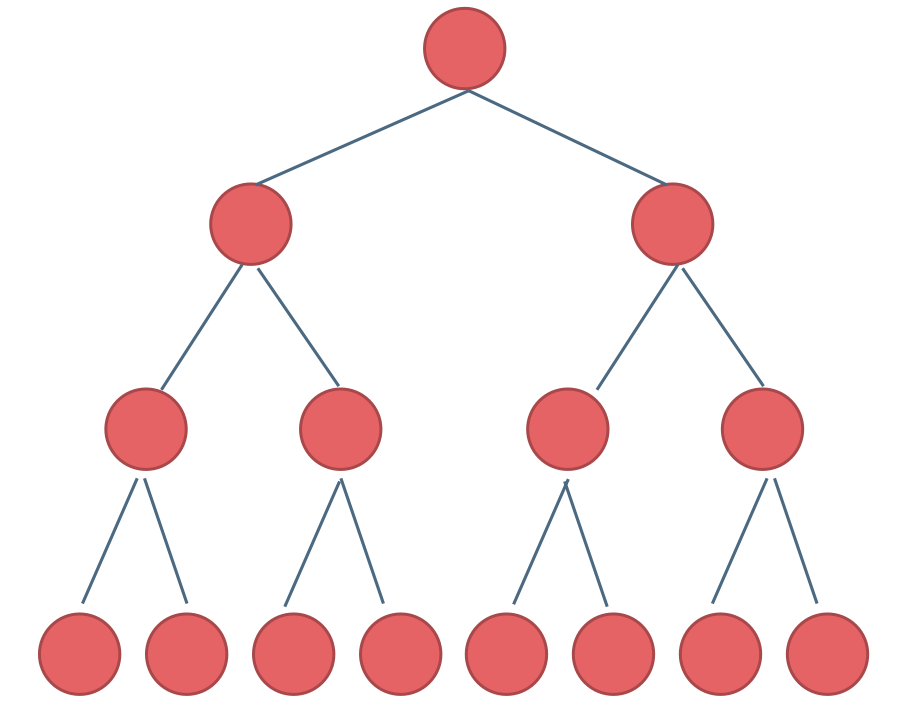
2、完全二叉树:
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
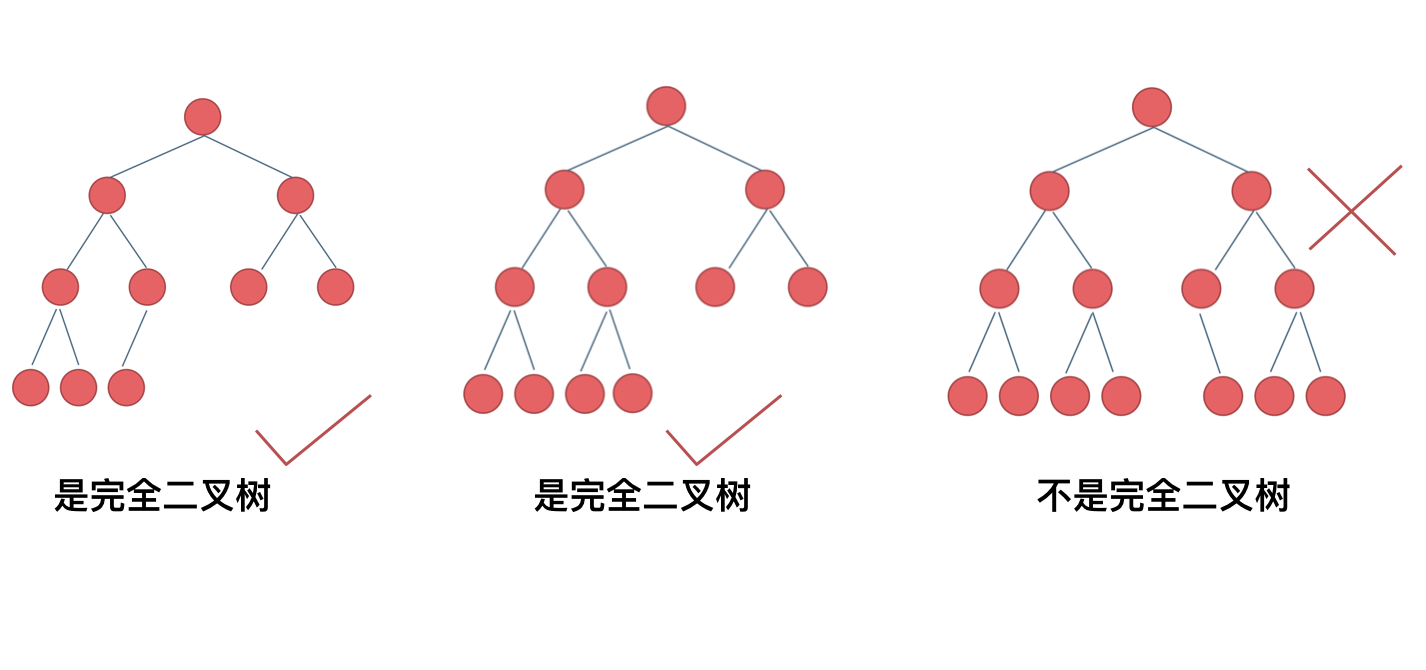
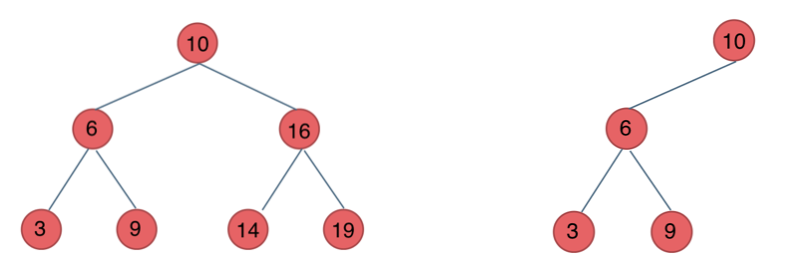
3、二叉搜索树:
有数值且有序
- 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 它的左、右子树也分别为二叉排序树
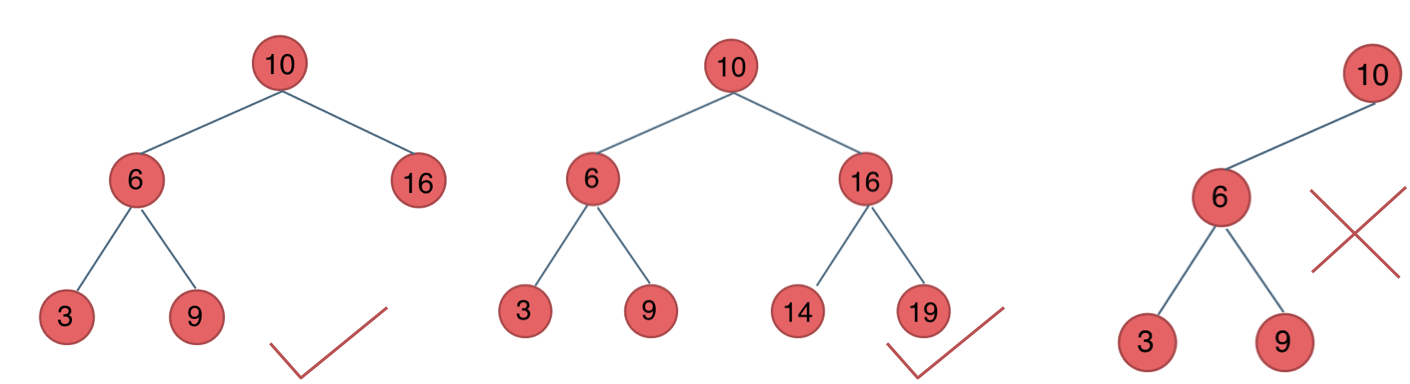
4、平衡二叉搜索树:
又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
遍历方式:
1、深度优先遍历:
先往深走,遇到叶子节点再往回走。
前中后序指中间节点的遍历顺序
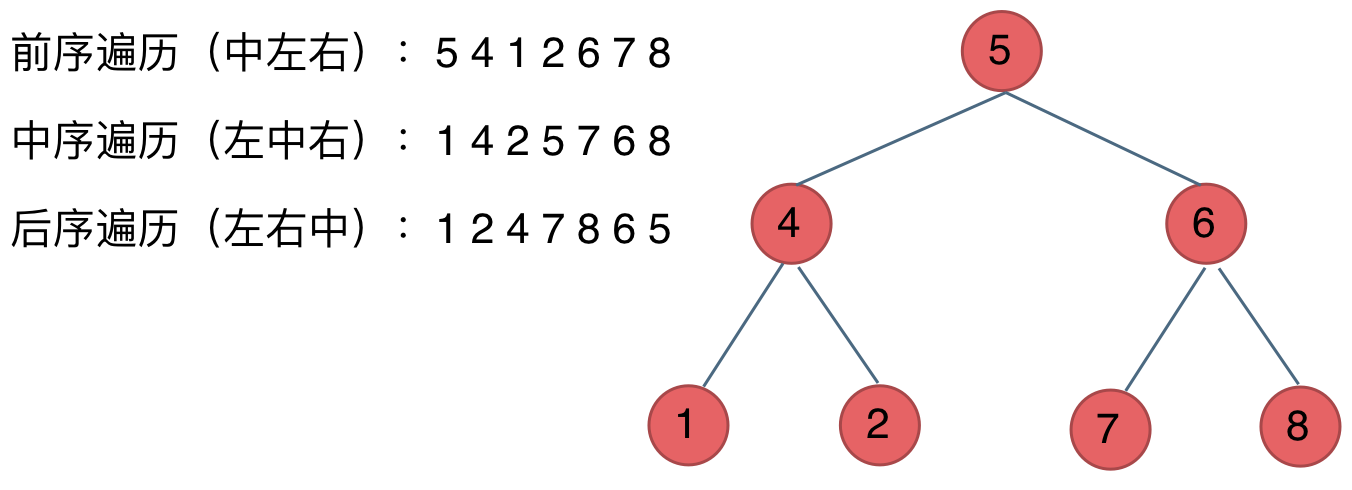
- 前序遍历------中左右(递归法,迭代法)
- 中序遍历------左中右(递归法,迭代法)
- 后序遍历------左右中(递归法,迭代法)
2、广度优先遍历:
逐层遍历
94.二叉树的中序遍历
一、递归
三部曲:
1、确定递归函数的参数和返回值:传入节点
2、确定终止条件:遍历节点为空直接返回
3、确定单层循环逻辑:中序遍历为左中右,按顺序循环,取中间节点数值
代码:
python
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
res = []
def dfs(node):
if node is None:
return
dfs(node.left) # 递归左子树
res.append(node.val) # 中间节点加入结果数组
dfs(node.right) # 递归右子树
dfs(root)
return res二、迭代
思路:
用栈存储,需要时取出顶部元素。由于是中序遍历,首先迭代访问左子树,遍历到最左节点后取出栈顶元素加入结果数组,然后向栈顶元素的右子树进行遍历。
代码:
python
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
# 为空的情况
if root is None:
return []
# 创建一个栈,先存储节点,便于回溯
stack = []
res = []
cur = root
# 需要两个
while cur or stack:
# 栈非空且当前节点非空
if cur:
# 向左遍历并存储(按中间、左节点的顺序存的,取出就为先取左节点再取的中间)
stack.append(cur)
cur = cur.left
else: # 栈非空但当前节点为空
# 取出左边/中间的节点存入结果数组,再向右遍历
cur = stack.pop()
res.append(cur.val)
cur = cur.right
return res104.二叉树的最大深度
一、层序遍历
参考:
讲透二叉树的层序遍历 | 广度优先搜索 | LeetCode:102.二叉树的层序遍历_哔哩哔哩_bilibili
思路:
使用队列,用一个变量记录该层元素个数,以知道后续要从队列中弹出的元素个数;遍历每一层时需要将对应元素的子节点加入到队列当中
代码:
python
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
# 记录深度,创建列表
depth = 0
queue = collections.deque([root])
while queue:
depth += 1
size = len(queue) # 记录每一层的节点数
# 按层来取出节点,加入下一层节点
for _ in range(size):
cur = queue.popleft()
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
return depth二、递归
三部曲:
1、确定参数及返回值:参数为节点,返回值为高度
2、确定终止条件:遍历节点为空返回0
3、确定单层循环逻辑:一定要是后序遍历左右中,因为只有把两个子树先遍历完了才能够对左子树和右子树高度进行比较,否则无法比较
代码:
python
class Solution:
def getDepth(self, node):
if not node:
return 0
leftHeight = self.getDepth(node.left)
rightHeight = self.getDepth(node.right)
height = 1 + max(leftHeight, rightHeight)
return height
def maxDepth(self, root: Optional[TreeNode]) -> int:
return self.getDepth(root)226.反转二叉树
思路:
先交换左右节点,然后再递归处理左子树右子树
代码:
python
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root is None:
return root
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root复杂度分析:
- 时间复杂度:O(n),其中 n 为二叉树的节点个数。
- 空间复杂度:O(n)。最坏情况下,二叉树退化成一条链,递归需要 O(n) 的栈空间。
101.对称二叉树
一、递归
思路:
递归处理二叉树的外侧节点和内侧节点,分别对比对应节点是否相同;把特殊情况单列出来返回,包括:对应节点一个为空一个非空、都非空、值不相等的情况,此时可以直接返回,若两个值相等了,就可以继续递归
代码:
python
class Solution:
def compare(self, left, right):
# 把左右节点的各种情况单独列出
if left is None and right:
return False
elif right is None and left:
return False
elif right is None and left is None:
return True
elif left.val != right.val:
return False
# 分别遍历二叉树的外侧节点和内侧节点,来判断是否都相同
outside = self.compare(left.left, right.right)
inside = self.compare(left.right, right.left)
isSame = outside and inside
return isSame
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if root is None:
return True
return self.compare(root.left, root.right)复杂度分析:
- 时间复杂度:O(n),其中 n 为二叉树的节点个数。
- 空间复杂度:O(n)。最坏情况下,二叉树退化成一条链,递归需要 O(n) 的栈空间。
二、迭代
思路:
和层序遍历有点像,用队列来成对记录左右节点,方便对比
代码:
python
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if root is None:
return True
queue = collections.deque([root.left, root.right]) # 要传入左右节点
while queue:
leftNode = queue.popleft()
rightNode = queue.popleft()
# 两节点都为空
if not leftNode and not rightNode:
continue
# 两节点有一个不为空或者值不相等
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
# 先传入外侧两节点,再传入内测两节点,方便两两对比
queue.append(leftNode.left)
queue.append(rightNode.right)
queue.append(leftNode.right)
queue.append(rightNode.left)
return True