进阶篇-3-数学篇-2--从线性代数到AI：向量、矩阵、张量的底层逻辑

从线性代数到AI：向量、矩阵、张量的底层逻辑

作者：Weisian

上一篇，我们探讨了数学在人工智能中的"灵魂地位"。今天，让我们步入这座数学宫殿的第一厅------线性代数。

想象一下，你第一次拼乐高积木。

摆在你面前有一堆五颜六色的小方块------有的长、有的扁、有的带圆角。一开始觉得它们看起来杂乱无章；但当你学会把它们按形状、颜色和方向组合起来的时候，就能搭出房子、飞船，甚至整个城市。

人工智能的世界，其实也像一场超级复杂的乐高游戏。而向量、矩阵、张量 ，就是它的基础积木。

眼睛在哪儿？鼻子多高？嘴巴多宽？------这些看似模糊的"样子"，在AI眼里，全是一串串数字；而把这些数字组织起来、让它们"说话"的语言，就是线性代数。

在线性代数的世界里，万物皆可被结构化、量化、计算。而人工智能，正是建立在这套语言之上的智能工程。

如果说AI是一辆高速行驶的智能汽车，那么：

• 数据是燃油，
• 算法是发动机，
• 线性代数就是底盘与传动系统------没有它，再强大的引擎也无法驱动现实。

今天，我将用最生活化的方式，带你理解向量、矩阵、张量这些"数学积木"，以及它们如何层层构建起AI的宏伟殿堂。

---

一、为什么AI离不开线性代数？------它是最高效的"数据语言"

AI的核心任务，是从数据中学习规律，并做出预测或决策。

但计算机无法直接理解图片、文字或语音------它只认得数字。

于是，我们必须把现实世界的一切，翻译成一组可计算、可比较、可操作的数字结构 。

线性代数，正是这套"翻译系统"和"运算框架"。

🌰 举个例子：AI如何识别一张猫的照片？

1. 转数字：将图片拆解为像素，每个像素的亮度/颜色变成一个数字；
2. 结构化：把这些数字组织成向量（单图）或张量（彩色图）；
3. 提特征：通过矩阵运算，提取"有耳朵""胡须对称""毛色橘黄"等模式；
4. 做判断：将结果与"猫"的标准向量比对，输出识别结论。

整个过程，每一步都依赖线性代数提供的表示能力 与计算能力。

✅ 一句话总结 ：
线性代数 = AI的"数据骨架" 。

没有它，AI看到的世界只是一堆杂乱无章的数字；有了它，AI才能"看懂"结构、发现规律、做出智能响应。

更具体地说，线性代数在AI中承担三大核心角色：

1. 数据表示：将非结构化数据（图、文、音）转化为向量、矩阵、张量；
2. 特征提取：通过投影、变换、降维等操作，筛选关键信息；
3. 模型运算：神经网络的前向传播、反向传播，本质都是线性代数运算。

接下来，我们逐层拆解这三大"积木"------向量、矩阵、张量。

---

二、向量：AI世界的"最小数据单元"

2.1 什么是向量？------一组有序的"特征清单"

在传统数学中，向量是"既有大小又有方向的量"。

但在AI语境下，我们可以更直观地理解为：一个对象的数字化身份证------由一组有序数字组成，每个数字代表一个属性。

🌰 生活化类比：

• 一杯奶茶 → [甜度3, 温度60℃, 价格18元, 热量350大卡]
• 一个人 → [年龄28, 身高175, 体重65, 月薪15k]
• 一句话 → [词1编码, 词2编码, ..., 词n编码]

这里每一行的数据，就是一个向量。它们不包含主观描述，却完整刻画了对象的客观特征。

💡 在AI中，向量通常以列向量形式存在（竖着排），便于后续与矩阵相乘。

---

2.2 向量在AI中的三大核心作用

（1）表示单个数据对象：AI的"通用语言"

所有AI要处理的数据，必须先转换为向量，才能进入计算流程。这是AI理解世界的起点。

• 图像领域 ：

  一张 28×28 的手写数字图，共 784 个像素。AI将其展平为一个 784 维向量：

  [120, 200, 255, ..., 30, 10, 0]

  每个数字代表对应位置的灰度值（0=黑，255=白）。

  

  ✅ 关键理解 ：向量不是"图像本身"，而是其数字化骨架。

• 自然语言领域 ：

  每个词被映射到高维空间中的一个点。例如使用 Word2Vec 或 BERT 后：

  • "猫" → [0.8, -0.3, 1.2, ..., 0.5]（128维）
  • "狗" → [0.75, -0.25, 1.1, ..., 0.48]
  • "汽车" → [-0.6, 0.9, -0.4, ..., -0.7]

  可见，"猫"与"狗"的向量数值接近，而与"汽车"相差甚远。

  💡 生活类比 ：就像地图坐标------北京和天津离得近，北京和乌鲁木齐离得远。

  向量空间就是AI的"语义地图"，距离 = 语义相似度。

• 推荐系统领域 ：

  用户行为被汇总为偏好向量。例如平台定义三个兴趣维度：美食、穿搭、科技，你的向量可能是：

  [0.85, 0.3, 0.65]

  • 第1位 0.85：高度关注美食；
  • 第2位 0.3：很少看穿搭；
  • 第3位 0.65：偶尔浏览科技。

  这个向量就是AI为你定制推荐的依据------它不关心你是谁，只关心你的"数字画像"长什么样。

---

（2）计算数据间的相似度：AI的"比较逻辑"

当所有对象都变成向量后，AI判断"是否相似"，就转化为计算两个向量的距离或夹角。

• 例子1：推荐系统的精准匹配

  • 用户A向量：[0.8, 0.2, 0.5]
  • 商品B（零食）向量：[0.9, 0.1, 0.1] → 距离近 → 优先推荐
  • 商品C（T恤）向量：[0.1, 0.9, 0.1] → 距离远 → 不推荐
    此外，若用户E的向量与A高度相似（都喜欢美食），系统会把E买过的零食推荐给A------这就是"猜你喜欢"的核心逻辑。

• 例子2：图像识别的对号入座

  上传一张猫图 → 转为784维向量 → 与数据库中"猫""狗""车"的标准向量比对：

  • 与"猫"距离：0.3
  • 与"狗"距离：1.2
  • 与"车"距离：2.5
    → 距离最近的是"猫"，AI判定为猫。

• 常用计算方式：两种"测距工具"各有侧重

  • 欧氏距离 ：计算两点间直线距离，适用于数值大小直接反映差异的场景（如像素值、消费金额）。
    公式简化：√(x₁−y₁)² + (x₂−y₂)² + ...
  • 余弦相似度 ：忽略向量长度，只看方向是否一致，更适合语义、偏好等场景。
    • 用户A [0.8,0.2,0.5] 与用户E [0.7,0.3,0.4] 方向一致 → 相似度高；
    • "猫"与"汽车"方向迥异 → 相似度接近0。

---

（3）特征组合与变换：从基础到高级

AI还能通过向量运算，将多个基础特征组合成高级语义 。

例如识别猫时：

• 先提取"边缘""色块"等低级向量；
• 再通过加权求和、非线性激活，得到"耳朵形状""胡须轮廓"等高级特征向量；
• 最终完成整体识别。

这正是深度学习"层次化特征学习"的起点。

---

三、矩阵：AI处理批量数据的"高效工具"

3.1 什么是矩阵？------向量的集合，数据的表格

矩阵，就是由多个向量组成的二维数组，可理解为"批量数据清单"。

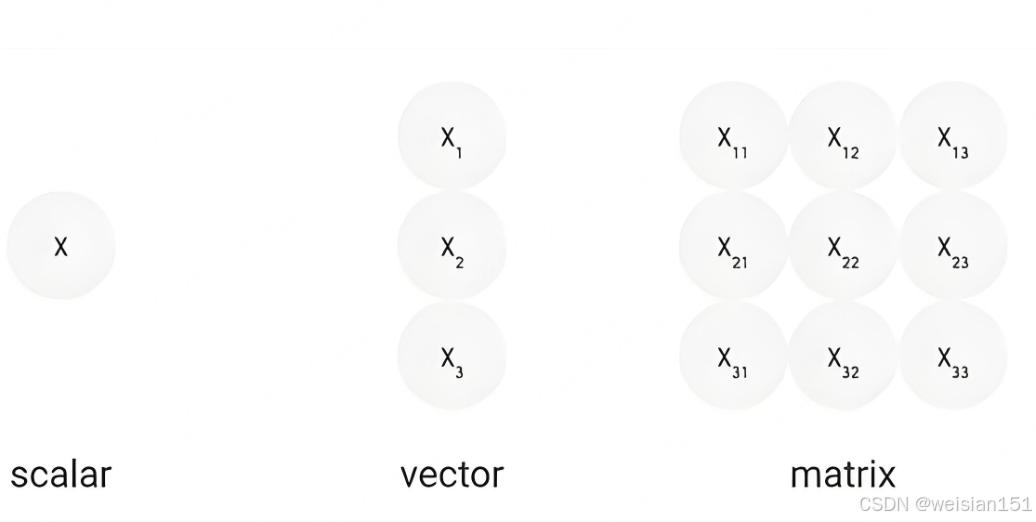
🌰 生活化类比：

• 奶茶店订单表：

甜度	温度	价格	热量
3	60	18	350
5	50	20	400
0	70	16	300

每一行是一个奶茶的向量，整体是一个 3×4 矩阵。

在AI中，矩阵通常表示为 样本数 × 特征数 。

例如：1000张手写数字图 → 1000×784 矩阵（1000个样本，每个784维）。

---

3.2 矩阵在AI中的四大核心作用

（1）表示批量数据：特征矩阵

AI训练时，整个数据集就是一个特征矩阵：

• 行 = 样本（一张图、一个用户、一段语音）
• 列 = 特征（像素值、点击率、频率分量）

此外，还有权重矩阵，存储模型学到的参数，用于后续运算。

---

（2）数据预处理：批量标准化与降维

AI对数据的清洗和优化，本质是对矩阵的列进行统一运算：

• 标准化：让每列均值为0、标准差为1，避免"价格"这类大数值掩盖"甜度"等小数值的影响；
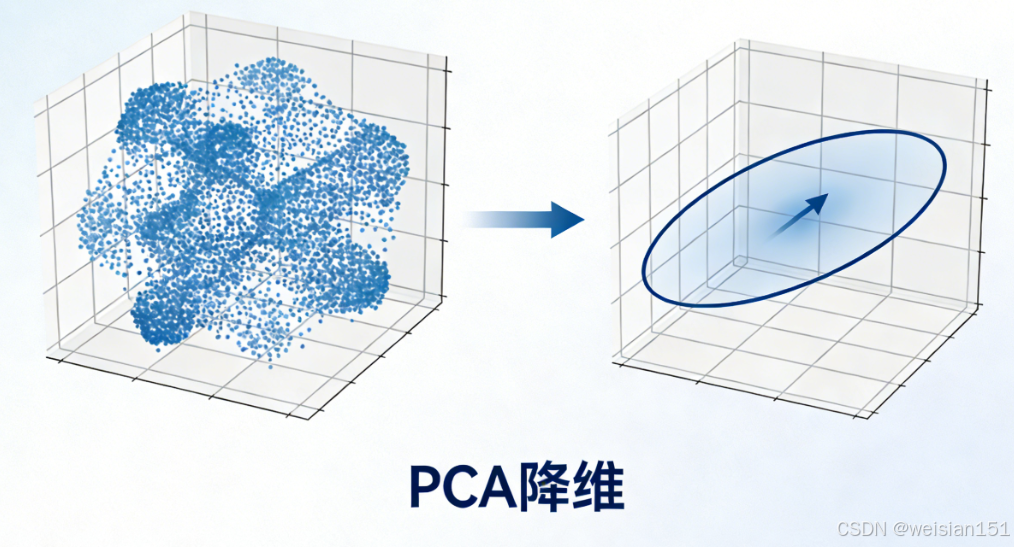
• 降维（如PCA）：通过矩阵乘法，将高维特征（784维）压缩到2D/3D，便于可视化或加速训练。

⚡ 优势 ：一行矩阵运算，即可处理成千上万个样本、数百个特征，效率远超循环逐个处理。

---

（3）神经网络的核心运算：矩阵乘法驱动智能

神经网络的每一层，本质都是：

输出 = 输入矩阵 × 权重矩阵 + 偏置向量

举例：

• 输入：1000张图 → 1000×784 矩阵
• 第一层权重：784×128 矩阵（学习128个隐藏特征）
• 输出：1000×128 矩阵（每个样本的新表示）

🔥 关键洞察 ：

GPU之所以能加速AI训练，正是因为其擅长并行执行大规模矩阵乘法。

---

（4）求解线性方程组：模型训练的数学本质

AI模型的训练，本质上是寻找最优权重矩阵 ，使得预测结果最接近真实标签。

这一过程涉及大量线性方程组的求解，而矩阵的逆、行列式、特征值等工具，正是解决这些问题的基石。

---

四、张量：AI处理高维数据的"终极形态"

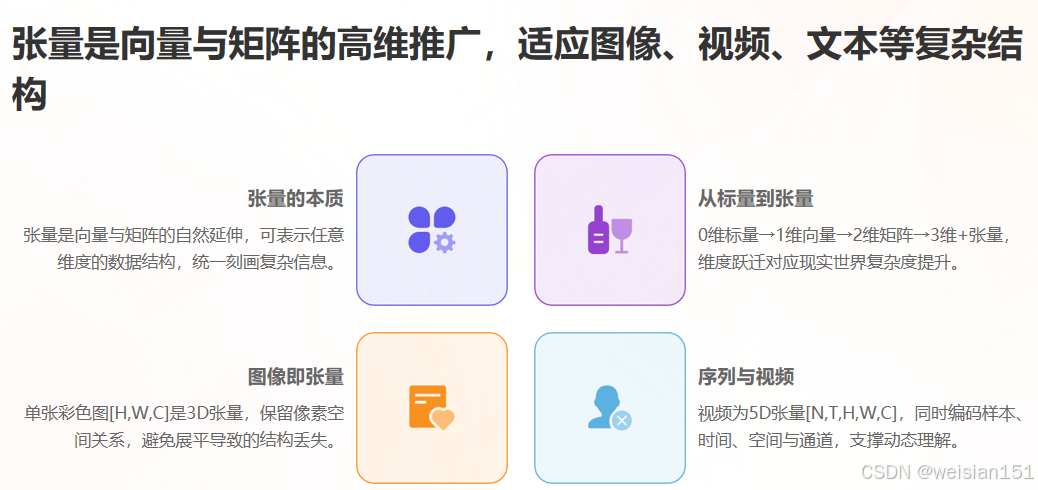
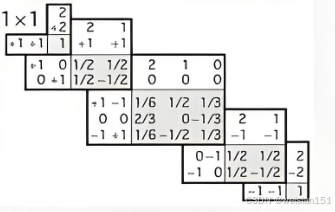
4.1 什么是张量？------矩阵的高维扩展

张量是向量和矩阵的自然推广：

• 0维张量：标量（单个数字，如价格18元）
• 1维张量 ：向量（如 [3,60,18,350]）
• 2维张量：矩阵（如订单表）
• 3维及以上：高维张量（如"数据立方体"）

🌰 生活化类比：

• 3维张量 ：奶茶店3天的订单 → [天数, 订单数, 特征数] = 3×100×4
• 4维张量 ：一段视频 → [帧数, 高, 宽, 通道数] = 24×28×28×3

在AI中，张量的维度称为"轴（Axis）"，不同轴代表不同语义。

---

4.2 张量在AI中的三大核心作用

（1）表示高维结构化数据

现实中的AI数据，大多是高维的：

• 计算机视觉：

  • 单张彩色图 → [H, W, C]（如 224×224×3）
  • 一批图片 → [N, H, W, C]（N=样本数）
  • 视频 → [N, T, H, W, C]（T=时间帧）

• 自然语言处理：

  • 一篇文章 → [句子数, 词数, 词向量维]
  • 一批文章 → [批次, 句子, 词, 128]

• 语音处理：

  • 音频频谱 → [时间步, 频率维]，批量处理时为3维张量

✅ 关键优势 ：张量保留了数据的原始结构（如图像的空间邻接性、文本的时序性），而矩阵展开会破坏这种结构。

---

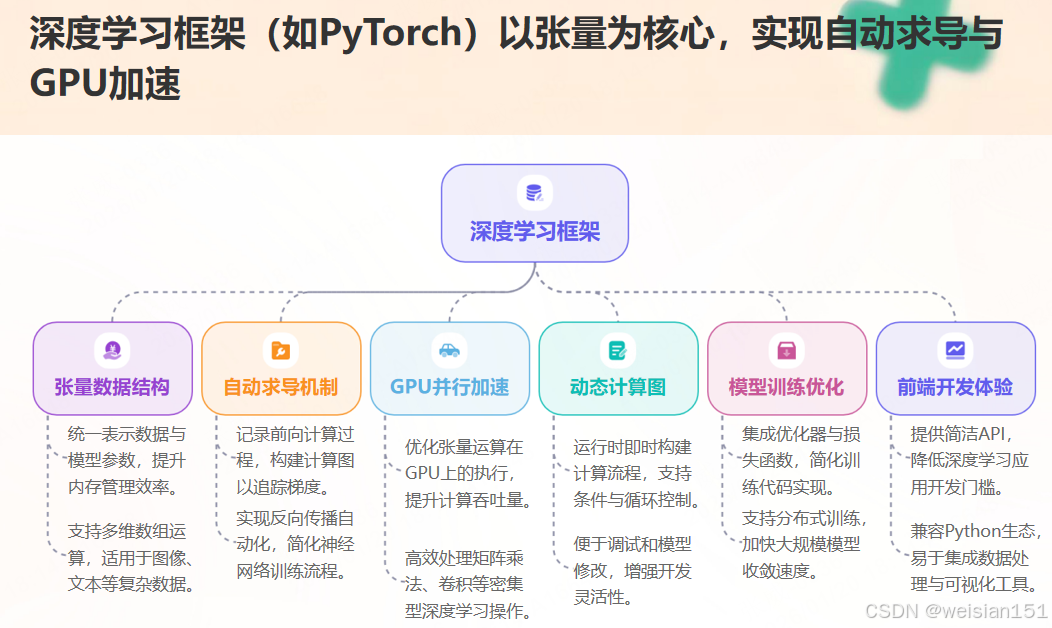
（2）适配深度学习框架的运算

主流框架（TensorFlow、PyTorch）的核心数据结构就是张量 。

开发者只需定义张量形状和运算，框架自动完成：

• 并行计算
• 自动求导（反向传播）
• GPU加速

举例 ：

输入一批图片 [32, 3, 224, 224] → 经过卷积层 → 输出 [32, 10]（32个样本的10类概率）

全程无需手动循环，全部由张量运算完成。

---

（3）高维特征的提取与融合

张量支持多维度并行特征提取：

• CNN 对图像张量做卷积 → 提取空间特征（边缘、纹理）
• RNN 对文本张量做递归 → 提取时序特征（语法、逻辑）
• Transformer 对注意力张量做加权 → 提取全局依赖

这使得AI能同时理解数据的局部与整体、静态与动态。

---

五、三剑客的协同逻辑：从数据到智能的完整闭环

向量、矩阵、张量并非孤立存在，而是层层递进、协同工作，构成AI数据处理的完整链路：

1. 输入阶段：

   • 单对象 → 向量（1D张量）
   • 批量数据 → 矩阵（2D张量）
   • 高维数据（图、视频、文本）→ 高维张量（3D+）

2. 预处理阶段 ：

   通过矩阵/张量运算（标准化、裁剪、增强），清洗并优化数据。

3. 模型运算阶段：

   • 全连接层：矩阵乘法
   • 卷积层：张量卷积
   • 注意力机制：高维张量加权
     逐层提取从低级到高级的特征。

4. 输出阶段 ：

   最终张量（如10维概率向量）被解读为人类可理解的结果（"这是数字3"）。

🔄 闭环总结 ：
向量是AI的"词汇" ------ 让一切可量化；
矩阵是AI的"语法" ------ 定义批量关系与变换；
张量是AI的"篇章" ------ 组织复杂高维信息。

---

六、从理论到实践：手写数字识别的线性代数之旅

让我们用 MNIST 手写数字识别 串起所有概念：

步骤1：数据准备（向量化）

每张 28×28 图片 → 展平为 784维向量

[像素1, 像素2, ..., 像素784]

步骤2：批处理（矩阵化）

一次处理100张 → 100×784 矩阵

[[图1的784像素],
 [图2的784像素],
 ...
 [图100的784像素]]

步骤3：神经网络层（矩阵乘法）

第一层：784维 → 256维隐藏层

权重W: 784×256（待学习参数）  
偏置b: 256维  
输出 = 输入矩阵 × W + b

步骤4：多通道特征（张量化）

在卷积层中：

• 输入：[100, 28, 28, 1]（灰度图）
• 卷积核：[3, 3, 1, 32]（32个3×3滤波器）
• 输出：[100, 26, 26, 32]（32个特征图）

步骤5：最终决策（向量到标量）

输出10维概率向量：

[0.01, 0.01, 0.02, 0.90, ..., 0.01] → 识别为"3"

---

七、线性代数的现代扩展：应对真实世界的挑战

7.1 稀疏矩阵：处理大规模数据的"轻量化策略"

问题 ：推荐系统中用户-物品矩阵可能有数十亿元素 ，但99%是零（未交互）。
解决方案：仅存储非零元素及其位置。

• 传统存储：100万×100万 = 1万亿元素
• 稀疏存储：仅存约1000万非零项 → 压缩1000倍！

---

7.2 低秩近似：数据的"降维智慧"

核心思想 ：大多数数据可用少数"主成分"近似表示。
应用：

• 图像压缩（JPEG）
• 主题模型（从文档提取主题）
• 推荐系统（用户/物品的潜在因子）

---

7.3 特征分解与奇异值分解（SVD）：数据的"本质洞察"

比喻 ：将一道复杂菜肴分解为基本食材与烹饪方法。
AI应用：

• PCA（主成分分析）：数据降维
• 矩阵分解：Netflix推荐系统获奖方案
• LSA（潜在语义分析）：文本语义挖掘

---

八、写在最后：不必成为数学家，但要理解"骨架逻辑"

我知道，"向量""矩阵""张量"这些词容易让人紧张。

但请记住：你不需要手算特征值，也不用推导SVD公式。

作为AI使用者或开发者，你真正需要理解的是：

• 向量是AI的词汇------让一切可量化、可计算；
• 矩阵是AI的语法------定义数据间的关系和变换；
• 张量是AI的篇章------组织复杂的高维信息。

🌟 更深层的启示 ：

线性代数之所以成为AI的基石，是因为它提供了：

• 抽象能力：从具体问题中提炼数学结构；
• 计算框架：将智能问题转化为可计算的数值问题；
• 几何直觉：在高维空间中理解数据与模型。
  "我们不是在让计算机学习'思考'，而是在教它们如何'计算思考'。"

下一次，当你用面部解锁手机、收到精准推荐、或与聊天机器人对话时，请记得------

在这些智能体验的背后，是：

• 无数向量在高维空间中靠近，
• 无数矩阵在高速相乘，
• 无数张量在神经网络中层层流动。

线性代数，正在无声地编织着智能的网。

---

博主寄语 ：

数学不是AI的障碍，而是它的翅膀。

每一次你理解一个数学概念，都是在为AI这只巨鸟增添一根飞羽。

希望今天的分享，能让你在欣赏AI应用的同时，也能感受到背后数学之美。

记得点赞收藏，我们下期再见！

有任何问题或想法，欢迎在评论区留言讨论～ ✨