1、 该论文重新修订了E(S)公式,该公式指的是总数据消耗 E 与达到特定损失所需优化步骤数 S 之间的关系。原先的公式,如下图,并不适用于现在大模型预训练的方法(现在普遍采用WSD学习率调度器),关键批大小理论失效。
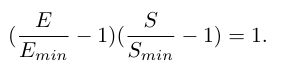
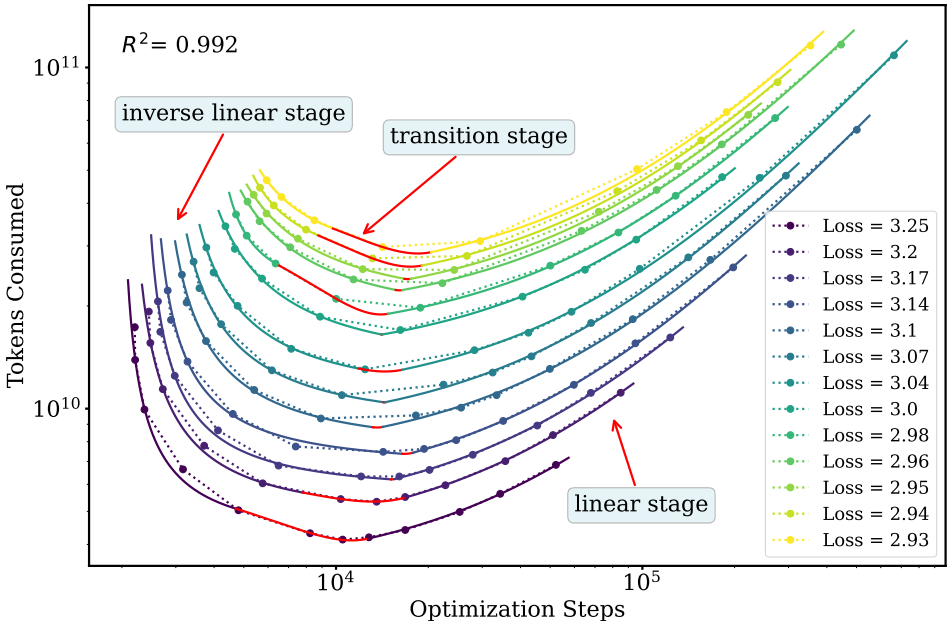
解决方案 :论文为WSD调度器推导了一个新的、分段形式的 E(S) 关系公式。该公式将训练过程分为三个阶段:初始阶段(E与S呈反比关系)、过渡阶段(E是S的二次函数)和渐近阶段(E与S呈线性关系)。实验表明,新公式能精确拟合WSD下的预训练动态。
2、基于新的E(S)框架,论文解释了WSD预训练的两个基本属性:
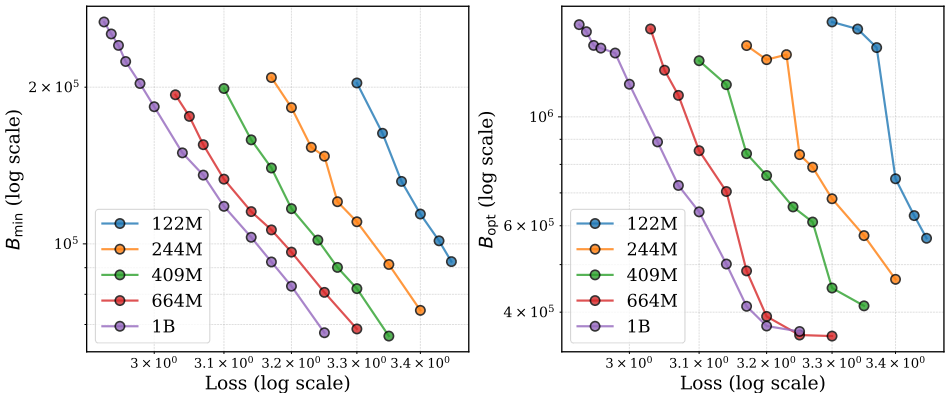
(1)达到目标损失所需的最小批量大小阈值Bmin:为了达到特定的目标损失,批大小必须超过的一个物理最小值。几何上,它等于E(S)曲线渐近线的斜率。
(2)通过最小化总token数来最大化数据效率的最优批量大小Bopt:使得达到目标损失所需的总数据消耗最小的批大小。几何上,它等于从原点到E(S)曲线最小值点连线的斜率。
论文进一步发现,随着训练损失降低(即训练进行),Bmin和Bopt都呈现单调递增的趋势。
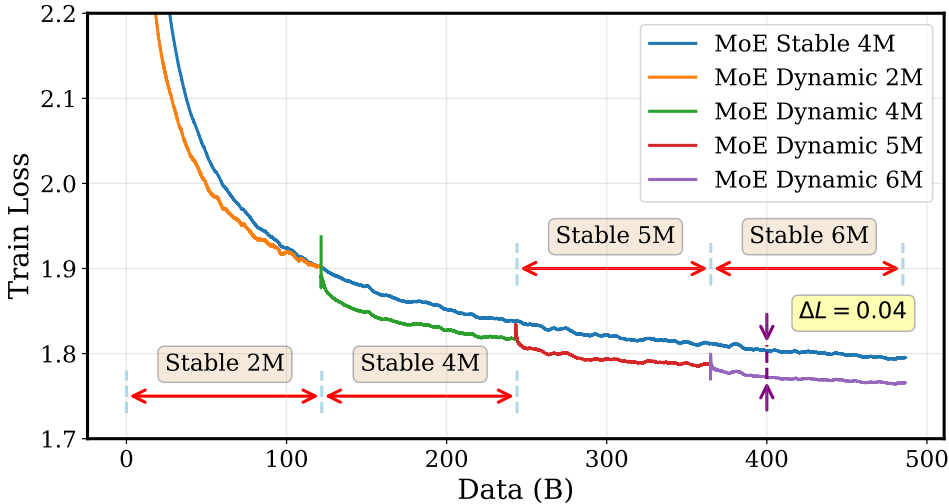
3、 鉴于Bopt随训练进程而增大的特性,在整个预训练过程中使用固定的批大小并非最优策略,提出了一种**动态batch size 调度器,**得到的策略能够显著提升训练效率和最终模型质量。
该策略根据训练已消耗的数据总量,分阶段地增加全局批大小(例如,在Qwen3模型的实验中,按照序列 {2M, 4M, 5M, 6M} 在每125B tokens后调整批大小)。
在Qwen3 Dense和MoE模型上的大量实验表明,与固定批大小基线相比,动态调度策略能获得更低的训练损失和更好的下游任务(MMLU, CMMLU)性能。
在related work里,作者提到了一个概念:scaling law 缩放定律
我特意去搜了这个词汇的意思:
缩放定律可以被视为大模型发展的"经验指南",是描述AI模型性能随模型规模、数据量或计算量增加而可以预测提升的统计规律。
神经缩放定律通常表现为三种形式:模型规模缩放,数据量缩放,计算量缩放。