PID算法改进
正对不同的使用场景,对PID调控进行相应改造。
积分限幅
限制积分的幅度,防止积分深度饱和
要解决的问题:如果执行器因为卡住、断电、损坏等原因不能消除误差,则误差积分会无限制加大,进而达到深度饱和状态,此时PID控制器会持续输出最大的调控力,即使后续执行器恢复正常,PID控制器在短时间内也会维持最大的调控力,直到误差积分从深度饱和状态退出
现象:KP0.3,KI0.2,Target20,控制输出轴不旋转可以看到输出值OUT会不断累加直到100,松开输出轴后电机以全速运行一段时间后才恢复到正常速度20,电机堵转时间越久,积分饱和就越深,后续松开输出轴电机从全速运转恢复到正常状态的时间就越久。当执行器断电,控制器还在运行时也会出现积分饱和的现象,如下图
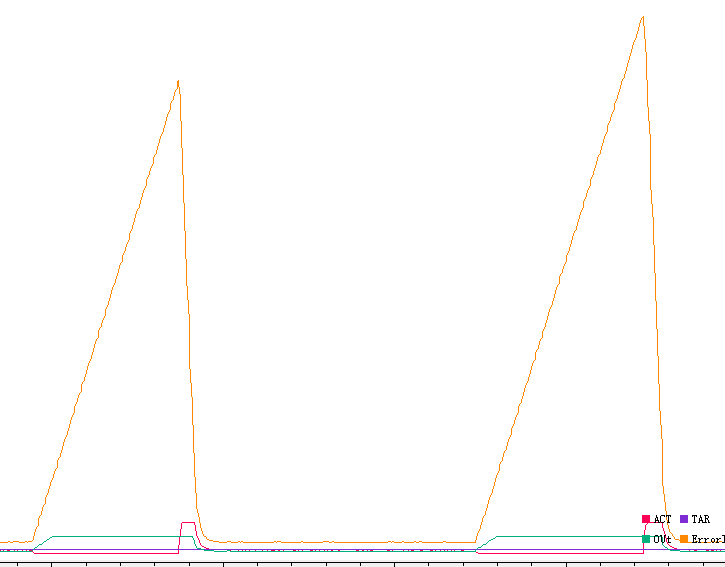
模拟代码:
c
float Target,Actual,Out;
float Kp=0,Ki=0,Kd=0;
float Error0,Error1,ErrorInt;
uint8_t motorFlag=0;
int main(void)
{
OLED_Init();
LED_Init();
Key_Init();
RP_Init();
Encoder_Init();
Motor_Init();
Timer_Init();
Serial_Init();
OLED_Printf(0,0,OLED_8X16,"Speed Control");
OLED_Update();
while (1)
{
if(Key_Check(KEY_1,KEY_SINGLE)){
motorFlag=!motorFlag;//使用按键模拟电机断电
}
if(motorFlag){
LED_ON();
}else{
LED_OFF();
}
Kp=RP_GetValue(1)/4095.0 *2;
Ki=RP_GetValue(2)/4095.0 *2;
Kd=RP_GetValue(3)/4095.0 *2;
Target=RP_GetValue(4)/4095.0*300 -150;
OLED_Printf(64,16,OLED_8X16,"Tar:%+04.0f",Target);
OLED_Printf(64,32,OLED_8X16,"Act:%+04.0f",Actual);
OLED_Printf(64,48,OLED_8X16,"OUT:%+04.0f",Out);
OLED_Printf(0,16,OLED_8X16,"Kp:%+4.2f",Kp);
OLED_Printf(0,32,OLED_8X16,"Ki:%+4.2f",Ki);
OLED_Printf(0,48,OLED_8X16,"Kd:%+4.2f",Kd);
OLED_Update();
Serial_Printf("%f,%f,%f,%f\r\n",Actual,Target,Out,ErrorInt);
}
}
void TIM1_UP_IRQHandler(){
static uint8_t count;
if(TIM_GetITStatus(TIM1,TIM_IT_Update)==SET){
count++;
if(count>=40){
count=0;
Actual=Encoder_Get();//获取当速度
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
if(Ki!=0){//防止积分饱和,导致系统暂时失去控制
ErrorInt+=Error0;
}else{
ErrorInt=0;
}
Out=Kp*Error0+Ki*ErrorInt+Kd*(Error0-Error1);//位置式PID计算输出
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}
if(motorFlag==1){
Motor_SetPWM(Out);//设置PWM
}else{
Motor_SetPWM(0);
}
}
Key_Tick();
TIM_ClearITPendingBit(TIM1,TIM_IT_Update);
}
}解决方法:对误差积分或积分项输出进行判断,如果幅值超过指定阈值,则进行限制
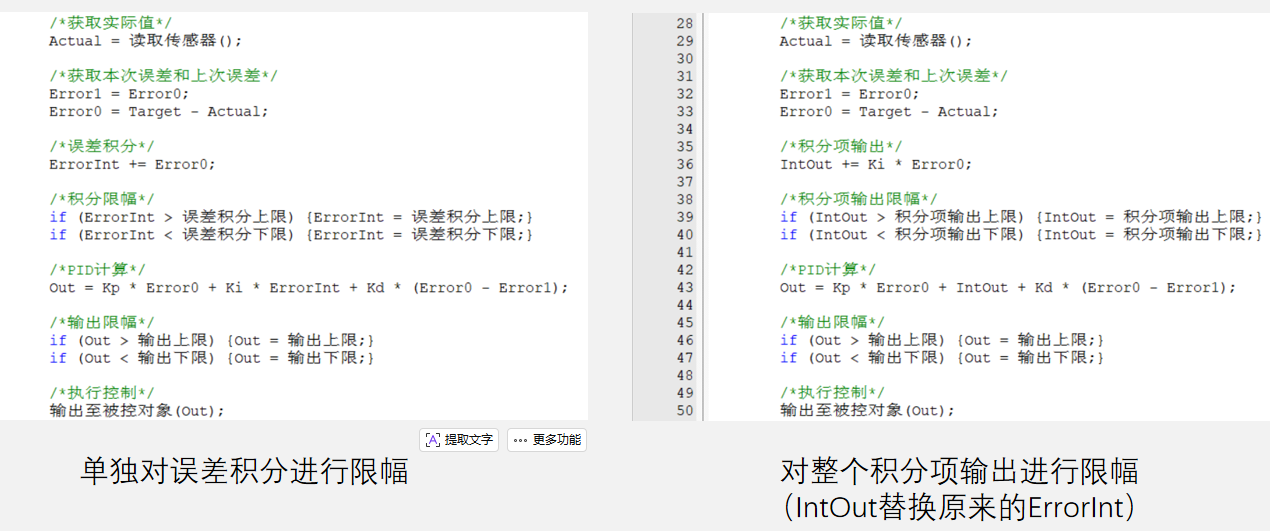
单独对误差积分进行限幅时上下限的确定:
1,实测法:观察正常情况为多少,再给加一点余量
2,计算法:设KP=0,KD=0,OUT/KI=上下限。
对整个积分项输出进行限幅时上下限可以和总输出OUT的上下限保持一致,为100和-100.
积分分离
误差小于一个限度才开始积分,反之去掉积分部分。
调控前期误差大,不需要积分项,调控后期为了消除持续的误差才需要积分项。如果一开始就引入了积分项到后期是积分项会累计较大的调控力,导致超调。
实现思路:判断误差小于一定的阈值时才引入积分项调控,反之将误差积分清零或不加入积分项作用。
使用代码:位置式PID定位置控制
两个问题:1,实际值和目标值无法完全重合,有一点小误差(误差太小,通过KP产生的力太小不足以克服摩擦力驱动电机转动)。2,固定位置的力不强,使用外力可以很轻松的使电机位置改变(还是那个原因,误差小,KP产生的力不足以克服外力保持电机位置不变)。如何解决?当误差持续产生时,输出的力应该持续增大,这样才能确保误差消失。这里加入积分项KI=0.1,可以看到误差消失了看似解决了问题,但是如果再次改变目标值,可以看到超调很严重
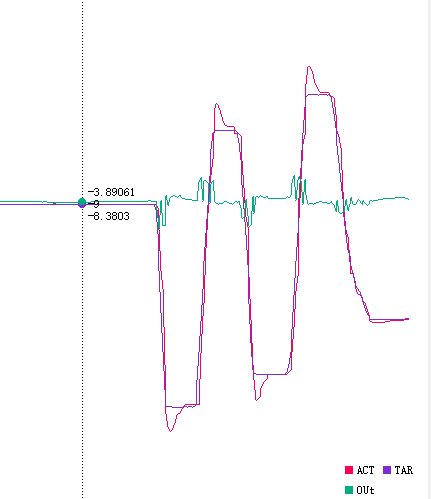
为什么定位置控制加入积分项会出现超调的问题,而定速控制不会出现超调呢?
刚开始误差很大,P项输出较大的力,I项逐渐累积靠近目标值,当实际值等于目标值时,误差为0,P项立即不输出力了,但是I项之前一直在累加,此时形成了最大的正向力,定位置控制需要保持位置不变,不需要输出力,不然位置就不可能恒定,所以此时实际位置必须超过目标位置,超过目标后误差为负P项输出反向的调控力,I项任然输出正向调控力只不过积分项反向积累用于抵消之前累积过大的正向调控力正反积分抵消后,实际值与目标值重合。
定速控制中I项累积的力刚好抵消了摩擦力保持速度的恒定。
一句话总结,定位置控制保持位置恒定不需要输出力,而定速控制要保持速度恒定需要持续输出力来抵抗摩擦力。
如果误差小,使用PID控制器,如果误差大使用PD控制器。
c
void TIM1_UP_IRQHandler(){
static uint8_t count;
if(TIM_GetITStatus(TIM1,TIM_IT_Update)==SET){
count++;
if(count>=40){
count=0;
Actual+=Encoder_Get();//获取当位置
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
if(fabs(ErrorInt)<50){//积分分离,阈值可以通过波形来观察即实际值与目标值的差可以稍微大点
ErrorInt+=Error0;
}else{
ErrorInt=0;
}
Out=Kp*Error0+Ki*ErrorInt+Kd*(Error0-Error1);//位置式PID计算输出
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}
Motor_SetPWM(Out);//设置PWM
}
Key_Tick();
TIM_ClearITPendingBit(TIM1,TIM_IT_Update);
}
}测试:KP=0.4,KI=0.1,KD=0.2 可以看到波形不过冲了
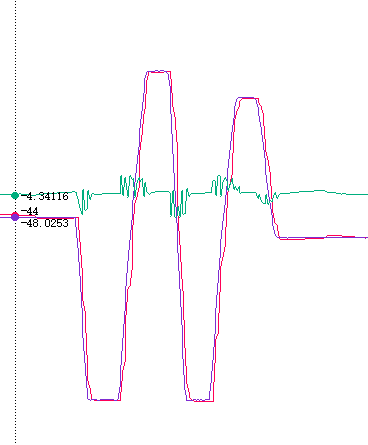
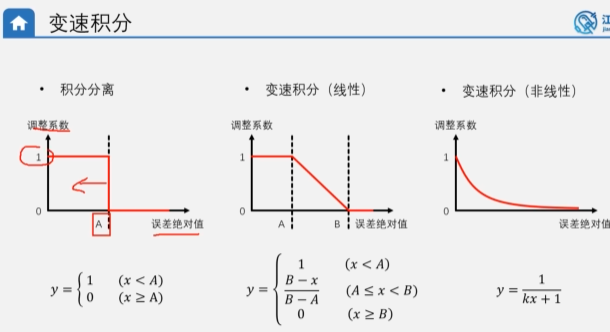
变速积分
问题:如果积分分离的阈值设置的不合理,被控对象刚好在超过这个误差阈值停下来则系统的就没有积分的效果。
比如阈值设置为20 ,小幅度变化目标值有积分效果,当大幅度调整目标值使得误差超过20时积分效果消失了。
解决方式:1,增大阈值
2,设计一个函数 y=1/(Kx+1),x是误差,K是调整系数(0-∞),Y是积分输出,当k=0时输出百分之百的积分效果,K等于无穷大时,y等于0表示没有积分效果,类似于一个可调的开关,随误差的增大积分的效果越不明显,反之误差越小积分效果越明显。
c
Actual+=Encoder_Get();//获取当位置
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
float C =1/(1*fabs(Error0)+1);//积分调整系数
ErrorInt+=C*Error0;//积分项累加时用系数进行调整
Out=Kp*Error0+Ki*ErrorInt+Kd*(Error0-Error1);//位置式PID计算输出
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}微分先行
问题:大幅度调整目标值时,微分项的调控力度大,频繁的大幅度切换目标值时不利于系统稳定。
实现思路:将对误差的微分替换为对实际值的微分
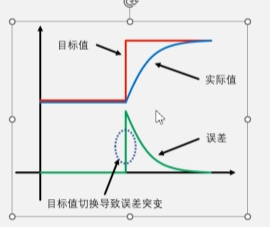
分析一下:目标值突然变化误差突变,D项输出一个斜率为无穷大的正向力,D项表现出来的是反向阻尼的效果,后续从正向调控力又迅速切换到反向调控力,不利于系统稳定。
解决方式:将对误差值的微分变为对实际值的微分,微分项的输入不再是从误差求的,而是提前到从目标值与实际值差值,这就是微分先行。公式中为什么要加入负号?对实际值的微分即求斜率求出来的值是正值,我们需要的是反向的斜率。

c
if(TIM_GetITStatus(TIM1,TIM_IT_Update)==SET){
count++;
if(count>=40){
count=0;
Actual1=Actual;
Actual+=Encoder_Get();//获取当位置
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
if(Ki!=0){//防止积分饱和,导致系统暂时失去控制
ErrorInt+=Error0;
}else{
ErrorInt=0;
}
Difout=-Kd*(Actual-Actual1);
Out=Kp*Error0+Ki*ErrorInt+Difout;//位置式PID计算输出
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}
Motor_SetPWM(Out);//设置PWM
}
Key_Tick();
TIM_ClearITPendingBit(TIM1,TIM_IT_Update);
}实验现象:
纯D项控制时,目标值变化,不会有输出。加入P项后,系统的迟滞感明显增强,这是因为原来对误差的微分在目标切换时会提供一个正向的调控力,加速系统的响应,在使用微分先行后,目标切换时系统的调控力就只有P项了,D项表现为阻尼,阻碍系统的响应速度所以迟滞感增强。
不完全微分
问题:噪声干扰使得误差变化加剧,导致微分项的输出抖动。
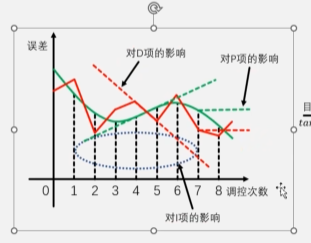
P项调控的是误差值,噪声对P项的影响就是相邻时刻误差的变化量。I项是误差的累积即下方矩形的面积之和。D项是误差的变化趋势即斜率对噪声变化敏感。
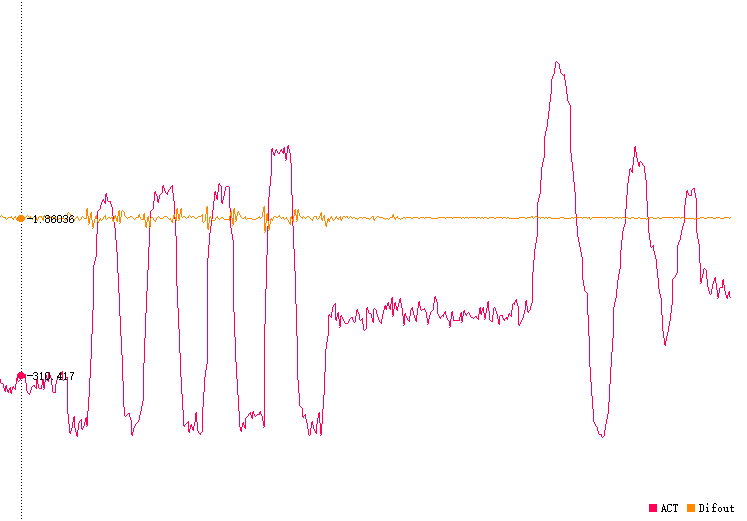
实现思路:给微分项加入一阶惯性单元(低通滤波器)

先试用rand函数(stdlib)生成随机数加给实际值模拟噪声,可以看到D项受噪声影响明显,加入低通滤波器后波形变化更平滑。
c
if(TIM_GetITStatus(TIM1,TIM_IT_Update)==SET){
count++;
if(count>=40){
count=0;
Actual+=Encoder_Get();//获取当位置
Actual+=rand()%41-20;
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
if(Ki!=0){//防止积分饱和,导致系统暂时失去控制
ErrorInt+=Error0;
}else{
ErrorInt=0;
}
DifOut=(1-a)*DifOut+a*Kd*(Error0-Error1);//加入低通滤波器
//DifOut=Kd*(Error0-Error1);//用来对比波形
Out=Kp*Error0+Ki*ErrorInt+DifOut;//位置式PID计算输出
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}
Motor_SetPWM(Out);//设置PWM
} 
输出偏移与输入死区
现象:使用位置式PID定位置控制电机时,实际值与目标值没有完全重合,其次电机稳定下来后输出值不为零,虽然PWM有输出但是输出的力太小不足以克服摩擦力使得实际值与目标值重合。可以在输出值不为0时加入一个固定的偏移让它能克服摩擦力而驱动电机转动。
对于一些需要一定力度的执行器,如果输出值太小,执行器可能无动作,这可能会引起调控误差,降低系统响应速度。
所以在输出为零时正常输出0,在非0输出时,给输出值加一个固定偏移。这个固定的偏移值可以通过实验测到。
c
if(Key_Check(KEY_1,KEY_SINGLE)){
Out+=1;
}else if(Key_Check(KEY_2,KEY_SINGLE)){
Out-=1;
}
Motor_SetPWM(Out);//设置PWM
OLED_Printf(0,16,OLED_8X16,"Out:");
OLED_Printf(40,16,OLED_8X16,"%3.2f",Out);
OLED_Update();实测得到正转偏移为6,反转偏移为8;
c
if(count>=40){
count=0;
Actual+=Encoder_Get();//获取当位置
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
if(Ki!=0){//防止积分饱和,导致系统暂时失去控制
ErrorInt+=Error0;
}else{
ErrorInt=0;
}
Out=Kp*Error0+Ki*ErrorInt+Kd*(Error0-Error1);//位置式PID计算输出
if(Out>0){
Out+=6;
}else if(Out<0){
Out-=8;
}
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}
Motor_SetPWM(Out);//设置PWM
}实际现象:在-8到6之间的输出值不会出现,电机出现抖动。
输入死区:误差小于一个限度是不进行调控,不能因为输入值的噪声波动频繁的进行调控反而使得系统不稳定,当误差值很小时要进行规避。
c
if(TIM_GetITStatus(TIM1,TIM_IT_Update)==SET){
count++;
if(count>=40){
count=0;
Actual+=Encoder_Get();//获取当位置
Error1=Error0;
Error0=Target-Actual;//获取当前值与目标值的误差差
if(fabs(Error0)<5){//输入死区
Out=0;
}else{
if(Ki!=0){//防止积分饱和,导致系统暂时失去控制
ErrorInt+=Error0;
}else{
ErrorInt=0;
}
Out=Kp*Error0+Ki*ErrorInt+Kd*(Error0-Error1);//位置式PID计算输出
if(Out>0){
Out+=6;
}else if(Out<0){
Out-=8;
}
}
if(Out>100){Out=100;}//积分限幅
if(Out<-100){Out=-100;}
Motor_SetPWM(Out);//设置PWM
}实现现象:位置停下来时,实际值与目标值的差值即是输入死区的控制值,输出值OUT为0。利用这种方法也达到了加入I项来调节的效果。
多环串级PID
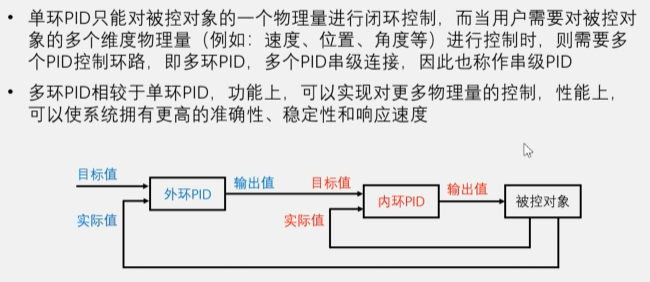
定速控制速度恒定,定位置控制位置不变,如果想电机以指定的速度旋转到指定的位置则需要同时调整两个物理量(速度,位置),这就需要双环PID。
内环PID的输出值作用于被控对象,实际值从被控对象的传感器读取,内环PID的目标值由外环PID的输出值所控制,外环PID的输出值不直接作用于被控对象而是通过控制内环的目标值,间接的作用于被控对象,外环PID的目标值也是从被控对象的传感器获取,外环PID的目标值是用户所控制的输入。
定位置控制单环与双环比较
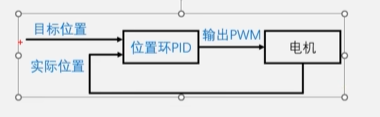
目标位置设定为100,PID检测到实际位置0与目标位置100的误差后输出PWM为正值,驱动电机正转到目标位置,目标位置设定为-100,PID检测到实际位置0与目标位置-100的误差后输出PWM为负值,驱动电机反转到目标位置。
单环PID的缺陷:当实际位置与目标位置很小时,PID输出的PWM很小不足以驱动电机抵抗摩擦力来达到目标位置这就造成了调控误差。其次,当有外力驱动电机时,如果这个保持位置的调控力很小,PID输出的PWM也很小,系统在目标位置抵抗外力的能力不足。
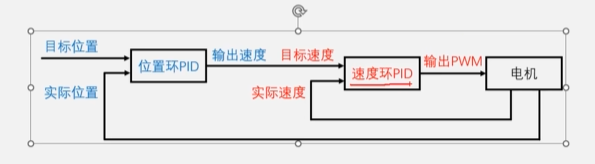
双环PID能有效解决单环PID的缺陷:
将内环速度环和电机看做一个整体,那么这个电机就是一个自带速度闭环控制的电机,输入目标速度与实际速度是线性关系,不存在启动力度的问题,不会因为启动力度太小转不起来的问题,并且电机可以自适应负载,时钟位置转速的稳定。
过程分析:
目标位置,实际位置,目标速度,实际速度起始状态为零。然后用户指定目标位置变为100,首先位置环发现误差为正,因此这里输出值也为一个正值,假设为50,这个50此时表示一个指导内环运转的目标速度。因此速度还受到目标速度设定为50,然后速度环也会检测到误差为正。因此输出pwm为正驱动电机正转,电机正转的同时,实际速度和实际位置都会增加。实际位置会趋近于目标位置,实际速度也会趋近于目标速度,随着实际位置靠近目标位置。位置环输出的目标速度也会逐渐降低,最终实际位置与目标位置稳稳重合。这时位置环输出速度为零,速度环的目标速度为零,电机停下来定位的控制完成。然后我再假设实际位置为零,目标位置很小,此时位置环输出值也很小,但是由于这个值不是直接驱动电机的pwm,而是用于指导速度环的目标速度。所以现在速度环需要控制电机以一个很低的速度转动,由于速度环是pi控制,电机不可能不转所以这里的实际位置必然会与目标位置重合,不会像单环PID那样产生调控误差。最后我们再看双环pid抵抗外力干扰的过程,比如现在位置固定下来了。目标位置和实际位置重合,假设为100。目标速度和实际速度依次为零。然后我用手强行改变位置,比如实际位置正向增加到105了,那么位置一旦正向改变,必然首先会产生实际速度大于零,这时速度环就会输出负向力来对抗外敌。维持目标速度为零的状态,其次位置正向改变还会使位置环实际值大于目标值,因此位置环会输出一个负的速度值给到速度环。原来目标速度为零时,速度环就已经开始输出反向力了,现在目标速度变为负值,就会输出更大的反向力?再者速度还有积分项,如果实际速度不能达到目标,速度,速度还会进一步增加反向作用力,这几个方向力共同作用可以瞬间让电机对抗外界的力变得很大。双环pid的位置控制,用手去改变位置,可以感受到非常大的阻力。这个位置控制的可以说是稳如泰山,一旦有外力改变位置,速度环会优先响应,位置环在紧随其后。两者共同作用能够使位置闭环控制,又快又有劲。
双环PID代码实现
使用定时器定时1ms,在定时器中断中分频分别进行内外环的调控,一般外环调控周期要大于内环调控周期(外环的输出给内环,外环太快没有用,其次内环要求更灵敏)。
内外环调控所使用的变量相互独立。外环的输入是电位器的实际读取的位置值(+408~ -408),外环的输出要作为内环的输入就需要调整外环的输出范围,实测目标速度180个边沿/40毫秒,留出调控余量输出限幅为(+150 ~ -150)。内环读取实际速度通过累加后得到实际位置,这个实际位置成了外环的目标位置,内环的输出作用与被控对象。
调参时 ,为了避免内外环相互干扰,每次只调节一个环的参数。
内环定速控制,这个速度的设定就是通过外环的输出限幅。
c
// OuterTarget=RP_GetValue(4)/4095.0*816 -408;//一圈408个计数,这个值作为外环的目标值
void TIM1_UP_IRQHandler(){
static uint8_t count1,count2;
if(TIM_GetITStatus(TIM1,TIM_IT_Update)==SET){
count1++;
if(count1>=40){
count1=0;
Speed=Encoder_Get();//获取当前速度
Location+=Speed;//速度累加得到位置,这个值作为外环的实际值
InnerActual=Speed;
InnerError1=InnerError0;
InnerError0=InnerTarget-InnerActual;//获取当前值与目标值的误差差
if(InnerKi!=0){//防止积分饱和,导致系统暂时失去控制
InnerErrorInt+=InnerError0;
}else{
InnerErrorInt=0;
}
InnerOut=InnerKp*InnerError0+InnerKi*InnerErrorInt+InnerKd*(InnerError0-InnerError1);//位置式PID计算输出
if(InnerOut>100){InnerOut=100;}//积分限幅
if(InnerOut<-100){InnerOut=-100;}
Motor_SetPWM(InnerOut);
}
count2++;
if(count2>=40){
count2=0;
OuterActual=Location;//获取当前位置
OuterError1=OuterError0;
OuterError0=OuterTarget-OuterActual;
if(OuterKi!=0){//防止积分饱和,导致系统暂时失去控制
OuterErrorInt+=OuterError0;
}else{
OuterErrorInt=0;
}
OuterOut=OuterKp*OuterError0+OuterKi*OuterErrorInt+OuterKd*(OuterError0-OuterError1);
if(OuterOut>150){OuterOut=150;}//外环的输出给到内环的输入,内环速度最大可以给180,这里留余量给150
if(OuterOut<-150){OuterOut=-150;}
InnerTarget=OuterOut;
}
Key_Tick();
TIM_ClearITPendingBit(TIM1,TIM_IT_Update);
}
}