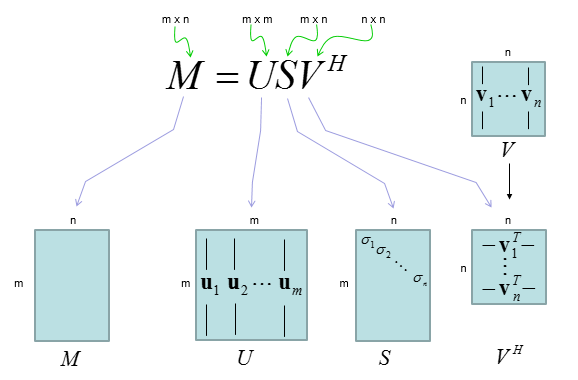
假设"M矩阵"指的是一个任意矩阵,奇异值分解(SVD)就是一种方法,能把这个矩阵"拆解"成三个更简单的矩阵:U、Σ(读作Sigma)和V^T。通俗地说,这就像把一张复杂照片拆成"框架"(U)、"重要程度列表"(Σ)和"图案模板"(V^T)。最终,你可以用这三个部分重新拼回原矩阵,但过程中能看到哪些部分是最关键的,能帮你压缩数据或找出隐藏模式。
为什么叫"拆解"?因为SVD不是随意切分,而是基于数学原理,让分解后的部分捕捉矩阵的"本质"。它适用于任何形状的矩阵(不一定是方形的),超级实用。比如,在图像处理中,它能帮你去除噪音;在推荐系统中,能找出用户偏好。
下面我用一个 具体的数值例子,把图里的
完整拆出来(这里是实数矩阵,所以 )。
例子:M 是 3×2
取矩阵:
SVD 要把它拆成:
其中尺寸对应为:
-
-
-
,且
计算结果(数值版 SVD)
1) 奇异值矩阵 S
该矩阵的两个奇异值为:
所以:
2) 右奇异向量矩阵 V 与 
因此
3) 左奇异向量矩阵 U
最终:完整的 LaTeX 拆解表达式
补充:更常用的"经济型 SVD"(更贴合机器学习)
因为 M 是 3×2,其实只需要前 n=2 个方向:
-
(取 U 的前两列)
-
-
更"直观"的,还可以解释成一句话:
:把输入坐标系旋转到"最合适的方向" →
S:沿两个主方向拉伸(一个拉得大,一个拉得小) →
U:再把结果旋转到输出坐标系
下面演示如何从 手算出 V 和奇异值 σ (也就是 S 的对角线),一步一步写清楚 ✅
例子矩阵
SVD:
第 1 步:先算 
第 2 步:解特征值(得到 λ,再开方得 σ)
特征方程:
展开:
(2.1)λ 是什么?
这里的 是 单位矩阵 (跟
同维度,都是 2×2):
所以
(2.2)做矩阵相减:
所以就是:
(2.3)最后对它取行列式
因此:
展开:
解这个二次方程:
所以两条特征值:
✅ 奇异值 = 特征值开平方
于是(注意 S 是 3×2):
第 3 步:解特征向量(得到 V)
我们对每个 λ,解:
(3.1) 对  求 v1
求 v1
用第一行:
代入
(3.2)关键点:这不是一个"唯一解",而是一整条直线方向
因为它只是说:
这说明所有满足条件的 (x,y) 都在同一条过原点的直线上:
也就是说:
(3.3)为什么可以直接令 x=1?
因为特征向量只关心"方向",不关心长度。
如果 v 是特征向量,那么任意非零倍数 cv 仍然是特征向量:
所以我们可以选择一个最方便的尺度,比如令:
x=1
那么:
于是得到一个"代表方向"的向量:
这里的符号 ∝ 的意思是:
"成比例 / 同方向"
(差一个任意非零倍数都算同一个特征向量方向)
(3.4)为什么会出现近似数值 0.7543?
我们把
算成小数:
所以:
我们就把v1继续一步步变成"单位特征向量"(也就是 SVD 里真正用的那种 v1),并解释为什么变成了带负号的版本。
单位化(长度变成 1),可取:
(3.5)"∝" 的意思:方向对了,但长度随便
意思是:真正的特征向量可以是它的任何非零倍数,比如
它们都在同一条直线上,方向一致。
(3.6)为什么要"单位化"(归一化)?
在 SVD 里,V 要满足正交条件:
所以它的列向量必须是单位向量:
因此我们要把向量缩放到长度 1。
(3.7)计算长度 ∥v1∥
先记:
它的长度是:
(3.8)单位化:除以长度
单位向量定义:
所以:
✅ 这就是"标准的单位特征向量版本"。
(3.9)为什么之前写的是负号版本?
我写的是:
原因只有一个:
✅ 特征向量整体乘 −1 仍然是特征向量
因为如果:
那么两边同乘 −1:
依然成立。
所以:
二者完全等价,只是方向箭头反过来了(同一条直线)。
✅ 总结一句话(最关键的直觉)
从 y=kx 推出向量方向
因为把 x 提出来:
所以特征向量可以写成:
所以特征向量方向为:
(3.10) 对  求 v2
求 v2
同样:
所以:
✅ 组成 V
把 v1,v2 作为列拼起来:
第 4 步:用  得到 U
得到 U
这个很关键,因为它解释了"为什么 U 会出现":
怎么计算 u1,u2?
(4.1)计算 u1
先算 Mv1
再除以 σ1
(4.2)计算 u2
先算 Mv2
再除以 σ2
✅ 那么 u3 怎么来的?(因为这里 M 是 3×2)
因为 U 在"完整版 SVD"里要是 3×3 的正交矩阵:
但我们只从 得到前两列 u1,u2,还缺一个 u3。
关键事实:
u3 只需要满足:
✅ 在 3D 里最简单的办法:用叉积(cross product)
在三维空间里:
因为叉积天生就同时垂直于两者。
代入数值:
计算得到:
(它本身几乎就是单位长度,必要时再除以 做归一化即可)
于是:
✅ 最终完整拆解
下面我把 逐项乘出来,让你看到它真的就是"乘完正好等于 σu" 的那种一致性:
已知
1)左边:逐项算 
现在每一行都算出来:
第 1 行
第 2 行
第 3 行
所以:
2)右边:逐项算 
逐项乘:
第 1 项
第 2 项
第 3 项
所以:
✅ 对齐验证:两边完全相等(误差仅来自四舍五入)
同样可逐项验算。