控制系统建模仿真（三）：矩阵分析、微分方程与最优化求解

文章目录

• 前言
• [一、 矩阵分析与基础运算](#一、 矩阵分析与基础运算)
• • [1. `det(A)` ------ 行列式计算](#1. det(A) —— 行列式计算)
  • [2. `rank(A)` ------ 矩阵的秩](#2. rank(A) —— 矩阵的秩)
  • [3. `eig(A)` ------ 特征值与特征向量](#3. eig(A) —— 特征值与特征向量)
  • [4. `expm(A)` ------ 矩阵指数运算](#4. expm(A) —— 矩阵指数运算)
• [二、 方程求解（线性与矩阵方程）](#二、 方程求解（线性与矩阵方程）)
• • [5. `\` (左除运算符) ------ 求解线性方程组](#5. \ (左除运算符) —— 求解线性方程组)
  • [6. `lyap(A, Q)` ------ 求解 Lyapunov 方程](#6. lyap(A, Q) —— 求解 Lyapunov 方程)
  • [7. `fsolve` ------ 数值求解非线性方程组](#7. fsolve —— 数值求解非线性方程组)
• [三、 微分方程数值解 (ODE)](#三、 微分方程数值解 (ODE))
• • [8. `ode45` ------ 常微分方程求解器](#8. ode45 —— 常微分方程求解器)
  • • • [9. `ode15s` ------ 刚性微分方程求解器](#9. ode15s —— 刚性微分方程求解器)
• [四、 最优化问题](#四、 最优化问题)
• • [10. `fmincon` ------ 带约束的非线性最小化](#10. fmincon —— 带约束的非线性最小化)
  • [11. `lsqcurvefit` ------ 非线性最小二乘拟合](#11. lsqcurvefit —— 非线性最小二乘拟合)
• [五、 拉普拉斯变换](#五、 拉普拉斯变换)
• • [12. `laplace` / `ilaplace` ------ 符号变换](#12. laplace / ilaplace —— 符号变换)
• 学习核心建议：

前言

欢迎进入第三章：科学运算问题的MATLAB求解。前面第一章和第二章我们学习MATLAB与simulink的基本入门以及各种基础函数，这节课我们进入系统阐述的科学运算问题的MATLAB求解，如果没有学过前两篇博客的话，可以直接开始，也可以通过系列的链接进入第一章和第二章的博客进行学习。

如果说第一章是带你"看房子"，那么第二章就是教你"打地基"。那本章就是真正运用这些东西来做实实在在的解决一些问题。接下来我们开始：

---

一、 矩阵分析与基础运算

1. det(A) ------ 行列式计算

• 功能与用处：计算方阵的行列式，常用于判定矩阵是否可逆（非零则可逆）。

• 输入输出 ：输入为方阵 A；返回标量。

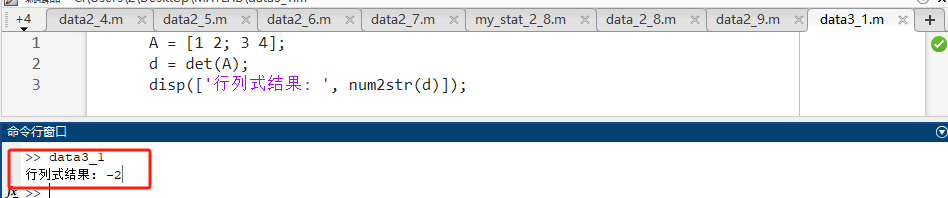
• 代码示例 ：

  A = [1 2; 3 4];
  d = det(A);
  disp(['行列式结果: ', num2str(d)]);

• 源码讲解 ：直接调用内置函数计算。输出结果为 1*4 - 2*3 = -2。

• 预期输出 ：行列式结果: -2
  

2. rank(A) ------ 矩阵的秩

• 功能与用处 ：求矩阵的秩，在控制理论中用于判定系统的可控性 和可观测性。

• 输入输出 ：输入矩阵 A；返回整数秩。

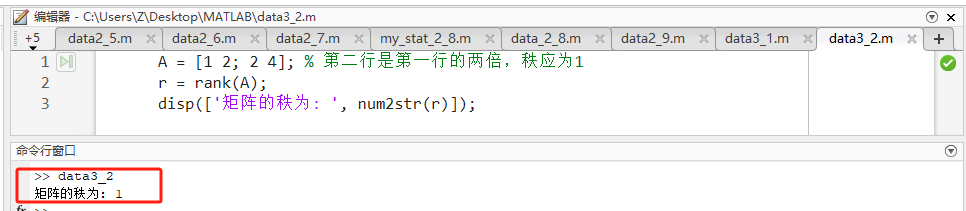
• 代码示例 ：

  A = [1 2; 2 4]; % 第二行是第一行的两倍，秩应为1
  r = rank(A);
  disp(['矩阵的秩为: ', num2str(r)]);

• 源码讲解：该函数通过SVD分解计算非零奇异值的个数。

• 预期输出 ：矩阵的秩为: 1
  

3. eig(A) ------ 特征值与特征向量

• 功能与用处 ：计算矩阵的特征值，在控制系统中特征值直接对应系统的极点，决定稳定性。

• 输入输出 ：输入方阵 A；返回特征值向量 V 或特征向量阵 X 与特征值对角阵 D。

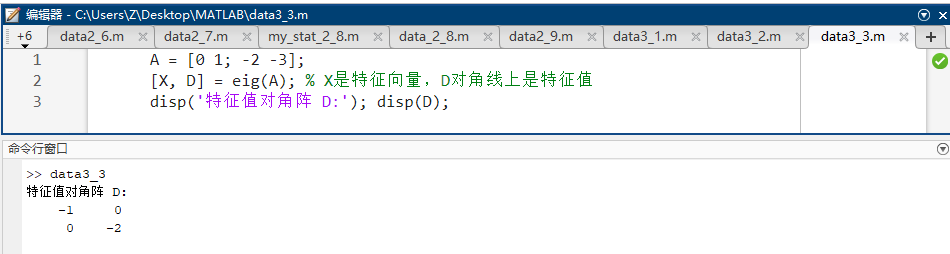
• 代码示例 ：

  A = [0 1; -2 -3];
  [X, D] = eig(A); % X是特征向量，D对角线上是特征值
  disp('特征值对角阵 D:'); disp(D);

• 源码讲解 ：对于线性系统 x ˙ = A x \dot{x}=Ax x˙=Ax，特征值即系统的自然频率/极点。此处结果为 -1 和 -2。

• 预期输出 ：D = [-1 0; 0 -2]
  

4. expm(A) ------ 矩阵指数运算

• 功能与用处 ：计算矩阵指数 e A e^{A} eA，是求解状态转移矩阵 Φ ( t ) = e A t \Phi(t) = e^{At} Φ(t)=eAt 的核心函数。

• 输入输出 ：输入方阵 A；返回同维矩阵。

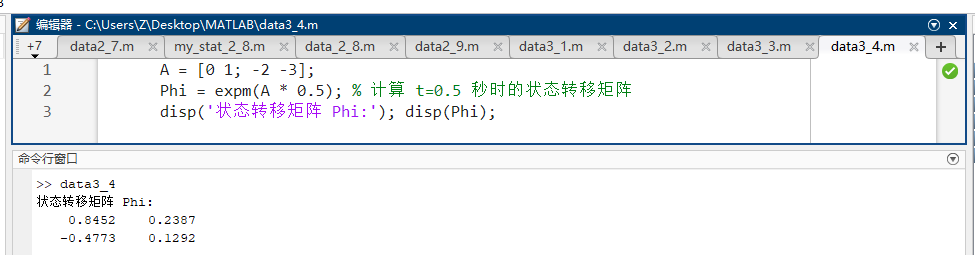
• 代码示例 ：

  A = [0 1; -2 -3];
  Phi = expm(A * 0.5); % 计算 t=0.5 秒时的状态转移矩阵
  disp('状态转移矩阵 Phi:'); disp(Phi);

• 源码讲解 ：注意 ：expm 是矩阵幂级数运算，而 exp 是对每个元素单独求幂。在控制工程中必须使用 expm。

• 预期输出 ：一个 2 × 2 2 \times 2 2×2 的数值矩阵。
  

---

二、 方程求解（线性与矩阵方程）

5. \ (左除运算符) ------ 求解线性方程组

• 功能与用处 ：求解 A x = b Ax = b Ax=b，是计算系统平衡点最快捷的方法。

• 输入输出 ：输入系数阵 A 和常数项 b；返回解向量 x。

• 代码示例 ：

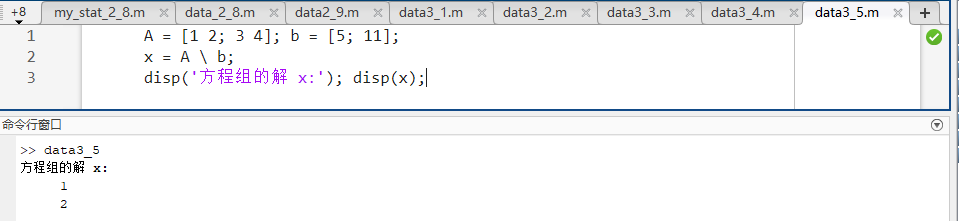
  A = [1 2; 3 4]; b = [5; 11];
  x = A \ b;
  disp('方程组的解 x:'); disp(x);

• 源码讲解 ：MATLAB 内部根据 A 的性质自动选择 LU 分解或 QR 分解，比 inv(A)*b 更稳定高效。

• 预期输出 ：x = [1; 2]
  

6. lyap(A, Q) ------ 求解 Lyapunov 方程

• 功能与用处 ：求解 A X + X A T + Q = 0 AX + XA^T + Q = 0 AX+XAT+Q=0，用于线性系统的稳定性分析。

• 输入输出 ：输入系统阵 A 和对称阵 Q；返回解矩阵 X。

• 代码示例 ：

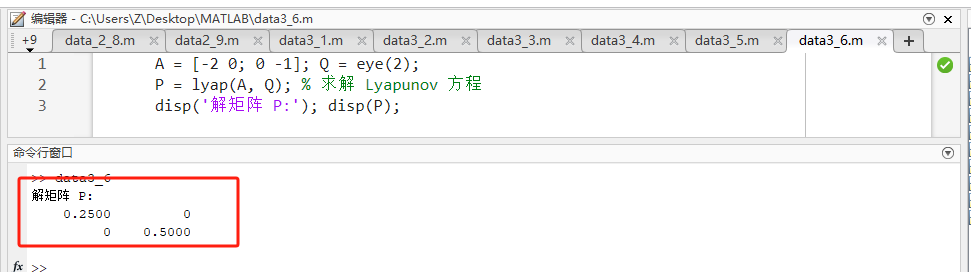
  A = [-2 0; 0 -1]; Q = eye(2);
  P = lyap(A, Q); % 求解 Lyapunov 方程
  disp('解矩阵 P:'); disp(P);

• 源码讲解 ：如果 A A A 是稳定的（特征值均有负实部），且 Q Q Q 正定，则 P P P 必正定。

• 预期输出 ：P = [0.25 0; 0 0.5]
  

7. fsolve ------ 数值求解非线性方程组

• 功能与用处 ：寻找非线性函数 f ( x ) = 0 f(x)=0 f(x)=0 的数值根，用于非线性控制系统的平衡点计算。

• 输入输出 ：输入匿名函数句柄和初值 x0；返回解 x。

• 代码示例 ：

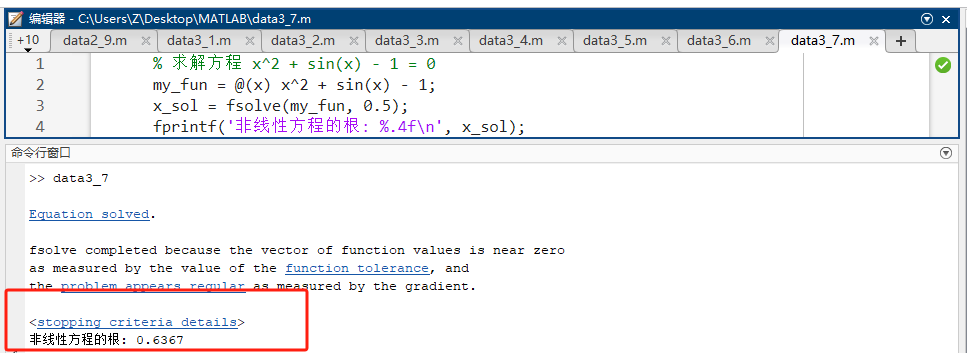
  % 求解方程 x^2 + sin(x) - 1 = 0
  my_fun = @(x) x^2 + sin(x) - 1;
  x_sol = fsolve(my_fun, 0.5); 
  fprintf('非线性方程的根: %.4f\n', x_sol);

• 源码讲解：使用拟牛顿法迭代，非常依赖初值的选取。

• 预期输出 ：非线性方程的根: 0.6367
  

---

三、 微分方程数值解 (ODE)

8. ode45 ------ 常微分方程求解器

• 功能与用处 ：最通用的微分方程数值解函数，用于时域系统仿真。

• 输入输出 ：输入方程句柄 f(t,x)、时间范围 [t0 tf]、初值 x0；返回时间点 t 和状态值 x。

• 代码示例 ：

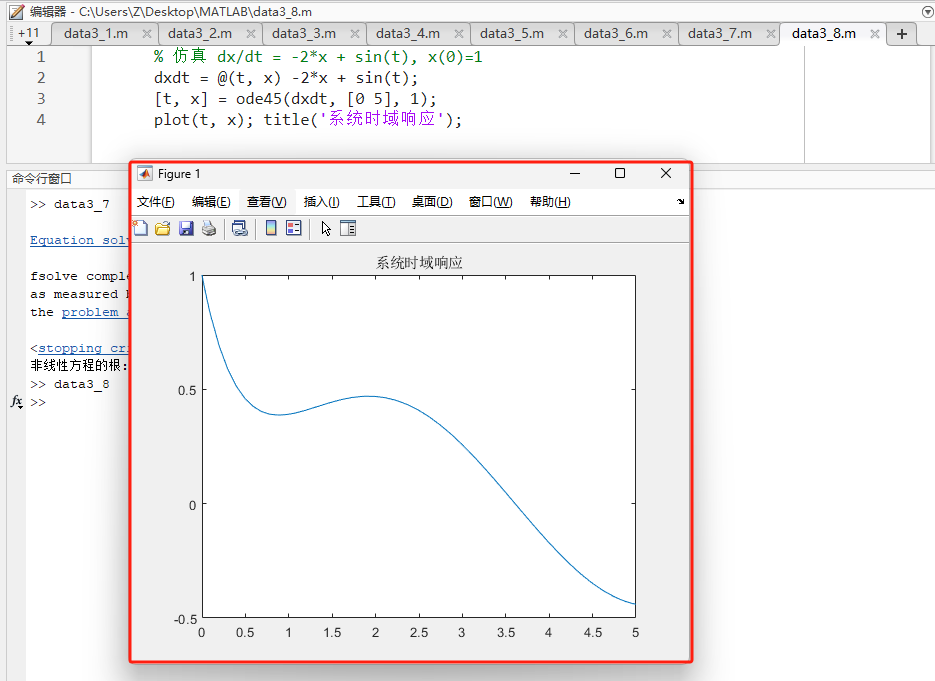
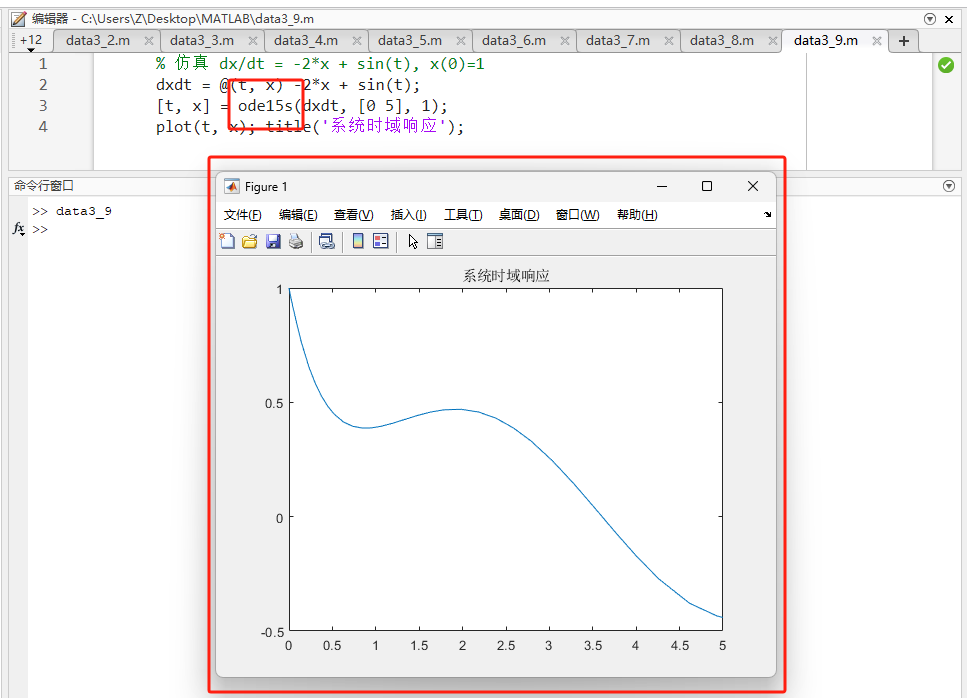
  % 仿真 dx/dt = -2*x + sin(t), x(0)=1
  dxdt = @(t, x) -2*x + sin(t);
  [t, x] = ode45(dxdt, [0 5], 1);
  plot(t, x); title('系统时域响应');

• 源码讲解：采用变步长的 4-5 阶龙格-库塔法（Runge-Kutta），在精度和速度间取得平衡。

• 预期输出 ：一段平滑下降并随正弦波波动的曲线图。
  

9. ode15s ------ 刚性微分方程求解器

• 功能与用处：求解"刚性"（Stiff）方程，即系统中同时存在极快和极慢动态的情形。

• 输入输出 ：参数同 ode45。

• 代码示例 ：用于某些极高增益的控制系统仿真，当 ode45 运行极慢或报错时，换用此函数。

• 代码示例 ：

  % 仿真 dx/dt = -2*x + sin(t), x(0)=1
  dxdt = @(t, x) -2*x + sin(t);
  [t, x] = ode15s(dxdt, [0 5], 1);
  plot(t, x); title('系统时域响应');

• 源码讲解：采用变步长的 4-5 阶龙格-库塔法（Runge-Kutta），在精度和速度间取得平衡。

• 预期输出 ：一段平滑下降并随正弦波波动的曲线图。
  

---

四、 最优化问题

10. fmincon ------ 带约束的非线性最小化

• 功能与用处 ：在给定的约束下寻找函数极小值，控制系统中用于性能指标优化（如 PID 调优）。

• 输入输出：目标函数、初值、线性/非线性约束；返回最优参数。

• 代码示例 ：

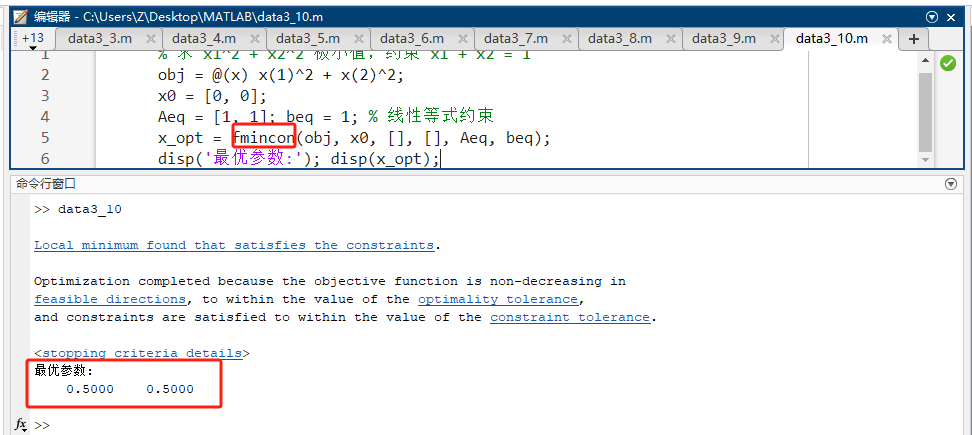
  % 求 x1^2 + x2^2 极小值，约束 x1 + x2 = 1
  obj = @(x) x(1)^2 + x(2)^2;
  x0 = [0, 0];
  Aeq = [1, 1]; beq = 1; % 线性等式约束
  x_opt = fmincon(obj, x0, [], [], Aeq, beq);
  disp('最优参数:'); disp(x_opt);

• 源码讲解：这是工程中最强大的优化工具，可以处理复杂的边界和约束。

• 预期输出 ：最优参数: [0.5 0.5]
  

11. lsqcurvefit ------ 非线性最小二乘拟合

• 功能与用处 ：根据实验数据拟合模型参数，常用于系统辨识。

• 输入输出 ：模型函数、待定参数初值、样本数据 x , y x, y x,y；返回拟合参数。

• 代码示例 ：

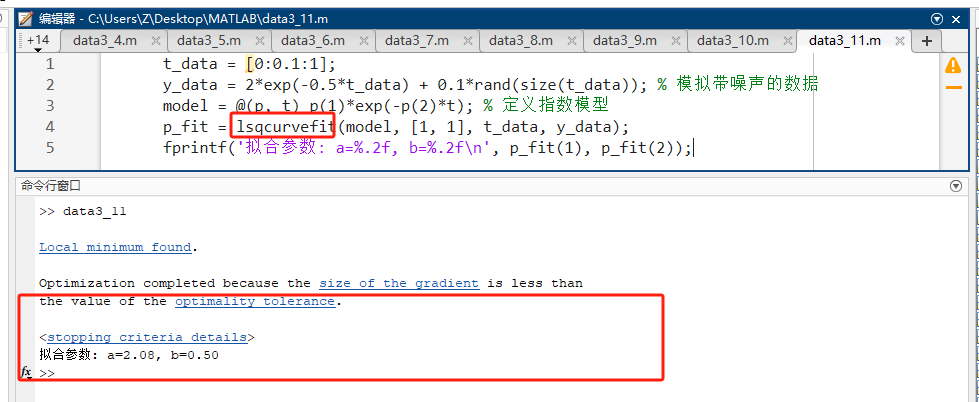
  t_data = [0:0.1:1]; 
  y_data = 2*exp(-0.5*t_data) + 0.1*rand(size(t_data)); % 模拟带噪声的数据
  model = @(p, t) p(1)*exp(-p(2)*t); % 定义指数模型
  p_fit = lsqcurvefit(model, [1, 1], t_data, y_data);
  fprintf('拟合参数: a=%.2f, b=%.2f\n', p_fit(1), p_fit(2));

• 源码讲解 ：寻找使误差平方和最小的参数 p。

• 预期输出 ：拟合参数: a=2.0x, b=0.5x（接近真实值）。
  

---

五、 拉普拉斯变换

12. laplace / ilaplace ------ 符号变换

• 功能与用处 ：在时域表达式和 s s s 域传递函数之间进行解析转换。

• 输入输出：符号表达式；返回变换后的符号结果。

• 代码示例 ：

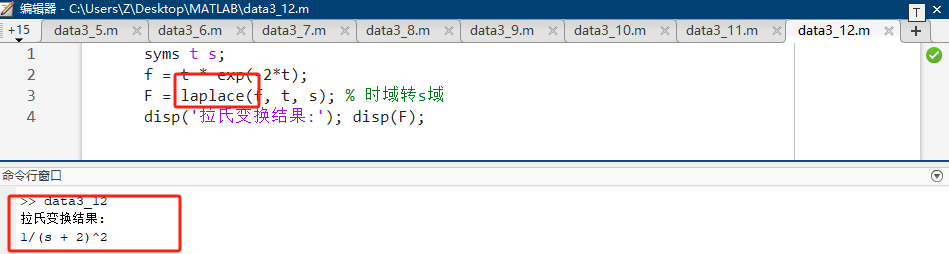
  syms t s;
  f = t * exp(-2*t);
  F = laplace(f, t, s); % 时域转s域
  disp('拉氏变换结果:'); disp(F);

• 源码讲解：基于符号计算引擎，给出的结果是代数式而非数值。

• 预期输出 ：1/(s + 2)^2
  

---

学习核心建议：

1. 区分数值与符号 ：fsolve（数值解）和 solve（符号解）用法完全不同，控制系统仿真多用数值解。
2. 句柄使用 ：掌握 @(变量) 表达式 这种写法，它是调用 ode45 等高级函数的通行证。
3. 矩阵方程 ：在现代控制理论中，lyap 和 care（求解 Riccati 方程）比手动推导公式重要得多。

当你掌握了这些数学工具，第四章我们将开始正式构建控制系统的传递函数和状态空间模型。准备好继续了吗？