练题100天——DAY40：合并两个有序链表

刚刚学完链表，因为每天上课以及还有其他作业，所以我决定------从今天开始每天打卡至少一道链表的题目。后续把链表的简单题做完，会将所有题再整理到一起，在那之前，每天应该之后更新一道题。

一.合并有序链表 ★★★☆☆

题目

21. 合并两个有序链表将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

我的思路

创建一个ListNode*类型的变量res，用来保存合并后的链表。遍历两个链表list1和list2，将值更小的链表指针的值和地址都赋给res，同时移动链表的指针，直到一个链表为空，退出循环，处理还有数据的链表，将剩下的值赋给res。

代码

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        // 一一比较，小的放到新链表中
        ListNode* res;
        while (list1->next != nullptr && list2->next != nullptr) {
            if (list1->val < list2->val) {
                res->val = list1->val;
                res = list1;
                list1 = list1->next;
            } else {
                res->val = list2->val;
                res = list2;
                list2 = list2->next;
            }
        }
        while (list1->next != nullptr) {
            res->val = list1->val;
            res = list1;
            list1 = list1->next;
        }
        while (list2->next != nullptr) {
            res->val = list2->val;
            res = list2;
            list2 = list2->next;
        }
        return res;
    }
};

错误原因

对 NULL 指针执行 -> 成员访问，创建的res指针为空

修改

创建一个哑结点dummy，固定新链表的头（避免处理空链表的边界），拼接完之后释放dummy内存，避免内存泄漏。

源代码的其他错误及修正：

1.尝试修改val值，不符合链表拼接的理念：

2.当一个链表为空时，再一个一个结点赋值，属于多余操作

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        // 创建哑结点，避免新建指针为空
        ListNode* dummy = new ListNode(-1);
        ListNode* cur = dummy; // 初始指向哑结点
        // 遍历链表
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next; // 向后移动
            } else {
                cur->next = list2;
                list2 = list2->next; // 向后移动
            }
            cur = cur->next;
        }
        // 拼接剩余链表
        cur->next = list1 != nullptr ? list1 : list2;
        // res链表"继承"哑结点后的链表
        ListNode* res = dummy->next;
        // 释放哑结点，避免内存泄漏
        delete dummy;
        return res;
    }
};

复杂度

n 和 m 分别为两个链表的长度

时间复杂度：O(n+m)。会将两个链表的结点都遍历一遍，所以时间复杂度为O(n+m)，其他操作的时间复杂度为O(1)。

空间复杂度：O(1)。只有哑结点是额外创建的结点，其他结点都是原链表的结点，所以额外内存开销为常数级，所以空间复杂度为O(1)。

官方题解

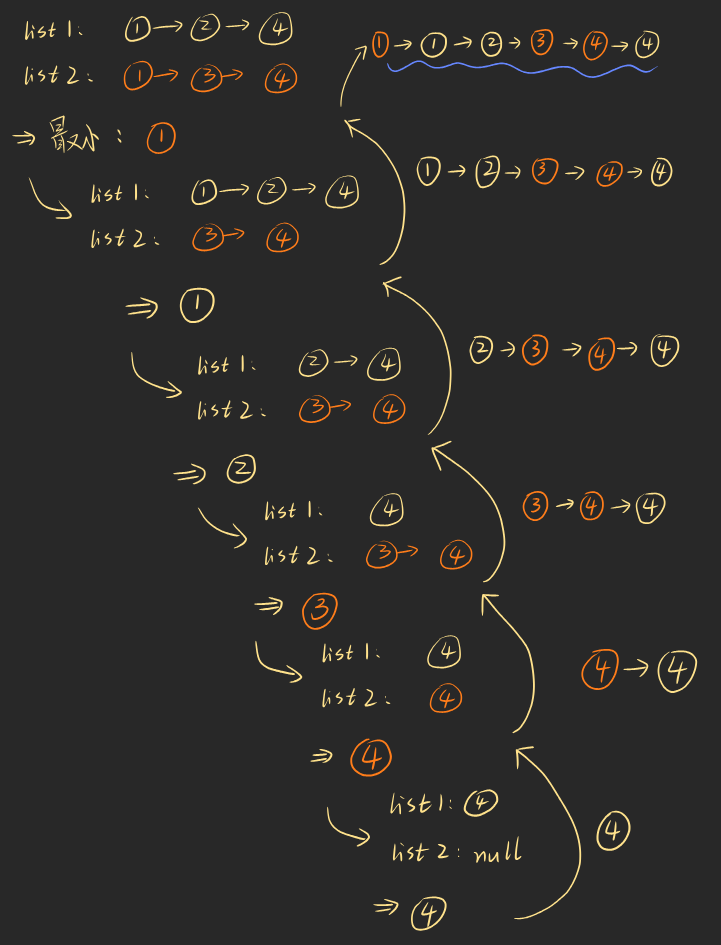
方法一：递归

假设两个链表都不为空，那么两个链表拼接所得的链表可以看作：先选出最小值，并把该结点排除在外，再使剩余的链表合并....

因为两个链表已经是有序的，所以选择最小值，就是两个链表第一个结点的较小值。

如果其中一个链表为空，就返回另一个链表，也作为递归的返回条件。

可以借助下图理解

代码

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        //先判空
        if(list1==nullptr){
            return list2;
        }else if(list2==nullptr){
            return list1;
        }
        //比较第一个结点的值
        else if(list1->val<list2->val){
            list1->next=mergeTwoLists(list1->next,list2);
            return list1;
        }else{
            list2->next=mergeTwoLists(list1,list2->next);
            return list2;
        }
    }
};

复杂度

n 和 m 分别为两个链表的长度

时间复杂度：O(n+m)。至多只会递归调用每个结点一次。

空间复杂度：O(n+m)。递归调用函数需要栈空间，栈空间的大小取决于递归调用的深度，结束递归调用时 mergeTwoLists 函数最多调用 n+m 次，因此空间复杂度为 O(n+m)。

方法2：迭代

通过代码可以看出我的思路跟这个方法一致。

当 list1 和 list2 都不是空链表时，判断 list1 和 list2 哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

结果就是修改比较后较小结点的前驱的next的值，实现将两个链表有序的拼接为一个链表。

不太理解的可以去看看官方题解的动画，很明了。

代码

cpp 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        //设定哨兵结点
        ListNode* prehead = new ListNode(-1);
        ListNode* prev = prehead;
        // 遍历链表
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val < list2->val) {
                prev->next = list1;
                list1 = list1->next;
            } else {
                prev->next = list2;
                list2 = list2->next;
            }
            prev = prev->next;
        }
        // 拼接剩余链表
        prev->next = list1 != nullptr ? list1 : list2;
        
        return prehead->next;
    }
};

复杂度

n 和 m 分别为两个链表的长度

时间复杂度：O(n+m)。其中 n 和 m 分别为两个链表的长度。因为每次循环迭代中，list1 和 list2 只有一个元素会被放进合并链表中，因此 while 循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为 O(n+m)。

空间复杂度：O(1)。只需要常数的空间存放若干变量。