数据结构——例子求算法时间复杂度&&空间复杂度

>> 求时间复杂度

例1（求斐波那契）

一、分析函数的递归逻辑

函数 foo(n) 是分治型递归函数，核心执行逻辑：

1. 递归终止条件：n≤1n \le 1n≤1 时，仅做赋值返回，是常数级操作 O(1)O(1)O(1)；
2. 递归调用逻辑：n>1n > 1n>1 时，执行 foo(n/2) + foo(n/2)，即连续调用2次 foo(n/2) ，无其他额外复杂操作（加法/赋值均为常数级 O(1)O(1)O(1)）。

---

二、定义时间复杂度的递推公式

设 T(n)T(n)T(n) 为函数处理输入规模为 nnn 的数据时的时间复杂度 ，根据上述逻辑，写出严格的递推关系式：
{T(n)=O(1)n≤1（基准条件：递归终止）T(n)=2⋅T(n2)+O(1)n>1（递归条件：2次子问题+常数操作） \begin{cases} T(n) = O(1) \quad &n \le 1 \quad \text{（基准条件：递归终止）} \\ T(n) = 2 \cdot T(\frac{n}{2}) + O(1) \quad &n > 1 \quad \text{（递归条件：2次子问题+常数操作）} \end{cases} {T(n)=O(1)T(n)=2⋅T(2n)+O(1)n≤1（基准条件：递归终止）n>1（递归条件：2次子问题+常数操作）

---

三、递推公式展开推导（最易懂的方法）

为了简化计算，我们用常数 CCC 替代 O(1)O(1)O(1)（所有常数级操作复杂度等价），递推展开：

1. T(n)=2T(n2)+CT(n) = 2T(\frac{n}{2}) + CT(n)=2T(2n)+C
2. 将 T(n2)=2T(n4)+CT(\frac{n}{2}) = 2T(\frac{n}{4}) + CT(2n)=2T(4n)+C 代入，得：T(n)=2[2T(n4)+C]+C=4T(n4)+2C+CT(n) = 2\left[2T(\frac{n}{4})+C\right]+C = 4T(\frac{n}{4}) + 2C + CT(n)=2[2T(4n)+C]+C=4T(4n)+2C+C
3. 再将 T(n4)=2T(n8)+CT(\frac{n}{4}) = 2T(\frac{n}{8}) + CT(4n)=2T(8n)+C 代入，得：T(n)=8T(n8)+4C+2C+CT(n) = 8T(\frac{n}{8}) + 4C + 2C + CT(n)=8T(8n)+4C+2C+C
4. 以此类推，推到第 kkk 步 ，得到通用规律：
   T(n)=2k⋅T(n2k)+C⋅(2k−1)T(n) = 2^k \cdot T\left(\frac{n}{2^k}\right) + C\cdot(2^k-1)T(n)=2k⋅T(2kn)+C⋅(2k−1)

关键：找到递归终止的临界条件

当 n2k≤1\frac{n}{2^k} \le 12kn≤1 时，递归终止（触发 n≤1n \le 1n≤1 的基准条件），此时：
n2k=1  ⟹  2k=n  ⟹  k=log⁡2n\frac{n}{2^k}=1 \implies 2^k = n \implies k = \log_2n2kn=1⟹2k=n⟹k=log2n

代入临界条件完成推导

已知 T(1)=CT(1)=CT(1)=C，2k=n2^k=n2k=n，代入得：
T(n)=n⋅C+C⋅(n−1)=C⋅(2n−1) \begin{align*} T(n) &= n \cdot C + C\cdot(n-1) \\ &= C\cdot(2n-1) \end{align*} T(n)=n⋅C+C⋅(n−1)=C⋅(2n−1)

根据时间复杂度的定义，忽略常数系数和低阶项 ，最终 T(n)=O(n)T(n) = \boldsymbol{O(n)}T(n)=O(n)。

---

四、补充：主定理（Master 定理）快速秒杀

本题的递推式 T(n)=2T(n2)+O(1)T(n)=2T(\frac{n}{2})+O(1)T(n)=2T(2n)+O(1) 完美匹配主定理 的标准形式：
T(n)=aT(nb)+f(n)T(n) = aT(\frac{n}{b}) + f(n)T(n)=aT(bn)+f(n)

其中：a=2a=2a=2（子问题个数）、b=2b=2b=2（子问题规模缩小倍数）、f(n)=O(1)=n0f(n)=O(1)=n^0f(n)=O(1)=n0

主定理结论：若 log⁡ba>d\log_b a > dlogba>d（f(n)=ndf(n)=n^df(n)=nd），则 T(n)=O(nlog⁡ba)T(n)=O(n^{\log_b a})T(n)=O(nlogba)

本题中 log⁡22=1>0\log_2 2 = 1 > 0log22=1>0，因此直接得：
T(n)=O(n1)=O(n)T(n) = O(n^1) = O(n)T(n)=O(n1)=O(n)

---

五、避坑：排除其他错误选项的关键

1. ❌ O(n)O(\sqrt{n})O(n )：无任何递推规律支撑，本题和平方根无关；
2. ❌ O(2n)O(2^n)O(2n)：这是指数级递归 的复杂度（如 T(n)=2T(n−1)+O(1)T(n)=2T(n-1)+O(1)T(n)=2T(n−1)+O(1)，每次规模减1，调用2次），和本题「规模折半」完全不同；
3. ❌ O(log⁡2n)O(\log_2n)O(log2n)：这是单次递归 的复杂度（如 T(n)=T(n2)+O(1)T(n)=T(\frac{n}{2})+O(1)T(n)=T(2n)+O(1)，每次仅调用1次子问题），本题是2次子问题调用，复杂度更高。

---

✅ 最终答案

O(n)\boldsymbol{O(n)}O(n)，选择 A 选项。

例3（复杂算法）

✅ 本题答案：O(n)\boldsymbol{O(n)}O(n)，选择 A 选项

---

一、前置核心知识（2个必考点，本题全考）

1. 时间复杂度的计算原则

本题是单层分支+单层循环 结构，无嵌套循环、无递归，时间复杂度 = 代码中执行次数最多的那一段基本操作的次数 ，所有数组赋值/算术运算均为 O(1)\boldsymbol{O(1)}O(1) 的常数级基本操作。

2. 3个复杂度符号的精准含义（本题「隐藏核心考点」，90%的人忽略）

题干选项出现 O、Θ、Ω\boldsymbol{O、Θ、Ω}O、Θ、Ω 三种符号，必须分清才能避坑，这是本题的关键门槛：

• O(f(n))\boldsymbol{O(f(n))}O(f(n)) ：表示算法执行时间的 上界 → 「执行次数 ≤ C·f(n)」（C为常数），也是笔试最常考的「时间复杂度」默认定义；
• Ω(f(n))\boldsymbol{Ω(f(n))}Ω(f(n)) ：表示算法执行时间的 下界 → 「执行次数 ≥ C·f(n)」；
• Θ(f(n))\boldsymbol{Θ(f(n))}Θ(f(n)) ：表示算法执行时间的 紧确界 → 「下界=上界」，执行次数刚好是 f(n)f(n)f(n) 的常数倍，不多不少。

3. 题干已知条件

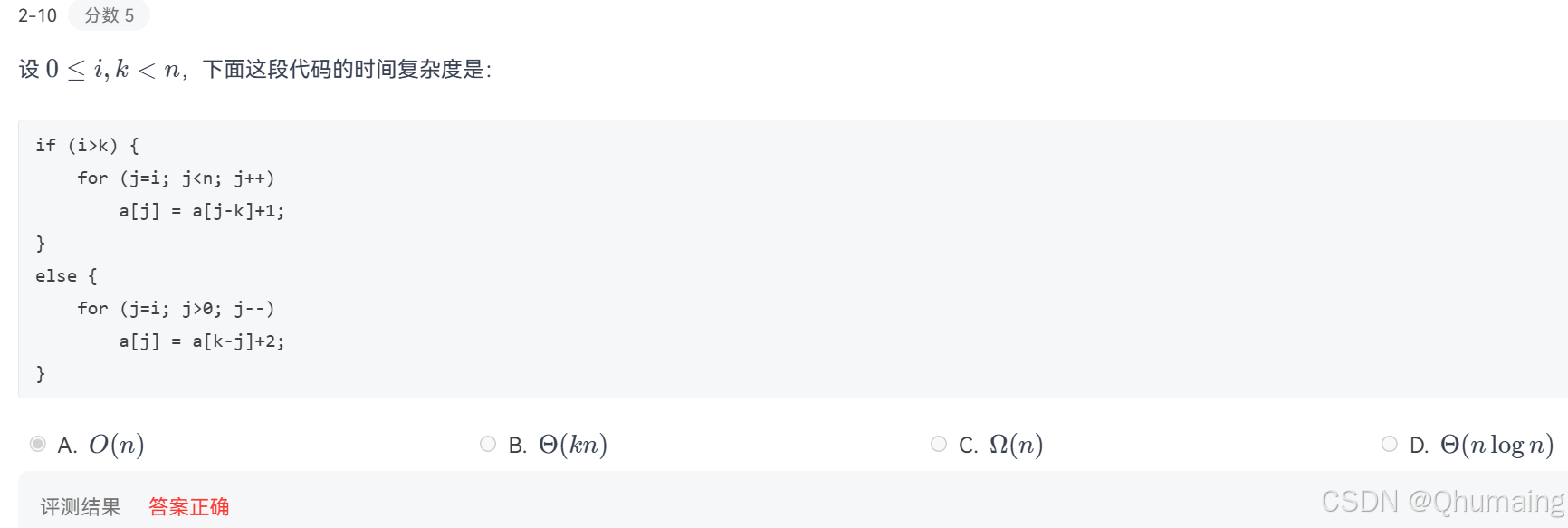
0≤i,k<n0 \le i,k < n0≤i,k<n ，i、ki、ki、k 都是固定的常数级参数 （是给定的取值，不是随n变化的变量），仅参与逻辑判断和数组下标计算，不影响循环的执行次数。

---

二、逐分支拆解循环执行次数（核心推导）

代码是if-else互斥分支，永远只会执行其中一个分支，我们分别计算两个分支的循环执行次数，取「最大值」作为整体时间复杂度即可。

if (i>k) {
    // 分支1：i>k时执行，单层for循环
    for (j=i; j<n; j++) a[j] = a[j-k]+1;
}
else {
    // 分支2：i≤k时执行，单层for循环
    for (j=i; j>0; j--) a[j] = a[k-j]+2;
}

✔️ 分支1：i>ki>ki>k 时，for(j=i; j<n; j++)

• 循环变量 jjj 起始值：iii ，终止条件：j<nj < nj<n ，步长：+1+1+1
• 循环执行次数 = n−i\boldsymbol{n - i}n−i
• 次数范围：0≤i<n0 \le i < n0≤i<n → 循环次数的最大值 = n （当 i=0i=0i=0 时）、最小值 = 111（当 i=n−1i=n-1i=n−1 时）
• 结论：分支1的时间开销 ≤n×O(1)=O(n)\le n \times O(1) = \boldsymbol{O(n)}≤n×O(1)=O(n)

✔️ 分支2：i≤ki≤ki≤k 时，for(j=i; j>0; j--)

• 循环变量 jjj 起始值：iii ，终止条件：j>0j > 0j>0 ，步长：−1-1−1
• 循环执行次数 = i\boldsymbol{i}i
• 次数范围：0≤i<n0 \le i < n0≤i<n → 循环次数的最大值 = n-1 （当 i=n−1i=n-1i=n−1 时）、最小值 = 000（当 i=0i=0i=0 时，循环不执行）
• 结论：分支2的时间开销 ≤(n−1)×O(1)=O(n)\le (n-1) \times O(1) = \boldsymbol{O(n)}≤(n−1)×O(1)=O(n)

---

三、关键易错点：为什么 k\boldsymbol{k}k 对复杂度无影响？

这是本题最大的坑 ，很多人会误选B选项 Θ(kn)\Theta(kn)Θ(kn)，原因是看到代码里有变量kkk就误以为是k×nk×nk×n的复杂度，这里给出铁律结论：

✅ kkk 是「固定参数」，仅出现在数组下标 中（j−k、k−jj-k、k-jj−k、k−j），只是做数组元素的寻址，这个寻址操作是 O(1)\boldsymbol{O(1)}O(1) 的常数级操作；

✅ 循环的执行次数只和i、ni、ni、n有关 ，和kkk没有任何关系，kkk不会增加循环的轮数，也不会在循环内嵌套新的循环；

✅ 只有当 kkk 是循环变量、或出现双层嵌套循环（比如for(k)套for(n)）时 ，才会出现knknkn的复杂度，本题完全不满足。

---

四、逐一排除错误选项（完整避坑，必看）

❌ B. Θ(kn)\boldsymbol{\Theta(kn)}Θ(kn)

1. kkk是固定参数，不是变量，循环次数与kkk无关，无knknkn的乘积关系；
2. Θ\ThetaΘ代表「紧确界」，要求执行次数的上下界一致，本题循环次数可多可少（0~n），不存在紧确界；
3. 即使kkk是变量，本题也无任何kkk相关的循环，纯干扰项。

❌ C. Ω(n)\boldsymbol{\Omega(n)}Ω(n)

Ω(n)\Omega(n)Ω(n) 表示「算法的执行次数至少 是nnn的常数倍」（下界为nnn），但本题中：

• 分支2当i=0i=0i=0时，循环执行0次；
• 分支1当i=n−1i=n-1i=n−1时，循环执行1次 ；
  显然执行次数「可以远小于n」，不满足「下界为n」的要求，直接排除。

❌ D. Θ(nlog⁡n)\boldsymbol{\Theta(n\log n)}Θ(nlogn)

对数阶复杂度（nlog⁡nn\log nnlogn）的出现场景是固定的：分治递归、折半查找、归并排序等，要求循环/递归中「规模折半/倍增」。本题是纯线性单层循环，无任何对数相关逻辑，纯干扰项。

---

五、最终结论推导

两个分支的循环执行次数的最大上限 都是 nnn 次，所有基本操作都是常数级 O(1)O(1)O(1)，根据时间复杂度「取上界、忽略常数」的原则：

该代码的时间复杂度 = O(n)\boldsymbol{O(n)}O(n)

---

✨ 同类题秒杀技巧（通用结论，背会直接做题）

1. 单层for循环（无嵌套），循环变量线性增减 → 时间复杂度必为 O(n)\boldsymbol{O(n)}O(n)；
2. 看到 Θ(kn)\Theta(kn)Θ(kn) 先排除，除非有双层嵌套循环；
3. 看到 Ω(f(n))\Omega(f(n))Ω(f(n)) 先判断：是否「无论输入如何，执行次数都不会低于f(n)f(n)f(n)」，否则排除；
4. 看到 Θ(nlog⁡n)\Theta(n\log n)Θ(nlogn) 先判断：是否有「折半/分治」逻辑，否则排除。

答案再确认：O(n)\boldsymbol{O(n)}O(n)，选择 A。

---

---

---

>> 求空间复杂度

例3（对比例1求斐波那契）

✅ 本题答案：O(log⁡2n)\boldsymbol{O(\log_2 n)}O(log2n)，选择 B 选项

---

一、核心前提：递归算法的空间复杂度核心考点

递归函数的空间复杂度，99%的场景下由「递归调用栈的深度」决定，这是解这类题的核心原则，必须牢记：

1. 函数内的局部变量（本题中int s）是常数级空间开销 O(1)O(1)O(1)，每次递归只会申请1个整型变量，且内存可复用，对整体复杂度无影响；
2. 递归调用时，程序会为每一层递归创建「栈帧」（存返回地址、参数、局部变量），栈帧的叠加层数 = 递归调用栈的深度，这是空间开销的主体；
3. 递归栈的特点：先进后出，内层递归执行完毕后，对应栈帧会立即释放，不会同时占用多层独立的大块内存。

---

二、分析本题的递归调用逻辑

函数 foo(n) 是单层递归调用，执行逻辑非常清晰：

int foo(int n)
{
    int s; // 仅申请1个整型变量，O(1)空间
    if (n <= 1) { s = 1; } // 递归终止条件：无新调用，栈深度不再增加
    else { s = foo(n / 2) * 2; } // 核心：只「单次调用」foo(n/2)，无并行递归
    return s;
}

✅ 关键区别：本题是 foo(n/2)*2 → 1次递归调用 ；上一题是 foo(n/2)+foo(n/2) → 2次递归调用，这是两道题的核心差异。

---

三、推导递归调用栈的深度（重中之重）

递归调用的过程是「层层深入，逐层返回」，函数的调用链路是单向链式调用，比如：

• 当 n=8n=8n=8 时，调用链路：foo(8)→foo(4)→foo(2)→foo(1)\boldsymbol{foo(8) → foo(4) → foo(2) → foo(1)}foo(8)→foo(4)→foo(2)→foo(1)
• 当 n=16n=16n=16 时，调用链路：foo(16)→foo(8)→foo(4)→foo(2)→foo(1)\boldsymbol{foo(16) → foo(8) → foo(4) → foo(2) → foo(1)}foo(16)→foo(8)→foo(4)→foo(2)→foo(1)
• 当 n=4n=4n=4 时，调用链路：foo(4)→foo(2)→foo(1)\boldsymbol{foo(4) → foo(2) → foo(1)}foo(4)→foo(2)→foo(1)

规律总结

每次递归调用，问题规模都会折半 （n→n/2n \rightarrow n/2n→n/2），直到触发终止条件 n≤1n \le 1n≤1 为止。

设递归调用栈的深度为 kkk，则满足：
n2k≤1  ⟹  2k≥n  ⟹  k=log⁡2n\frac{n}{2^k} \le 1 \implies 2^k \ge n \implies \boldsymbol{k = \log_2 n}2kn≤1⟹2k≥n⟹k=log2n

这意味着：递归调用栈的最大深度就是 log⁡2n\log_2 nlog2n 层，空间开销由这个深度决定。

---

四、最终空间复杂度结论

递归栈深度 = log⁡2n\log_2 nlog2n，每层栈帧的空间开销是常数级 O(1)O(1)O(1)，因此整体空间复杂度为：
S(n)=O(log⁡2n)\boldsymbol{S(n) = O(\log_2 n)}S(n)=O(log2n)

---

五、避坑：排除所有错误选项（必看）

❌ A. O(n)O(n)O(n)

这是线性递归 的空间复杂度，对应场景是「每次递归规模减1」，比如 foo(n) = foo(n-1)+1，调用链路是 foo(n)→foo(n−1)→...→foo(1)foo(n)→foo(n-1)→...→foo(1)foo(n)→foo(n−1)→...→foo(1)，栈深度为 nnn，本题是规模折半，不是减1。

❌ C. O(n2)O(n^2)O(n2)

平方级空间复杂度，通常对应「二维数组、双层嵌套递归申请内存」等场景，本题无任何嵌套内存申请，和 n2n^2n2 完全无关，纯干扰项。

❌ D. O(2n)O(2^n)O(2n)

指数级空间复杂度，对应「指数级递归调用栈」，比如斐波那契递归 fib(n)=fib(n-1)+fib(n-2)，本题是规模折半的单次递归，复杂度天差地别。

---

六、补充：本题的「时间复杂度」顺带推导（同考点，必掌握）

顺带求一下这个函数的时间复杂度，加深理解，逻辑一致：

设时间复杂度为 T(n)T(n)T(n)，递推公式为：
{T(n)=O(1)n≤1T(n)=T(n2)+O(1)n>1 \begin{cases} T(n) = O(1) \quad &n \le 1 \\ T(n) = T(\frac{n}{2}) + O(1) \quad &n > 1 \end{cases} {T(n)=O(1)T(n)=T(2n)+O(1)n≤1n>1

时间开销的次数 = 递归调用的次数 = 递归栈的深度 = log⁡2n\log_2 nlog2n，因此时间复杂度也是 O(log⁡2n)\boldsymbol{O(\log_2 n)}O(log2n)。

---

✨ 同类题核心记忆（秒杀技巧）

针对「规模折半的递归函数」，总结万能结论，以后直接套用：

1. 单次递归调用：foo(n) = foo(n/2) + 常数 → 时间/空间复杂度均为 O(log⁡2n)\boldsymbol{O(\log_2 n)}O(log2n)；
2. 两次递归调用：foo(n) = foo(n/2)+foo(n/2) + 常数 → 时间复杂度 O(n)\boldsymbol{O(n)}O(n)，空间复杂度依然 O(log⁡2n)\boldsymbol{O(\log_2 n)}O(log2n)（空间只看栈深度）。

例4（阶乘计算）

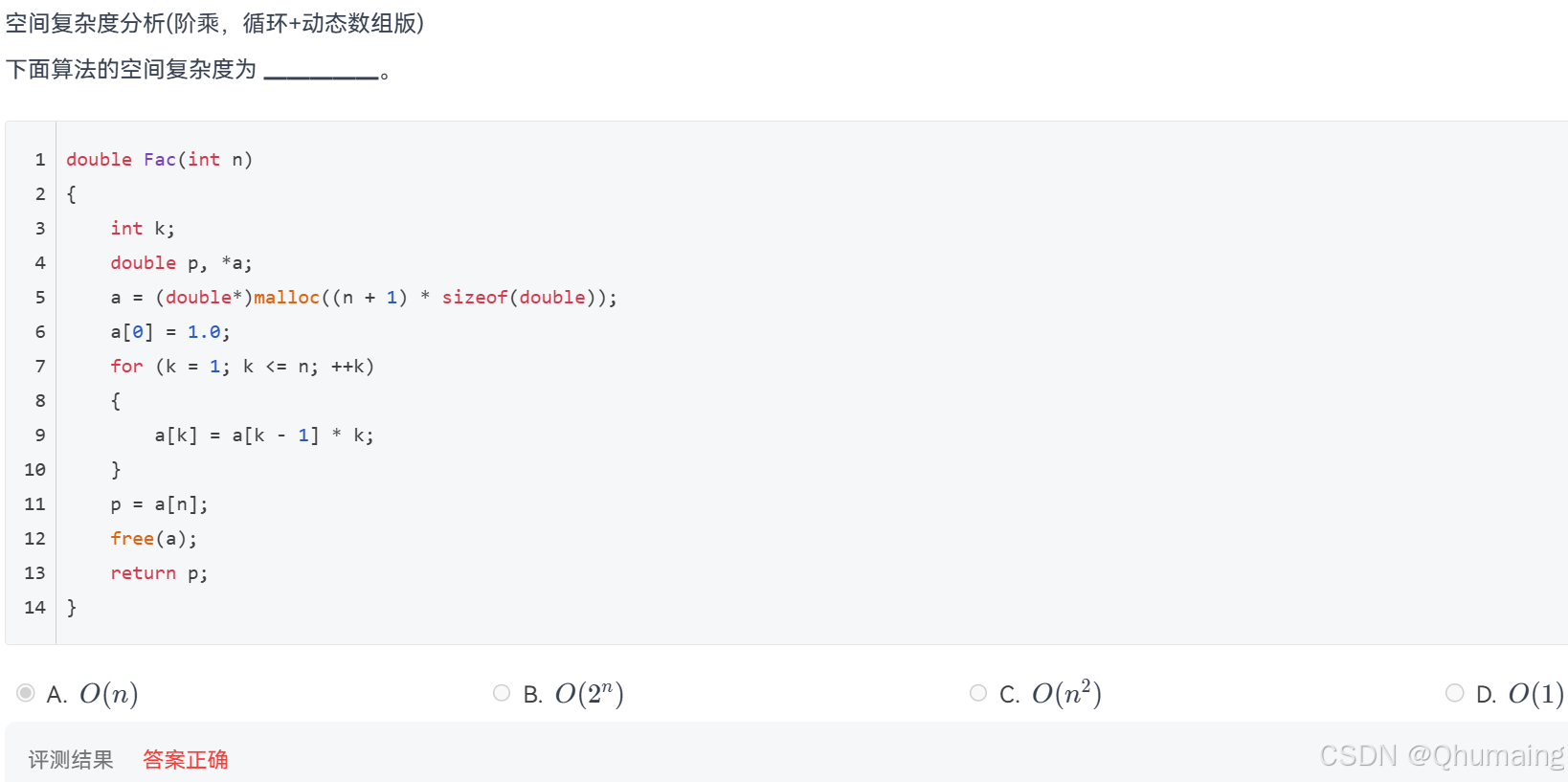
✅ 本题答案：O(n)\boldsymbol{O(n)}O(n)，选择 A 选项

---

一、核心前提：「非递归算法」空间复杂度的分析原则

本题是纯循环+动态内存申请 的非递归代码，无任何递归调用，和之前的递归栈深度分析完全不同，核心原则：

非递归算法的空间复杂度 = 「固定局部变量的常数空间」 + 「动态申请内存/容器的可变空间」

复杂度取「最高阶项」，忽略常数、忽略低阶项（空间复杂度的通用规则）

---

二、逐行拆解代码的「空间占用」细节

double Fac(int n)
{
    int k;          // 固定局部变量：整型，占常数空间 O(1)
    double p, *a;   // 固定局部变量：浮点型+指针，占常数空间 O(1)
    // 【核心开销】动态申请内存，这是本题的关键！
    a = (double*)malloc((n + 1) * sizeof(double));
    a[0] = 1.0;
    for (k = 1; k <= n; ++k) { a[k] = a[k - 1] * k; }
    p = a[n];
    free(a);        // 释放内存，不影响空间复杂度计算！
    return p;
}

关键细节说明（必考考点）

1. 固定局部变量的空间 ：k、p、a 都是「单个变量」，无论输入的 nnn 是多大，这类变量的数量是固定不变 的，所有单个变量的空间开销统一记为 O(1)\boldsymbol{O(1)}O(1)（常数级）；
2. 动态申请的内存空间 ：malloc((n+1)*sizeof(double)) 是本题的唯一可变空间开销 ：
   • 申请了连续的 n+1n+1n+1 个 double 类型的内存单元；
   • 内存占用的「大小」和输入规模 nnn 成正比；
3. free的作用 ：free(a) 只是释放申请的内存，避免内存泄漏。但空间复杂度计算的是「程序运行过程中占用的最大空间」，不是最终是否释放，所以这行代码对复杂度无影响。

---

三、严谨推导空间复杂度

动态申请的内存大小为：(n+1)×sizeof(double)(n+1) \times sizeof(double)(n+1)×sizeof(double)

• sizeof(double)sizeof(double)sizeof(double)：是一个固定常数（8字节），空间复杂度中忽略常数系数；
• n+1n+1n+1：是关于 nnn 的一次项，空间复杂度中忽略低阶项（常数项1）；

因此，动态申请的空间复杂度为 O(n)O(n)O(n)，加上固定变量的 O(1)O(1)O(1)，整体空间复杂度遵循「取高阶项」原则：
S(n)=O(n)+O(1)=O(n) S(n) = O(n) + O(1) = \boldsymbol{O(n)} S(n)=O(n)+O(1)=O(n)

---

四、避坑：逐一排除错误选项（必考易错点）

❌ B. O(2n)O(2^n)O(2n) 指数级

指数级空间复杂度，通常对应「递归生成所有子集/排列」「动态申请指数级内存」等极端场景，本题仅申请线性内存，和指数无关，纯干扰项。

❌ C. O(n2)O(n^2)O(n2) 平方级

平方级空间复杂度，对应「二维数组/二维动态内存」（比如 malloc(n*n*sizeof(double))），本题是一维动态数组，仅线性空间，无平方关系。

❌ D. O(1)O(1)O(1) 常数级（高频易错选项，重中之重）

O(1)O(1)O(1) 是本题的最大陷阱！这里必须做一个黄金对比，帮你彻底分清：

✅ 什么情况下阶乘的空间复杂度是 O(1)\boldsymbol{O(1)}O(1)？

如果我们不用数组，只用一个变量累乘实现阶乘：

double Fac(int n){
    double res = 1.0;
    for(int k=1;k<=n;k++) res *=k;
    return res;
}

这种写法无动态内存申请 ，只有固定局部变量，空间复杂度才是 O(1)O(1)O(1)。
❌ 本题为什么不是 O(1)O(1)O(1)？

因为本题额外申请了长度为 n+1n+1n+1 的动态数组 ，数组的空间随 nnn 增大而线性增大，这是「可变空间」，区别于常数空间。

---

🌟 补充：同类题「秒杀」结论（记熟直接做题）

针对「循环+数组/动态内存」的非递归算法，空间复杂度的通用结论：

1. 申请一维数组 （大小为 nnn）→ 空间复杂度 O(n)\boldsymbol{O(n)}O(n)；
2. 申请二维数组 （大小为 n×nn \times nn×n）→ 空间复杂度 O(n2)\boldsymbol{O(n^2)}O(n2)；
3. 无数组/动态内存，仅用变量运算 → 空间复杂度 O(1)\boldsymbol{O(1)}O(1)；

---

✨ 总结本题考点

本题的考点是「区分常数空间 和线性空间 」，核心是识别动态内存申请的语句，这是这类题的破题点，记住：

看到 malloc(n) / 数组大小和n相关 → 优先考虑 O(n)O(n)O(n)；

看到无动态内存、仅变量运算 → 一定是 O(1)O(1)O(1)。

最终答案再确认：O(n)\boldsymbol{O(n)}O(n)，选 A。

例5（对比例4阶乘）

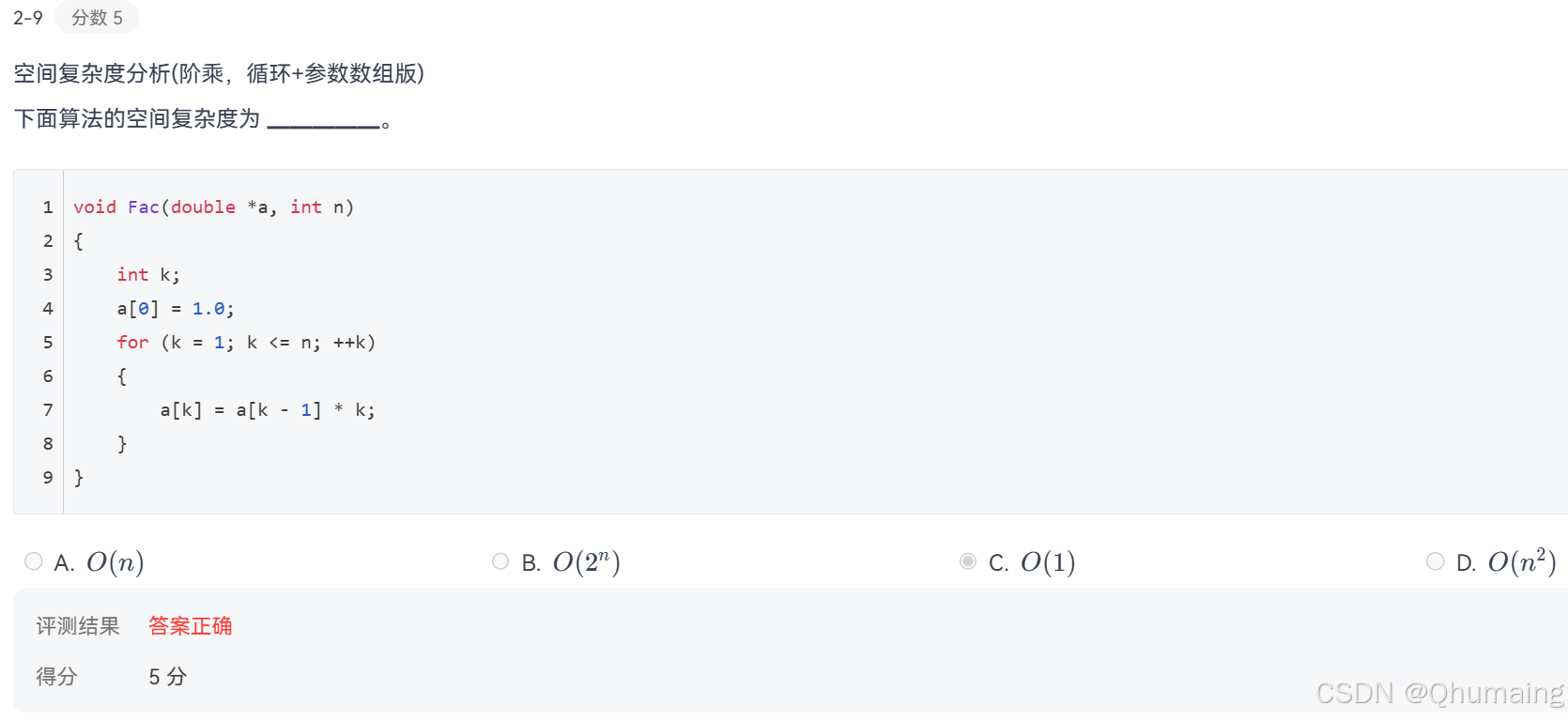
✅ 本题答案：O(1)\boldsymbol{O(1)}O(1)，选择 C 选项

---

🔥 本题核心考点（【最高频易错点】必背，和上一题形成黄金对比）

计算一个函数的空间复杂度，遵循铁律：

仅统计「当前函数内部主动开辟/申请 的额外内存空间」，函数调用时传入的参数（数组、指针、变量） ，其内存空间是在「调用方（主调函数）」中开辟的，不计入当前函数的空间复杂度！

✅ 这是本题和上一题「动态数组版阶乘」的唯一、本质区别，也是出题人设的最大陷阱！

---

一、逐行拆解代码的「空间占用」细节

void Fac(double *a, int n)
{
    int k;          // 仅1个局部整型变量，常数级空间 O(1)
    a[0] = 1.0;
    for (k = 1; k <= n; ++k) {
        a[k] = a[k - 1] * k;  // 仅对传入数组的元素赋值，无任何内存申请
    }
}

关键细节逐一解析（每题必考）

1. 关于参数 double *a ：
   a 是一个指针变量，它指向的数组内存，是调用这个 Fac 函数的地方提前开辟好的 （比如主函数里定义double arr[100];，再调用Fac(arr,99)）。这个数组的内存开销，算在「调用方」头上，和当前的Fac函数无关。

   而指针变量a本身，只是一个4/8字节的地址变量，属于「常数级空间」。

2. 关于局部变量 ：

   函数内只有 int k 这1个局部变量，无论输入的 nnn 多大，局部变量的数量固定、占用空间固定 ，是标准的 O(1)O(1)O(1) 常数级开销。

3. 关于循环操作 ：

   循环中只是做「数组元素赋值+乘法运算」，没有任何 malloc/calloc 动态内存申请，也没有创建新的数组/容器，无任何额外空间开销。

---

二、严谨推导空间复杂度

当前函数 Fac 的空间开销组成：
总空间=局部变量的常数空间+函数内部申请的额外空间\text{总空间} = \text{局部变量的常数空间} + \text{函数内部申请的额外空间}总空间=局部变量的常数空间+函数内部申请的额外空间

代入实际情况：
总空间=O(1)+O(0)=O(1)\text{总空间} = O(1) + O(0) = \boldsymbol{O(1)}总空间=O(1)+O(0)=O(1)

核心结论 ：这个函数执行过程中，占用的内存空间是固定不变的 ，不会随着输入规模 nnn 的增大而增大！

---

三、两道「阶乘题」生死对比（背会直接秒杀同类型题，必考）

这两道题题干几乎一样，答案完全不同，是考试最常考的同考点变式题，务必吃透区别，这是送分题也是丢分题：

✔️ 题1（动态数组版）：double Fac(int n)

a = (double*)malloc((n+1)*sizeof(double)); // 函数「内部」malloc申请n+1的数组

✅ 空间复杂度：O(n)\boldsymbol{O(n)}O(n)

✅ 原因：数组内存是当前函数主动开辟 的，空间大小和 nnn 成正比。

✔️ 题2（参数数组版）：void Fac(double *a, int n)

无malloc，数组是「外部传入」的

✅ 空间复杂度：O(1)\boldsymbol{O(1)}O(1)

✅ 原因：数组内存是调用方开辟的，当前函数只使用，不申请任何额外可变空间。

---

四、逐一排除错误选项（避坑必看）

❌ A. O(n)O(n)O(n) 线性级（最大陷阱，90%的人易错）

选择这个选项的同学，都是犯了「看到数组是n大小就选O(n)」的错误，忽略了数组的内存归属问题 。记住：不是有数组就是O(n)，要看数组是谁开辟的。

❌ B. O(2n)O(2^n)O(2n) 指数级

纯干扰项，指数级空间复杂度只会出现在「生成所有子集/排列」「递归开辟指数级内存」等极端场景，本题无任何指数相关逻辑。

❌ D. O(n2)O(n^2)O(n2) 平方级

纯干扰项，平方级空间复杂度对应「二维数组/二维动态内存」，本题连一维数组都没开辟，和平方无关。

---

✨ 补充：通用秒杀结论（记熟，所有空间复杂度题通用）

1. 函数参数传入数组/指针 → 该数组空间不计入当前函数空间复杂度；
2. 函数内部 malloc/calloc 申请数组 → 申请的数组空间计入当前函数空间复杂度；
3. 函数内只有「单个变量+循环」，无内存申请 → 空间复杂度必为 O(1)\boldsymbol{O(1)}O(1)；
4. 递归函数看「递归栈深度」，非递归函数看「内部申请的可变内存」。

---

最终答案再确认：O(1)\boldsymbol{O(1)}O(1)，选 C。