参考书目：
目录
第一章：python入门
用到的外部库：numpy，matplotlib
省略
第二章：感知机
运行原理，θ是阈值
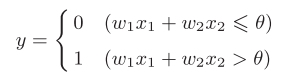
采用感知机实现逻辑门电路
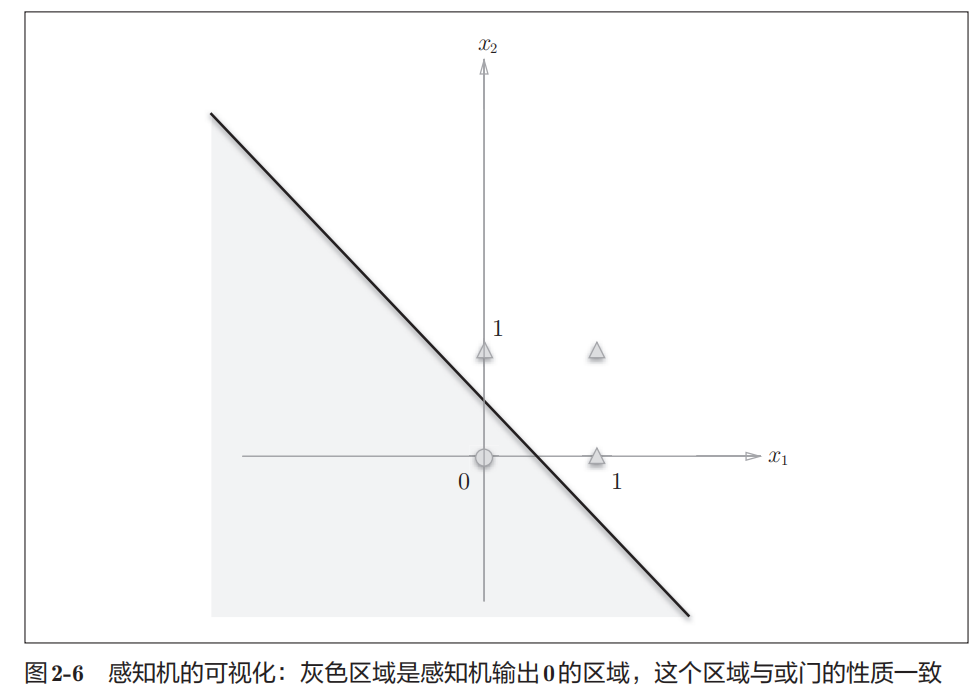
实现逻辑门电路相当于划线分割，将不同的类别区分开，这就是阈值的设定。
导入权重和偏置，令θ = -b，b为偏置，w1，w2是权重
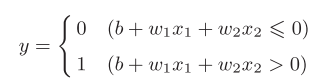
但是感知机存在局限性，在实现异或门的时候，无法一条直线区分开，如图
但是使用曲线可以分开
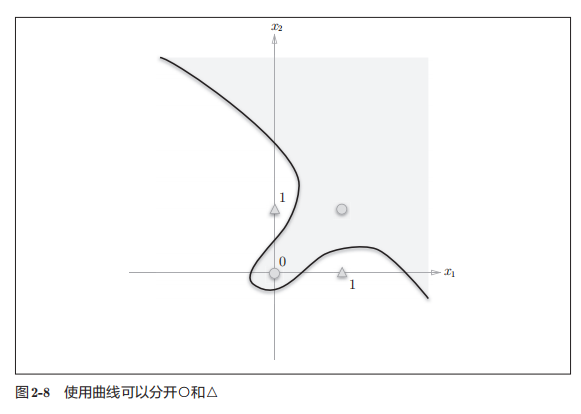
涉及到了线性和非线性的问题。
多层感知机
感知机可以叠加，2层感知机，因为只有两层之间存在权重
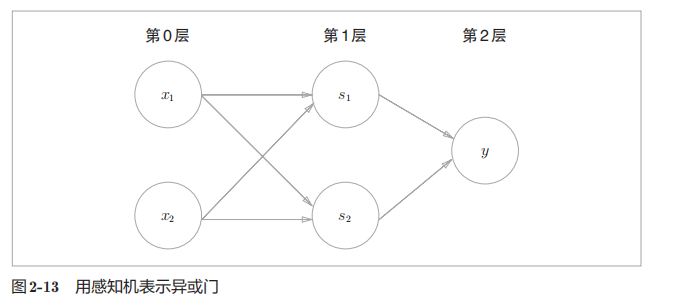
感知机通过叠加层可以进行非线性的表示，理论上还可以表示计算机进行的处理
第三章：神经网络
神经网络有输入层，中间层，输出层 。中间层有时也称为隐藏层。
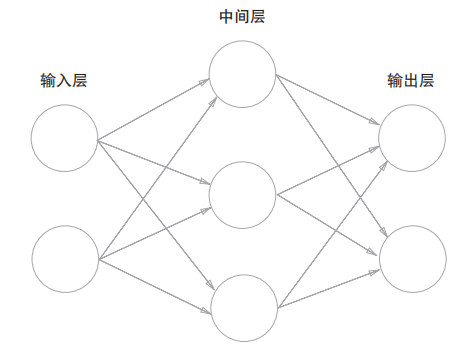
就神经元连接的方式，和感知机没什么区别，神经网络中信号是如何传递的呢？
我们将感知机的形式用函数来表示：
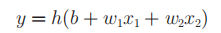
引入函数h（x），输入信号的总和会被h（x）转换
明确表示出偏置
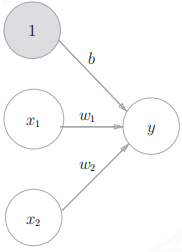
激活函数
阶跃函数
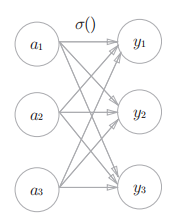
刚才登场的h（x）函数会将输人信号的总和转换为输出信号，这种函数一般称为激活函数（activationfunction）。如"激活"一词所示，激活函数的作用在于决定如何来激活输人信号的总和。
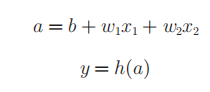
先计算输入信号的加权总和，然后用激活函数转换。
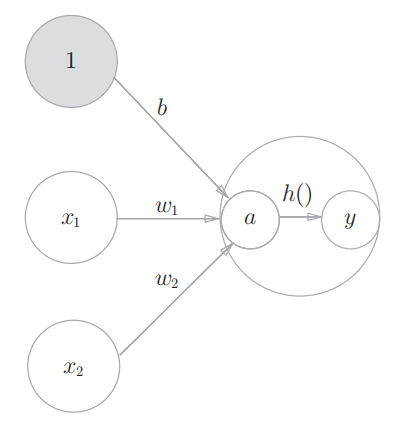
如图所示，表示神经元的○中明确显示了激活函数的计算过程，即信号的加权总和为节点a，然后节点a被激活函数h（转换成节点y。本书中，"神经元"和"节点"两个术语的含义相同。这里，我们称a和y为"节点"，其实它和之前所说的"神经元"含义相同。
以上激活函数以间值为界，一旦输人超过间值，就切换输出。这样的函数称为"阶跃函数"。因此，可以说感知机中使用了阶跃函数作为激活函数。也就是说，在激活函数的众多候选函数中，感知机使用了阶跃函数。那么，如果感知机使用其他函数作为激活函数的话会怎么样呢？实际上，如果将激活函数从阶跃函数换成其他函数，就可以进人神经网络的世界了。下面我们就来介绍一下神经网络使用的激活函数。
sigmoid函数
形式如下：
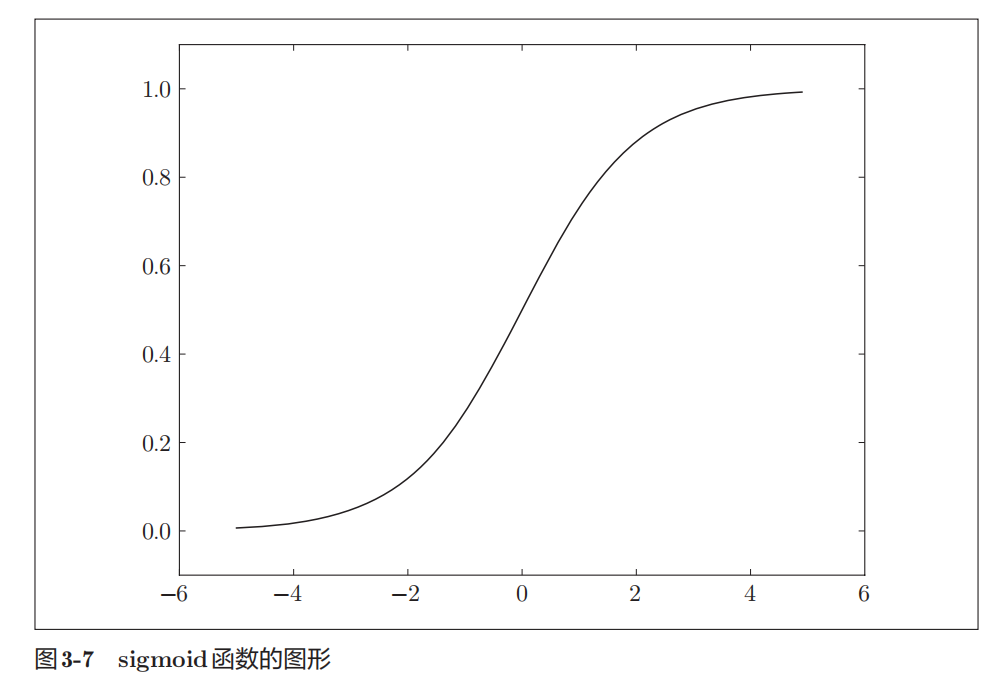
sigmoid函数的平滑性对神经网络有着重要意义。
阶跃函数和sigmoid函数，二者均为非线性函数。神经网络的激活函数必须使用非线性函数，因为如果是线性函数，那么加深神经网络的层数就没有意义了，都可以的等效成无隐藏层的网络。
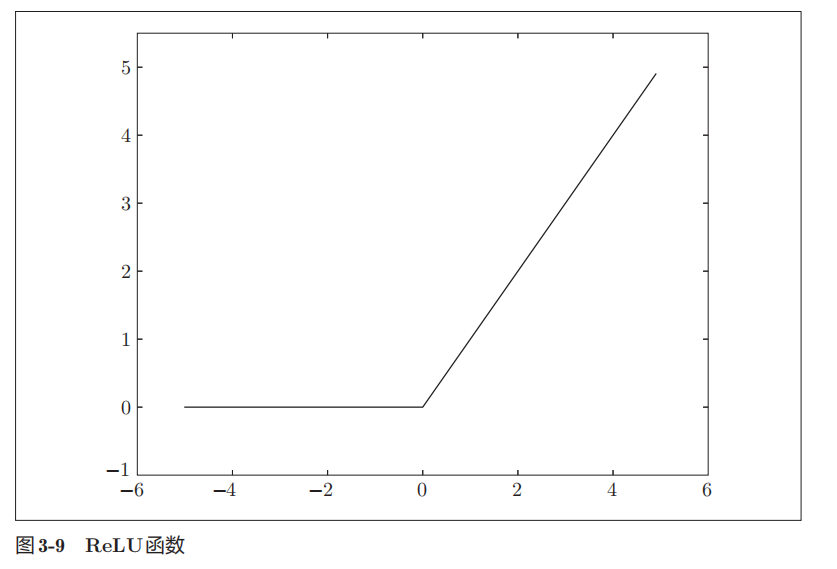
ReLU函数
ReLU（Rectified Linear Unit）函数，在输入大于0时，直接输出该值，输入小于零时，输出0
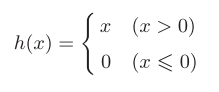
符号的确认
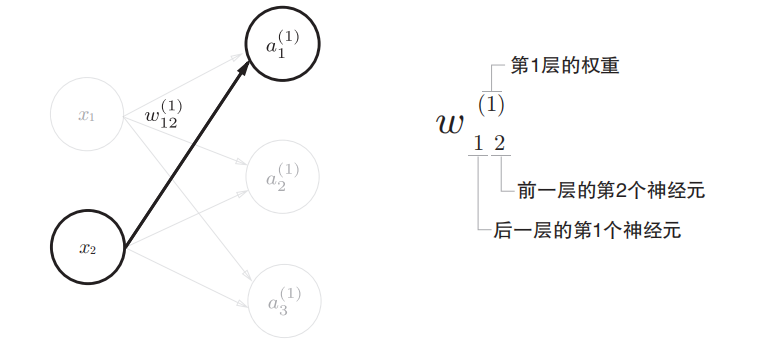
不同层之间的信号传递
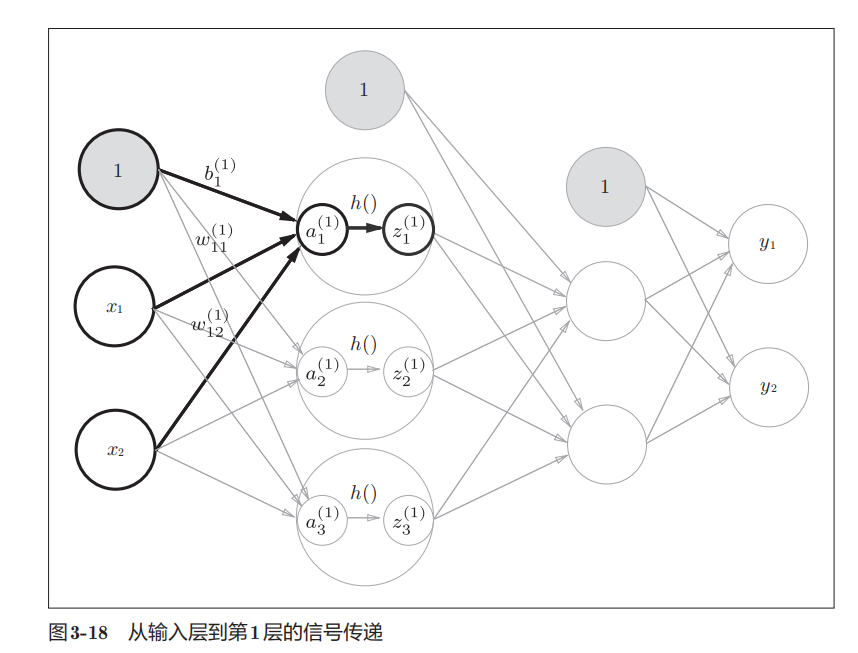
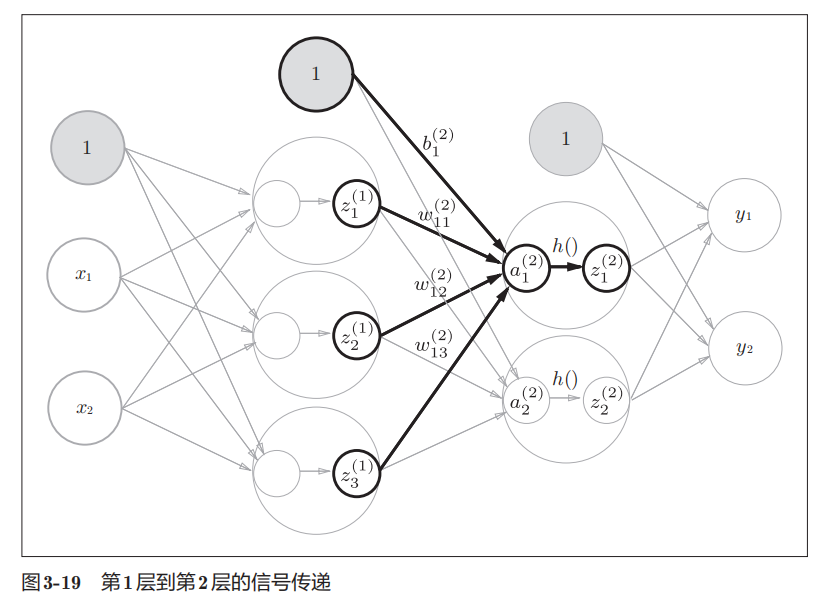
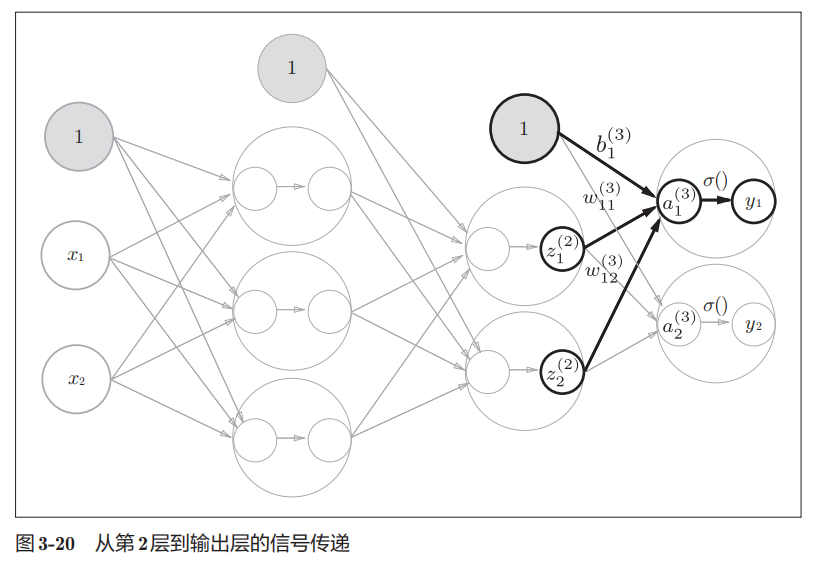
输出层的设计
神经网络可以用在分类和回归问题上，具体需要改变输出层的激活函数。一般来说，回归问题用恒等函数，分类问题用softmax函数。
|-----------|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 恒等函数 |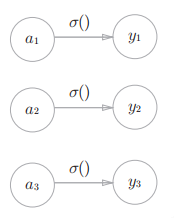 
|
| softmax函数 |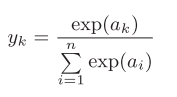 
指数函数的计算往往会导致值过大，可以做如下改进 
在进行softmax的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的C'可以使用任何值，但是为了防止溢出，一般会使用输人信号中的最大值。我们来看一个具体的例子。 |
**softmax函数的特征：**输出在0-1之间，而且输出的总和是1，这是很重要的一个特征，正是因为这个特征，我们才可以把输出的结果解释为概率。
输出层的神经元数量需要由待解决的问题决定。
手写数字识别
和求解机器学习问题的步骤（分成学习和推理两个阶段进行）一样，使用神经网络解决问题时，也需要首先使用训练数据（学习数据）进行权重参数的学习；进行推理时，使用刚才学习到的参数，对输入数据进行分类。
介绍完神经网络的结构之后，现在我们来试着解决实际问题。这里我们来进行手写数字图像的分类。假设学习已经全部结束，我们使用学习到的参数，先实现神经网络的"推理处理"。这个推理处理也称为神经网络的前向传播（forwardpropagation) 。
输入数据的集合称为批（batch）。通过以批为单位进行推理处理，能够实现高速的运算。
手写数字项目各大平台都有开源，采用minist数据集，大家可以自行复现。
第四章：神经网络的学习
从数据中学习
神经网络的特征就是可以从数据中学习。所谓"从数据中学习"，是指可以由数据自动决定权重参数的值。数据是机器学习的核心。
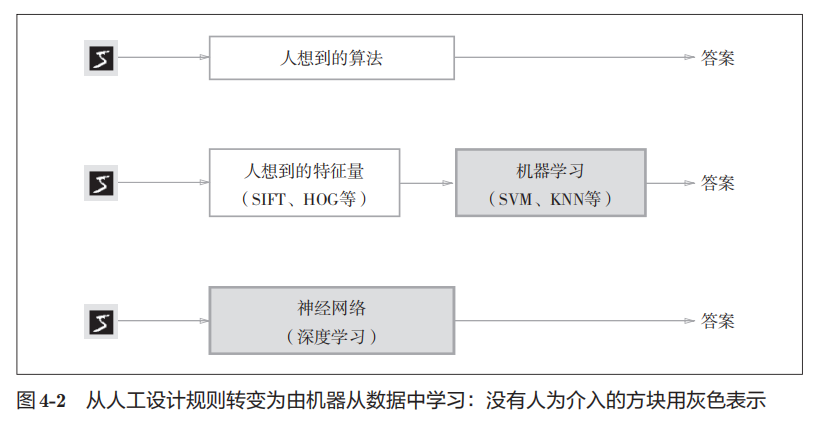
机器学习中，一般将数据分为训练数据和测试数据两部分来进行学习和实验等。首先，使用训练数据进行学习，寻找最优的参数；然后，使用测试数据评价训练得到的模型的实际能力。为什么需要将数据分为训练数据和测试数据呢？因为我们追求的是模型的泛化能力。为了正确评价模型的泛化能力，就必须划分训练数据和测试数据。另外，训练数据也可以称为监督数据。
泛化能力 是指处理未被观察过的数据（不包含在训练数据中的数据）的能力。只对某个数据集过度拟合的状态称为过拟合（overfitting）。避免过拟合也是机器学习的一个重要课题。
损失函数
神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数（lossfunction）。这个损失函数可以使用任意函数，但一般用均方误差和交叉误差等。
损失函数是表示神经网络性能的"恶劣程度"的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。以"性能的恶劣程度"为指标可能会使人感到不太自然，但是如果给损失函数乘上一个负值，就可以解释为"在多大程度上不坏"，即"性能有多好"。并且，"使性能的恶劣程度达到最小"和"使性能的优良程度达到最大"是等价的，不管是用"恶劣程度"还是"优良程度"，做的事情本质上都是一样的。
|-------|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 损失函数 | 公式 |
| 均方误差 |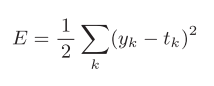 
表示神经网络的输出，
表示监督数据，k表示数据的维度 |
| 交叉熵误差 | 除了均方误差之外，交叉熵误差（crossentropyerror）也经被用作损失函数。交叉熵误差如下式所示。 
|
将正确标签表示为1，其他表示为0的方式称为one-hot表示。
mini-batch学习
如果要求所有数据损失函数的总和，可以写成如下方式，假设数据有N个，以交叉熵为例
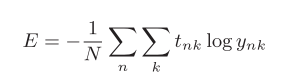
另外，MINIST数据集的训练数据有60000个，如果以全部数据为对象求损失函数的和，则计算过程需要花费较长的时间。再者，如果遇到大数据，数据量会有几百万、几千万之多，这种情况下以全部数据为对象计算损失函数是不现实的。因此，我们从全部数据中选出一部分，作为全部数据的"近似"。神经网络的学习也是从训练数据中选出一批数据（称为mini-batch，小批量 ），然后对每个mini-batch进行学习。比如，从60000个训练数据中随机选择100笔，再用这100笔数据进行学习。这种学习方式称为mini-batch学习。
寻找最优参数（权重和偏置）时，要寻找使损失函数的值尽可能小的参数，需要计算参数的导数（梯度），然后以这个导数为指引，逐步更新参数的值。
在进行神经网络的学习时，不能将识别精度作为指标。因为如果以识别精度为指标，则参数的导数在绝大多数地方都会变为0。
sigmoid函数的斜率不为0，而阶跃函数大多数地方为0，因此如果使用阶跃函数为激活函数，即便使用损失函数作为指标，参数的微小变化也会被抹杀，导致学习无法进行。
数值微分
先介绍一下导数，导数就是某个瞬间的变化量
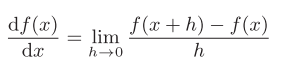
**中心差分：**以x为中心，计算x+h和x-h的差分
**前向差分：**x+h和x之间的差分
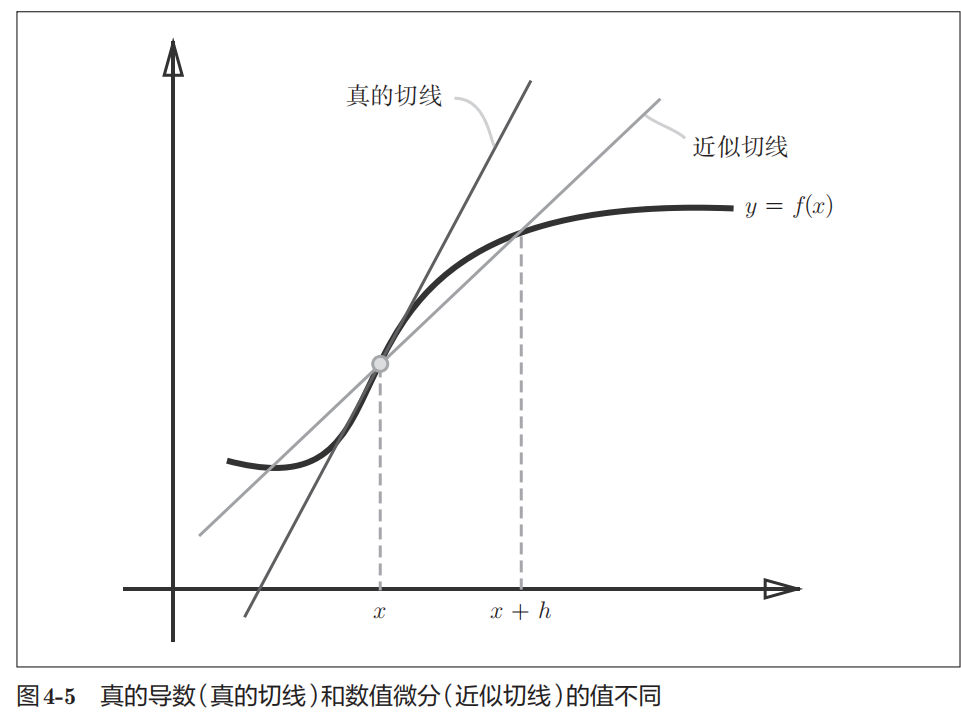
所谓数值微分（numerial differentiation），就是用数值方法近似求解函数导数的过程
偏导数：有多个变量的函数的导数
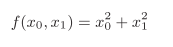
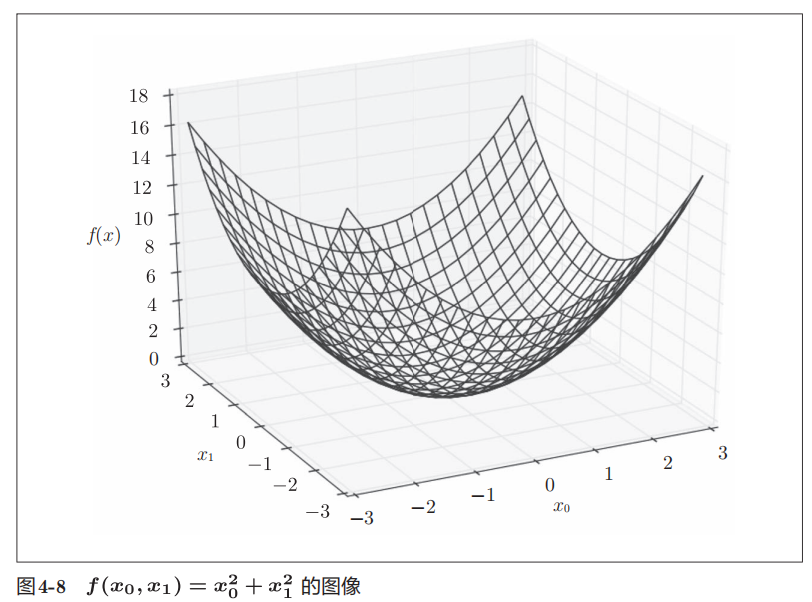
梯度：由全部变量的偏导数汇总而成的向量
以刚才的函数为例，我们发现梯度呈现为有向向量（箭头）。同时梯度指向函数最低处（最小值），所有箭头都指向同一点，并且离最低处越远，箭头越大。
虽然梯度指向了最低处，但并非任何时候都这样。实际上，梯度会指向各点处的函数值降低的方向。更严格地讲，梯度指示的方向是各点处的函数值减小最多的方向。这是一个非常重要的性质，请一定牢记！
梯度法
机器学习的主要任务是在学习时寻找最优参数。同样地，神经网络也必须在学习时找到最优参数（权重和偏置）。这里所说的最优参数是指损失函数取最小值时的参数。但是，一般而言，损失函数很复杂，参数空间庞大，我们不知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值 （或者尽可能小的值）的方法就是梯度法。
这里需要注意的是，梯度表示的是各点处的函数值减小最多的方向。因此，无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上，在复杂的函数中，梯度指示的方向基本上都不是函数值最小处。
函数的极小值、最小值以及被称为**鞍点（saddlepoint）**的地方，梯度为0。极小值是局部最小值，也就是限定在某个范围内的最小值。**鞍点是从某个方向上看是极大值，从另一个方向上看则是极小值的点。**虽然梯度法是要寻找梯度为0的地方，但是那个地方不一定就是最小值（也有可能是极小值或者鞍点）。此外，当函数很复杂且呈扁平状时，学习可能会进入一个（几乎）平坦的地区，陷入被称为"学习高原"的无法前进的停滞期。
在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进，如此反复，不断地沿梯度方向前进。像这样，通过不断地沿梯度方向前进，逐渐减小函数值的过程就是 梯度法（gradientmethod）。梯度法是解决机器学习中最优化问题的常用方法，特别是在神经网络的学习中经常被使用。
根据目的是寻找最小值还是最大值，梯度法的叫法有所不同。严格地讲，寻找最小值的梯度法称为梯度下降法（gradientdescentmethod） ，寻找最大值的梯度法称为梯度上升法（gradientascentmethod） 。但是通过反转损失函数的符号，求最小值的问题和求最大值的问题会变成相同的问题，因此"下降"还是"上升"的差异本质上并不重要。一般来说，神经网络（深度学习）中，梯度法主要是指梯度下降法。
尝试用数学来表示梯度法：
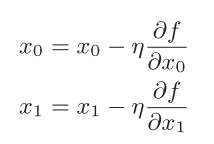
η表示更新量，在神经网络的的学习中，称为学习率（learning rate）。学习率决定在一次学习中，该学习多少，以及在多大程度上更新参数。学习率需要事先确定为某个值，比如0.01或0.001。一般而言，这个值过大或过小，都无法抵达一个"好的位置"。在神经网络的学习中，一般会一边改变学习率的值，一边确认学习是否正确进行了。
实验结果表明，学习率过大的话，会发散成一个很大的值；反过来，学习率过小的话，基本上没怎么更新就结束了。也就是说，设定合适的学习率是一个很重要的问题。
像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的，学习率这样的超参数则是人工设定的。一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。
神经网络的梯度可以表示为如下，以形状为2×3的权重W的神经网络
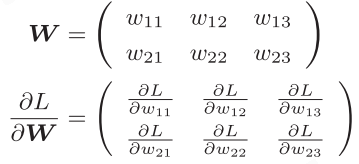
学习算法的实现
前提：神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为"学习"。神经网络的学习分成下面4个步骤：
- 步骤1（mini-batch）：从训练数据中随机选出一部分数据，这部分数据称为mini-batch。我们的目标是减小mini-batch的损失函数的值。
- 步骤2（计算梯度）：为了减小mini-batch的损失函数的值，需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。
- 步骤3（更新参数）：将权重参数沿梯度方向进行微小更新。
- 步骤4（重复）：重复步骤1、步骤2、步骤3。
神经网络的学习按照上面4个步骤进行。这个方法通过梯度下降法更新参数，不过因为这里使用的数据是随机选择的minibatch数据，所以又称为随机梯度下降法 （stochasticgradientdescent）。"随机"指的是"随机选择的"的意思，因此，随机梯度下降法是"对随机选择的数据进行的梯度下降法"。深度学习的很多框架中，随机梯度下降法一般由一个名为SGD 的函数来实现。SGD来源于随机梯度下降法的英文名称的首字母。
第五章：误差反向传播法
理解误差的反向传播有两种方式，一种是基于数学式，另一种是基于计算图。
计算图
**计算图：**计算图将计算过程用图形表示出来。这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为"边"）。
计算图的举例，买苹果
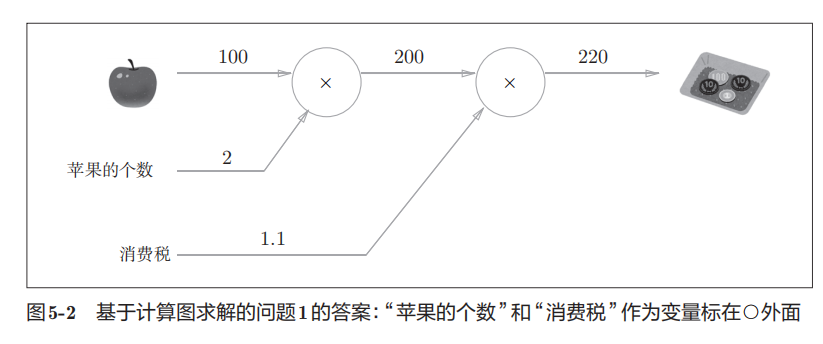
计算图的流程
- 1.构建计算图
- 2.在计算图上从左向右进行计算
这里的第2步是一种正方向上的传播，简称为正向传播（forwardpropagation）。正向传播是从计算图出发点到结束点的传播。既然有正向传播这个名称，当然也可以考虑反向（从图上看的话，就是从右向左）的传播。实际上，这种传播称为反向传播（backwardpropagation）。反向传播将在接下来的导数计算中发挥重要作用。
计算图的特征是可以通过传递**"局部计算"** 获得最终结果。"局部"这个词的意思是"与自己相关的某个小范围"。局部计算是指，无论全局发生了什么，都能只根据与自己相关的信息输出接下来的结果。
我们用一个具体的例子来说明局部计算。比如，在超市买了2个苹果和其他很多东西。此时，可以画出如图所示的计算图。
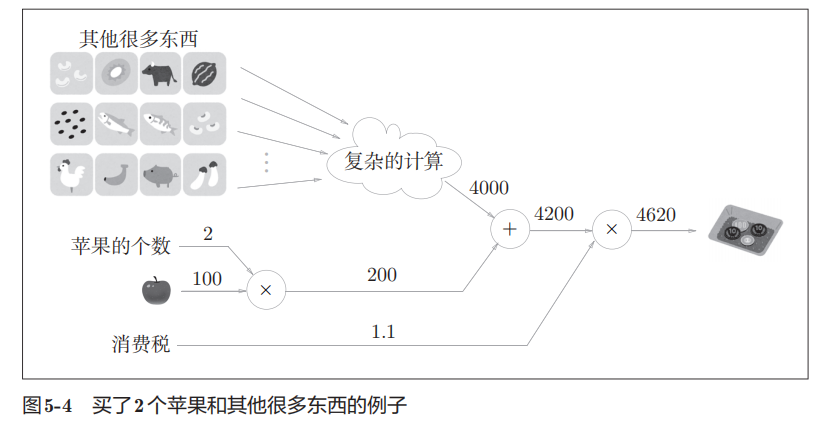
计算图的优点：
- 局部计算
- 可以将中间的计算结果保存
- 可以通过反向传播高效计算导数
看一下反向传播
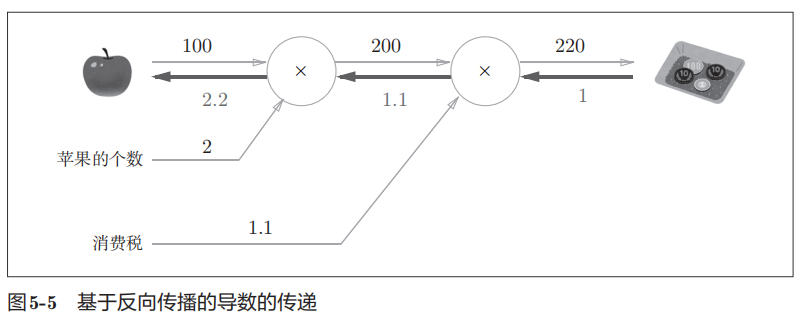
反向传播传递局部导数，这个例子当中可以知道支付金额关于苹果价格的导数是2.2。也就是苹果价格上涨一个微小的数值，最终支付金额会上涨这个微小数值的2.2倍。
这里只求了关于苹果的价格的导数，不过"支付金额关于消费税的导数""支付金额关于苹果的个数的导数"等也都可以用同样的方式算出来。并且，计算中途求得的导数的结果（中间传递的导数）可以被共享，从而可以高效地计算多个导数。综上，计算图的优点是，可以通过正向传播和反向传
播高效地计算各个变量的导数值。
链式法则
传递局部导数的原理，是基于链式法则（chain rule）
链式法则：如果某个函数由复合函数表示，则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。
计算图反向传播的例子：
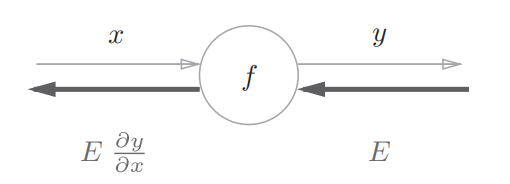
用计算图表示链式法则
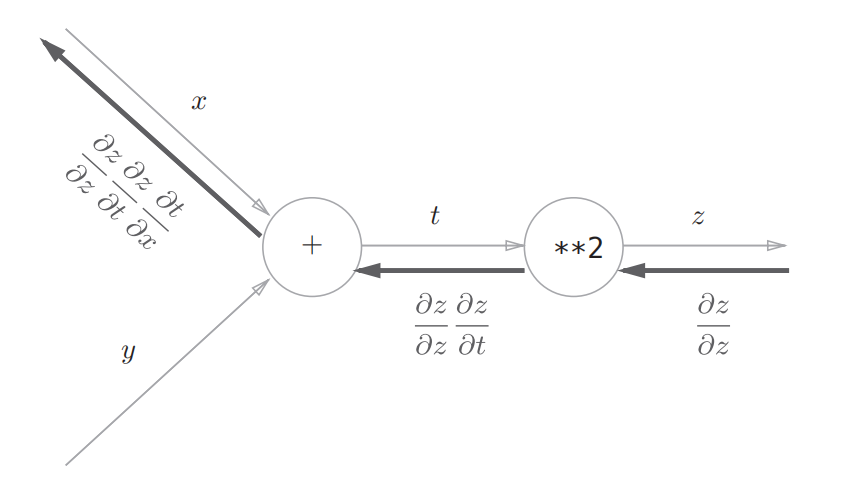
反向传播对于不同计算节点
|------|----------------------------------------------------------------------------------------------------------------------------------------------------------|
| 加法节点 |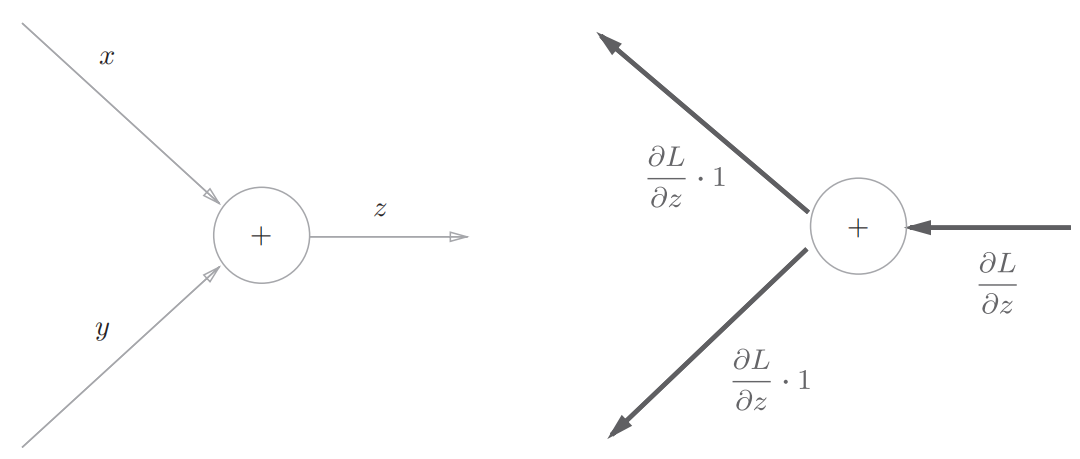 
举例：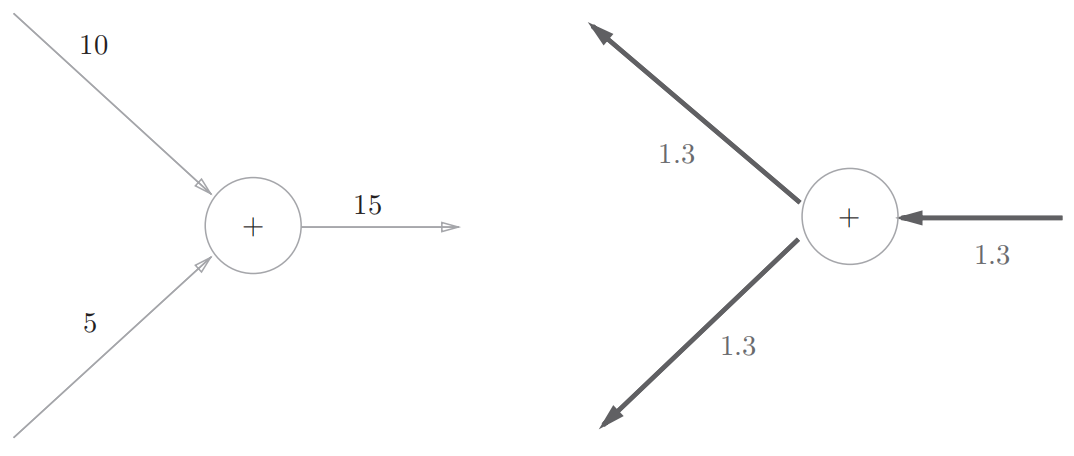 
|
| 乘法节点 |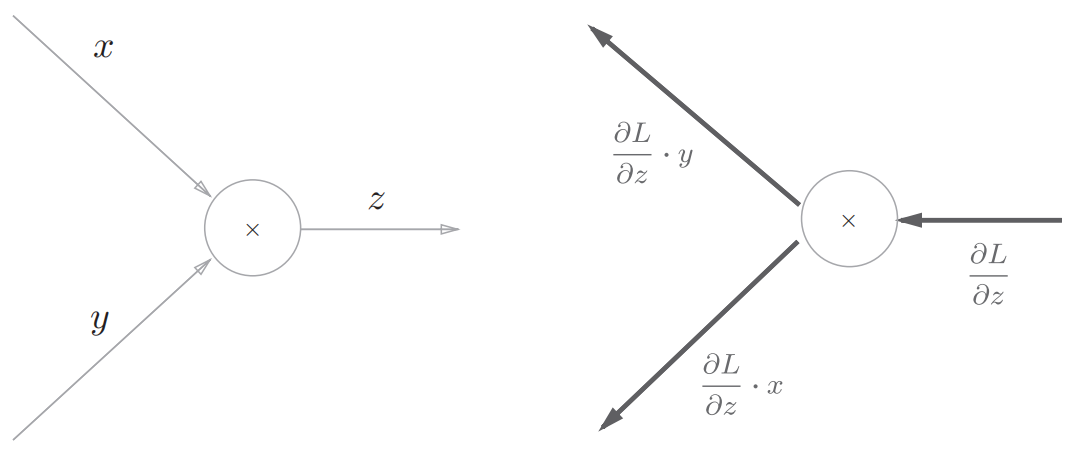 
举例： 
|
简单层的实现
本节将用Python实现前面的购买苹果的例子。这里，我们把要实现的计算图的乘法节点称为"乘法层"（MuLLayer），加法节点称为"加法层"(AddLayer)。
激活函数层的实现
ReLU层
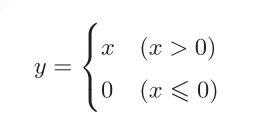
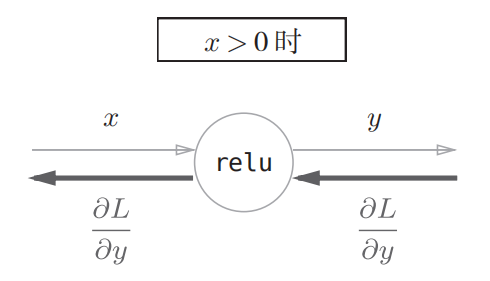
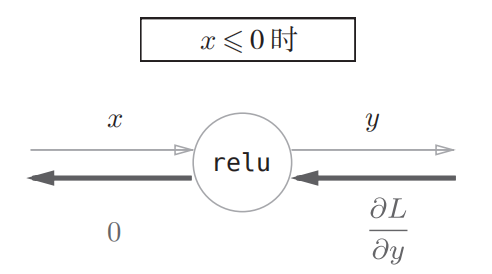
可以求出y关于x的导数
|----------------------------------------------------------------------------|----------------------------------------------------------------------------|
| 
| 
|
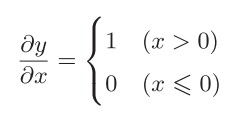
ReLU层的作用就像电路中的开关一样。正向传播时，有电流通过的话，就将开关设为ON：没有电流通过的话，就将开关设为OFF。反向传播时，开关为ON的话，电流会直接通过；开关为OFF的话，则不会有电流通过。
Sigmoid层
函数如下：
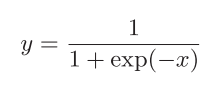
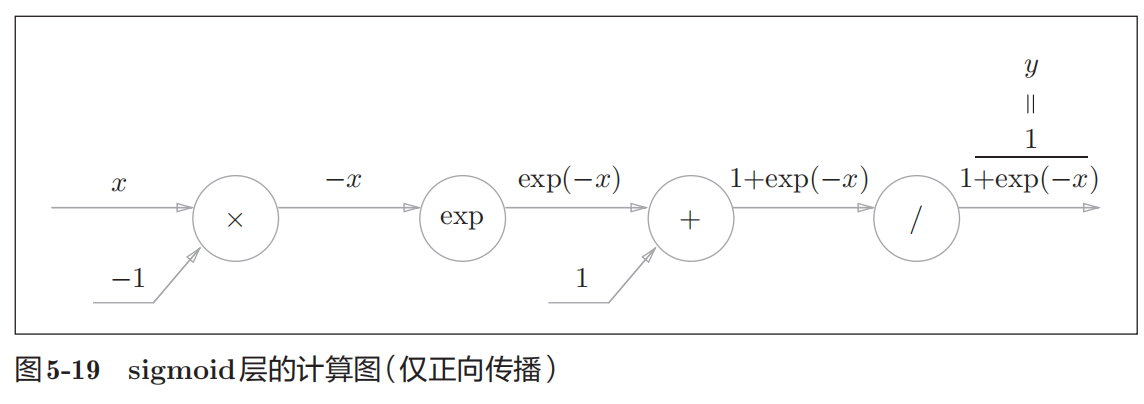
一步步计算反向传播
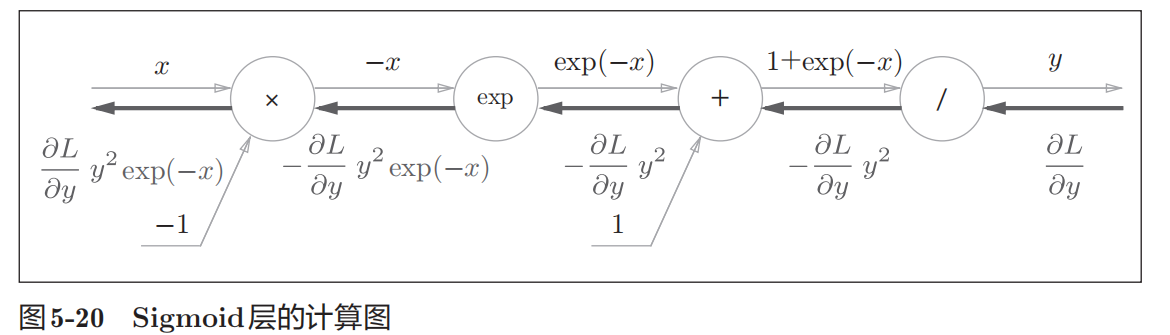
最终简化版
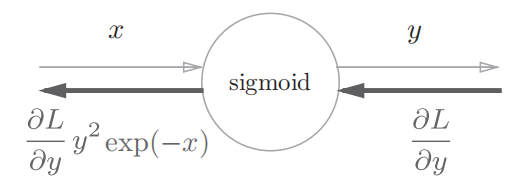
反向传播的值根据正向传播输入的x和y就能够算出来
Affine/Softmax层
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为**"仿射变换"**。因此，这里将进行仿射变换的处理实现为"Affine层"。
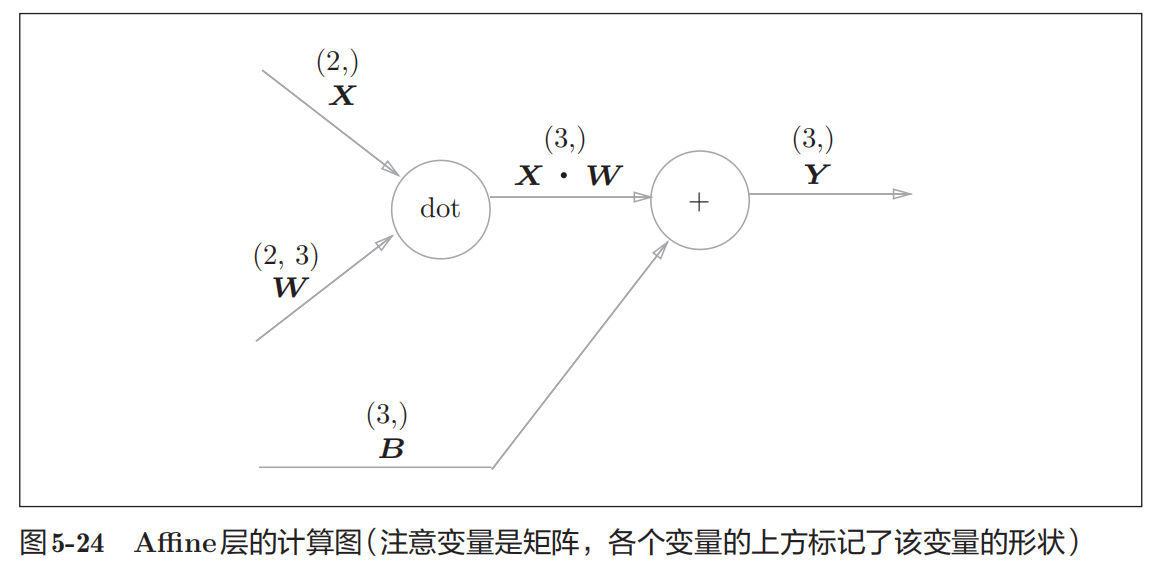
之前见到的计算图各个节点流动的是标量，而这里节点间传播的是矩阵，计算反向传播
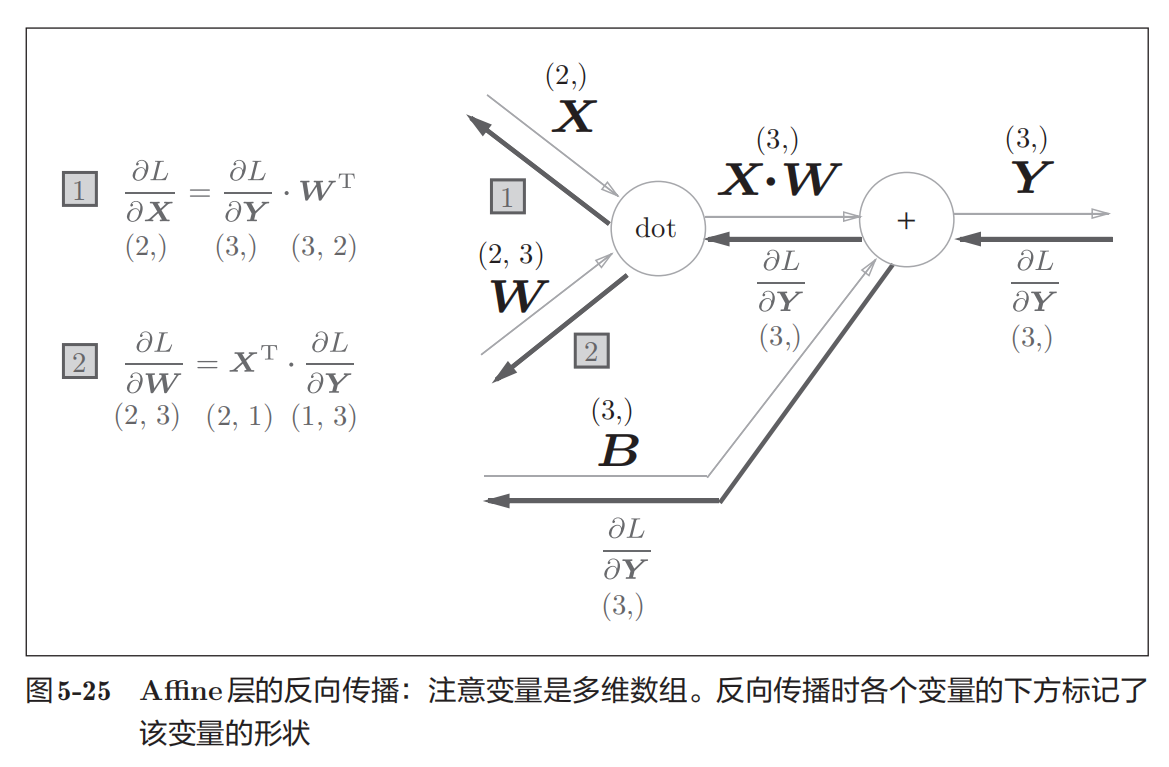
Softmax-with-Loss层
最后介绍一下输出层的softmax函数。前面我们提到过，softmax函数会将输入值正规化之后再输出。比如手写数字识别时，Sofmax层的输出如图所示。
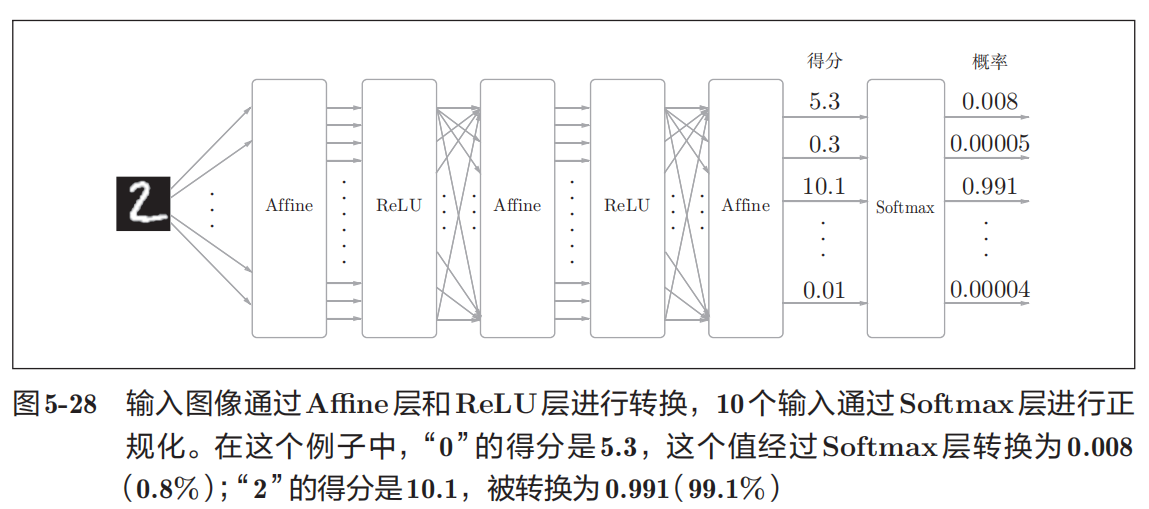
神经网络中进行的处理有推理（inference）和学习两个阶段。神经网络的推理通常不使用Softmax层。比如，用图5-28的网络进行推理时，会将最后一个Affine层的输出作为识别结果。神经网络中未被正规化的输出结果（图5-28中Softmax层前面的Affine层的输出）有时
被称为"得分"。也就是说，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要Softmax层。不过，神经网络的学习阶段则需要Softmax层。
误差反向传播的实现
神经网络学习的全貌图
前提：神经网络中有合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为学习。神经网络的学习分为下面4个步骤。
- 步骤1（mini-batch）：从训练数据中随机选择一部分数据。
- 步骤2（计算梯度）：计算损失函数关于各个权重参数的梯度。
- 步骤3（更新参数）：将权重参数沿梯度方向进行微小的更新。
- 步骤4（重复）：重复步骤1、步骤2、步骤3。
像这样通过将神经网络的组成元素以层的方式实现，可以轻松地构建神经网络。这个用层进行模块化的实现具有很大优点。因为想另外构建一个神经网络（比如5层、10层、20层·............的大的神经网络）时，只需像组装乐高积木那样添加必要的层就可以了。之后，通过各个层内部实现的正向传播和反向传播，就可以正确计算进行识别处理或学习所需的梯度 。
**梯度确认（gradient check）：**确认数值微分求出的结果和误差反向传播的结果是否一致。
和以前一样，读人MINIST数据集。然后，使用训练数据的一部分，确认数值微分求出的梯度和误差反向传播法求出的梯度的误差。这里误差的计算方法是求各个权重参数中对应元素的差的绝对值，并计算其平均值。如下：
第六章：和学习相关的技巧
本章将介绍神经网络的学习中的一些重要观点，主题涉及寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法 等。此外，为了应对过拟合 ，本章还将介绍权值衰减、Dropout等正则化方法， 并进行实现。最后将对近年来众多研究中使用的BatchNormalization方法进行简单的介绍。使用本章介绍的方法，可以高效地进行神经网络（深度学习）的学习，提高识别精度。
参数的更新
神经网络的学习的目的是找到使损失函数的值尽可能小的参数。这是寻找最优参数的问题，解决这个问题的过程称为最优化（optimization） 。遗憾的是，神经网络的最优化问题非常难。这是因为参数空间非常复杂，无法轻易找到最优解（无法使用那种通过解数学式一下子就求得最小值的方法）。而且，在深度神经网络中，参数的数量非常庞大，导致最优化问题更加复杂。
在前几章中，为了找到最优参数，我们将参数的梯度（导数） 作为了线索。使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降法（stochastic gradient descent），简称SGD 。SGD是一个简单的方法，不过比起胡乱地搜索参数空间，也算是"聪明"的方法。但是，根据不同的问题，也存在比SGD更加聪明的方法。
SGD可以写成如下形式
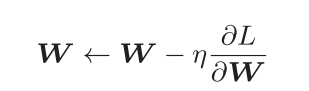
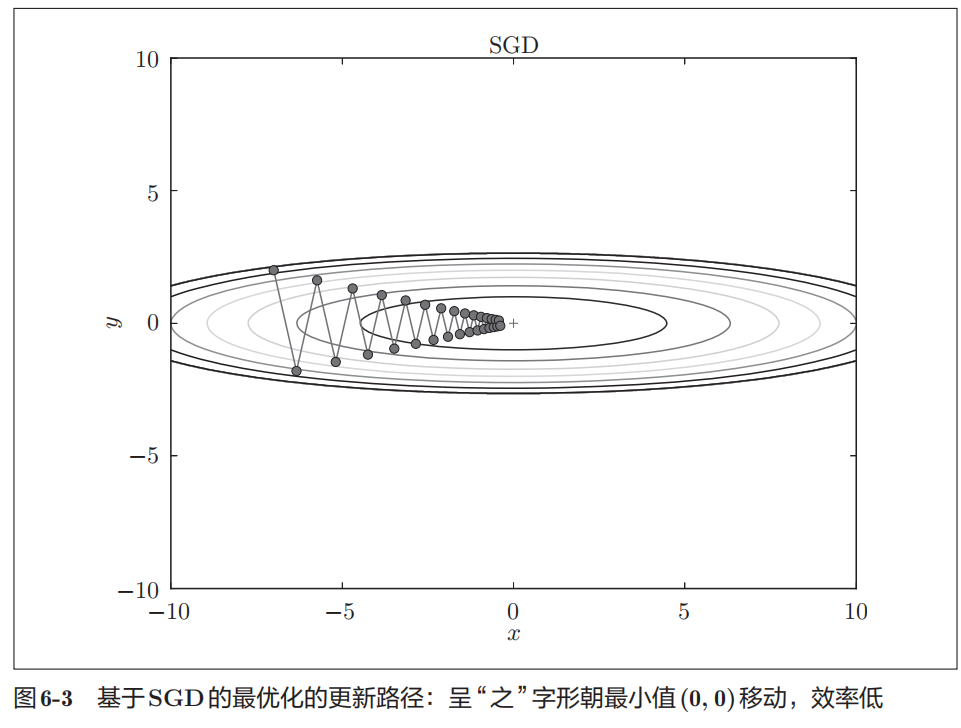
SGD低效的根本原因是，梯度方向并没有指向最小值的方向，有时候需要呈之字形移动，这是相当低效的方法，下面会介绍三种方法来取代：Momentum，AdaGrad，Adam
Momentum
Momentum是动量的意思，和物理有关，用数学的方式表示如下：
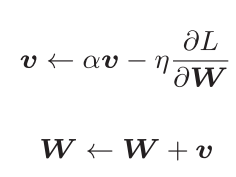
这里新出现了一个变量v，对应物理上的速度。第一个式子表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则。Momentum方法给人的感觉就像是小球在地面上滚动。
更新路径是这样的，之字形程度减弱
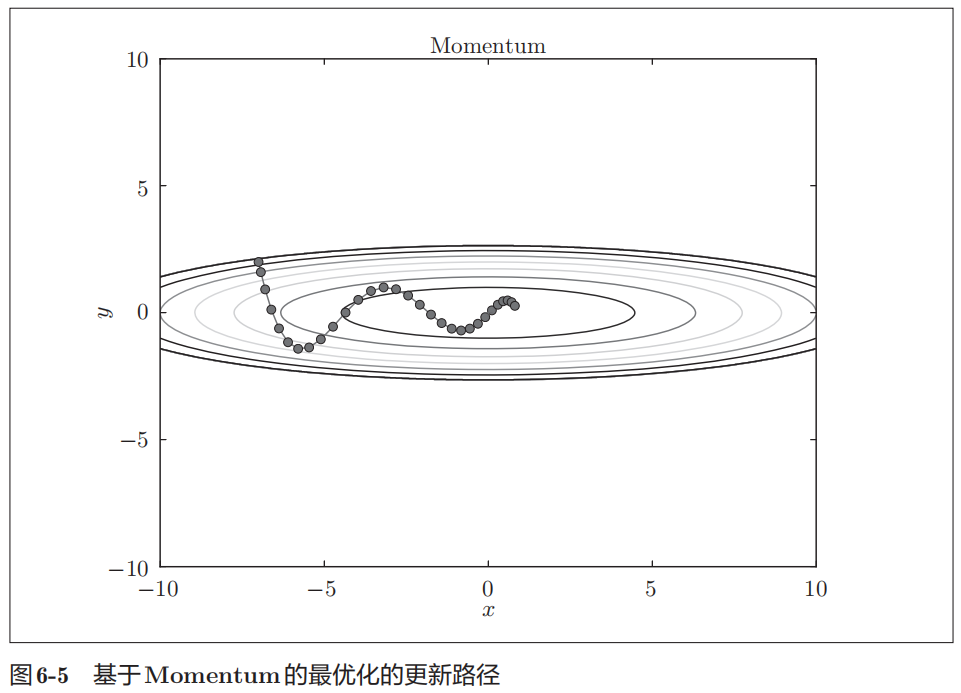
AdaGrad
在神经网络的学习中，学习率 （数学式中记为η）的值很重要。学习率过小，会导致学习花费过多时间；反过来，学习率过大，则会导致学习发散而不能正确进行。
在关于学习率的有效技巧中，有一种被称为学习率衰减（learningratedecay） 的方法，即随着学习的进行，使学习率逐渐减小。实际上，一开始"多"学，然后逐渐"少"学的方法，在神经网络的学习中经常被使用。逐渐减小学习率的想法，相当于将"全体"参数的学习率值一起降低。AdaGrad进一步发展了这个想法，针对"一个一个"的参数，赋予其"定制"的值。
AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习（AdaGrad的Ada来自英文单词Adaptive，即"适当的"的意思）。下面，让我们用数学式表示AdaGrad的更新方法。
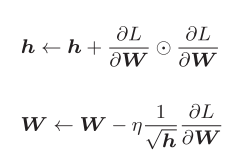
这里新出现了变量h ，它保存了以前的所有梯度值的平方和中的圆圈符号表示对应矩阵元素的乘法。然后，在更新参数时，通过乘以，就可以调整学习的尺度。这意味着，参数的元素中变动较大（被大幅更新）的元素的学习率将变小。也就是说，可以按参数的元素进行学习率衰减，使变动大的参数的学习率逐渐减小。
AdaGrad会记录过去所有梯度的平方和。因此，学习越深入，更新的幅度就越小。实际上，如果无止境地学习，更新量就会变为0，完全不再更新。为了改善这个问题，可以使用RMSProp方法。RMSProp 方法并不是将过去所有的梯度一视同仁地相加，而是逐渐地遗忘过去的梯度，在做加法运算时将新梯度的信息更多地反映出来。这种操作从专业上讲，称为**"指数移动平均"**，呈指数函数式地减小过去的梯度的尺度。
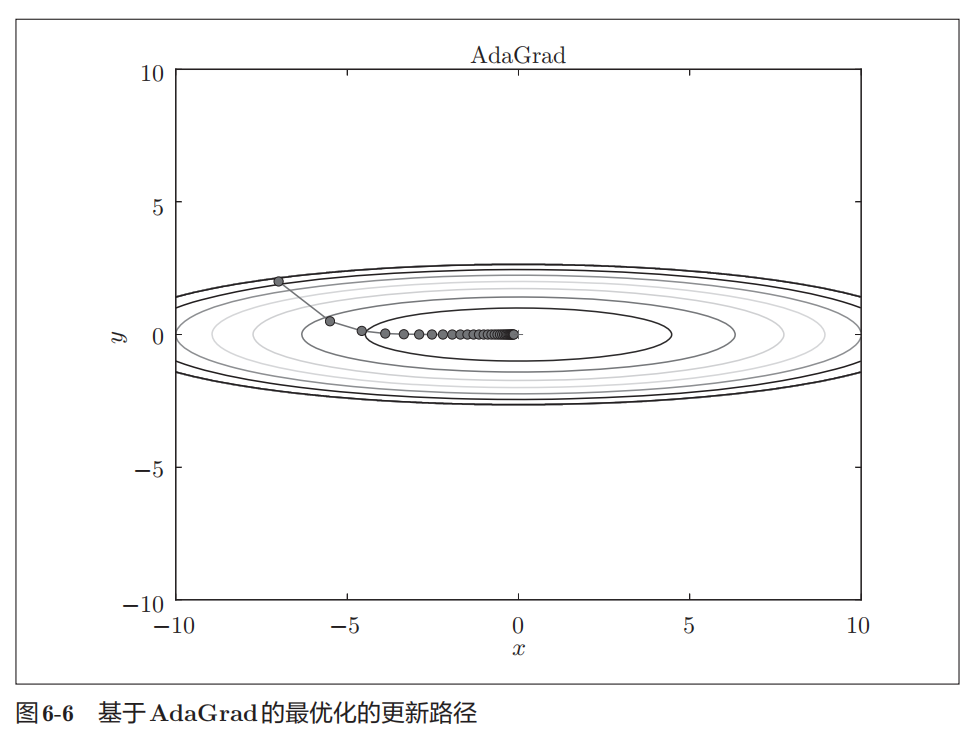
由图的结果可知，函数的取值高效地向着最小值移动。由于y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，"之"字形的变动程度有所衰减。
Adam
Momentum参照小球在碗中滚动的物理规则进行移动，AdaGrad为参数的每个元素适当地调整更新步伐。如果将这两个方法融合在一起会怎么样呢？这就是Adam方法的基本思路
Adam是2015年提出的新方法。它的理论有些复杂，直观地讲，就是融合了Momentum和AdaGrad的方法 。通过组合前面两个方法的优点，有望实现参数空间的高效搜索。此外，进行超参数的"偏置校正" 也是Adam的特征。这里不再进行过多的说明，详细内容请参考原作者的论文。
最优化的更新路径如下
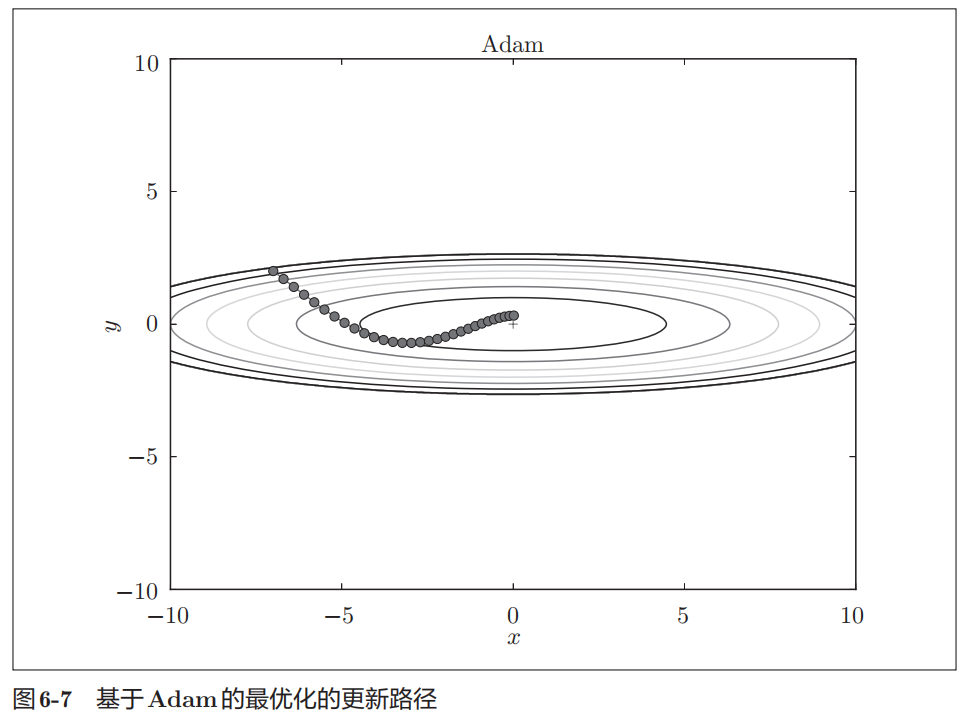
Adam会设置3个超参数。一个是学习率（论文中以α出现），另外两个是一次momentum系数β1和二次momentum系数β2。根据论文，标准的设定值是β1为0.9，β2为0.999。设置了这些值后，大多数情况下都能顺利运行。
权重的初始值
后面我们会介绍抑制过拟合、提高泛化能力的技巧一---权值衰减（weightdecay）。简单地说，权值衰减就是一种以减小权重参数的值为目的进行学习的方法。通过减小权重参数的值来抑制过拟合的发生。如果想减小权重的值，一开始就将初始值设为较小的值才是正途。实际上，在这之前的权重初始值都是像0.01*np.random.randn（10，100）这样，使用由高斯分布生成的值乘以0.01后得到的值（标准差为0.01的高斯分布 ）。
如果我们把权重初始值全部设为0以减小权重的值，会怎么样呢？从结论来说，将权重初始值设为0不是一个好主意。事实上，将权重初始值设为0的话，将无法正确进行学习。
为什么不能将权重初始值设为0呢？严格地说，为什么不能将权重初始值设成一样的值呢？这是因为在误差反向传播法中，所有的权重值都会进行相同的更新。比如，在2层神经网络中，假设第1层和第2层的权重为0。这样一来，正向传播时，因为输人层的权重为0，所以第2层的神经元全部会被传递相同的值。第2层的神经元中全部输人相同的值，这意味着反向传播时第2层的权重全部都会进行相同的更新。为了防止权重均一化，必须随机生成初始值。
使用标准差为1的高斯分布作为权重初始值时的各层激活值的分布
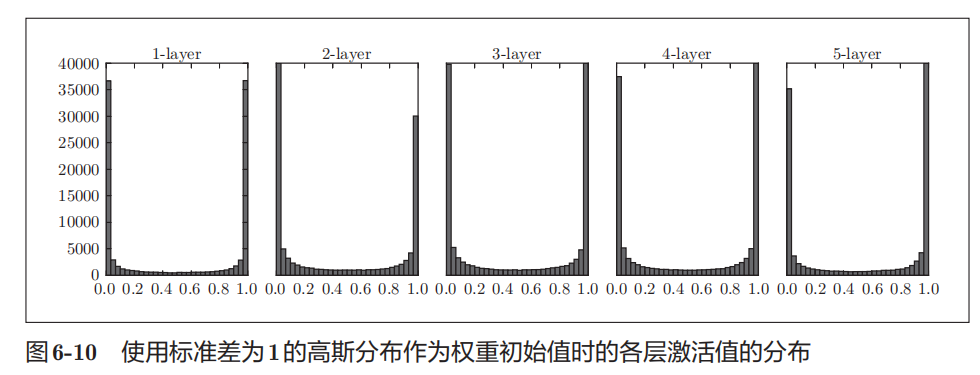
从图可知，各层的激活值呈偏向0和1的分布。这里使用的sigmoid函数是S型函数，随着输出不断地靠近0（或者靠近1），它的导数的值逐渐接近0。因此，偏向0和1的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。层次加深的深度学习中，梯度消失的问题可能会更加严重。
使用标准差为0.01的高斯分布作为权重初始值时的各层激活值的分布
各层的激活值的分布都要求有适当的广度。为什么呢？因为通过在各层间传递多样性的数据，神经网络可以进行高效的学习。反过来，如果传递的是有所偏向的数据，就会出现梯度消失或者"表现力受限"的问题，导致学习可能无法顺利进行。
接着，我们尝试使用XavierGlorot等人的论文中推荐的权重初始值（俗称**"Xavier初始值"** ）。现在，在一般的深度学习框架中，Xavier初始值已被作为标准使用。比如，Caffe框架中，通过在设定权重初始值时赋予xavier参数，就可以使用Xavier初始值。
Xavier的论文中，为了使各层的激活值呈现出具有相同广度的分布，推导了合适的权重尺度。推导出的结论是，如果前一层的节点数为n，则初始值使用标准差为的分布。
使用Xavier初始值作为权重初始值时的各层激活值的分布。
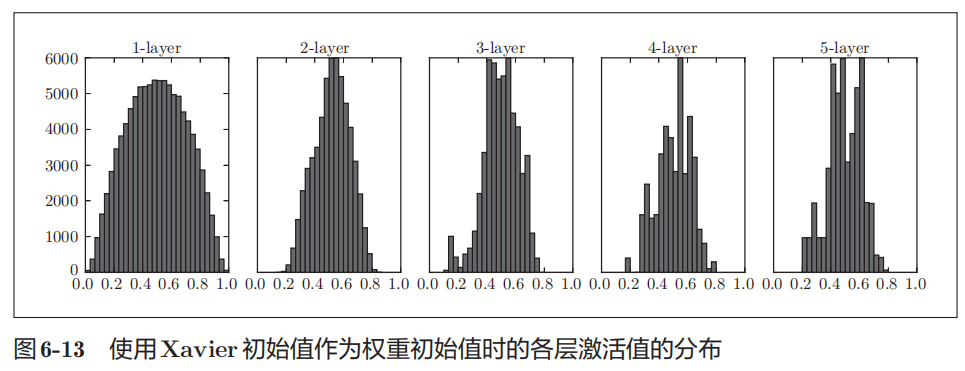
图示的分布中，后面的层的分布呈稍微歪斜的形状。如果用tanh函数（双曲线函数）代替sigmoid函数，这个稍微歪斜的问题就能得到改善。实际上，使用tanh函数后，会呈漂亮的吊钟型分布。tanh函数和sigmoid函数同是S型曲线函数，但tanh函数是关于原点（0，0）
对称的S型曲线，而sigmoid函数是关于（c，y）=（0,0.5）对称的S型曲线。众所周知，用作激活函数的函数最好具有关于原点对称的性质。
Xavier初始值是以激活函数为线性函数推导出来的，tanh函数和sigmoid函数左右对称，且在中央附近可以视作线性函数。
但当激活函数使用ReLU时，一般推荐使用ReLU专用的初始值，也就是KaimingHe等人推荐的初始值，也称为**"He初始值"** 。当前一层的节点数为n时，He初始值使用标准差为的高斯分布。当Xavier初始值是
时，（直观上）可以解释为，因为ReLU的负值区域的值为0 ，为了使它更有广度，所以需要2倍的系数。
总结一下，当激活函数使用ReLU时，权重初始值使用He初始值，当激活函数为sigmoid或tanh等S型曲线函数时，初始值使用Xavier初始值。这是目前的最佳实践。
BatchNormalization
BatchNormalization（下文简称BatchNorm）是2015年提出的方法。BatchNorm虽然是一个问世不久的新方法，但已经被很多研究人员和技术人员广泛使用。实际上，看一下机器学习竞赛的结果，就会发现很多通过使用这个方法而获得优异结果的例子。
为什么BatchNorm这么惹人注目呢？因为BatchNorm有以下优点。
- 可以使学习快速进行（可以增大学习率）。
- 不那么依赖初始值（对于初始值不用那么神经质）。
- 抑制过拟合（降低Dropout等的必要性）。
如前所述，BatchNorm的思路是调整各层的激活值分布使其拥有适当的广度。为此，要向神经网络中插人对数据分布进行正规化的层，即BatchNormalization层（下文简称BatchNorm层），如图所示。
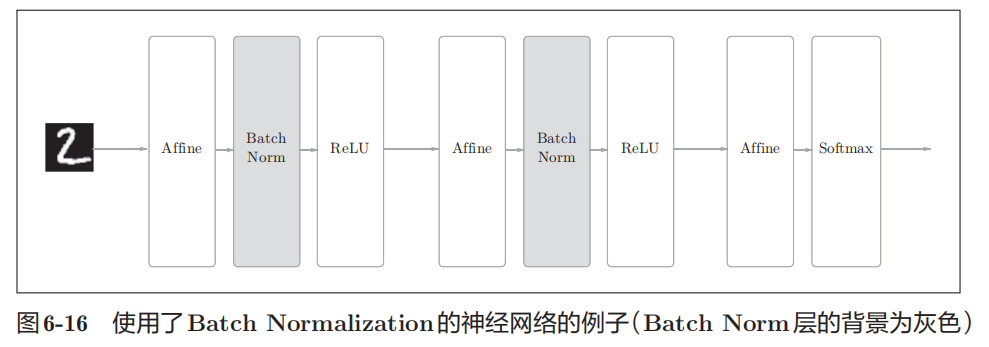
BatchNorm，顾名思义，以进行学习时的mini-batch为单位，按mini-batch进行正规化 。具体而言，就是进行使数据分布的均值为0、方差为1的正规化。用数学式表示的话，如下所示。
式中是一个微小值，是为了防止出现除以0的情况发生
正则化
机器学习的问题中，过拟合是一个很常见的问题。过拟合指的是只能拟合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。机器学习的目标是提高泛化能力，即便是没有包含在训练数据里的未观测数据，也希望模型可以进行正确的识别。我们可以制作复杂的、表现力强的模型。发生过拟合的原因，主要有以下两个：
- 模型拥有大量参数、表现力强。
- 训练数据少。
权值衰减 是一直以来经常被使用的一种抑制过拟合的方法。该方法通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。很多过拟合原本就是因为权重参数取值过大 才发生的。
复习一下，神经网络的学习目的是减小损失函数的值。这时，例如为损失函数加上权重的平方范数（L2范数）。这样一来，就可以抑制权重变大。用符号表示的话，如果将权重记为W，L2范数的权值衰减就是，然后将这个
加到损失函数上。这里，
是控制正则化强度的超参数。
设置得越大，对大的权重施加的惩罚就越重。此外，
开头的
是用于将
的求导结果变成
的调整用常量。
对于所有权重，权值衰减方法都会为损失函数加上。因此，在求权重梯度的计算中，要为之前的误差反向传播法的结果加上正则化项的导数
。
Dropout
作为抑制过拟合的方法，如果网络的模型变得很复杂，只用权值衰减就难以应对了。在这种情
况下，我们经常会使用Dropout方法。
Dropout是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除。被删除的神经元不再进行信号的传递。训练时，每传递一次数据，就会随机选择要删除的神经元。然后，测试时，虽然会传递所有的神经元信号，但是对于各个神经元的输出，要乘上训练时的删除比例后再输出。
|--------------------------------------------------------------------------------|--------------------------------------------------------------------------------|
| 删除前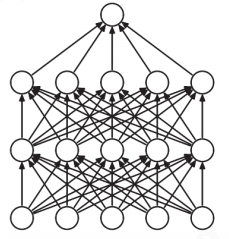 
| 删除后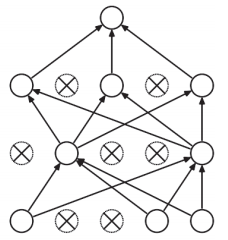 
|
机器学习中经常使用集成学习 。所谓集成学习，就是让多个模型单独进行学习，推理时再取多个模型的输出的平均值。用神经网络的语境来说，比如，准备5个结构相同（或者类似）的网络，分别进行学习，测试时，以这5个网络的输出的平均值作为答案。实验告诉我们，
通过进行集成学习，神经网络的识别精度可以提高好几个百分点。这个集成学习与Dropout有密切的关系。这是因为可以将Dropout理解为，通过在学习过程中随机删除神经元，从而每一次都让不同的模型进行学习。并且，推理时，通过对神经元的输出乘以删除比例（比如，0.5等），可以取得模型的平均值。也就是说，可以理解成，Dropout将集成学习的效果（模拟地）通过一个网络实现了。
超参数的验证
神经网络中，除了权重和偏置等参数，超参数（hyper-parameter） 也经常出现。这里所说的超参数是指，比如各层的神经元数量、batch大小、参数更新时的学习率或权值衰减等。如果这些超参数没有设置合适的值，模型的性能就会很差。虽然超参数的取值非常重要，但是在决定超参数的过程中一般会伴随很多的试错。本节将介绍尽可能高效地寻找超参数的值的方法。
注意：不能使用测试数据评估超参数的值
调整超参数的数据，一般称为验证数据（validation data），我们可以用这个验证数据来评价超参数的好坏。
超参数的范围只要"大致地指定"就可以了。所谓"大致地指定"，是指像0.001到1000这样，以"10的阶乘"的尺度指定范围（也表述为"用对数尺度（log scale） 指定"）。
在超参数的最优化中，要注意的是深度学习需要很长时间（比如，几天或几周）。因此，在超参数的搜索中，需要尽早放弃那些不符合逻辑的超参数。于是，在超参数的最优化中，减少学习的epoch，缩短一次评估所需的时间是一个不错的办法。
以上就是超参数的最优化的内容，简单归纳一下，如下所示。
- 步骤0：设定超参数的范围。
- 步骤1：从设定的超参数范围中随机采样。
- 步骤2：使用步骤1中采样到的超参数的值进行学习，通过验证数据评估识别精度（但是要将epoch设置得很小）。
- 步骤3：重复步骤1和步骤2（100次等），根据它们的识别精度的结果，缩小超参数的范围。
在超参数的最优化中，如果需要更精炼的方法，可以使用贝叶斯最优（Bayesianoptimization）。贝叶斯最优化运用以贝叶斯定理为中心的数学理论，能够更加严密、高效地进行最优化。详细内容请参考论文"Practical BayesianOptimizationofMachineLearningAlgorithms"等。
第七章：卷积神经网络
本章的主题是卷积神经网络（ConvolutionalNeuralNetwork，CNN）。CNN被用于图像识别、语音识别等各种场合，在图像识别的比赛中，基于深度学习的方法几乎都以CNN为基础。本章将详细介绍CNN的结构，并用Python实现其处理内容。
整体结构
CNN可以通过组装层来构建。不过，CNN中新出现了卷积层（Convolution层）和池化层（Pooling层） 。相邻层的所有神经元之间都有连接，这称为全连接（fully-connected）。另外，我们用Affine层实现了全连接层。如图所示，这里堆叠了4层"Affine-ReLU"组合，然后第5层是Afine层，最后由Softmax层输出最终结果（概率）。
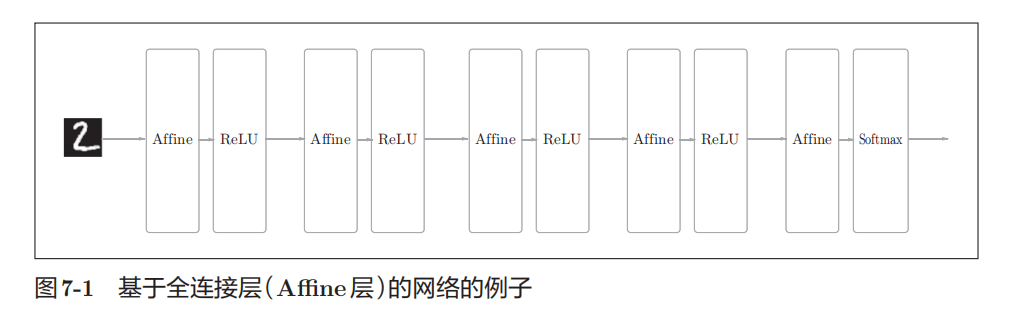
增加了卷积层
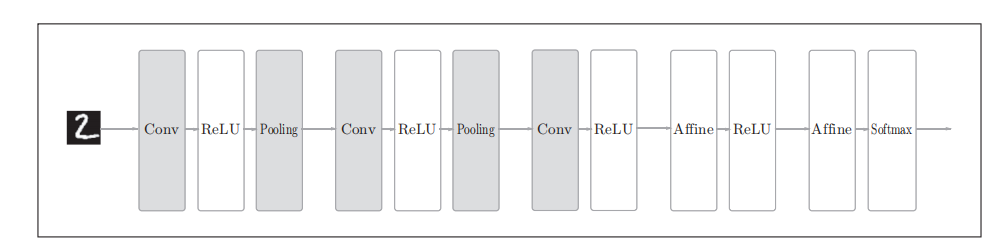
全连接层的问题是，数据的形状被忽略了，将全部的输人数据作为相同的神经元（同一维度的神经元）处理，所以无法利用与形状相关的信息。而卷积层可以保持形状不变。当输人数据是图像时，卷积层会以3维数据的形式接收输人数据，并同样以3维数据的形式输出至下一层。因此，在CNN中，可以（有可能）正确理解图像等具有形状的数据。
另外，CNN中，有时将卷积层的输人输出数据称为特征图（featuremap） 。其中，卷积层的输人数据称为输入特征图 （inputfeaturemap），输出数据称为输出特征图（outputfeaturemap）。本书中将"输人输出数据"和"特征图"作为含义相同的词使用。
卷积运算相当于图像处理中的滤波器运算。
**填充（padding）：**在进行卷积层的处理之前，有时要向输人数据的周围填人固定的数据
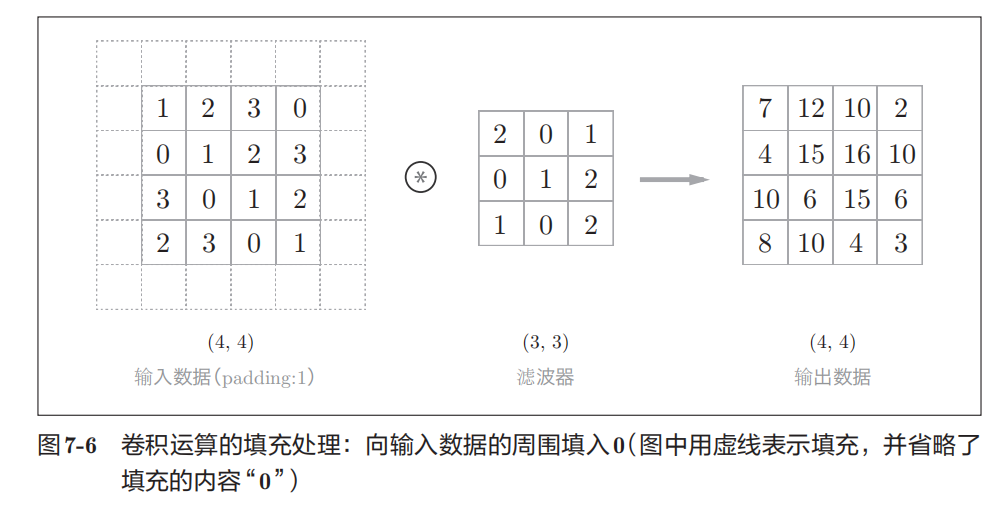
应用滤波器的位置间隔称为步幅（stride）：
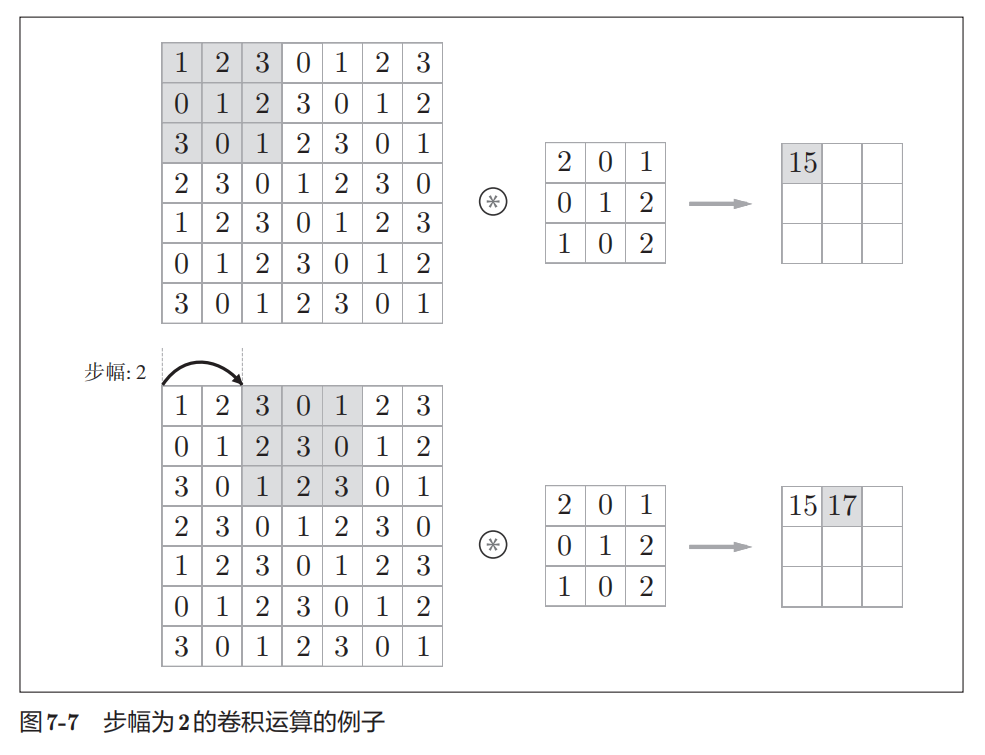
增大步幅S后输出大小会变小，增大填充P后，输出大小会变大，假设输入大小为（H,W），滤波器大小为(FH,FW)，输出大小为
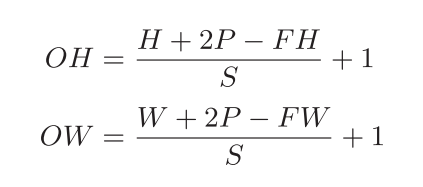
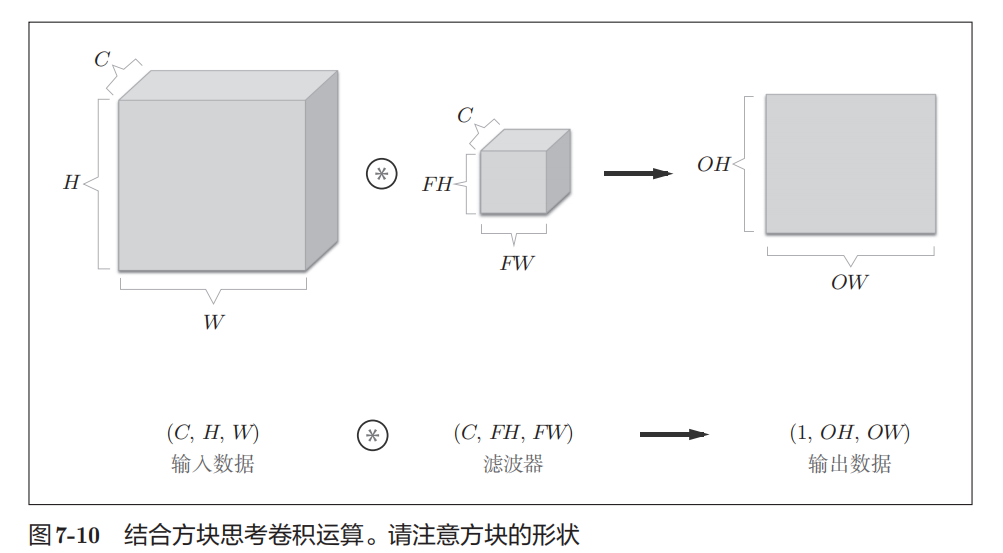
这张数据输出是一张特征图，也就是通道数为1 的特征图，如果要在通道方向拥有多个卷积运算的输出，就需要用到多个滤波器（权重）
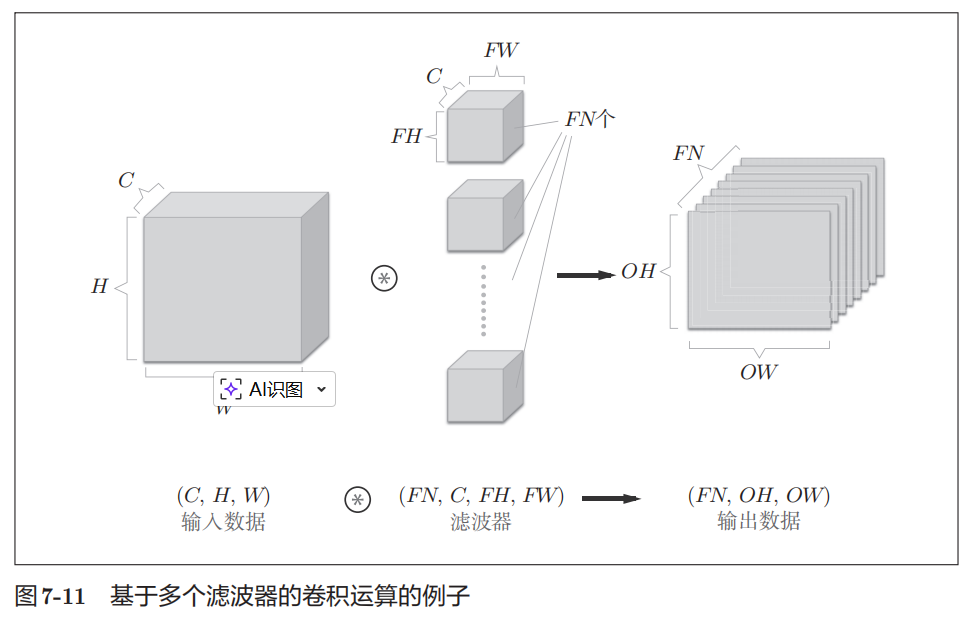
如图7-11所示，关于卷积运算的滤波器，也必须考虑滤波器的数量。因此，作为4维数据，滤波器的权重数据要按**(output_channel,inputchannel, height, width)**的顺序书写。比如，通道数为3、大小为5x5的滤波器有 20个时，可以写成(20,3,5,5)。
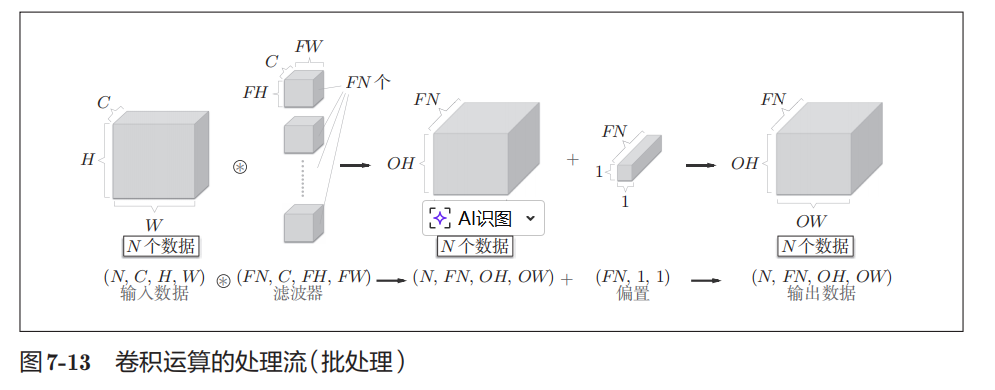
通过批处理，能够实现处理的高效化和学习时对mini-batch的对应
池化层
池化是缩小高长方向的运算
Max池化是获取最大值的运算
除了Max池化外，还有Average池化等。Max池化是从目标区域中获取最大值，Average池化则是计算目标区域的平均值。在图像识别领域，主要使用Max池化。
池化层的特征
- 没有要学习的参数：池化只从目标区域取值，并没有学习
- 通道数不发生变化：计算是按通道独立的
- 对微小的位置变化具有鲁棒性（健壮）：数据发生微小偏差池化仍然返回相同结果
卷积层和池化层的实现
CNN中各层间传递的是四维数据，比如数据的形状为（10,1,28,28），则它对应10个高为28宽为28通道为1的数据，用python实现
im2col
如果计算卷积，则要用到for循环，会拖慢速度，所以不采用for函数，采用im2col将数据展开。
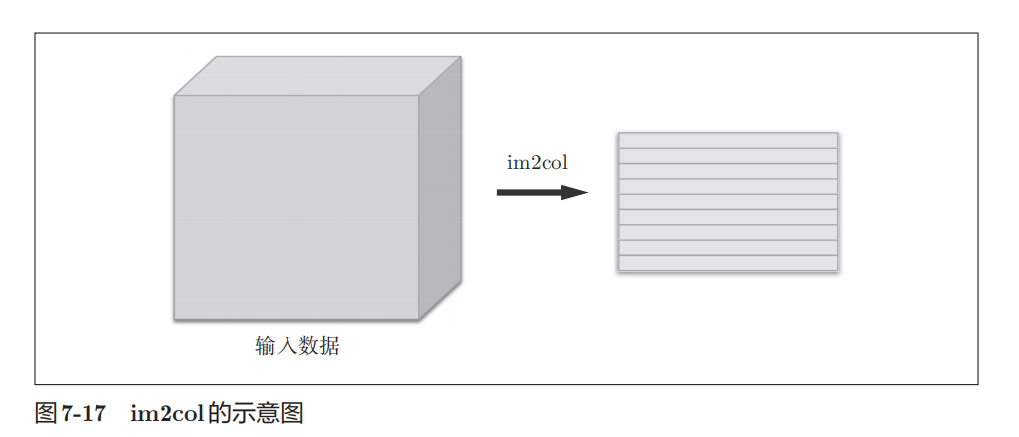
im2col将数据展开以适应滤波器（权重），image to column，从图像到矩阵的意思。
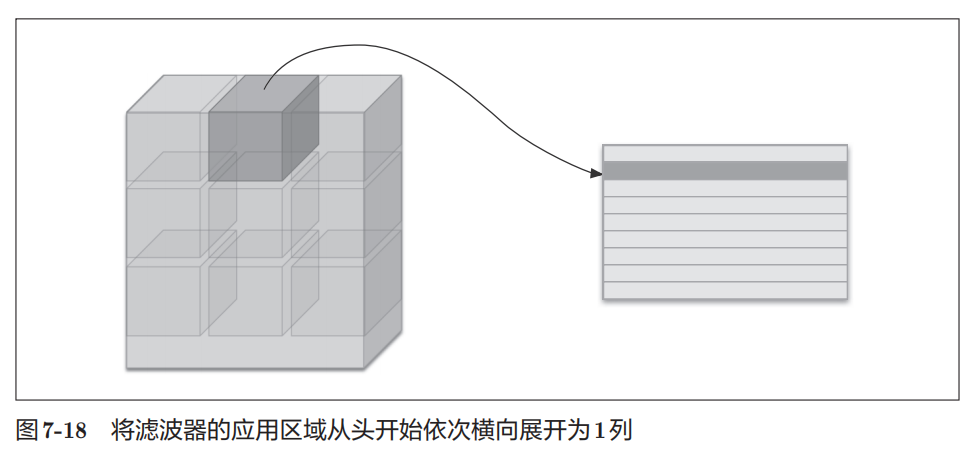
池化层也一样需要展开
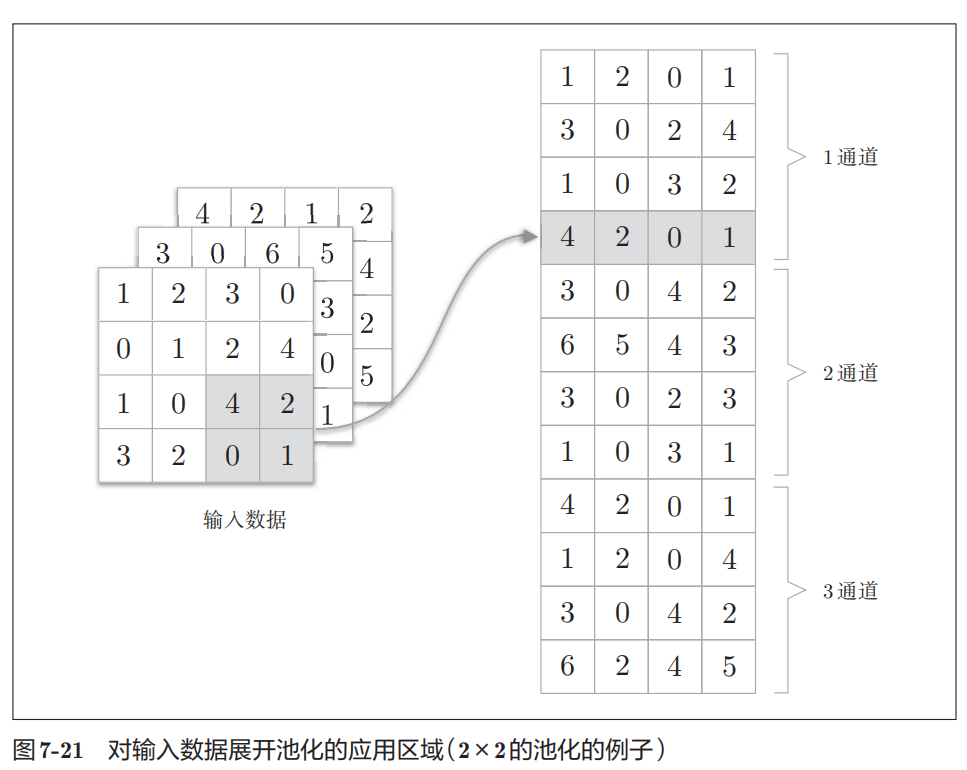
CNN的实现
已经实现了卷积层和池化层，现在组合这些层就能搭建网络了
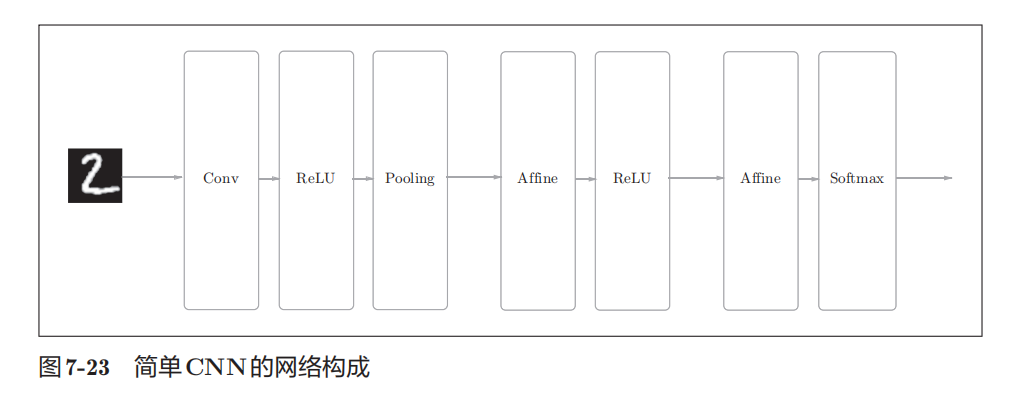
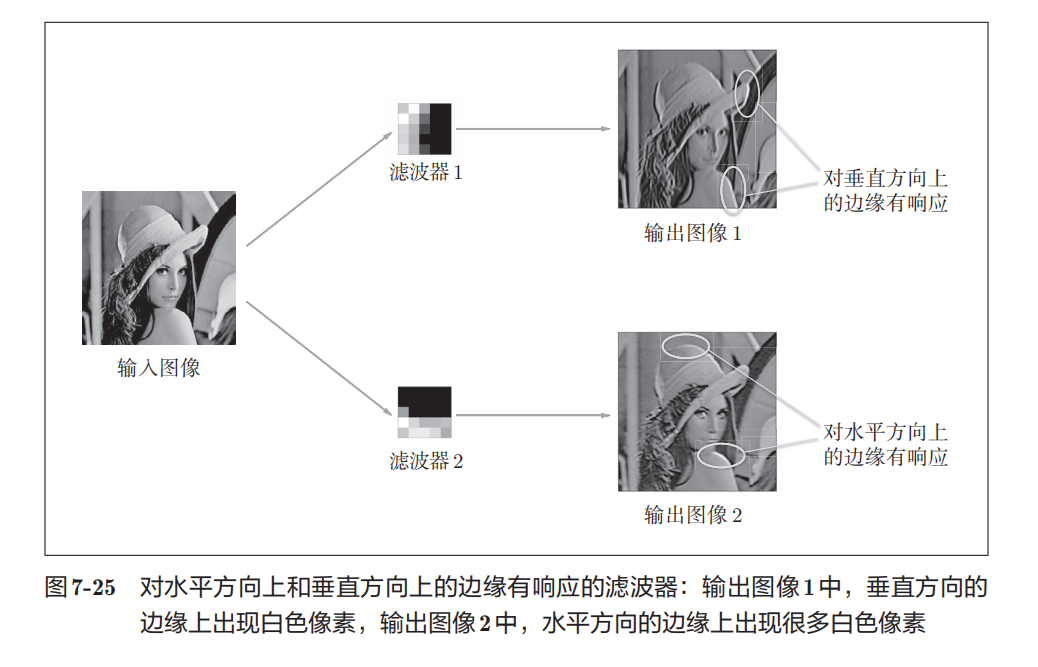
CNN的可视化：通过卷基层的可视化，探索CNN进行了什么处理
右边有规律的滤波器在观察边缘（颜色变化的分界线）和斑块（局部的块状区域）
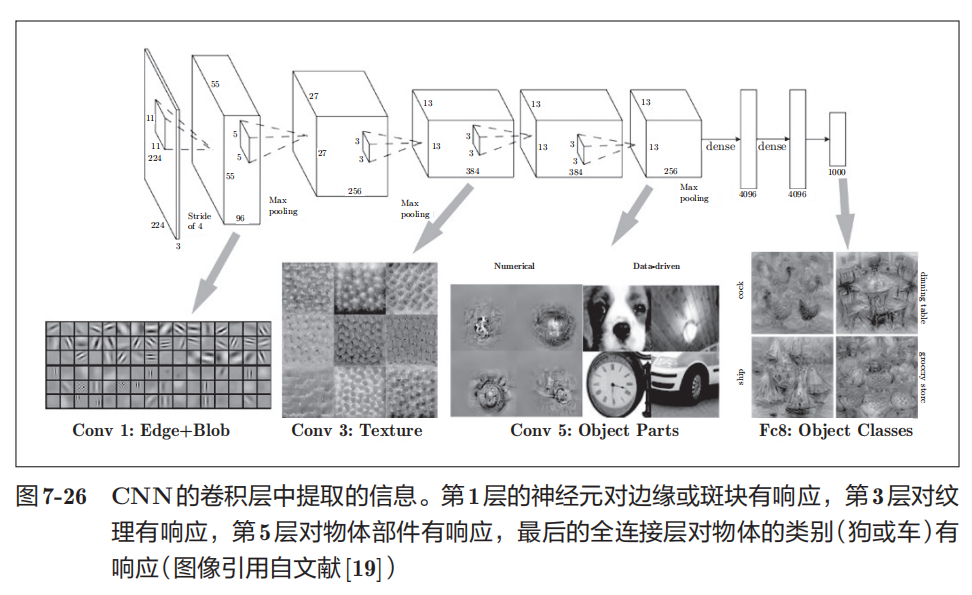
具有代表性的CNN
|-------------|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| LeNet | LeNet 在 1998 年被提出，是进行手写数字识别的网络。如图 所示， 它有连续的卷积层和池化层（正确地讲，是只"抽选元素"的子采样层），最 后经全连接层输出结果。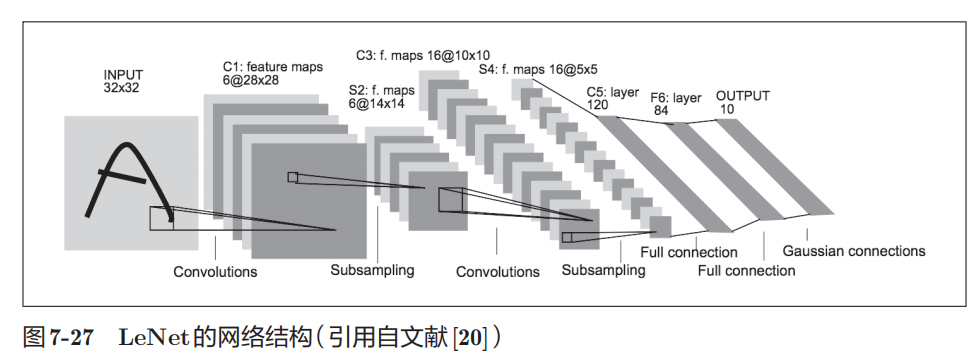 
LeNet激活函数采用sigmoid函数，现在CNN采用ReLU函数 |
| AlexNet |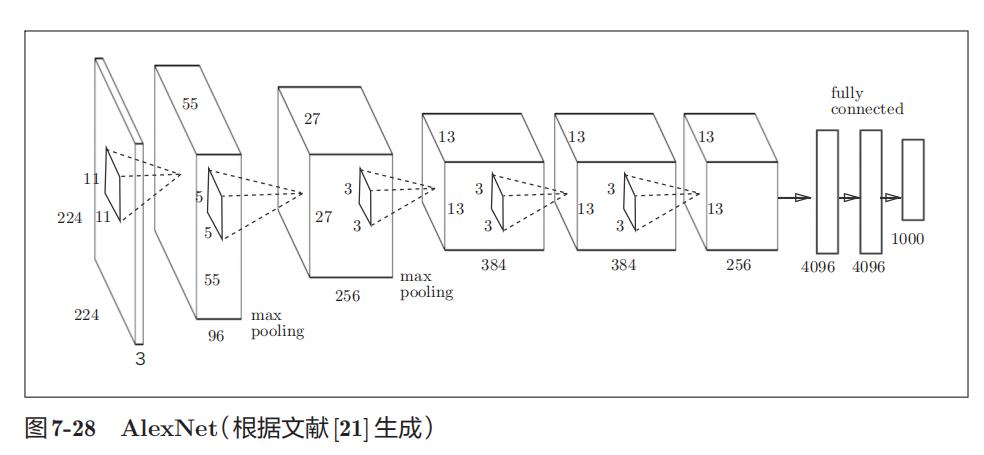 
上 AlexNet 和 LeNet差异 * 激活函数使用ReLU。 * 使用进行局部正规化的LRN（Local Response Normalization）层。 * 使用Dropout |
第八章：深度学习
还是以手写数字识别的网络结构为例
在一个标题为" What is the class of this image ? "的网站 [32] 上，以排行榜的形式刊登了目前为止通过论文等渠道发表的针对各种数据集的方法的识别精度（图8-3 ）。
参考刚才排行榜中前几名的方法，可以发现进一步提高识别精度的技术和 线索。比如，集成学习、学习率衰减、Data Augmentation（数据扩充）等都有 助于提高识别精度。尤其是Data Augmentation，虽然方法很简单，但在提高 识别精度上效果显著。
Data Augmentation基于算法"人为地"扩充输入图像（训练图像）。具体地说，如图8-4 所示，对于输入图像，通过施加旋转、垂直或水平方向上的移动等微小变化，增加图像的数量。这在数据集的图像数量有限时尤其有效。
加深层的好处
可以减少网络的参数数量
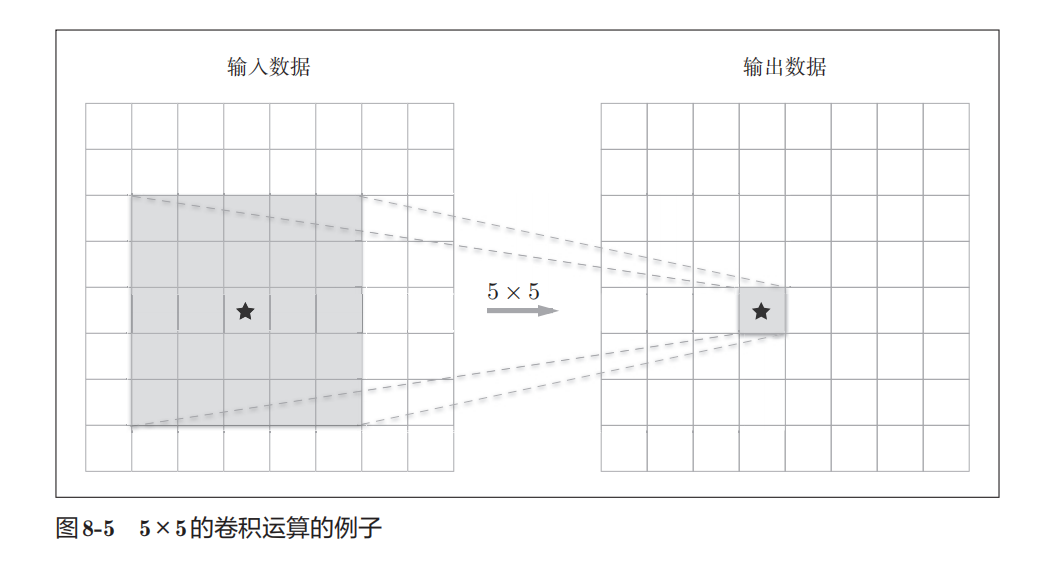
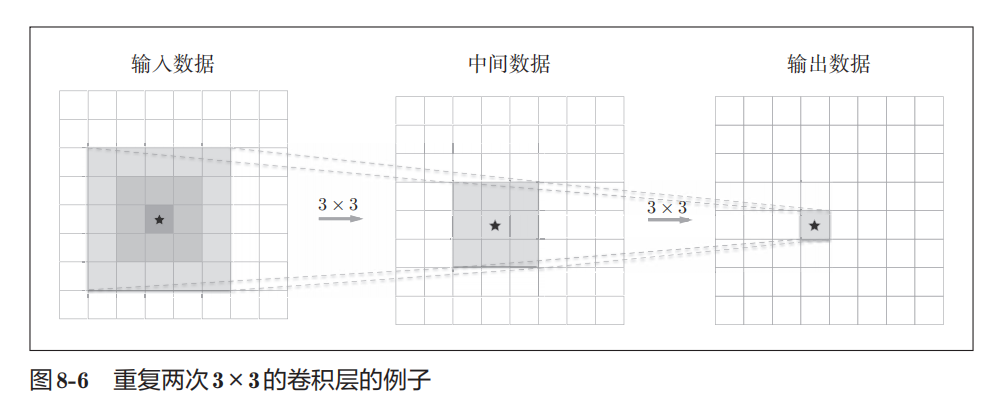
对比以上两种处理， 一次 5 × 5 的卷积运算的区域可以由两次 3 × 3 的卷积运算抵充。并且， 相对于前者的参数数量 25 （ 5 × 5 ），后者一共是 18 （ 2 × 3 × 3 ），通过叠加卷 积层，参数数量减少了。而且，这个参数数量之差会随着层的加深而变大。
叠加小型滤波器来加深网络的好处是可以减少参数的数量，扩大 感受野（receptive field，给神经元施加变化的某个局部空间区域）。并且，通过叠加层，将 ReLU等激活函数夹在卷积层的中间，进一步提高了网络的表现力。这是因为向网络添加了基于激活函数的"非线性"
表现力，通过非线性函数的叠加，可以表现更加复杂的东西。
ILSVRC 大赛有多个测试项目，其中之一是"类别分类"（ classification ），在该项目中，会进行1000 个类别的分类，比试识别精度。我们来看一下最近几年的ILSVRC 大赛的类别分类项目的结果。图 8-8 中展示了从 2010 年到2015年的优胜队伍的成绩。这里，将前 5 类中出现正确解的情况视为"正确"，此时的错误识别率用柱形图来表示。
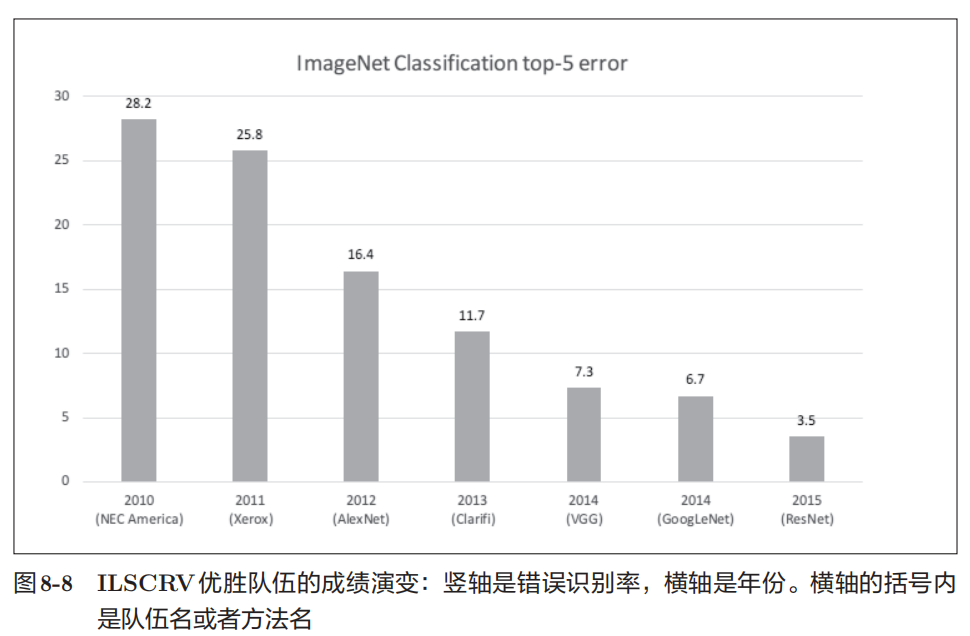
介绍这些网络结构
|---------------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| VGG | VGG 是由卷积层和池化层构成的基础的 CNN 。不过，如图 8-9 所示， 它的特点在于将有权重的层（卷积层或者全连接层）叠加至16 层（或者 19 层），具备了深度（根据层的深度，有时也称为"VGG16 "或" VGG19 "）。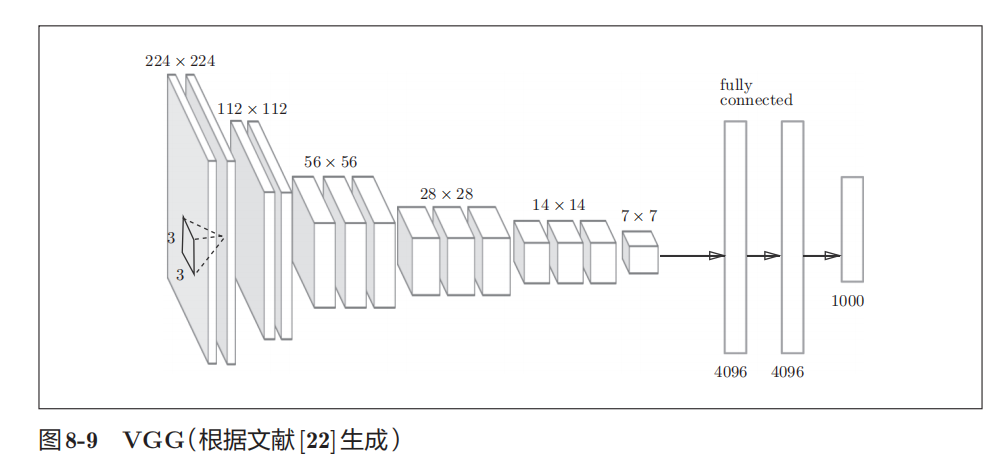 
|
| GoogLeNet |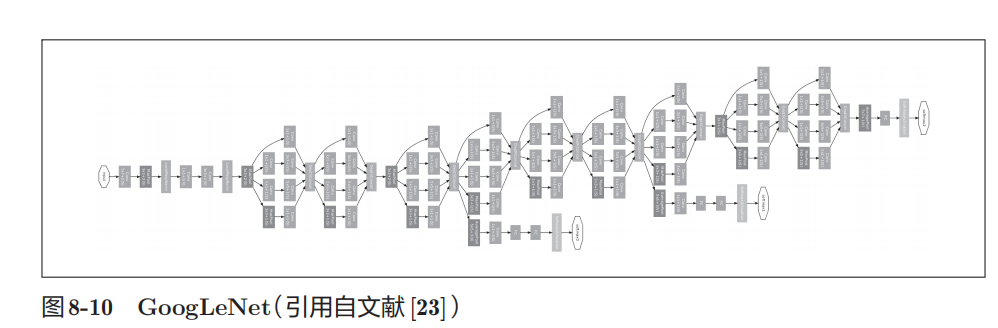 
|
| ResNet |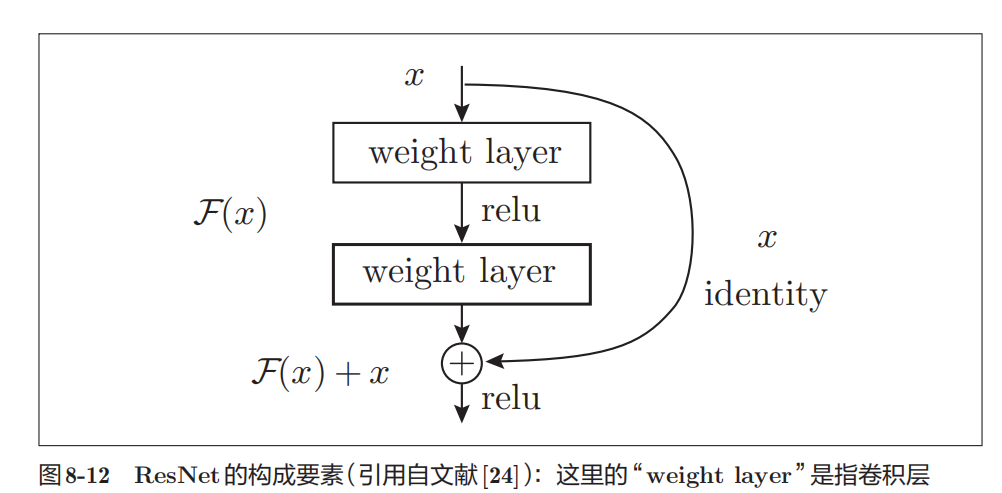 
我们已经知道加深层对于提升性能很重要。但是，在深度学习中，过度 加深层的话，很多情况下学习将不能顺利进行，导致最终性能不佳。ResNet 中， 为了解决这类问题，导入了"快捷结构"（也称为"捷径"或"小路"）。导入这 个快捷结构后，就可以随着层的加深而不断提高性能了（当然，层的加深也 是有限度的）。 
|
深度学习的高速化
GPU原本是作为图像专用的显卡使用的，但最近不仅用于图像处理， 也用于通用的数值计算。由于GPU 可以高速地进行并行数值计算，因此 GPU 计算 的目标就是将这种压倒性的计算能力用于各种用途。所谓 GPU 计算，是指基于GPU 进行通用的数值计算的操作。
GPU主要由 NVIDIA 和 AMD 两家公司提供。虽然两家的 GPU 都可以 用于通用的数值计算，但与深度学习比较"亲近"的是NVIDIA 的 GPU 。实际上，大多数深度学习框架只受益于NVIDIA 的 GPU 。这是因为深度学习的框架中使用了NVIDIA 提供的 CUDA 这个面向 GPU 计算的综合开发环境。
应用案例
物体检测
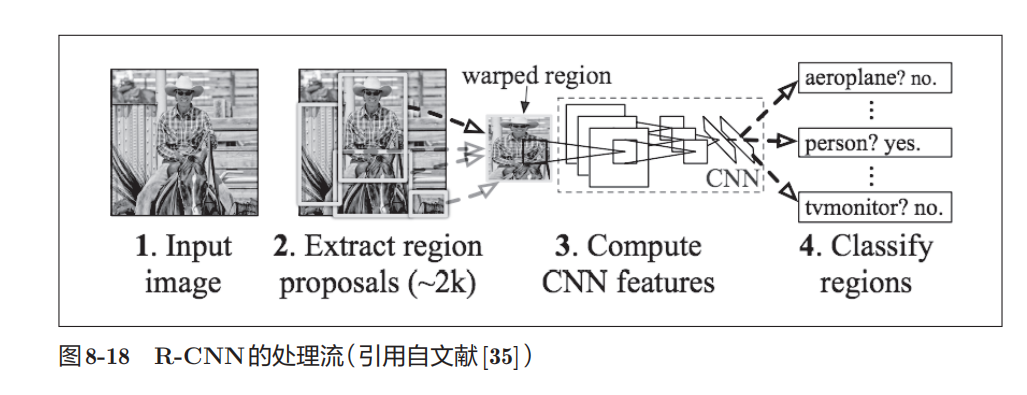
图像分割
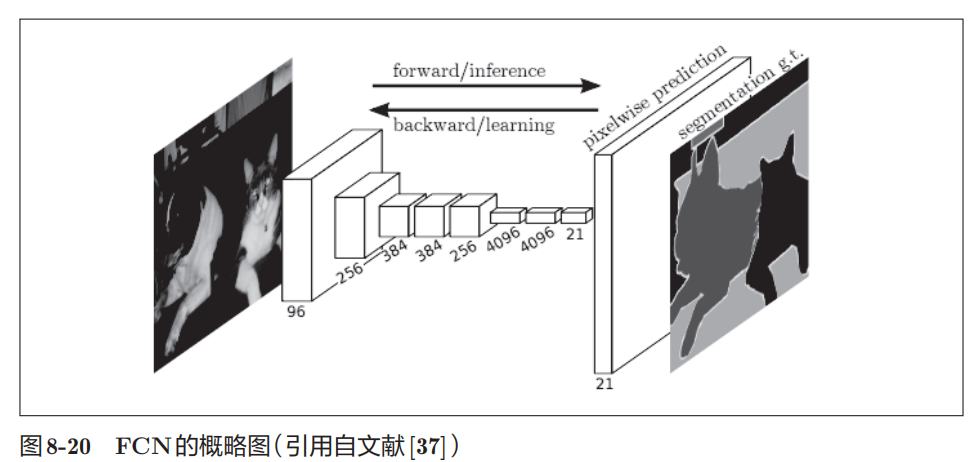
有人提出了一个名为 FCN （ Fully Convolutional Network） [37] 的方法。该方法通过一次 forward 处理，对所有像素进行分类。 FCN的字面意思是"全部由卷积层构成的网络"。相对于一般的 CNN 包 含全连接层，FCN 将全连接层替换成发挥相同作用的卷积层。
FCN 的特征在于最后导入了扩大空间大小的处理。基于这个处理，变小了的中间数据可以一下子扩大到和输入图像一样的大小。FCN最后进行的扩大处理是基于双线性插值法的扩大（双线性插值扩大）。FCN中，这个双线性插值扩大是通过去卷积（逆卷积运算）来实现的（细节请参考FCN 的论文 [37] ）
图像标题的生成
一个基于深度学习生成图像标题的代表性方法是被称为 NIC（ Neural Image Caption）的模型。如图 8-22 所示， NIC 由深层的 CNN 和处理自然语言的RNN （ Recurrent Neural Network ）构成。 RNN 是呈递归式连接的网络，经常被用于自然语言、时间序列数据等连续性的数据上。
NIC 是组合了两个神经网络（ CNN 和 RNN ）的简单结构。基于NIC ，可以生成惊人的高精度的图像标题。我们将组合图像和自然语言等多种信息进行的处理称为多模态处理 。
图像风格变换
图像的生成
基 于 DCGAN （ Deep Convolutional Generative Adversarial Network ） 方法生成的卧室图像的例子。
之前我们见到的机器学习问题都是被称为 监督学习 （supervised learning）的问题。这类问题就像手写数字识别一样，使用的是图像数据和教师标签成对给出的数据集。不过这里讨论的问题，并没有给出监督数据，只给了大量的图像（图像的集合），这样的问题称为无监督学习（unsupervised learning）。无监督学习虽然是很早之前就开始研究的领域（Deep Belief Network、Deep Boltzmann Machine等很有名），但最近似乎并不是很活跃。今后，随着使用深度学习的DCGAN等方法受到关注，无监督学习有望得到进一步发展。
自动驾驶
比如，基于 CNN 的神经网络 SegNet [42] ，可以像图 8-25 那样高精度地识别行驶环境。
Deep Q-Network（强化学习）
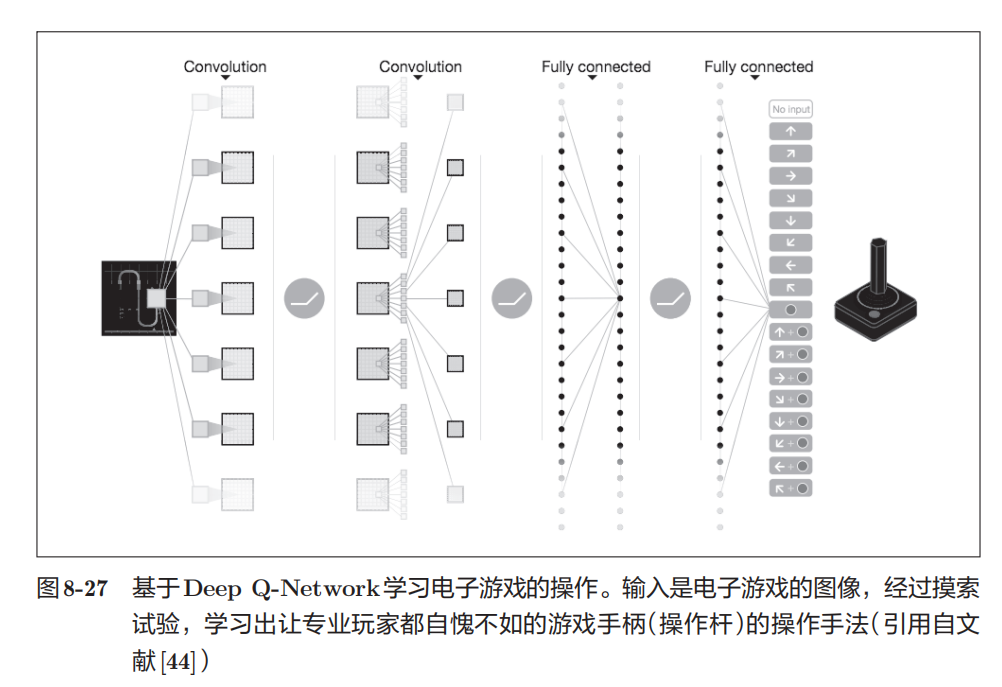
就像人类通过摸索试验来学习一样（比如骑自行车），让计算机也在摸索试验的过程中自主学习，这称为强化学习 （ reinforcement learning ）。强化学习和有"教师"在身边教的"监督学习"有所不同。强化学习的基本框架是，代理（Agent ）根据环境选择行动，然后通过这个行动改变环境。根据环境的变化，代理获得某种报酬。强化学习的目的是决定代理的行动方针，以获得更好的报酬（图8-26 ）。
在使用了深度学习的强化学习方法中，有一个叫作 Deep Q-Network （通称DQN ） [44] 的方法。该方法基于被称为 Q 学习的强化学习算法。
