引言
- 模型规模是提升模型性能的关键因素之一。在有限的计算资源预算下,用更少的训练步数训练一个更大的模型,往往比用更多的步数训练一个较小的模型效果更佳。
MOE 整体介绍
-
混合专家模型 (MoE:Mixed Expert Models) :一种稀疏激活的深度学习架构范式,核心思想是:将复杂任务拆解为多个子任务,由专业化的 "专家子网络" 并行处理,再通过 "门控网络" 动态选择并融合 Top-K 专家的输出
- 显著优势是它们能够在远少于稠密模型所需的计算资源下进行有效的预训练。这意味着在相同的计算预算条件下,您可以显著扩大模型或数据集的规模。特别是在预训练阶段,与稠密模型相比,混合专家模型通常能够更快地达到相同的质量水平。
-
相比较于传统稠密模型基础 MOE 的特点:
- 与稠密模型相比, MoE预训练速度更快。
- 与具有相同参数数量的模型相比,具有更快的推理速度。
- 需要大量显存,因为所有专家系统都需要加载到内存中。
-
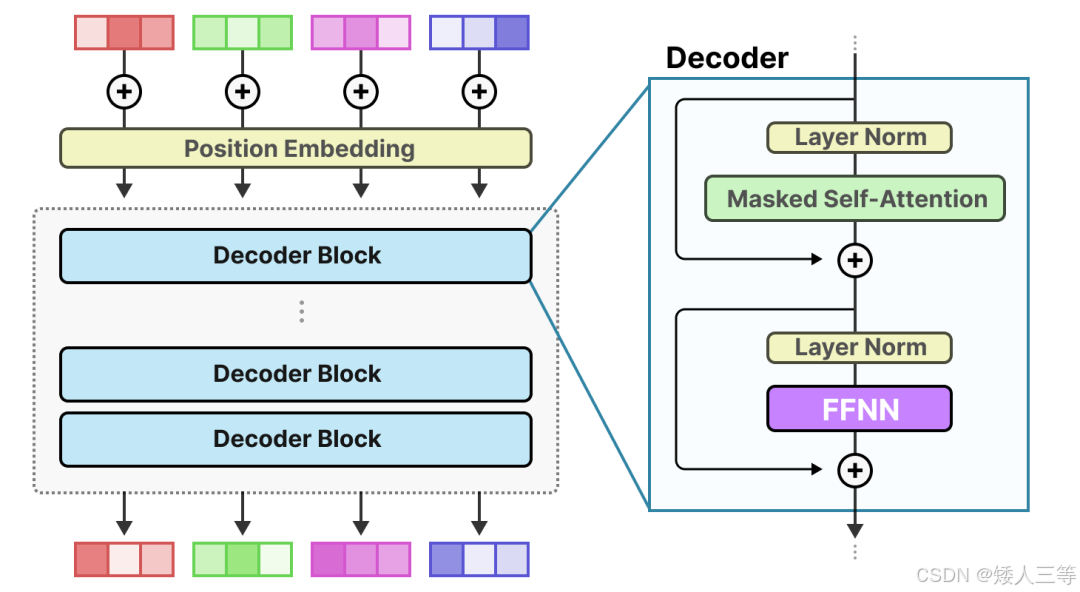
作为一种基于 Transformer 架构的模型,混合专家模型主要由两个关键部分组成:
-
稀疏 MoE 层(专家模块 Experts): 这些层通常代替了传统 Transform 模型中的前馈网络 (FFN) 层(而非 FFN 子模块,子模块是包含 Add&Norm 部分的),形成 MoE-Transformer。
-
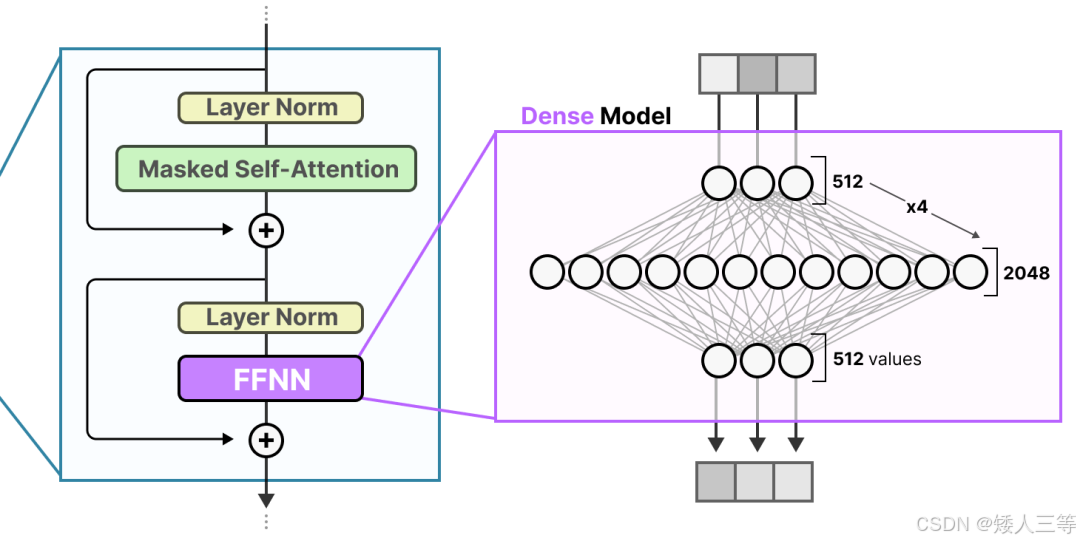
为什么替换FFN 层呢?下图为 FFN 层对于向量信息的维度处理的可视化
-
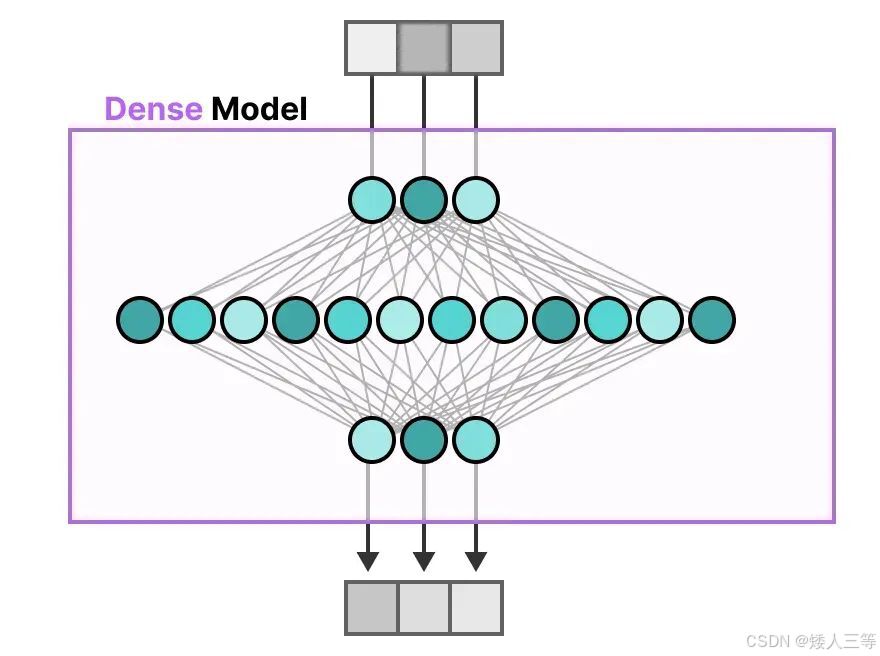
稠密 FFN 的痛点:原本 transform 中的 FFN 需要处理所有类型的 token(如下图 2所示:一段话中不同类型的 token),但所有的输入类型都用同一套参数,参数所包含的信息是有限的,输入类型是多样的;且推理时所有参数都要参与计算 (如下图 1),大模型下计算成本极高。

-
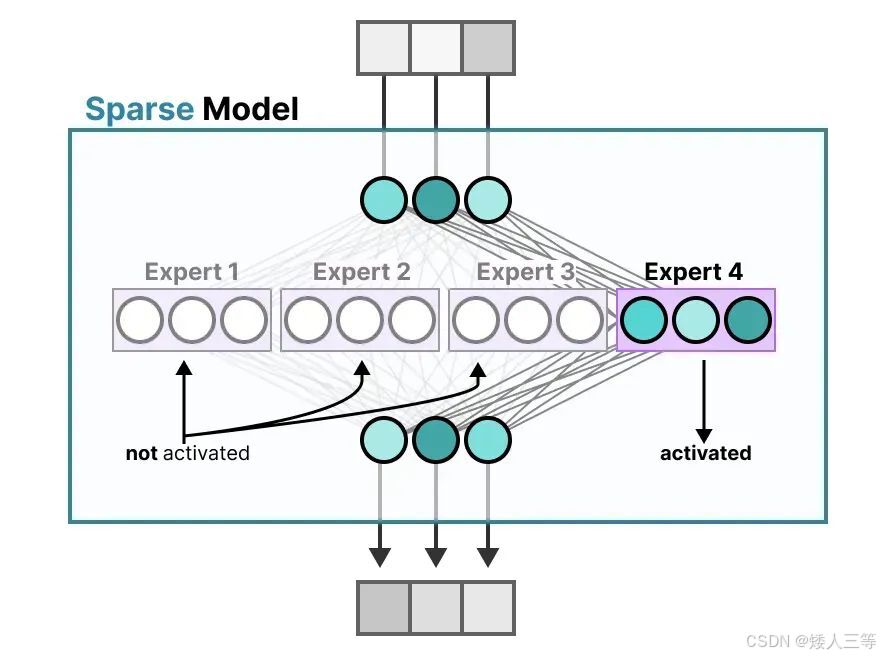
MOE 的优势:用"多专家 FFN + 门控" 替换单 FFN,实现稀疏激活 ,即每个 token 只激活 1~2 个专家,拥有多个专家(每个专家都有一套完成 FFN),虽然总参数量大幅提升,但推理计算量只和 K(激活专家数)成正比 ,在不增太多算力的前提下,扩大模型能处理的输入任务类型。
-
-
专家网络的本质,通俗理解就是把原始的 1 个 FFN(两层),拆成 N 个结构相同、参数独立的 FFN,每个 FFN 就是一个「专家」(也可以把 FFN 替换成其他可进行专业化分工的子网络),公式:FFN(x)=W2⋅σ(W1⋅x+b1)+b2
- 对应专家公式:ei(x)=W2(i)⋅σ(W1(i)⋅x+b1(i))+b2(i) i 是表示第 i 个专家,w 和 b 表示权重和偏置,w1 和 2表示第几层
-
-
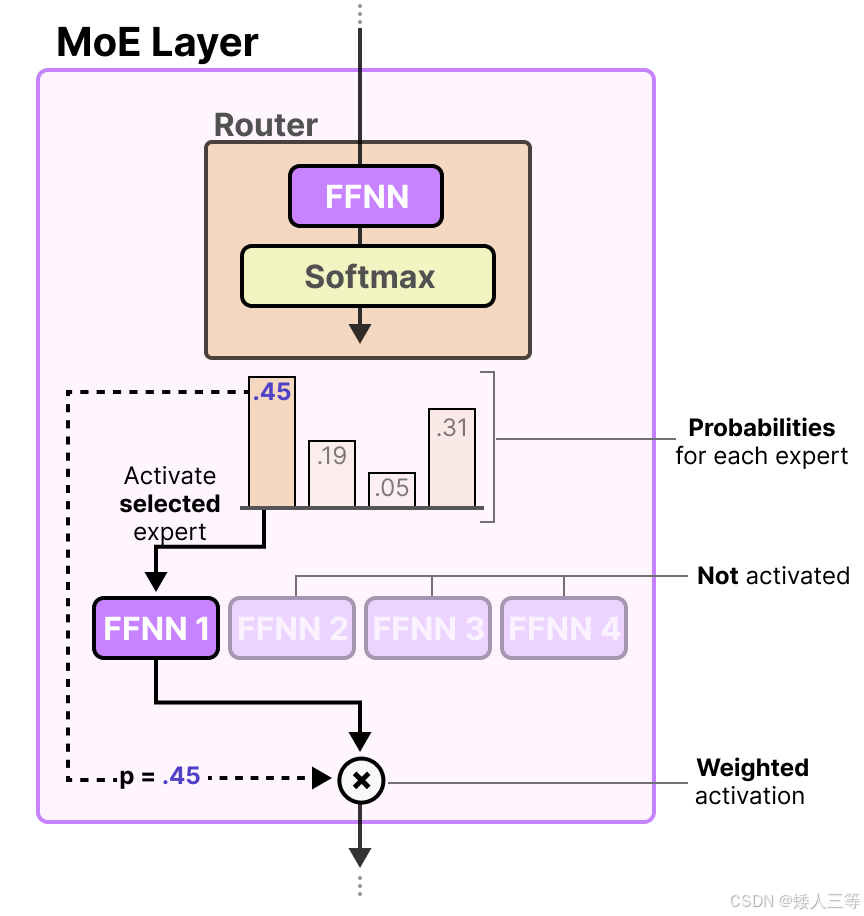
门控网络或路由: 这个部分用于决定哪些token 被发送到哪个专家,其本质也是一种前馈神经网络(FFNN),它根据特定的输入来选择专家。它输出概率,并利用这些概率来选择最匹配的专家:
- 例如,在下图 1中,"More"这个 token可能被发送到第二个专家,而"Parameters"这个token被发送到第一个专家。有时,一个token甚至可以被发送到多个专家。token的路由方式是 MoE 使用中的一个关键点,因为路由器由学习的参数组成,并且与网络的其他部分一同进行预训练。
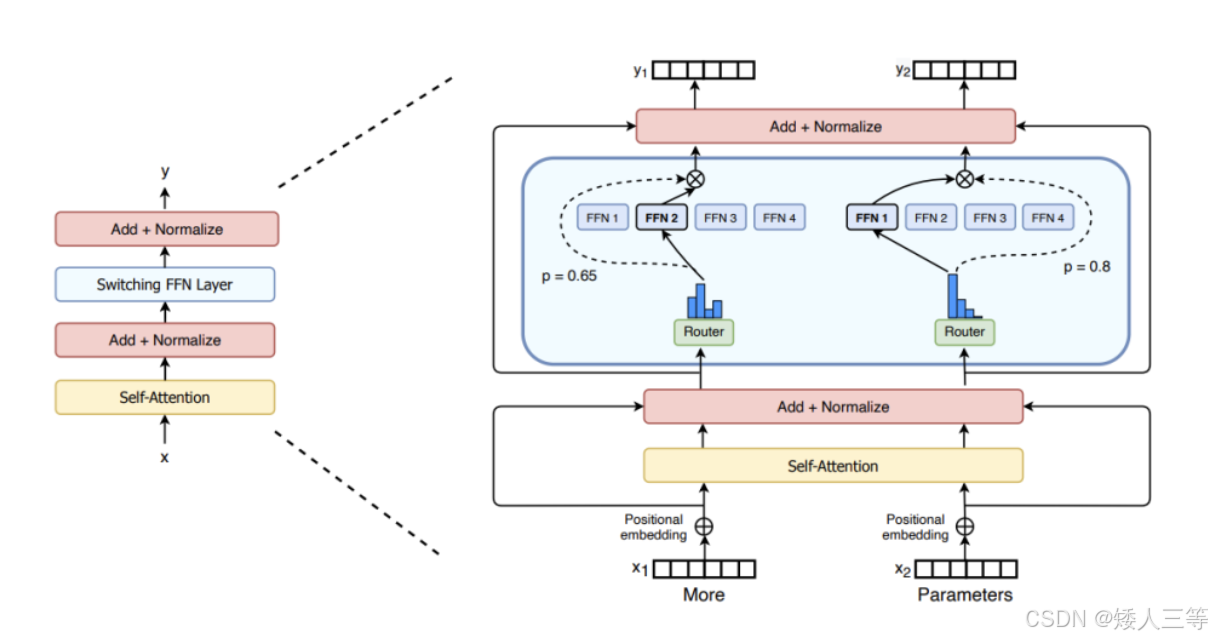
- 例如,在下图 1中,"More"这个 token可能被发送到第二个专家,而"Parameters"这个token被发送到第一个专家。有时,一个token甚至可以被发送到多个专家。token的路由方式是 MoE 使用中的一个关键点,因为路由器由学习的参数组成,并且与网络的其他部分一同进行预训练。
-
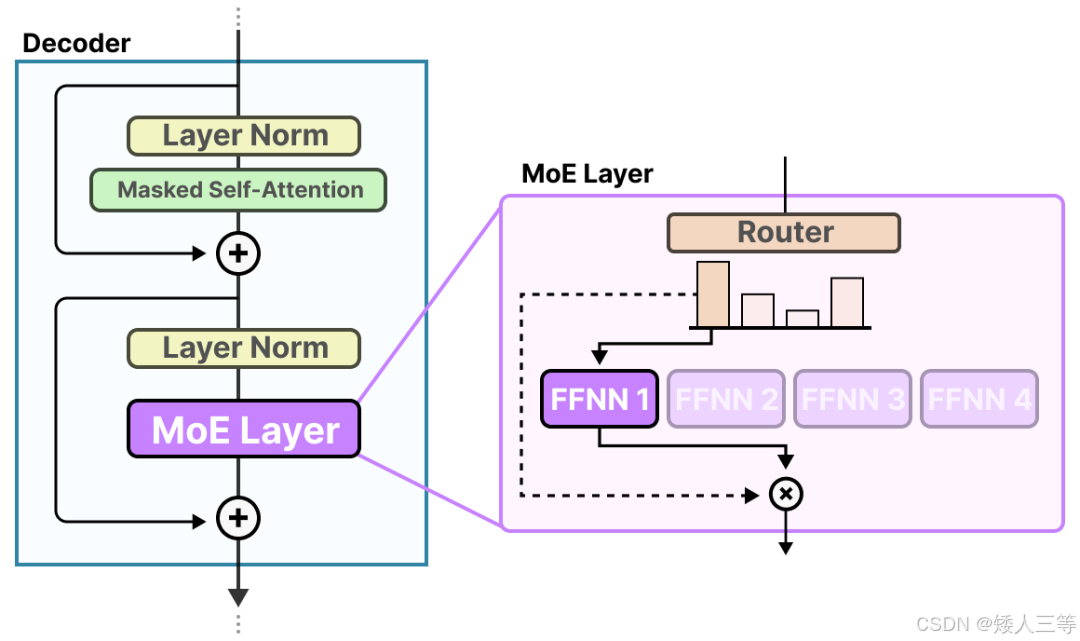
路由器与专家(其中只有少数几个被选中)一起构成了 MoE 层,且完整流程如下
-
路由如何实现选择专家的方法
-
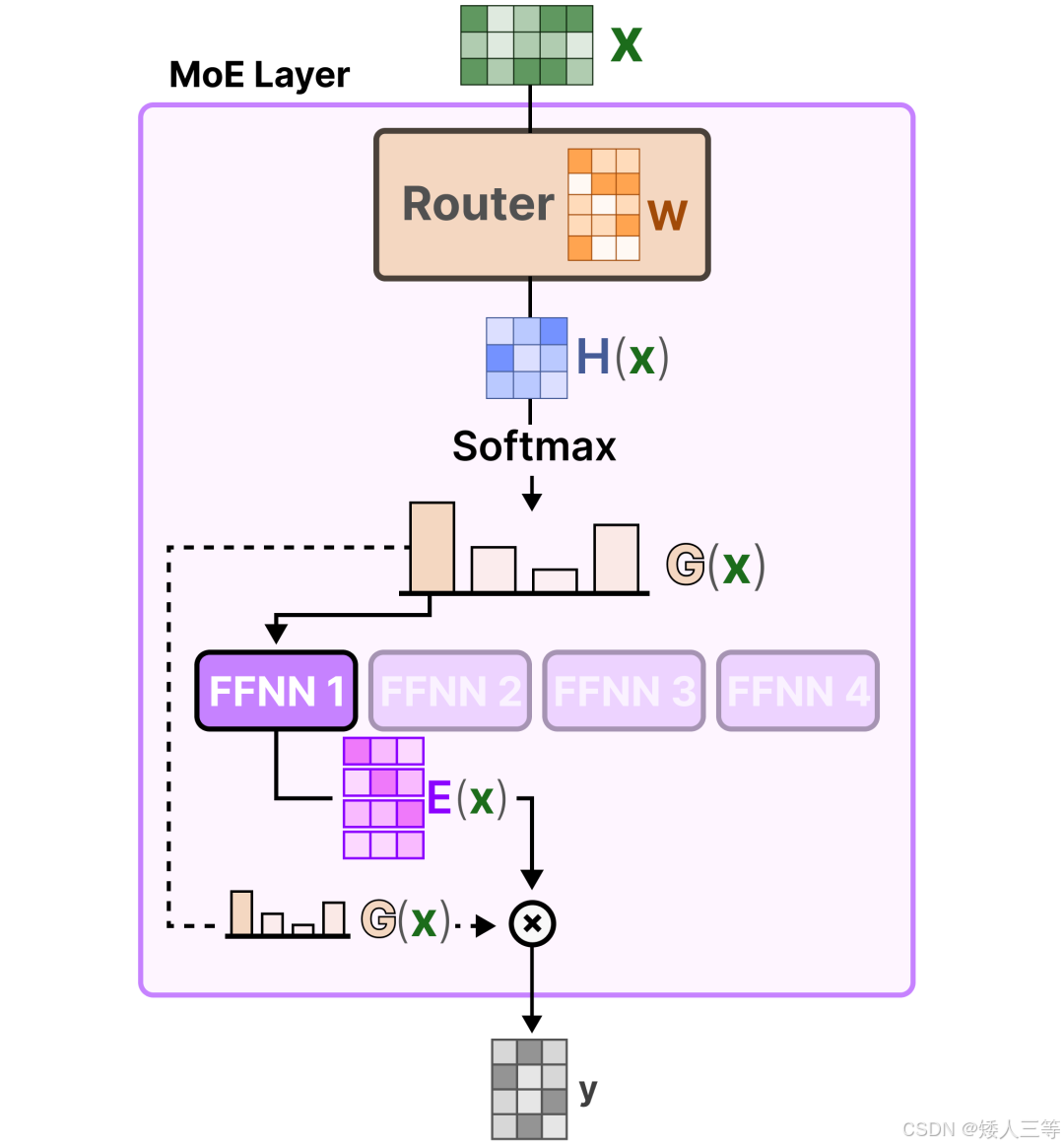
普通 MOE核心规范公式:
-
专家网络:如上 4.1.2 公式所示 ei(x)
-
门控网络(无噪声):logits = W * x + b
- W,b 就是门控网络的权重、偏置(单层线性层,将d_model映射到N维,对应N个专家),x 是输入
- logits 就是N个专家的原始匹配分数(分数越高,越适合处理当前 token)。
-
选 Top-K 专家:ρ = softmax(logits), ρ_i 表示第i个专家的初始权重(代表匹配度概率)
-
得到选中的专家索引:topk_idx = argtopk(ρ, K):K通常为 1 或 2
-
对选中专家重新归一化权重: ρ^topk = ρ_tok / (∑(i∈topk_idx) ρ^mask,i)
- 例如ρ = [0.5, 0.3, 0.2](3 个专家的权重),K=2:
- topk_idx = argtopk (ρ,2) → [0,1](第 0、1 个专家);
- ρ_topk = [0.5, 0.3](原始 Top-K 权重,和为 0.8≠1);
- ρ^topk = [0.5/0.8, 0.3/0.8] = [0.625, 0.375](归一化后和为 1,才能加权融合)。
-
输出加权融合:y = ∑(i∈topk_idx)ρ_i⋅ei(x) ρ^i 是第i个选中专家的归一化权重 ; ei(x):第i个专家的输出。
-
完整 MOE 层输出(含 Add&Norm):y_final = LayerNorm(x + y)
-
基础平衡损失(均方误差型):
- L = ∑ (i = 1~ N ) (Fi - 1 / N) ^2
- Fi = 1 / B * ( ∑ (j=1~ B) || (i∈topk_idxj))
- B:Batch 大小(一批处理的 token 数);
- ||(⋅):指示函数(专家i被选中则||函数结果为 1,否则为 0);
- Fi:专家i在当前 Batch 中被选中的频率;
- 1 / N :理想的均匀选中频率(每个专家被选概率均等)
- 均方误差属于辅助平衡损失,主损失还是任务类型决定的损失,比如分类的交叉熵损失
-
基础 MOE 结构的缺陷:
- 专家负载不均:门控易偏好少数专家,其他专家闲置(基础平衡损失效果有限);
- Token 扎堆:所有 Token 都选少数专家,导致这些专家计算过载;
- 门控打分模糊 / 极端:要么权重太平均(分工不明确),要么 logits 爆炸(梯度消失);
- 分布式扩展难:专家多了之后,无法高效分布到多 GPU/TPU(基础 MOE 只是设计之初没考虑并行,不是不能并行);
- 计算冗余:K=2 时仍有部分计算浪费,推理速度不如稠密模型。
text例子:基础 MOE(K=2,无噪声 / 并行,均方平衡损失) 主任务:简单文本分类(Lmain为交叉熵损失); 专家结构:每个专家是简单 FFN(ei(x)=W2(i)⋅GELU(W1(i)⋅x),W1/W2为随机初始化的 2×4/4×2 矩阵)。 专家数N=4(E1/E2/E3/E4),输入 Token:T1=[1,2], T2=[3,4] 门控打分: T1 的 logits = W*T1+b=[0.8,0.6,0.3,0.1] → ρ1=softmax([0.8,0.6,0.3,0.1])=[0.4,0.3,0.2,0.1]; T2 的 logits = W*T2+b=[0.2,0.7,0.5,0.4] → ρ2=softmax([0.2,0.7,0.5,0.4])=[0.1,0.4,0.25,0.25]; 选专家: T1 的 topk_idx=[0,1] → ρ^1,topk=[0.4/(0.4+0.3),0.3/(0.4+0.3)]=[0.571,0.429]; T2 的 topk_idx=[1,2] → ρ^2,topk=[0.4/(0.4+0.25),0.25/(0.4+0.25)]=[0.615,0.385]; 专家计算: T1 激活 E1/E2 → e1(T1)=[0.5,0.6],e2(T1)=[0.7,0.8]; T2 激活 E2/E3 → e2(T2)=[0.9,1.0],e3(T2)=[1.1,1.2] 加权融合: T1 的y1=0.571×[0.5,0.6]+0.429×[0.7,0.8]=[0.586,0.686]; T2 的y2=0.615×[0.9,1.0]+0.385×[1.1,1.2]=[0.977,1.077]; 残差归一化: y1,final=LayerNorm(T1+y1)=LayerNorm([1.586,2.686]); y2,final=LayerNorm(T2+y2)=LayerNorm([3.977,5.077]); 训练损失: 主损失Lmain=交叉熵(y_final,标签)=0.8; 平衡损失:f1=0.5(E1 只被 T1 选),f2=1(E2 被 T1/T2 都选),f3=0.5(E3 只被 T2 选),f4=0(E4 没被选); L_balance=(0.5−0.25)2+(1−0.25)2+(0.5−0.25)2+(0−0.25)2=0.0625+0.5625+0.0625+0.0625=0.75; 总损失L_total=0.8+0.1×0.75=0.875(λ=0.1); 反向传播:更新门控 + 选中专家的参数,E4 无梯度(未激活)。
-
-
GShard:在基础 MOE 上的增量优化(解决「负载不均 + 分布式扩展 + 分工模糊」)
-
依然是计算每个专家原始匹配分数(logits_n 带噪音的 logits): logits_n = W * x + b + ε
- ε 为随机噪声,一般服从高斯分布或者均匀分布,加入噪声是为了
- 推理阶段:噪声门控退化为普通 TopK,即ε为 0,KeepTopK 也就退化成了普通的 TopK
-
选 Top-K 专家:ρ^noisy = softmax(logits_n), ∑i ρ_i 表示第i个专家的初始权重(代表匹配度概率)
-
得到选中的专家索引: topk_idx = argtopk(ρ^noisy,K)
-
KeepTopK 核心:生成掩码,仅保留选中专家的权重,其余置 0,即Mask_i = 1 当 i ∈topk_idx 的时候,如果不属于则为 0,得到 ρ^mask = ρ^noisy ⊙ Mask_i ⊙表示矩阵对应位置相乘,不是矩阵乘法
-
归一化保留的权重: ρ^topk = ρ^mask / (∑i∈topk_idx ρ^mask,i)
- ρ^topk:被选中的专家的重新归一化权重(和为 1,避免权重稀释,确保融合结果有效)
-
GShard 熵型负载均衡损失(替代基础 MOE 的均方误差损失)
- L_gshard =- 1 / N ∑ (i = 1~ N ) Fi * ln(Fi)
- 原理:样本分散程度越大,熵越大,专家选中频率越均匀;损失最小化时,fi→1/N,负载完全均衡,通俗理解就是你得到的 fi 的值分布越均匀,L_gshard 的绝对值越大,但是L_gshard损失越小(负数)
- 解决问题:基础均方误差损失不平滑,专家负载仍不均衡
-
门控熵损失(基础 MOE 无,GShard 新增)
- L_entropy = - 1 / B * ( ∑ (j=1~ B) (i = i ~ N ) ρ^ij * ln(ρ^ij))
- ρ^ij: 第j个 Token 对第i个专家的权重;
- 原理:损失越小,门控对每个 Token 的专家权重越集中(比如只给 Top-K 高权重),分工更精准。
- 解决问题:门控权重太平均,专家分工不明确
-
总损失 L = L_main + λ^g * L_gshard + λ^e * L_entropy
- L_main 是主任务的损失,不是均方损失,那是辅助平衡损失
- λ两个超参数是用来平衡这两个损失的
-
Expert Choice 专属 Token 均衡损失(基础 MOE 无)
- 若用「专家选 Token」:L = ∑(i = 1 ~ N) (Ci / B - 1 / N)^2
- Ci:专家i选中的 Token 数;
- 解决:专家选 Token 时,避免少数专家选走大部分 Token。
- Expert Choice(专家选 Token): 反向让专家主动挑适合自己的 Token,替代「Token 选专家」解决选专家不均衡的问题
-
8 和 9 的区别在于 8 适用通用场景,Token 主动选专家,9 是Token 扎堆选少数专家时,反向让专家挑 Token
- token 选专家:1. Token 数量少(<10 万);2. 专家数量多(>8);3. 负载相对均匀; 4.分类任务(Token 少)用 Token 选专家。小规模 MOE
- 专家选 token:. Token 数量多(>100 万);2. 专家数量少(≤8);3. Token 扎堆选少数专家(负载不均);4. 分布式训练(多 GPU);5生成任务(Token 多)用专家选 Token
-
总结优化方向:
- 加噪声让门控「多试试不同专家」;
- 让专家「主动挑 Token」,避免 Token 扎堆;
- 用熵型损失让负载均衡更平滑,用熵损失让门控「选得更准」;
- 加专家并行,让 MOE 能扩展到万亿级参数
text复用基础 MOE 的基础信息,只显示增量示例过程 噪声门控(训练阶段): T1 的 logits_noisy = [0.8,0.6,0.3,0.1] + [0.05, -0.02, 0.01, -0.03]( 高斯噪声ε∼N(0,0.01))→ [0.85, 0.58, 0.31, 0.07]; T1 的ρ1,noisy=softmax([0.85,0.58,0.31,0.07])=[0.42,0.29,0.2,0.09]; T1 的 topk_idx=[0,1](仍选 E1/E2,但权重略有变化); 专家并行部署: E1→GPU1,E2→GPU2,E3→GPU3,E4→GPU4; T1 的计算:T1→GPU1(E1)+ GPU2(E2)→ 结果汇总到主 GPU; T2 的计算:T2→GPU2(E2)+ GPU3(E3)→ 结果汇总到主 GPU; 熵型平衡损失(替代均方损失): f1=0.5,f2=1,f3=0.5,f4=0; L_balance_GShard=−1/4(0.5log0.5+1log1+0.5log0.5+0log0)=−1/4(−0.3466+0−0.3466+0)=0.1733 门控熵损失: T1 的ρ1,noisy=[0.42,0.29,0.2,0.09] → 熵H1=−(0.42log0.42+0.29log0.29+0.2log0.2+0.09log0.09)=1.25; T2 的ρ2,noisy=[0.11,0.39,0.26,0.24] → 熵H2=1.3; L_entropy=−1/2(1.25+1.3)=−1.275(取负后损失为 1.275); 总损失: Ltotal=0.8+0.1×0.1733+0.05×1.275=0.8+0.0173+0.0638=0.8811; 核心效果:噪声让 E4 有概率被选中(比如 T1 的ρ1,noisy中 E4 权重从 0.1→0.09,仍低但非 0),熵损失让门控权重更集中,专家并行提升计算速度。
-
-
Switch Transformers: 在基础 MOE/GShard 上的极简增量优化(解决「计算冗余 + 训练不稳定 + 超大规模效率」)
-
基于基础 MOE 的方法,下面主要列出改动的地方
-
topk_idx = argtopk(ρ,1) (仅选1个专家)
-
y=ρ_i⋅ei(x)(仅1个专家的输出,无求和)
-
Switch 专属平衡损失(替代基础 / GShard 的平衡损失,K=1 专属)
- L_balance = N / B^2 * ∑(i=1~N) Ci ^ 2 −1
- Ci:专家i被选中的 Token 数(K=1 时,Ci就是专家i处理的 Token 总数);
- 原理:理想状态Ci=B/N,代入后L_balance=0;损失最小化时,所有Ci相等,负载完全均衡
-
Z-loss(Switch 专属,基础 / GShard 无)
- Lz = 1 / B * ∑(j=1~B) || logits_j || _2^2
- logits_j:第j个 Token 的门控原始 logits;
- ∥⋅∥:范数 (衡量向量的 "长度 / 大小"),∥⋅∥2是L2 范数(欧几里得距离);
- 第一个 2:表示 L2 范数(最常用的范数);
- 第二个 2:表示对 L2 范数取平方(简化计算,效果和 L2 范数一致)。
- 原理:把 logits 的尺度压在合理范围, logits 过大导致 softmax 后权重趋近 0/1,梯度消失。。
-
Switch 总损失: L = L_main + λ^b * L_balance + λ^z * Lz
-
总结优化内容:
- 把 K 改成 1,每个 Token 只找 1 个专家,推理速度接近稠密模型,显存占用大幅降低;
- 用专属平衡损失,让 K=1 时专家负载更均匀;
- 加 Z-loss,解决门控 logits 爆炸的训练稳定性问题;
- 极简并行设计,让万亿级 PaLM 模型能高效训练 ------解决了基础 MOE 的计算冗余、训练不稳定、超大规模效率低。
-
通俗比喻思路就是:门控负责挑 "最适合Token的 1 个专家",Switch 损失强制要求每个专家的处理的 token 数量差不多,Z-loss防止专家打分太极端,导致误判 toekn 的最优最优专家。
text依旧基础假设信息同基础 MOE Switch FFN(K=1): T1 的ρ1=[0.4,0.3,0.2,0.1] → topk_idx=[0](仅选 E1); T2 的ρ2=[0.1,0.4,0.25,0.25] → topk_idx=[1](仅选 E2); 归一化:ρ^1,topk=1(仅 1 个专家,权重为 1),ρ^2,topk=1; 融合:y1=1×e1(T1)=[0.5,0.6],y2=1×e2(T2)=[0.9,1.0]; Switch 平衡损失(K=1 专属): C1=1(E1 被 T1 选),C2=1(E2 被 T2 选),C3=0,C4=0; L_switch_balance=4/(2^2) *(1^2+1^2+0^2+0^2)−1=2−1=1; Z-loss(防 logits 爆炸): T1 的 logits=[0.8,0.6,0.3,0.1] → ∥logits1∥_2^2=0.8^2+0.6^2+0.3^2+0.12=0.64+0.36+0.09+0.01=1.1; T2 的 logits=[0.2,0.7,0.5,0.4] → ∥logits2∥_2^2=0.04+0.49+0.25+0.16=0.94; Lz=1/2*(1.1+0.94)=1.02; 总损失: Ltotal=0.8+0.1×1+0.05×1.02=0.8+0.1+0.051=0.951; 核心效果:K=1 让计算极简(无需加权求和),Switch 损失保证 E1/E2 各接 1 个 Token(负载均匀),Z-loss 把 logits 长度压在 1 左右(避免爆炸)。
-
存在的挑战
- 训练挑战: 虽然 MoE 能够实现更高效的计算预训练,但它们在微调阶段往往面临泛化能力不足的问题,长期以来易于引发过拟合现象。
- 推理挑战: MoE 模型虽然可能拥有大量参数,但在推理过程中只使用其中的一部分,这使得它们的推理速度快于具有相同数量参数的稠密模型。然而,这种模型需要将所有参数加载到内存中,因此对内存的需求非常高。以 Mixtral 8x7B 这样的 MoE 为例,需要足够的 VRAM 来容纳一个 47B 参数的稠密模型。之所以是 47B 而不是 8 x 7B = 56B,是因为在 MoE 模型中,只有 FFN 层被视为独立的专家,而模型的其他参数是共享的。此外,假设每个令牌只使用两个专家,那么推理速度 (以 FLOPs 计算) 类似于使用 12B 模型 (而不是 14B 模型),因为虽然它进行了 2x7B 的矩阵乘法计算,但某些层是共享的。
补充
- 使用 MOE 结构的主流大模型:
- Mixtral 8x7B:8 个专家,每个专家 7B 参数,K=2(每个 token 激活 2 个专家)
- DeepSeek MoE:16 个专家,引入 "共享专家"(所有 token 都激活的专家)
- Llama 4 MoE:采用动态专家数量,优化负载均衡
- 关键变体:
- 共享专家:在 MoE 层中加入少量共享专家(如 1-2 个),所有 token 都会激活这些专家
- 作用:提供基础能力,防止冷门问题没有专家处理
- MoE-Layer Placement:不是所有 FFN 层都替换为 MoE 层,而是在关键层使用(如 Llama 4 MoE 在中间层使用)
- MMoE(Multi-gate Mixture-of-Experts):多任务学习场景,每个任务有独立的门控网络
- 共享专家:在 MoE 层中加入少量共享专家(如 1-2 个),所有 token 都会激活这些专家