《智能的理论》全书转至目录****
不同AGI的研究路线对比简化版:《AGI(具身智能)路线对比》,欢迎各位参与讨论、批评或建议。
一.概述
在现实世界中,客体通常并非孤立存在,而是多个客体共存。除了认识各个独立客体之外,对客体间关联性的处理是人们准确、有效地认识和探索世界的关键。其中,视觉构型是最重要的客体间关系之一。
视觉构型的常见应用场景涵盖静态场景、动态场景以及客体的内部构型。在静态场景中,各客体的位置相对固定,例如家庭中的家具与电器。然而,日常生活中,动态的视觉场景同样普遍存在,从古代追逐猎物到现代与队友踢足球,大脑必须动态地处理各客体在空间中的关系。许多客体内部都包含一些子客体,例如脸孔中的子客体包括眼睛、嘴巴、鼻子和耳朵等,房子的子客体则包括门、窗和屋檐等。当子客体之间形成某种特定的空间关系时,这种构型能够有效辅助对该客体的识别。如在面孔识别中,构型发挥着至关重要的作用(9-20:面孔识别)。
众多研究表明,相较于单独记忆客体位置,当客体与其他客体形成空间关系时,记忆效果显著提升。Olson和Chun(2000)在其实验中发现,记忆中颜色方块的位置信息并非孤立存储,而是与客体属性共同编码。当该方块与其他位置的方块同时呈现时,其位置回忆效果得到增强。这种由多个客体空间位置所构成的整体被称为客体构型,它揭示了多个客体在空间记忆中的组织关系。
二.构型的层级结构
几何学理论将构型结构划分为几个不同的层次(Chen,2005),这些构型层次有不同的抽象程度或者具体程度。主要包括以下几种:
1.全等构型
全等构型就是客体组合自身在空间中的布局,没有进行任何空间变换,保留空间结构的所有信息;
2.仿射结构
仿射结构即在仿射变换中结构所保留的空间信息。平移、旋转、缩放、拉伸、反转,以及这些变换的任意组合都属于仿射变换。用数学的语言表达为

其中,x和y为变换前的坐标,x'和y'为变换后的坐标,Tx和Ty为平移因子,R为线性变换因子,它决定结构的旋转、缩放、拉伸和反转等,如例1。
例1
(a)平移

该表达式表示的是对位置(x,y)位移(tx,ty),得到(x',y')=(x+tx,y+tx),如图1。
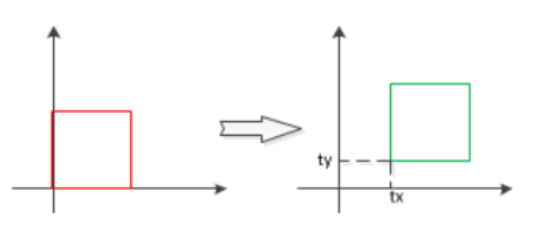
图1
(b)旋转
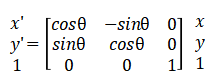
该式子表示对位置(x,y)旋转θ得到(x',y'),如图2。
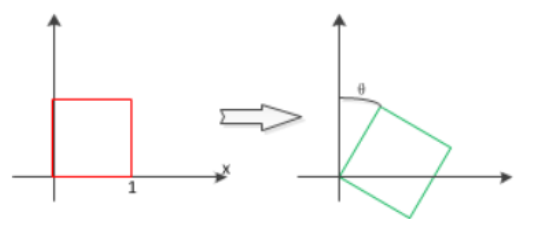
图2
(c)缩放
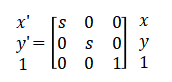
该式子表示对位置(x,y)缩放s倍(当s大于1时为放大,当s小于1时为缩小,当s等于1时变换前后两个构型没有发生任何变化,即全等结构,因此全等结构是仿射结构的一个特例),如图3。
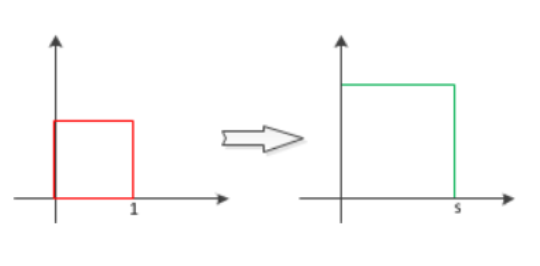
图3
(d)仿射不变性
仿射不变性是指在仿射变换下,一个图形的某种性质或量保持不变的特性。在仿射变换中角度、距离和面积等可以发生变化,但会保留其他性质,如拓扑性(如原来相邻的点变换后还是相邻,并且原来多少区域变换后还是多少区域("8"型有两个区域,"0"型只有一个区域,因此它们之间没有拓扑性))、平直性(直线在仿射变换后仍然是直线)、平行性(平行线在变换后仍然是平行线)、共线比例不变性(变换前一条线上两条线段的比例,在变换后比例不变)和凸性(一个凸多边形在仿射变换后仍然是凸多边形,但不能变换为凹多边形)等。例如,一个正方形可以通过仿射变换变为任何类型的矩形,甚至是平行四边形,但不能变为梯形(正方形、长方形和平行四边形具有相同的仿射结构,它们之间的变换属于仿射变换。但由于梯形与正方形不满足平行性,因此正方形与梯形没有共同的仿射结构,它们之间不能通过仿射变换得到)。
3. 射影结构
射影结构,即在射影变换中结构所保留的空间信息。仿射变换有很多限制(即它的性质,如平直性、平行性等),而射影变换在此基础上解除了很多限制而引入了更多的变化。如没有平行性,但保留了一些更基本的性质,如拓扑性、平直性和凸性。在射影变换下,一个凸多边形在射影变换仍然为凸多边形。
射影变换的直观例子如图4,蓝色平面上的圆形和黄色平面上的椭圆形之间的变换就是射影变换,其中P点称为投影中心,投影中心及两个平面之间三者的相对方位可以任意变换。射影变换在生活中是很重要和常见的,如图5(a),其中视点(即眼睛)为投影中心,它使水平地面的像与垂直视平面的像(图(b))形成射影变换,该变换使水平地面上的平行铁轨(图(a)灰色平行线)变换为视平面上相交的两条线。
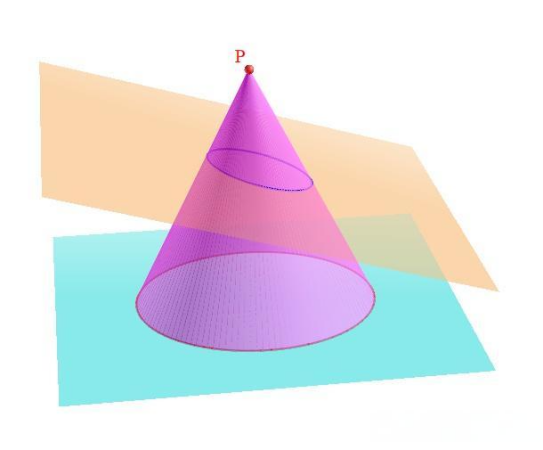
图4
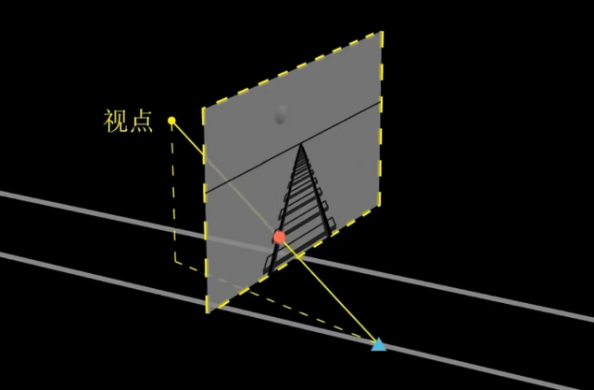
图5(a)
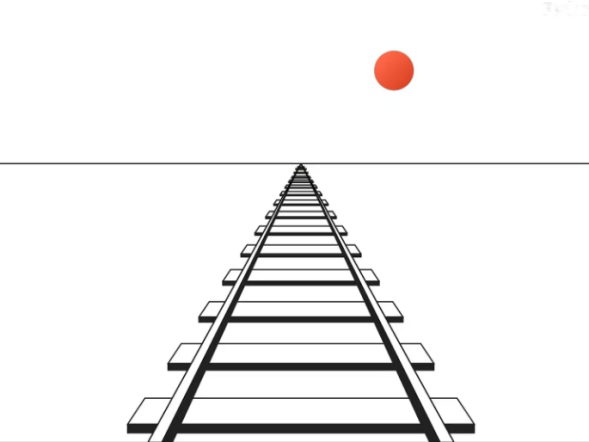
图5(b)
射影变换用数学的语言表达为

其中,Tx和Ty为"xy平面"上的平移因子,R为"xy平面"上的线性变换因子,而最后一排为射影变换因子,它使二维坐标(x,y)转变为三维坐标(x',y',z')。当a31=0、a32=0和a33=1时,射影变换变为仿射变换,可见仿射变换是射影变换的一种特殊形式。
4.拓扑结构
拓扑结构,即拓扑变换中结构所保留的空间信息。相比射影变换,拓扑变换更为激进,如没有了原来的凸性,凸边型经过拓扑变换可以转变为一些凹边型,但拓扑结构保留了其拓扑性,包括:联通性、联通域个数、相邻关系、内外关系、开放性与封闭性等。作为一个连通整体的性质就是联通性,一个三角形变成正方形或圆后,其连通性保持不变,因此它们之间的拓扑结构没有发生变化。但如果一个三角形分裂为多个形状,那么联通性会被破坏;连通域个数不变时,其拓扑结构不变;反之则会改变。比如由"0"型变"8"型时拓扑结构改变(联通性没变,但从一个连通域变为两个连通域);当相邻关系被打破,拓扑结构也会发生改变,如对于无环图"A-B-C",A与B相邻,B与C相邻,但是C与A不相邻,当这个无环图变为"A-C-B"时拓扑结构发生改变;内外关系,即一个物体与另外一个物体的内外关系(是否在内部),如一个圆形连续变形为一个椭圆形,原来圆形区域的内部点在变形后依然是椭圆形区域的内部点,它们之间拓扑关系不变;开放性即一个区域是没有界限的(如一个"十字"),而封闭性则有其界限,它们是一对的拓扑性质,拓扑变换后其开放性或封闭性保留。(邓小凤,袁颖,李富洪和李红,2013;Chen,2005)
根据陈霖等人(陈霖,朱滢和陈永明,1996)的研究,拓扑性质的知觉加工先于局部几何性质的知觉加工,即先有拓扑不变性质的把图形和背景相分离的早期辨别,然后才有可能对图形的局部几何性质进行加工。
5.非拓扑结构
非拓扑变换是最为激进的变换,这种变换不属于上述任何一种变换,它打破了上述不变性的全部限制,包括拓扑性。
6.小结
这5种构型信息用下面的图6做一个小结,图中左边为变换前的原构型,而右边分别为经过四种变换得到的构型,分别是,仿射变换、射影变换、拓扑变换和非拓扑变换。图(a)作出了旋转和缩放;图(b)在变换前后保持了凸性,是射影变换但不是仿射变换;图(c)四个点从凸多边形转变为凹多边形,因此不是射影变换,但这种变换保留了其拓扑性(如各圆点的相对位置没有发生变化并且区域数量不变),因此是拓扑变换;图(d)其中一个点穿过其对角的边缘,因此要么从凸多边形变为自相交的凸多边形,区域从一个变为两个(联通域个数改变,因此拓扑结构发生变化),形成了新的四边形但各点的相对位置发生了变化(相邻关系发生变化,因此拓扑结构发生变化),因此该变换为非拓扑变换。
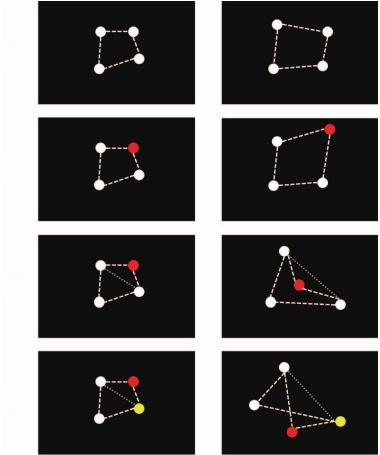
图6
三.编码
1.构型层次
相比单独记忆客体位置,当记忆客体与其他客体形成空间关系时记忆效果更好。这是因为被试在任务中使用了记忆客体在构型结构中的信息。现在的问题是,不同构型信息对记忆任务的影响如何呢?一种假说是连续衰减假设,该假设声称所有类型构型结构都参与构型记忆任务。但随着从仿射到非拓扑不同层次的变换,结构逐渐被扭曲被打破,构型对任务的影响单调下降;另一种是突然崩溃假设,该假设声称视觉系统在低于或等于某个层级的构型结构时成绩不变,低于或等于该级别的任何变异都可以容忍,不会对任务成绩造成任何下降,而高于该级别的任何变异会造成成绩的突然下降。这种层级特性也被称为该层级的几何不变性,显然层级不变性是向下兼容而不向上兼容的,比如在射影变换中具有几何不变性,那么在仿射变换中也具有,但是拓扑变换没有。另外一个问题是,如果突然崩溃假设是正确的,需要判断几何不变性到底是在哪个层级?(Sun,Huang,Yu和Zhang等人,2015)
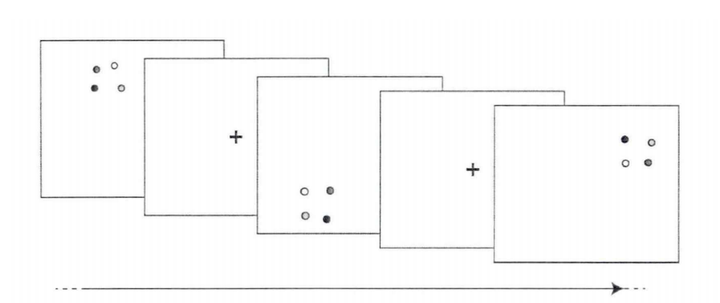
关于此问题,Sun等人对此进行了研究。他们的实验如图7所示,在每个试次中,第一步,显示一个白色注视十字500ms;第二步,呈现四个随机放置的四个白色点,持续500ms;第三步,四个点向随机方向运动500ms作为学习刺激:第四步,小点停止运动并保持1000ms;第五步,这些点再次移动500ms作为测试刺激。在50%的试验中,学习刺激的移动方向与测试刺激的相同。在其余的50%试验中,测试刺激其中一个点的移动方向与学习刺激的方向相比顺时针或逆时针改变45°,该点称为关键点。在该实验中,研究人员假设在被试视觉系统中这些点形成了一个"多边形",即构型。这些构型如图6,其中细虚线表示为多边形的对角线,大虚线表现为多边形的边(这些虚线在实验中均没出现,仅用于表示客体构型),红点表示关键点。

图7
实验的关键在于,使用了不同层级的构型信息,即通过点运动给使原来的构型变换为另外一种构型,如图6的左图通过移动变为其右图(同一行)。其中,在图(d)中,关键点先接近对角线,然后穿过它。实验结果显示,从仿射到非拓扑变换,原结构逐渐被扭曲被打破时,构型的稳定性不是单独调下降(因此否定了连续衰减假设),而是在拓扑变换时断崖式下降(因此支持了突然崩溃假设),且仿射变换和射影变换的成绩相当,拓扑变换与非拓扑变换相当。另外,在Jiang等人(Jiang,Olson和Chun,2000)的研究中发现,全等构型与射影结构的任务成绩一致而非减弱(9-28:视觉工作记忆)。
因此,综合上述研究,其结果支持突然崩溃假设,并且视觉系统拥有的是射影结构的几何不变性。由于人眼视觉(世界到视平面)就是一个射影变换,因此视觉系统的这种特性有利于人们视觉输入的稳定性。比如,看书的时候由于头部运动或者书本转动,书本的矩形输入可能会变为一个梯形输入,但是人们的知觉还是矩形,如图8。
图8
2.方向依赖
我们的知觉系统具有射影不变性,因此也具有仿射不变性(向下兼容)。旋转属于一种仿射变换,因此当构型旋转时,被试应该能稳定感知(旋转后任务成绩不变)。然而,在黄羽商(2018)的一个实验中却得出了相反的结论。
每个客体有其自身的特征(颜色、形状等),也有与其他客体结合的构型特征。黄羽商(2018)在其实验中分离了这两类特征。学习阶段刺激的四个圆分别位于屏幕四个象限的随机位置(图9(a))。测试阶段可能会对学习阶段的刺激作出两种变化,第一种是圆点可能在各自象限内作一定位移,没移动的条件称为原形态,移动了的条件称为新形态。第二种是圆的位置不变,但是颜色可能会延顺时针方向或者逆时针方向旋转90度,如使颜色顺时针旋转,原来第1、2、3、4象限的颜色会分别换到2、3、4、1象限的圆中(构型的形状、朝向和位置均没发生变化,只是颜色变了)。颜色没旋转的条件称为方向不变,旋转了的条件称为方向变化。"形态"和"方向"这两个维度组合成4种情况,"原形态-方向不变"、"原形态-方向变化"、"新形态-方向不变"和"新形态-方向变化",如图9(b)所示。实验中先呈现学习刺激,经过一段时间的空屏后得到测试刺激。被试需要判断相比学习刺激,测试刺激中是否有一个小球的颜色发生变化。结果显示,方向的维度对成绩的影响较大,即方向改变时,被试的成绩变差。而形态的维度对成绩的影响不大。四种条件的测试成绩总结可表示为"原形态-方向不变"≈"新形态-方向不变">"新形态-方向变化"≈"原形态-方向变化"。
在该实验中,新形态可以视为在原构型上的射影变换,其射影结构不变。相比"原形态-方向不变"(全等构型),"新形态-方向不变"的成绩没有变低,因此,再次证明构型在视觉处理中具有射影不变性。对于"方向变化"造成的成绩降低,有两种可能的解释,第一种可能的解释是,方向变化条件可以看成两步,先对各点(包括构型和颜色)同时旋转,然后各点再移动(射影变换)。其中,"原形态-方向变化"的第二步(射影变换)只是刚刚好变回原形态。因此怀疑是方向依赖造成的成绩变低。第二种可能是,由于实验使构型特征与颜色特征分离,这两种特征发生冲突,从而造成成绩的降低。到底是"方向依赖"还是"特征冲突",这个问题将会在第二个实验中得到解决。

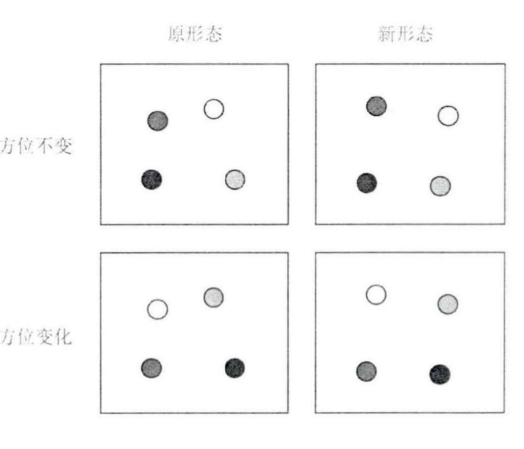
图9
在黄羽商(2018)的第二个实验中增加了一个维度,即构型旋转。当构型旋转时,颜色的象限位置可以保持不变,即仅构型发生旋转,而颜色保留在原象限;或者颜色跟随圆点客体一起旋转(几何一致)。该实验包含三种测试刺激,"原形态-方向不变"、"构型旋转-方位不变"和"构型旋转-几何一致",如图10。结果表明,"原形态-方向不变"≈"构型旋转-方位不变">"构型旋转-几何一致"。在该实验中,"构型旋转-方位不变"的成绩并没有降低,因此排除特征冲突的假设;相反"构型旋转-几何一致"是完全通过圆点的旋转变换所得(构型和颜色同时旋转),因此证明在构型信息的视觉系统处理中存在方向依赖,如物体识别和空间识别的视角依赖一样("9-19:图像识别"和"11-3:空间坐标")。
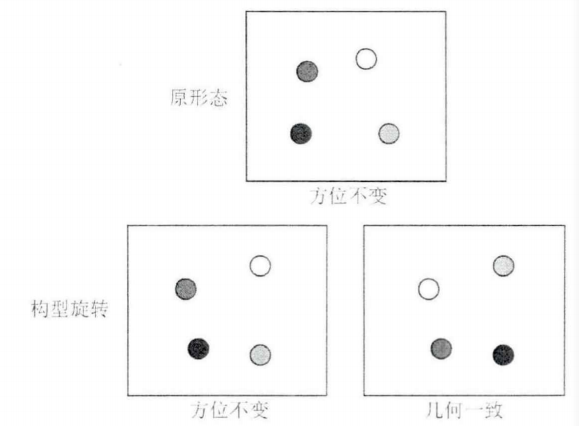
图10
3.子构型与参照系(定位)
记忆客体与其他客体形成空间构型时相关任务成绩更好,那子构型呢?黄羽商(2018)使用了4个客体圆构成的构型(即一个四边形)作为研究对象。其子构型由其其中的3个圆点构成(即一个三边型),如图11。在实验中,学习阶段呈现4个圆作为学习刺激,而在测试阶段测试刺激可以有两种情况,一种是测试刺激是包含4个圆点的刺激,而另外一种是只保留其中3个圆点。实验结果表明,展示4个圆的成绩要优于3个圆的。
对于该结果,是否表明在构型编码中并不包含其子构型?研究者认为,当其中一个客体消失时(只显示3个圆),被试可能没有意识到该构型是学习刺激构型的子构型,而认为是一种新构型的存在。在随后的实验中,实验者在屏幕的原点中添加了"+"号,它是学习刺激的构型中心,如图12所示。前者(无"+"号)与后者(有"+"号)相比,由于没有"+"号的提示,当缺少一个客体时,新构型(三角形)的中心位置发生了变化(不在原点了),因此各客体相对于原构型中心的相对位置发生了变化。而后者有了"+"号的提示,即使缺少了一个客体,剩余三个客体与原构型中心的相对位置没有发生变化(还处于原点中),因此在测试过程中保留了原构型的子构型信息(而非作为一个全新的构型)。在添加"+"号的实验中验证了这个猜想,结果显示4个圆的成绩要与3个圆(子构型)的相似。
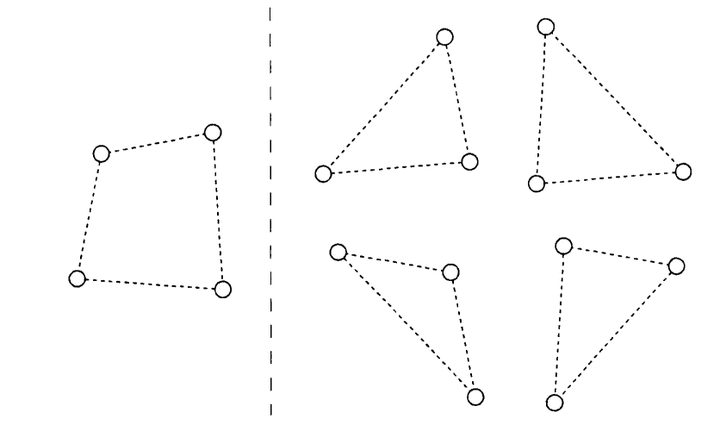
图11
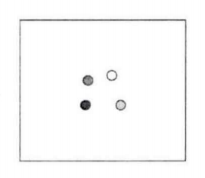
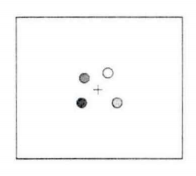
图12
4.客体之间的空间关系
Jiang和Wagner(2004)利用实验证明了客体之间的空间关系(非构型信息)也有助于对目标客体的定位,如时钟与黑板右上角相距0.5米,相对方向为45度,当找到黑板右上角时就很容易对时钟定位。该研究还发现,客体方位信息编码的是相对位置而非绝对位置,比如两客体仅距离增加而方向不变时,成绩没有显著降低。
5.客体数量
Papenmeier等人(Papenmeier,Huff和Schwan,2012)对客体数量对构型信息的影响进行了研究,该研究分别在静态场景和动态场景中进行了实验。结果发现无论是静态场景还是动态场景,6客体同时呈现条件(6个客体组成的构型)的绩效都远远优于其他两种数量条件(呈现3个客体、仅只呈现1个目标客体)。
6.任务
事实上,射影不变性并不对所有任务都适用。射影不变性可能只是代表了一种普遍性,但在一些任务中可能存在着其特殊性。以人脸识别为例,虽然在判断是否人脸的任务中,所有人脸的构型存在射影不变性。但是仅凭射影不变性无法作出人脸识别(判断具体是哪个人)。在人脸识别中,全等构型才是最重要的。如不同人之间眼睛间的距离是不同的,每个人的眼睛的相对位置都是相同的,仅凭借双眼的相对位置无法识别人脸(9-20:面孔识别)。
7.拓扑关系
事实上,拓扑关系对构型知觉也有重要作用。皮亚杰的拓扑首位理论认为儿童的空间概念发展顺序为先发展拓扑几何,之后再发展其他几何。在4岁之前儿童的空间概念是拓扑学的,对于这些儿童来讲,物体的形状、长度、大小还不具有恒常性(它们属于欧式性质)。在触觉-视觉实验中,皮亚杰等人先以触觉的形式呈现一个图形,再以视觉的形式呈现多个图形,要求被试挑选出之前触摸到的图形。实验结果表明,4岁以前的儿童只能再认熟悉图形和拓扑图形,4岁以后的儿童逐渐能识别欧式图形。还有研究发现,4岁之前的儿童可以复制绘画作品中的拓扑性质,如临近性、封闭性等,但不能表现其他几何性质;而4岁半到6岁的儿童能画出样品图形的直线与曲线的差异,之后儿童才能画出更复杂的几何图形。(邓小凤,袁颖,李富洪和李红,2013)
陈霖的拓扑知觉理论与拓扑首位理论在功能层次上具有共同点,该理论认为,人类视觉系统最先知觉到拓扑性质,然后知觉射影性质,再知觉仿射性质,最后知觉欧式性质。该理论强调图形知觉中拓扑结构的优先性。拓扑知觉的优先性包含两层涵义:第一,拓扑知觉先于其他几何知觉;第二,其他几何知觉建立在拓扑知觉基础之上(Chen,2005)。拓扑性质的知觉发生在视知觉的早期阶段,在实验中,研究人员采用了三对图形作为实验刺激,每对图形分别是实心圆和实心正方形、实心圆和实心三角形、实心圆和环,如图13。实验时要求被试注视每对图的中心黑点,每对图呈现5ms。被试的任务是判断刚才呈现的两幅图形是否相同。实验结果表明,视觉系统更敏感于拓扑性质的差异,即对圆和环这组刺激图形的正确报告率(即报告它们是不一样的),要显著高于圆和三角形以及圆和正方形的正确报告率(Chen,1982)。
一项运动竞争技术研究拓扑不变性质和似动现象的关系。实验先后呈现2幅图形刺激,在第一幅中包含一个位于正中的图形,第二幅包含位于两边的与中心等距离的两个图形。通过调节两幅图呈现的时间和两者之间的时间间隔,使被试产生似动知觉。被试的任务是判断中间的图形看起来是向左边的图形运动,还是向右边的图形运动。实验结果表明,被试会倾向于报告中间的图形会倾向于向拓扑结构一致的图形运动。比如第二张图的图形分别是实心正方形和圆环,第一张图是实心圆,但被试报告的是实心圆有向实心正方形运动的倾向。(陈霖,1987)
另外,人类知觉的拓扑不变性还有来自功能性核磁共振研究的发现,似动现象在前颞叶的激活程度也有相似的顺序性,当似动现象发生在两个具有拓扑差异的图形之间,前颞叶的激活最强,射影性质差异的稍弱,仿射性质差异的更弱,欧氏性质差异的激活程度最低(Chen,Zhang和Srinivasan,2003)。

图13
四. 加工
1.心理旋转
视觉系统具有仿射不变性,但是构型的方向依赖性与此相悖。对此的一个解释是,在黄羽商(2018)的实验二中,学习和测试条件下的两个构型并没有展示出旋转的过程,因此被试不一定能意识到它们的旋转关系(旋转仿射变换)。如果被试不能意识到这一点,那么被试可能将测试构型看作是一个新的构型,由此产生方向依赖性。如果在新实验过程中对被试进行提示,让被试意识到测试刺激是由学习刺激通过旋转得来的,结果又如何呢?
与实验二相比,黄羽商(2018)的实验三在学习和测试构型之间增加了构型旋转方向的提示。这种提示可以通过在刺激外围呈现一个方框将其包围,当学习刺激消失后,方框不消失并开始旋转。在测试阶段,如果测试刺激是学习刺激旋转后得到的("构型旋转-几何一致"条件),且方框旋转的方向与学习刺激旋转方向一致。实验结果显示,添加了提示后的3种情况的成绩类似,即"原形态-方向不变"≈"构型旋转-方位不变"≈"构型旋转-几何一致"。这表明,当被试产生构型旋转的心理操作时,可以保持视觉系统的仿射不变性。
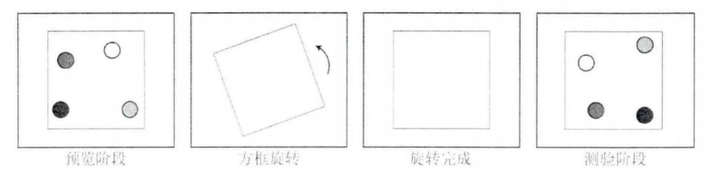
图14
2.镜像操作
(水平)镜像变换是指图像的左右部分以图像垂直中轴线为中心进行镜像对换,比如人在照镜子时,身体左侧的形象会呈现在镜子的右侧,而右侧的形象呈现在左侧。为了研究镜像操作对构型的影响,实验者使用了两种操作条件。一种是中央呈现,即刺激始终在屏幕的中心。另外一种是对侧呈现,即在学习阶段,刺激呈现在屏幕的左侧,而在测试阶段,刺激的镜像呈现在屏幕的右侧。测试刺激的形状(即四个圆点形成的构型)与学习刺激的互为镜像。而它们之间的颜色关系分为3种情况,第一种是颜色的方位不变(即颜色不跟随着形状的镜像变化而变化),第二种是随机变化,第三种是颜色跟着形状一起变化,如图。实验结果表明,在中央呈现条件,仅有颜色原方位情况的构型信息得到有效利用。而在对侧呈现条件,颜色原方位和颜色镜像方位的构型信息都得到有效利用。这表明,对侧呈现起到一种线索作用,使被试产生了对学习刺激的镜像操作。(黄羽商,2018)
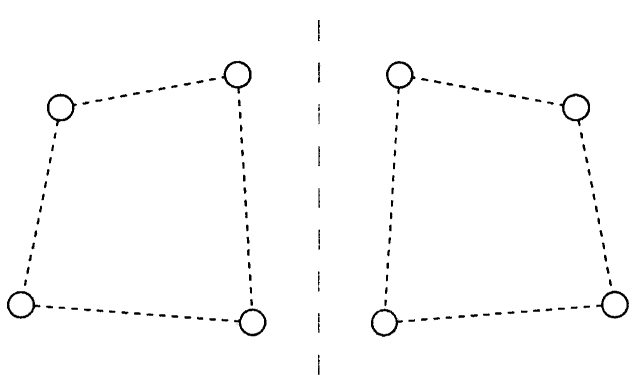
图15
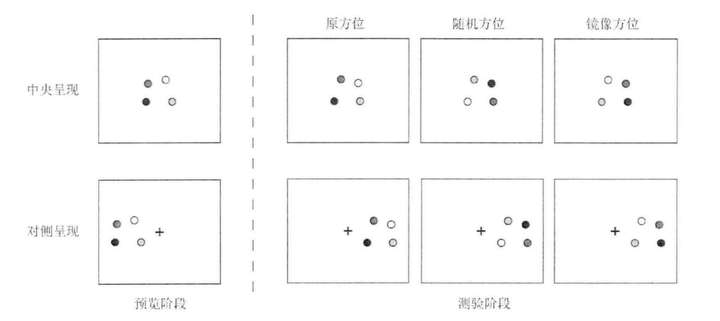
图16
3.构型变换的注意力分布
叶艳(2012)采用点探测任务对构型破坏时(非拓扑变换)的注意力分布进行了研究。实验刺激包括4个目标项目(如图,4个项目标有不同字母(每个字母代表不同颜色))和4个干扰项目。在索引阶段会呈现8个项目,同时提示被试哪些是目标项目。在追踪阶段8个项目随机运动(目标的颜色消失变得与干扰项目一样),其中4个目标的运动形式会破坏其构型(非拓扑变换)。如图,关键点穿过对角的边缘时拓扑结构被破坏。其中,图中C点为关键点、对角两点A和B为相邻点,D为非相邻点。探测刺激是一个小圆点,会在追踪阶段中出现在其中一个目标项目中。当探测刺激出现时,需要被试快速的按按键确定,接着在反应阶段会出现一个目标,被试需要判断该目标的颜色是否发生变化。该实验要做的是,当探测刺激出现在目标项目的拓扑结构被破坏时(关键点刚刚在对角边缘时),测试被试对不同点的成绩。实验结果显示,当构型被破坏时,探测刺激出现在关键点时的成绩要显著高于其他两种情况,表明构型破坏时对关键点施加的注意最多。
另一项研究也发现,在构型破坏时刻,相比其他点,关键点的点探测任务绩效更高;但在构型破坏前期,这种"关键点"上的优势就已经存在,且离构型破坏时刻越近时优势越强;在构型破坏后的较长一段时间内关键点上的点探测绩效仍显著高于其他目标点。这表明构型的变化确实影响了注意在目标间的分配。(赵雷,2014)
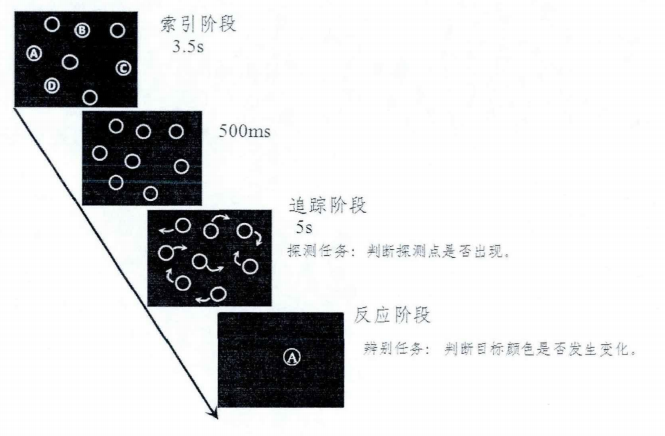
图17
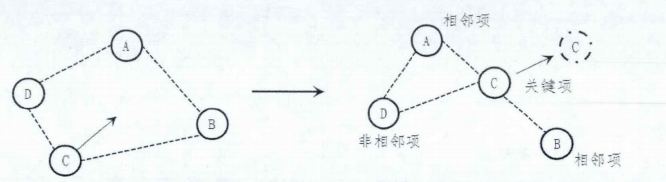
图18
4.意识水平
Chun等人(1998)的一项研究发现,在若干个客体中搜索一个特定目标时,如果这些客体组成的构型是重复出现过的,其绩效就会更高,而如果客体组成了一个未出现过的新构型,其绩效就低于前者。在这项研究中,研究者没有提示被试对重复出现的构型进行记忆,被试的任务只是寻找刺激目标,然而重复出现的构型显示出了对搜索任务的影响,这说明构型的信息在重复出现时得到了保持,并且这种保持并非有意识进行的。
五.存储
为了测试构型工作记忆的容量大小,黄羽商(2018)进行了实验。该实验与其在"编码"阶段的实验类似,不同的是在学习阶段可能会出现1、2和3个构型(每个构型包含4个不同颜色的圆,并分别位于不同象限。与呈现在同一位置相比,将不同构型呈现在不同象限是为了避免构型之间的相互干扰),如图。当构型数量大于1时,它们按照先后顺序出现,即展现完第一个学习构型后,展现第二个...。实验结果表明,学习阶段展示1个构型或2个构型时,被试成绩相当,而当展示3个构型时,被试的成绩会下降。这表明,视觉构型工作记忆的容量为2。图中显示了3个学习构型。