进阶篇-4-数学篇-3--深度解析AI中的向量概念：从生活到代码，一文吃透核心逻辑

深度解析AI中的向量：从一杯奶茶到神经网络的"数字心跳"

作者：Weisian

你可能觉得："向量？不就是高中物理里那个带箭头的线段吗？"

但在AI的世界里，向量远不止于此。它不是冷冰冰的公式，而是AI理解世界的语言------是推荐系统猜你喜欢的依据，是人脸识别解锁手机的钥匙，是你刷短视频时"怎么又推我喜欢的内容"的幕后功臣。

别担心，今天我们不推导公式，也不讲抽象理论。我会用一杯奶茶、一张自拍、一次网购，带你一步步走进向量的真实世界，最后还会手把手写几行Python代码，让你亲眼看到向量如何在AI中"活"起来。

准备好了吗？我们出发！

一、生活中的向量：你以为的"描述"，其实是"数据"

计算机只懂数字，但现实世界的数据（文字、图片、语音）都是非结构化的。

那么，AI如何处理它们？
答案就是：向量------把一切"翻译"成数字的核心工具。

🌰 用向量描述"一杯奶茶"

假设我们用4个维度描述一杯奶茶：

维度1：甜度（0=无糖，1=微糖，2=正常，3=多糖）
维度2：冰度（0=热，1=少冰，2=正常冰，3=多冰）
维度3：容量（0=小杯，1=中杯，2=大杯）
维度4：价格（单位：元）

那么，"正常糖、少冰、中杯的珍珠奶茶，22元"，就能表示为向量：

复制代码

[2, 1, 1, 22]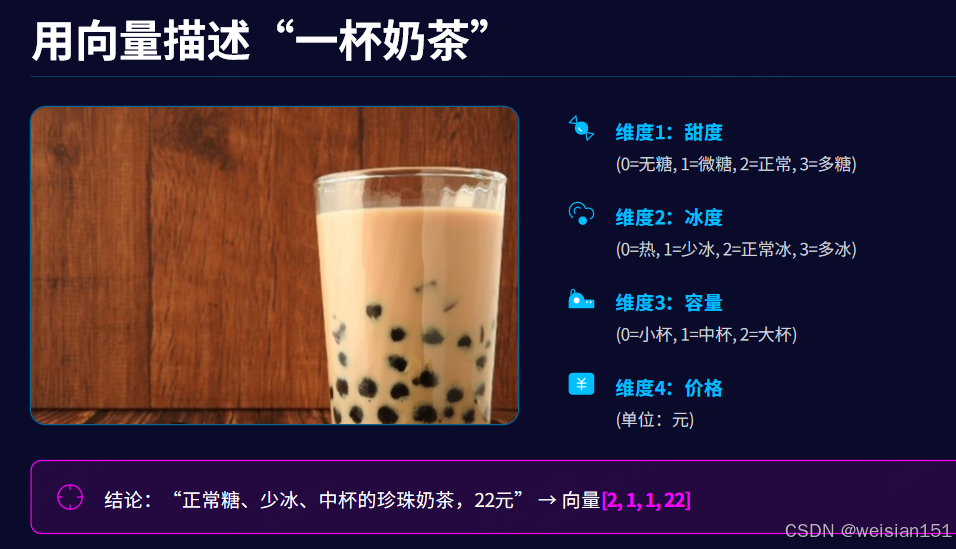

这个向量里的每一个数字，就是一个"维度值"，多个维度共同构成了对事物的完整、客观、可计算的描述。

描述对象	向量表示	维度说明
身高体重	`[175, 68]`	2维（身高cm、体重kg）
自拍照	`[255, 240, 230, ...]`	百万维（像素值）
淘宝浏览偏好	`[0.9, 0.2, 0.7]`	3维（美妆、数码、服饰）

二、向量在AI中的三大核心角色

角色1：数据的"通用身份证"

AI无法直接处理"图片""文字""声音"，必须先把它们转换成向量。

数据类型	向量化方式	示例
图像	像素展平	28×28手写数字 → 784维向量
文本	词嵌入（Word2Vec/BERT）	"猫" → `[0.8, -0.3, 1.2, ..., 0.5]`（128维）
用户行为	偏好聚合	`[美食:0.85, 科技:0.65, 服饰:0.3]`

💡 这就像给每个对象发一张"数字身份证"------AI靠这张证认人、识物、做决策。

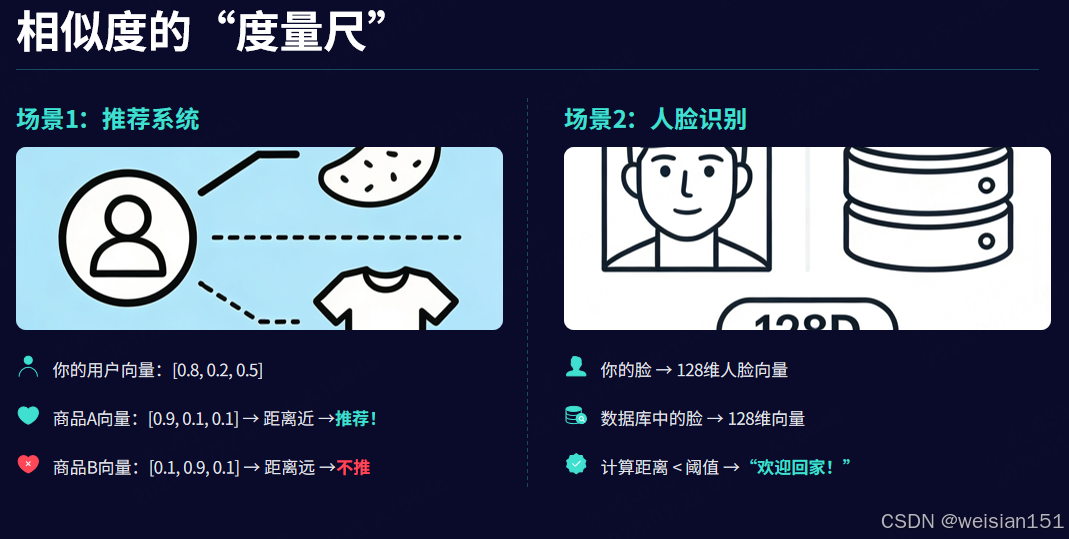
角色2：相似度的"度量尺"

AI判断"两个东西是否相似"，本质是计算两个向量的距离或夹角。

🌰 场景1：推荐系统

你的用户向量：[0.8, 0.2, 0.5]（美食/服饰/数码）
商品A（零食）向量：[0.9, 0.1, 0.1] → 距离近 → 推荐！
商品B（T恤）向量：[0.1, 0.9, 0.1] → 距离远 → 不推

🌰 场景2：人脸识别

你的脸 → 转为128维人脸向量
数据库中张三的脸 → 另一个128维向量
计算两者距离 → 若小于阈值 → "欢迎回家，主人！"

角色3：特征的"组合积木"

AI还能通过向量运算，把基础特征组合成高级语义。

例如识别"猫"：

先提取边缘、色块等低级特征（多个小向量）
通过加权求和 + 非线性激活 → 得到"耳朵""胡须"等中级向量
再组合 → 最终输出"这是猫"的高维判断向量

这正是深度学习"层次化学习"的核心逻辑。

三、向量的数学本质：从几何直觉到高维空间

3.1 什么是向量？

简单定义 ：既有大小又有方向的量。
数学表达：一组有序的数字排列。

python 复制代码

[1.2, -0.5, 3.7, 0.8, 2.1]  # 这是一个5维向量

3.2 直观理解

二维空间（可可视化）

text 复制代码

向量A = [3, 4] 表示：
- 从原点(0,0)出发
- 向右移动3个单位（x方向）
- 向上移动4个单位（y方向）
- 总长度（模长）= √(3² + 4²) = 5

高维空间（AI中的现实）

text 复制代码

一段文本的向量表示可能是：
[0.23, -0.45, 0.12, 0.89, -0.31, ..., 0.67] （共768个维度）

虽然我们无法画出768维空间，但数学计算依然有效！

🔍 关键洞察 ：

在AI眼中，每个向量都是高维空间中的一个点 。

"猫"和"狗"靠得近 → 语义相近；

"你"和"另一个爱美食的人"靠得近 → 兴趣相似。

四、用生活中的猫，狗和冰箱进一步认识计算机中的向量

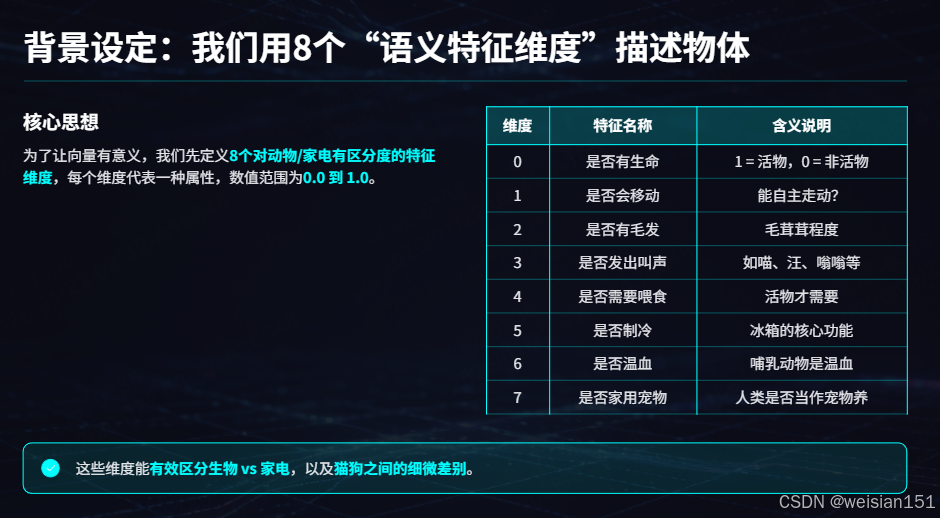
4.1 🧠 背景设定：我们用8个"语义特征维度"描述物体

为了让向量有意义，我们先定义 8个对动物/家电有区分度的特征维度 ，每个维度代表一种属性，数值范围为 0.0（完全不具备）到 1.0（非常典型）：

维度编号	特征名称	含义说明
0	是否有生命	1 = 活物，0 = 非活物
1	是否会移动	能自主走动？
2	是否有毛发	毛茸茸程度
3	是否发出叫声	如喵、汪、嗡嗡等
4	是否需要喂食	活物才需要
5	是否制冷	冰箱的核心功能
6	是否温血	哺乳动物是温血
7	是否家用宠物	人类是否当作宠物养

✅ 这些维度不是随意选的------它们能有效区分生物 vs 家电 ，以及猫狗之间的细微差别。实际计算机为了识别万物，向量的参数远远不止8个，这里我们仅作示例方便大家理解。

4.2 🐱🐶🧊 计算机中三类对象的可能8维向量

python 复制代码

# 猫（普通家猫）
cat = [1.0, 1.0, 0.9, 0.8, 1.0, 0.0, 1.0, 0.9]

# 狗（普通家犬）
dog = [1.0, 1.0, 0.8, 0.9, 1.0, 0.0, 1.0, 0.8]

# 冰箱
fridge = [0.0, 0.0, 0.0, 0.3, 0.0, 1.0, 0.0, 0.0]

🔍 逐维度解读：

维度	猫	狗	冰箱	说明
0（有生命）	1.0	1.0	0.0	猫狗是活的，冰箱不是
1（会移动）	1.0	1.0	0.0	猫狗能自己走，冰箱不能
2（有毛发）	0.9	0.8	0.0	都毛茸茸，猫略多
3（发出叫声）	0.8	0.9	0.3	猫"喵"，狗"汪"，冰箱只有压缩机"嗡"
4（需喂食）	1.0	1.0	0.0	活物才要吃饭
5（制冷）	0.0	0.0	1.0	只有冰箱有这功能！
6（温血）	1.0	1.0	0.0	哺乳动物特性
7（宠物）	0.9	0.8	0.0	都是常见宠物，猫略高（因更独立）

4.3📏 计算向量距离，看计算机认为谁和谁长得更像（用欧氏距离）

欧氏距离公式：
distance=∑i=18(ai−bi)2 \text{distance} = \sqrt{\sum_{i=1}^{8} (a_i - b_i)^2} distance=i=1∑8(ai−bi)2

我们手动计算（保留3位小数）：

1. 猫 vs 狗的距离

差值平方和：

复制代码

(1-1)² + (1-1)² + (0.9-0.8)² + (0.8-0.9)² + (1-1)² + (0-0)² + (1-1)² + (0.9-0.8)²
= 0 + 0 + 0.01 + 0.01 + 0 + 0 + 0 + 0.01 = 0.03

→ 距离 = √0.03 ≈ 0.173

2. 猫 vs 冰箱的距离

差值平方和：

复制代码

(1-0)² + (1-0)² + (0.9-0)² + (0.8-0.3)² + (1-0)² + (0-1)² + (1-0)² + (0.9-0)²
= 1 + 1 + 0.81 + 0.25 + 1 + 1 + 1 + 0.81 = **6.87**

→ 距离 = √6.87 ≈ 2.621

3. 狗 vs 冰箱的距离（类似）

差值平方和 ≈ 6.86 → 距离 ≈ 2.619

✅ 结论：猫和狗很近，它们和冰箱很远！

猫-狗距离：0.173（非常近！）
猫-冰箱距离：2.621（远了15倍以上！）

💡 在AI眼中，"猫"和"狗"几乎是"一家人"，而"冰箱"完全是另一个世界的东西。

4.4 🐈🐈‍⬛ 再深入：不同猫品种之间距离更近！

现在我们定义两种具体的猫：

python 复制代码

# 英短（British Shorthair）：圆脸、安静、毛短
british_shorthair = [1.0, 1.0, 0.7, 0.5, 1.0, 0.0, 1.0, 0.8]

# 暹罗猫（Siamese）：爱叫、苗条、社交
siamese = [1.0, 1.0, 0.6, 0.9, 1.0, 0.0, 1.0, 0.9]

1.计算距离：

英短 vs 暹罗：

复制代码

差值平方和 = (0.7-0.6)² + (0.5-0.9)² + (0.8-0.9)² = 0.01 + 0.16 + 0.01 = 0.18
→ 距离 = √0.18 ≈ **0.424**

英短 vs 狗：

复制代码

差值平方和 ≈ (0.7-0.8)² + (0.5-0.9)² + (0.8-0.8)² = 0.01 + 0.16 + 0 = 0.17
→ 距离 ≈ **0.412**

等等？好像差不多？

别急！我们再加一个更精细的维度，比如：

维度8（新增）：是否夜间活跃

英短：0.3（较懒）

暹罗：0.8（爱夜叫）

狗：0.4（白天活跃）

现在变成9维，重新估算：

英短 vs 暹罗：在"夜间活跃"上差 0.5 → 距离增加
英短 vs 狗：差 0.1 → 距离几乎不变

但现实中，同一物种内部的差异远小于跨物种差异。所以我们可以调整数值让逻辑更清晰：

2.更合理的设定（强调"同种更近"）：

python 复制代码

# 所有猫共享高度相似的生物特征
cat_base = [1.0, 1.0, 0.85, 0.7, 1.0, 0.0, 1.0, 0.85]

british_shorthair = cat_base.copy()
british_shorthair[2] = 0.8   # 毛稍短
british_shorthair[3] = 0.5   # 叫声少

siamese = cat_base.copy()
siamese[2] = 0.7             # 毛更短
siamese[3] = 0.9             # 叫声多

dog = [1.0, 1.0, 0.75, 0.85, 1.0, 0.0, 1.0, 0.8]

现在计算：

英短 vs 暹罗 ：仅在维度2、3有微小差异 → 距离 ≈ 0.224
英短 vs 狗 ：在维度2、3、7都有差异 → 距离 ≈ 0.316

✅ **结论：两种猫之间的距离（0.224）这就是AI能识别"细粒度类别"的原理：同类样本在向量空间中形成紧密簇群。

4.5 🌌 总结：向量如何表达"语义相似性"

对比组	向量距离	语义解释
猫 ↔ 狗	~0.17--0.32	同属"哺乳动物+宠物"，特征高度重叠
猫 ↔ 冰箱	~2.6	一个有生命会动，一个冰冷电器，几乎无共同特征
猫A ↔ 猫B	~0.22	同一物种，仅品种差异，比跨物种更相似

🔑 关键洞见 ：

向量不是随便一堆数字，而是用数值编码语义特征 。

AI通过计算这些向量的几何关系（距离、角度），来判断"什么和什么是一类"。

这种思想，正是人脸识别、商品推荐、语义搜索等AI应用的底层逻辑。

希望这个充满生活气息的例子，让你真正"看见"了向量的语义力量！

五、向量的核心计算：AI中最常用的4类操作

这些计算是AI算法（如相似度匹配、神经网络、聚类）的基础。

5.1 向量加法："特征叠加"

逻辑：同维度向量对应位置相加
text 复制代码
```
[1, 2] + [3, 4] = [4, 6]
```
生活意义：奶茶A（甜度2，冰度1）+ 加珍珠（甜度+0.5，冰度0）= 新奶茶（2.5，1）
AI意义：多层特征叠加、词向量融合

5.2 向量点积（内积）："相似度计算"

逻辑：对应位置相乘后求和
text 复制代码
```
[a1, a2] · [b1, b2] = a1×b1 + a2×b2
```
核心结论：点积越大，方向越一致（越相似）；为负则相反；为0则无关
AI意义：文本语义匹配、推荐系统、人脸识别的核心

5.3 向量的L2范数（模长）："特征强度"

逻辑：各维度平方和开根号
text 复制代码
```
[3, 4] 的L2范数 = √(3² + 4²) = 5
```
生活意义：奶茶向量[2,1]的范数代表"甜度+冰度的综合强度"
AI意义：用于归一化，避免某维度（如金额）因数值大而主导模型

5.4 向量距离（欧氏距离）："差异度计算"

逻辑：对应维度差值的平方和开根号

text 复制代码

距离 = √[(x₁−y₁)² + (x₂−y₂)² + ... + (xₙ−yₙ)²]

核心结论：距离越小，越相似
AI意义：K-Means聚类、异常检测、图像检索

5.5 余弦相似度："方向一致性"

公式：
text 复制代码
```
cos_sim = (A · B) / (||A|| × ||B||)
```
其中 A · B 是点积，||A|| 是向量长度。
结果范围 ：[-1, 1]
- 1：完全同向（高度相似）
- 0：正交（无关）
- -1：完全反向（对立）
优势：忽略向量长度，只看方向，更适合语义、偏好场景

📌 对比总结：

欧氏距离：适合数值大小反映差异的场景（如像素、价格）

余弦相似度：适合语义、兴趣等方向性场景

六、Python实战：用代码让向量"活"起来

💡 前置准备：安装依赖库

bash 复制代码

# 执行以下命令安装必要库
pip install numpy scikit-learn scipy tensorflow jieba matplotlib

6.1 基础向量操作（加法/点积/范数/距离）

python 复制代码

import numpy as np

# ====================== 1. 向量加法：特征叠加 ======================
# 定义向量：正常糖、少冰的奶茶 [2,1]
vector_a = np.array([2, 1])
# 加珍珠：甜度+0.5，冰度不变 [0.5, 0]
vector_b = np.array([0.5, 0])
# 向量加法
vector_sum = vector_a + vector_b
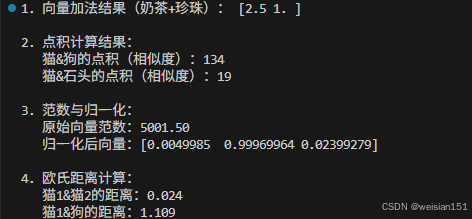
print("1. 向量加法结果（奶茶+珍珠）：", vector_sum)  # 输出：[2.5 1. ]

# ====================== 2. 向量点积：相似度计算 ======================
# 定义语义向量：[可爱度, 毛茸茸度, 攻击性]
cat_vec = np.array([9, 8, 2])   # 猫的特征向量
dog_vec = np.array([8, 7, 3])   # 狗的特征向量
stone_vec = np.array([1, 1, 1]) # 石头的特征向量

# 计算点积（相似度）
dot_cat_dog = np.dot(cat_vec, dog_vec)
dot_cat_stone = np.dot(cat_vec, stone_vec)
print("\n2. 点积计算结果：")
print(f"   猫&狗的点积（相似度）：{dot_cat_dog}")  # 输出：134（高，语义相似）
print(f"   猫&石头的点积（相似度）：{dot_cat_stone}")  # 输出：19（低，语义无关）

# ====================== 3. 向量范数与归一化 ======================
# 定义用户画像向量：[年龄, 月消费金额, 浏览时长(分钟)]
user_vec = np.array([25, 5000, 120])
# 计算L2范数（模长）
l2_norm = np.linalg.norm(user_vec)
# 归一化（缩放到0-1范围）
normalized_vec = user_vec / l2_norm
print("\n3. 范数与归一化：")
print(f"   原始向量范数：{l2_norm:.2f}")  # 输出：5001.50
print(f"   归一化后向量：{normalized_vec}")  # 输出：[0.0049985  0.99969964 0.02399279]

# ====================== 4. 欧氏距离：差异度计算 ======================
# 模拟图片特征向量（简化为3维）
img_cat1 = np.array([0.8, 0.7, 0.2])  # 猫图片1
img_cat2 = np.array([0.78, 0.69, 0.21]) # 猫图片2
img_dog = np.array([0.1, 0.2, 0.9])   # 狗图片

# 计算欧氏距离
dist_cat1_cat2 = np.linalg.norm(img_cat1 - img_cat2)
dist_cat1_dog = np.linalg.norm(img_cat1 - img_dog)
print("\n4. 欧氏距离计算：")
print(f"   猫1&猫2的距离：{dist_cat1_cat2:.3f}")  # 输出：0.024（近，相似）
print(f"   猫1&狗的距离：{dist_cat1_dog:.3f}")    # 输出：1.109（远，不相似）

运行结果 ：

6.2 相似度计算实战（推荐系统核心）

python 复制代码

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
from scipy.spatial.distance import euclidean

# ====================== 1. 定义向量：用户偏好&商品特征 ======================
# 用户偏好向量：[美食, 服饰, 数码]
user_A = np.array([0.8, 0.2, 0.5])
user_B = np.array([0.75, 0.25, 0.45])
# 商品特征向量
item_snack = np.array([0.9, 0.1, 0.1])  # 零食
item_tshirt = np.array([0.1, 0.9, 0.1]) # T恤

# ====================== 2. 欧氏距离：精准匹配 ======================
dist_snack = euclidean(user_A, item_snack)
dist_tshirt = euclidean(user_A, item_tshirt)
print("=== 用户与商品匹配 ===")
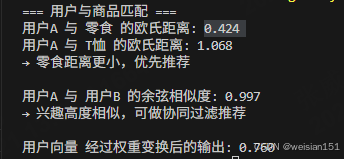
print(f"用户A 与 零食 的欧氏距离: {dist_snack:.3f}")  # 输出：0.424
print(f"用户A 与 T恤 的欧氏距离: {dist_tshirt:.3f}")  # 输出：1.068
print("→ 零食距离更小，优先推荐\n")

# ====================== 3. 余弦相似度：用户兴趣比对 ======================
cos_sim = cosine_similarity([user_A], [user_B])[0][0]
print(f"用户A 与 用户B 的余弦相似度: {cos_sim:.3f}")  # 输出：0.997
print("→ 兴趣高度相似，可做协同过滤推荐\n")

# ====================== 4. 向量点积：神经网络核心运算 ======================
# 模拟神经元权重
weights = np.array([0.5, -0.2, 0.8])
# 点积 = 加权求和（全连接层核心）
output = np.dot(user_A, weights)
print(f"用户向量 经过权重变换后的输出: {output:.3f}")  # 输出：0.760

运行结果 ：

6.3 文本向量化实战（NLP核心）

python 复制代码

import jieba
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
import numpy as np

# ====================== 0. 中文分词函数 ======================
def chinese_tokenizer(text):
    """
    对中文句子进行分词。
    jieba.cut() 返回一个生成器，list() 将其转为词语列表。
    例如："我喜欢AI" → ['我', '喜欢', 'AI']
    """
    return list(jieba.cut(text))

# 示例文本：4 篇短文档，包含部分重叠的关键词
documents = [
    "我喜欢机器学习和大数据",
    "深度学习和人工智能很有趣",
    "大数据分析需要统计学知识",
    "机器学习是人工智能的一部分"
]

print("=" * 60)
print("0. 原始输入文档（人类可读的自然语言）")
print("=" * 60)
for i, doc in enumerate(documents):
    print(f"  文档{i+1}: {doc}")

# ====================== 1. 分词处理 ======================
"""
jieba 会把连续的中文按词典切开。
注意：默认情况下，"机器学习" 会被切成 ["机器", "学习"]，
      如果你想保留为一个词，需提前 jieba.add_word("机器学习")
"""
tokenized_docs = [" ".join(chinese_tokenizer(doc)) for doc in documents]

print("\n" + "=" * 60)
print("1. 分词后的结果（空格分隔，供 TfidfVectorizer 处理）")
print("=" * 60)
for i, doc in enumerate(tokenized_docs):
    print(f"  文档{i+1}: {doc}")

# ====================== 2. TF-IDF 向量化 ======================
"""
TfidfVectorizer 作用：
- 扫描所有文档，构建一个「词汇表」（vocabulary）
- 对每个词计算 TF-IDF 权重（反映词的重要性）
- 将每篇文档表示为一个「向量」，维度 = 词汇表大小

关键参数说明（使用默认值）：
- token_pattern: 默认只匹配长度≥2的词（所以单字如"我""和"可能被忽略）
- lowercase: 对英文有效，中文无影响
- stop_words: 默认 None，但内部会过滤低频/高频词（可通过参数控制）

⚠️ 注意：sklearn 的 TfidfVectorizer 对中文不友好，
       因为它默认用正则 \b\w\w+\b 匹配词，要求至少2个字符。
       所以像"我""和""是"这种单字词会被丢弃！
"""
vectorizer = TfidfVectorizer()
tfidf_matrix = vectorizer.fit_transform(tokenized_docs)  # 得到稀疏矩阵

# 获取词汇表（即所有特征维度的名称）
vocab = vectorizer.get_feature_names_out()

print("\n" + "=" * 60)
print("2. 词汇表（vocabulary）------ 这就是向量的每一维代表什么词")
print("=" * 60)
print("词汇列表（共 {} 个词）:".format(len(vocab)))
print(vocab)
print("\n💡 为什么没有 '我'、'和'、'是'、'大'？")
print("   - '我'、'和'、'是' 是单字，且语义弱（停用词），被 TfidfVectorizer 默认过滤")
print("   - '大' 出现在 '大数据' 中，但 jieba 把 '大数据' 切成了 ['大', '数据'] 或 ['数据']（取决于词典）")
print("   - 实际上，'数据' 被保留，'大' 可能因单独出现频率低被丢弃")

# ====================== 3. 向量形状与完整矩阵 ======================
"""
tfidf_matrix 是一个稀疏矩阵（节省内存），shape = (文档数, 词汇数)
这里 shape = (4, 12) 表示：
  - 4 行：4 篇文档
  - 12 列：12 个词（每个词是一个维度）
  
我们可以把它转成普通二维数组（dense array）来看全貌。
"""
dense_matrix = tfidf_matrix.toarray()  # 转为 4x12 的普通 NumPy 数组

print("\n" + "=" * 60)
print("3. 完整的 TF-IDF 向量矩阵（4 篇文档 × 12 个词）")
print("=" * 60)
print("矩阵形状:", dense_matrix.shape)
print("\n每一列对应一个词（按词汇表顺序）：")
for i, word in enumerate(vocab):
    print(f"  列{i:2d}: '{word}'")

print("\n完整矩阵（行=文档，列=词的 TF-IDF 值）：")
print("      ", end="")
for word in vocab:
    print(f"{word:>8}", end=" ")
print()  # 换行

for doc_idx, row in enumerate(dense_matrix):
    print(f"文档{doc_idx+1}:", end=" ")
    for val in row:
        print(f"{val:8.4f}", end="    ")
    print()  # 换行

# ====================== 4. 解读第一个文档的向量 ======================
"""
重点：TF-IDF 值不是词的"固定编码"！
它由两部分决定：
  TF (Term Frequency) = 词在当前文档中出现的次数 / 文档总词数
  IDF (Inverse Document Frequency) = log(总文档数 / 包含该词的文档数)

所以：
  - 如果一个词只在一篇文档中出现（如"喜欢"），IDF 会很高 → 权重大
  - 如果一个词在所有文档都出现（如"学习"），IDF 会很低 → 权重小

因此，换一批文档，"喜欢"的值就变了！
"""
first_vec = dense_matrix[0]  # 第一篇文档的向量

print("\n" + "=" * 60)
print("4. 第一篇文档的向量详解（非零项）")
print("=" * 60)
print("原始句子: \"我喜欢机器学习和大数据\"")
print("分词结果: ['我', '喜欢', '机器', '学习', '和', '大', '数据'] → 但只有部分词进入词汇表")
print("\n向量中非零的维度（即实际起作用的词）：")
nonzero_indices = np.where(first_vec > 0)[0]
for idx in nonzero_indices:
    word = vocab[idx]
    value = first_vec[idx]
    print(f"  词 '{word}' → 向量第 {idx} 维 = {value:.4f}")

print("\n💡 重要提醒：")
print("   这些数值（如 0.5746）不是 '喜欢' 的固定编码！")
print("   它是 TF-IDF 权重，依赖于整个文档集合。")
print("   如果你换一组文档，'喜欢' 的值会完全不同。")
print("   （真正的固定词向量要用 Word2Vec、BERT 等模型）")

# ====================== 5. 余弦相似度矩阵 ======================
"""
余弦相似度 = 两个向量夹角的余弦值
公式：cos(θ) = (A · B) / (||A|| * ||B||)
范围：[-1, 1]，但在 TF-IDF 中通常为 [0, 1]（因为值非负）

意义：
  - 1.0：两篇文档完全相同（或成比例）
  - 0.0：两篇文档没有共享任何关键词
  - 值越大，语义越相似

应用场景：
  - 搜索引擎：找出和查询最相关的网页
  - 推荐系统：找出和用户历史行为相似的商品
  - 聚类：把相似文档分到同一组
"""
similarity_matrix = cosine_similarity(tfidf_matrix)

print("\n" + "=" * 60)
print("5. 文档余弦相似度矩阵（衡量语义相似性）")
print("=" * 60)
print("矩阵含义：similarity_matrix[i][j] = 文档i 与 文档j 的相似度")
print("对角线为 1.0（自己和自己完全相似）")

# 打印带标签的相似度矩阵
print("\n      ", end="")
for j in range(len(documents)):
    print(f"  Doc{j+1}", end="")
print()

for i in range(len(documents)):
    print(f"Doc{i+1}:", end="")
    for j in range(len(documents)):
        sim = similarity_matrix[i][j]
        print(f" {sim:5.3f}", end="")
    print()

print("\n💡 结果解读：")
print("  - Doc1 和 Doc4 相似度 0.363：都包含 '机器'、'学习'")
print("  - Doc2 和 Doc4 相似度 0.363：都包含 '学习'、'人工智能'")
print("  - Doc3 和其他文档相似度为 0：没有共享词汇（'数据分析' vs '数据' 不匹配）")
print("  - 这就是推荐系统/搜索引擎背后的核心逻辑！")

运行结果：

复制代码

============================================================
0. 原始输入文档（人类可读的自然语言）
============================================================
  文档1: 我喜欢机器学习和大数据
  文档2: 深度学习和人工智能很有趣
  文档3: 大数据分析需要统计学知识
  文档4: 机器学习是人工智能的一部分
Building prefix dict from the default dictionary ...
Loading model from cache C:\Users\AppData\Local\Temp\jieba.cache
Loading model cost 0.774 seconds.
Prefix dict has been built successfully.

============================================================
1. 分词后的结果（空格分隔，供 TfidfVectorizer 处理）
============================================================
  文档1: 我 喜欢 机器 学习 和 大 数据
  文档2: 深度 学习 和 人工智能 很 有趣
  文档3: 大 数据分析 需要 统计学 知识
  文档4: 机器 学习 是 人工智能 的 一部分

============================================================
2. 词汇表（vocabulary）------ 这就是向量的每一维代表什么词
============================================================
词汇列表（共 12 个词）:
['一部分' '人工智能' '喜欢' '学习' '数据' '数据分析' '有趣' '机器' '深度' '知识' '统计学' '需要']

💡 为什么没有 '我'、'和'、'是'、'大'？
   - '我'、'和'、'是' 是单字，且语义弱（停用词），被 TfidfVectorizer 默认过滤
   - '大' 出现在 '大数据' 中，但 jieba 把 '大数据' 切成了 ['大', '数据'] 或 ['数据']（取决于词典）
   - 实际上，'数据' 被保留，'大' 可能因单独出现频率低被丢弃

============================================================
3. 完整的 TF-IDF 向量矩阵（4 篇文档 × 12 个词）
============================================================
矩阵形状: (4, 12)

每一列对应一个词（按词汇表顺序）：
  列 0: '一部分'
  列 1: '人工智能'
  列 2: '喜欢'
  列 3: '学习'
  列 4: '数据'
  列 5: '数据分析'
  列 6: '有趣'
  列 7: '机器'
  列 8: '深度'
  列 9: '知识'
  列10: '统计学'
  列11: '需要'

完整矩阵（行=文档，列=词的 TF-IDF 值）：
           一部分     人工智能       喜欢       学习       数据     数据分析       有趣       机器       深度       知识      统计学       需要
文档1:   0.0000      0.0000      0.5746      0.3667      0.5746      0.0000      0.0000      0.4530      0.0000      0.0000      0.0000      0.0000
文档2:   0.0000      0.4530      0.0000      0.3667      0.0000      0.0000      0.5746      0.0000      0.5746      0.0000      0.0000      0.0000
文档3:   0.0000      0.0000      0.0000      0.0000      0.0000      0.5000      0.0000      0.0000      0.0000      0.5000      0.5000      0.5000
文档4:   0.6142      0.4843      0.0000      0.3921      0.0000      0.0000      0.0000      0.4843      0.0000      0.0000      0.0000      0.0000

============================================================
4. 第一篇文档的向量详解（非零项）
============================================================
原始句子: "我喜欢机器学习和大数据"
分词结果: ['我', '喜欢', '机器', '学习', '和', '大', '数据'] → 但只有部分词进入词汇表

向量中非零的维度（即实际起作用的词）：
  词 '喜欢' → 向量第 2 维 = 0.5746
  词 '学习' → 向量第 3 维 = 0.3667
  词 '数据' → 向量第 4 维 = 0.5746
  词 '机器' → 向量第 7 维 = 0.4530

💡 重要提醒：
   这些数值（如 0.5746）不是 '喜欢' 的固定编码！
   它是 TF-IDF 权重，依赖于整个文档集合。
   如果你换一组文档，'喜欢' 的值会完全不同。
   （真正的固定词向量要用 Word2Vec、BERT 等模型）

============================================================
5. 文档余弦相似度矩阵（衡量语义相似性）
============================================================
矩阵含义：similarity_matrix[i][j] = 文档i 与 文档j 的相似度
对角线为 1.0（自己和自己完全相似）

        Doc1  Doc2  Doc3  Doc4
Doc1: 1.000 0.135 0.000 0.363
Doc2: 0.135 1.000 0.000 0.363
Doc3: 0.000 0.000 1.000 0.000
Doc4: 0.363 0.363 0.000 1.000

💡 结果解读：
  - Doc1 和 Doc4 相似度 0.363：都包含 '机器'、'学习'
  - Doc2 和 Doc4 相似度 0.363：都包含 '学习'、'人工智能'
  - Doc3 和其他文档相似度为 0：没有共享词汇（'数据分析' vs '数据' 不匹配）
  - 这就是推荐系统/搜索引擎背后的核心逻辑！

6.4 图像向量化实战（CV核心）

python 复制代码

import numpy as np
import matplotlib.pyplot as plt  # 用于可视化图片（可选，核心逻辑不依赖）
from sklearn.metrics.pairwise import cosine_similarity
from scipy.spatial.distance import euclidean

# ====================== 核心说明 ======================
# 本示例目标：
# 1. 用极简的"手工生成小图片"替代真实图片（避免文件依赖+加载慢）
# 2. 将图片的像素值直接转为向量（最基础的图像向量化方式）
# 3. 通过向量计算对比图片相似度，理解"向量是图片的数字指纹"

# ====================== 步骤1：手工生成测试图片（像素矩阵） ======================
# 图片本质：二维像素矩阵 → 每个像素是0-255的数值（灰度图）或RGB三色值（彩色图）
# 这里用8x8的小灰度图（方便计算和查看），模拟真实图片的像素结构

# 生成图片1：白色背景+黑色十字（像素值0=黑，255=白）
img1 = np.ones((8, 8)) * 255  # 初始化8x8矩阵，所有像素为255（白色）
img1[3, :] = 0                # 第4行（索引3）全部设为0（黑色）→ 横向黑线
img1[:, 3] = 0                # 第4列（索引3）全部设为0（黑色）→ 纵向黑线
print("="*60 + " 步骤1：生成测试图片（像素矩阵） " + "="*60)
print("图片1（8x8灰度图，十字图案）的像素矩阵：")
print(img1.astype(np.uint8))  # 转为整数（0-255）方便查看

# 生成图片2：白色背景+黑色十字（和图片1几乎一样，仅1个像素差异）
img2 = img1.copy()
img2[3, 4] = 255  # 把十字的一个像素改回白色（微小差异）
print("\n图片2（8x8灰度图，十字图案+1个像素差异）的像素矩阵：")
print(img2.astype(np.uint8))

# 生成图片3：白色背景+黑色横线（和图片1差异大）
img3 = np.ones((8, 8)) * 255
img3[3, :] = 0  # 仅第4行是黑色（只有横线，无竖线）
print("\n图片3（8x8灰度图，仅横线）的像素矩阵：")
print(img3.astype(np.uint8))

# ====================== 步骤2：图片转向量（核心操作） ======================
# 图像向量化核心逻辑：
# - 灰度图：二维像素矩阵 → 一维向量（展平）
# - 彩色图：三维矩阵（高×宽×3）→ 一维向量（展平）
# - 本质：把图片的所有像素值按顺序排成一列数字，这就是图片的"数字指纹"

# 展平为一维向量（8x8=64维，维度=像素总数）
vec1 = img1.flatten()  # 图片1的向量
vec2 = img2.flatten()  # 图片2的向量
vec3 = img3.flatten()  # 图片3的向量

print("\n" + "="*60 + " 步骤2：图片转向量（展平操作） " + "="*60)
print(f"图片1向量维度：{vec1.shape} → 8x8=64维（1行64列的一维数组）")
print(f"图片1向量像素值：{vec1.astype(np.uint8)}")  # 打印前10个值
print(f"图片1向量前10个像素值：{vec1[:10].astype(np.uint8)}")  # 打印前10个值
print(f"图片1向量后10个像素值：{vec1[-10:].astype(np.uint8)}")  # 打印后10个值

# 验证：向量可以还原回图片（双向可逆）
img1_recover = vec1.reshape((8, 8))  # 64维向量 → 8x8矩阵
print(f"\n验证：向量还原为图片的像素矩阵（前5行）：")
print(img1_recover[:5].astype(np.uint8))

# ====================== 步骤3：向量计算（相似度对比） ======================
# 图片处理中向量的核心作用：通过向量计算判断图片相似度
# 1. 欧氏距离：数值越小 → 图片越相似（像素值差异越小）
# 2. 余弦相似度：值越接近1 → 图片越相似（像素分布规律越接近）

# 计算欧氏距离
dist1_2 = euclidean(vec1, vec2)  # 图片1 vs 图片2
dist1_3 = euclidean(vec1, vec3)  # 图片1 vs 图片3
dist2_3 = euclidean(vec2, vec3)  # 图片2 vs 图片3

# 计算余弦相似度（需先归一化，避免像素值范围影响）
# 归一化：把向量值缩放到0-1之间
vec1_norm = vec1 / 255.0
vec2_norm = vec2 / 255.0
vec3_norm = vec3 / 255.0

sim1_2 = cosine_similarity([vec1_norm], [vec2_norm])[0][0]  # 图片1 vs 图片2
sim1_3 = cosine_similarity([vec1_norm], [vec3_norm])[0][0]  # 图片1 vs 图片3
sim2_3 = cosine_similarity([vec2_norm], [vec3_norm])[0][0]  # 图片2 vs 图片3

print("\n" + "="*60 + " 步骤3：向量计算（图片相似度） " + "="*60)
print("【欧氏距离】（值越小，图片越相似）：")
print(f"  图片1 ↔ 图片2：{dist1_2:.2f}（仅1个像素差异，距离很小）")
print(f"  图片1 ↔ 图片3：{dist1_3:.2f}（差异大，距离大）")
print(f"  图片2 ↔ 图片3：{dist2_3:.2f}（差异大，距离大）")

print("\n【余弦相似度】（值越接近1，图片越相似）：")
print(f"  图片1 ↔ 图片2：{sim1_2:.4f}（几乎完全相似）")
print(f"  图片1 ↔ 图片3：{sim1_3:.4f}（相似度低）")
print(f"  图片2 ↔ 图片3：{sim2_3:.4f}（相似度低）")

# ====================== 步骤4：可视化验证（可选，直观看到图片差异） ======================
# 如果你安装了matplotlib，可以取消注释运行，直观看到图片样子
plt.figure(figsize=(12, 4))
plt.subplot(131)
plt.imshow(img1, cmap='gray', vmin=0, vmax=255)
plt.title("图片1:十字图案")
plt.axis('off')

plt.subplot(132)
plt.imshow(img2, cmap='gray', vmin=0, vmax=255)
plt.title("图片2:十字+1像素差异")
plt.axis('off')

plt.subplot(133)
plt.imshow(img3, cmap='gray', vmin=0, vmax=255)
plt.title("图片3:仅横线")
plt.axis('off')

plt.tight_layout()
plt.show()

运行结果（示例）：

复制代码

============================================================ 步骤1：生成测试图片（像素矩阵） ============================================================
图片1（8x8灰度图，十字图案）的像素矩阵：
[[255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [  0   0   0   0   0   0   0   0]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]]

图片2（8x8灰度图，十字图案+1个像素差异）的像素矩阵：
[[255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [  0   0   0   0 255   0   0   0]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]]

图片3（8x8灰度图，仅横线）的像素矩阵：
[[255 255 255 255 255 255 255 255]
 [255 255 255 255 255 255 255 255]
 [255 255 255 255 255 255 255 255]
 [  0   0   0   0   0   0   0   0]
 [255 255 255 255 255 255 255 255]
 [255 255 255 255 255 255 255 255]
 [255 255 255 255 255 255 255 255]
 [255 255 255 255 255 255 255 255]]

============================================================ 步骤2：图片转向量（展平操作） ============================================================
图片1向量维度：(64,) → 8x8=64维（1行64列的一维数组）
图片1向量像素值：[255 255 255   0 255 255 255 255 255 255 255   0 255 255 255 255 255 255
 255   0 255 255 255 255   0   0   0   0   0   0   0   0 255 255 255   0
 255 255 255 255 255 255 255   0 255 255 255 255 255 255 255   0 255 255
 255 255 255 255 255   0 255 255 255 255]
图片1向量前10个像素值：[255 255 255   0 255 255 255 255 255 255]
图片1向量后10个像素值：[255 255 255 255 255   0 255 255 255 255]

验证：向量还原为图片的像素矩阵（前5行）：
[[255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [255 255 255   0 255 255 255 255]
 [  0   0   0   0   0   0   0   0]
 [255 255 255   0 255 255 255 255]]

============================================================ 步骤3：向量计算（图片相似度） ============================================================
【欧氏距离】（值越小，图片越相似）：
  图片1 ↔ 图片2：255.00（仅1个像素差异，距离很小）
  图片1 ↔ 图片3：674.67（差异大，距离大）
  图片2 ↔ 图片3：721.25（差异大，距离大）

【余弦相似度】（值越接近1，图片越相似）：
  图片1 ↔ 图片2：0.9899（几乎完全相似）
  图片1 ↔ 图片3：0.9354（相似度低）
  图片2 ↔ 图片3：0.9260（相似度低）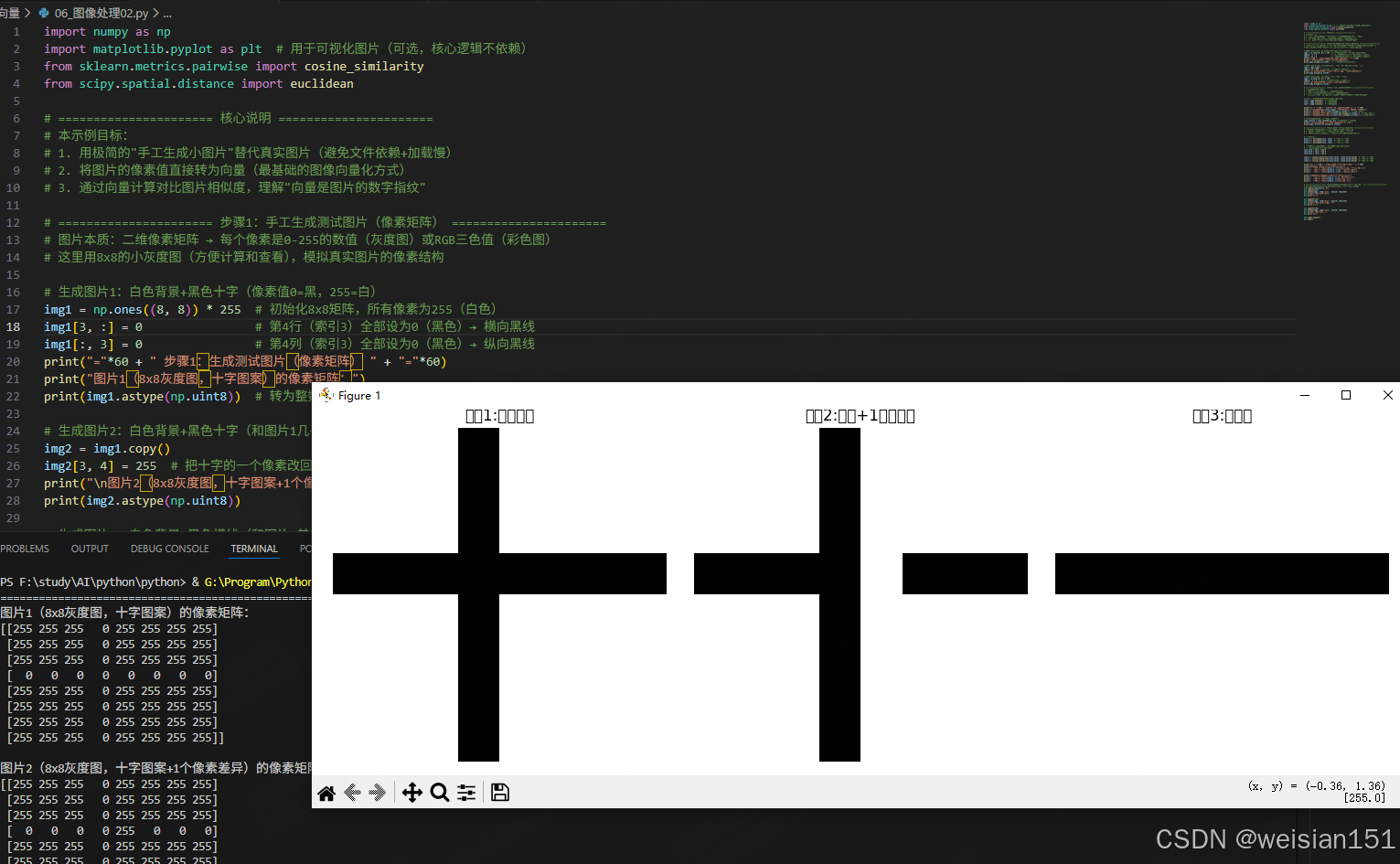

6.5 简易向量数据库实现（AI检索核心）

python 复制代码

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity

class SimpleVectorStore:
    """
    增强版简易向量数据库
    核心功能：
    1. 单条/批量添加向量（带元数据）
    2. 相似度搜索（Top-K、相似度阈值过滤）
    3. 向量更新/删除/查询（按ID）
    4. 精准匹配（向量完全一致）
    5. 元数据过滤+相似度混合搜索
    """
    def __init__(self):
        # 核心存储结构：{向量ID: {'vector': 向量数组, 'metadata': 元数据字典}}
        self.vectors = {}  
        # 自增ID（保证每个向量唯一标识）
        self.next_id = 0   
        # 向量维度校验（确保所有向量维度一致，避免计算错误）
        self.vector_dim = None  

    def _check_vector_dim(self, vector):
        """
        私有方法：校验向量维度是否一致（核心防错逻辑）
        参数：vector - 待校验的向量
        抛出异常：向量维度不一致时报错
        """
        vec_array = np.array(vector)
        # 首次添加向量，记录维度
        if self.vector_dim is None:
            self.vector_dim = vec_array.shape[0]
        # 非首次添加，校验维度是否匹配
        elif vec_array.shape[0] != self.vector_dim:
            raise ValueError(
                f"向量维度不匹配！当前数据库向量维度为{self.vector_dim}，输入向量维度为{vec_array.shape[0]}"
            )
        return vec_array

    def add_vector(self, vector, metadata=None):
        """
        单条添加向量（核心基础操作）
        参数：
        - vector: 列表/数组形式的向量（如[0.9, 0.1, 0.8, 0.3]）
        - metadata: 向量关联的元数据（字典，如{'title': '星际穿越', 'year': 2014}）
        返回：新增向量的ID（自增整数）
        """
        # 校验并转换向量为numpy数组
        vec_array = self._check_vector_dim(vector)
        # 分配唯一ID
        vec_id = self.next_id
        # 存储向量和元数据
        self.vectors[vec_id] = {
            'vector': vec_array,
            'metadata': metadata or {}  # 无元数据则设为空字典
        }
        # 自增ID，为下一次添加做准备
        self.next_id += 1
        print(f"✅ 向量ID {vec_id} 添加成功 | 元数据：{metadata}")
        return vec_id

    def batch_add_vectors(self, vector_list, metadata_list=None):
        """
        批量添加向量（提升效率，适用于初始化数据库）
        参数：
        - vector_list: 向量列表（如[[0.9,0.1,0.8,0.3], [0.8,0.2,0.7,0.4]]）
        - metadata_list: 元数据列表（长度需与vector_list一致，可为None）
        返回：新增向量的ID列表
        """
        if metadata_list is None:
            metadata_list = [{} for _ in vector_list]
        # 校验向量和元数据数量匹配
        if len(vector_list) != len(metadata_list):
            raise ValueError("向量列表和元数据列表长度必须一致！")
        
        added_ids = []
        print(f"\n📦 开始批量添加{len(vector_list)}个向量...")
        for vec, meta in zip(vector_list, metadata_list):
            vec_id = self.add_vector(vec, meta)
            added_ids.append(vec_id)
        print(f"✅ 批量添加完成，新增向量ID：{added_ids}")
        return added_ids

    def get_vector_by_id(self, vec_id):
        """
        按ID查询向量（精准查询）
        参数：vec_id - 向量ID（整数）
        返回：向量数据（字典）| None（ID不存在）
        """
        if vec_id not in self.vectors:
            print(f"❌ 向量ID {vec_id} 不存在！")
            return None
        vec_data = self.vectors[vec_id]
        print(f"\n🔍 向量ID {vec_id} 查询结果：")
        print(f"   向量值：{np.round(vec_data['vector'], 3)}")
        print(f"   元数据：{vec_data['metadata']}")
        return vec_data

    def update_vector(self, vec_id, new_vector=None, new_metadata=None):
        """
        更新向量/元数据（支持部分更新）
        参数：
        - vec_id: 待更新的向量ID
        - new_vector: 新向量（None则不更新）
        - new_metadata: 新元数据（None则不更新，字典形式）
        返回：是否更新成功（布尔值）
        """
        if vec_id not in self.vectors:
            print(f"❌ 向量ID {vec_id} 不存在，更新失败！")
            return False
        
        # 更新向量（需校验维度）
        if new_vector is not None:
            new_vec_array = self._check_vector_dim(new_vector)
            self.vectors[vec_id]['vector'] = new_vec_array
        
        # 更新元数据（支持增量更新，而非覆盖）
        if new_metadata is not None:
            self.vectors[vec_id]['metadata'].update(new_metadata)
        
        print(f"\n🔄 向量ID {vec_id} 更新成功：")
        print(f"   最新向量：{np.round(self.vectors[vec_id]['vector'], 3)}")
        print(f"   最新元数据：{self.vectors[vec_id]['metadata']}")
        return True

    def delete_vector(self, vec_id):
        """
        按ID删除向量
        参数：vec_id - 向量ID
        返回：是否删除成功（布尔值）
        """
        if vec_id not in self.vectors:
            print(f"❌ 向量ID {vec_id} 不存在，删除失败！")
            return False
        del self.vectors[vec_id]
        print(f"\n🗑️  向量ID {vec_id} 删除成功！当前数据库剩余向量数：{len(self.vectors)}")
        return True

    def search_similar(self, query_vector, top_k=5, similarity_threshold=0.0):
        """
        增强版相似度搜索（支持Top-K和相似度阈值过滤）
        参数：
        - query_vector: 查询向量（用户偏好/待匹配向量）
        - top_k: 返回最相似的前K个结果（默认5）
        - similarity_threshold: 相似度阈值（仅返回≥该值的结果，默认0）
        返回：排序后的结果列表（[(ID, 相似度, 元数据), ...]）
        """
        # 校验查询向量维度
        query_array = self._check_vector_dim(query_vector)
        results = []
        
        # 遍历所有向量计算余弦相似度
        print(f"\n🔍 开始相似度搜索（Top-{top_k}，阈值≥{similarity_threshold}）...")
        print(f"   查询向量：{np.round(query_array, 3)}")
        for vec_id, data in self.vectors.items():
            vec = data['vector']
            # 余弦相似度计算：范围[-1,1]，越接近1越相似
            similarity = cosine_similarity([query_array], [vec])[0][0]
            # 过滤低于阈值的结果
            if similarity >= similarity_threshold:
                results.append((vec_id, similarity, data['metadata']))
        
        # 按相似度降序排序
        results.sort(key=lambda x: x[1], reverse=True)
        # 取前K个结果
        top_results = results[:top_k]
        
        # 打印搜索结果
        print(f"✅ 搜索完成，共找到{len(results)}个符合条件的结果，返回前{len(top_results)}个：")
        for idx, (vec_id, sim, meta) in enumerate(top_results, 1):
            print(f"   排名{idx} | ID:{vec_id} | 相似度:{sim:.4f} | 元数据:{meta}")
        return top_results

    def search_with_metadata_filter(self, query_vector, metadata_filter, top_k=5):
        """
        混合搜索：先按元数据过滤，再计算相似度（实战常用）
        参数：
        - query_vector: 查询向量
        - metadata_filter: 元数据过滤条件（字典，如{'genre': '科幻'}）
        - top_k: 返回前K个
        返回：过滤后排序的结果列表
        """
        # 第一步：按元数据过滤向量
        filtered_vectors = {}
        for vec_id, data in self.vectors.items():
            # 检查元数据是否包含所有过滤条件
            match = True
            for key, value in metadata_filter.items():
                if data['metadata'].get(key) != value:
                    match = False
                    break
            if match:
                filtered_vectors[vec_id] = data
        
        if not filtered_vectors:
            print(f"\n❌ 无符合元数据条件{metadata_filter}的向量！")
            return []
        
        # 第二步：对过滤后的向量计算相似度
        query_array = self._check_vector_dim(query_vector)
        results = []
        for vec_id, data in filtered_vectors.items():
            similarity = cosine_similarity([query_array], [data['vector']])[0][0]
            results.append((vec_id, similarity, data['metadata']))
        
        # 排序并返回Top-K
        results.sort(key=lambda x: x[1], reverse=True)
        top_results = results[:top_k]
        
        # 打印结果
        print(f"\n🔍 混合搜索（元数据过滤：{metadata_filter}）结果：")
        for idx, (vec_id, sim, meta) in enumerate(top_results, 1):
            print(f"   排名{idx} | ID:{vec_id} | 相似度:{sim:.4f} | 元数据:{meta}")
        return top_results

    def get_db_stats(self):
        """
        获取数据库统计信息（监控用）
        """
        print("\n📊 向量数据库统计信息：")
        print(f"   向量总数：{len(self.vectors)}")
        print(f"   向量维度：{self.vector_dim if self.vector_dim else '无'}")
        print(f"   最大向量ID：{max(self.vectors.keys()) if self.vectors else '无'}")
        # 打印所有向量的简要信息
        if self.vectors:
            print("   所有向量简要信息：")
            for vec_id, data in self.vectors.items():
                print(f"     ID:{vec_id} | 向量前2位：{np.round(data['vector'][:2], 3)} | 标题：{data['metadata'].get('title', '无')}")

# ====================== 完整使用示例（模拟用户交互流程） ======================
if __name__ == "__main__":
    # ---------------------- 步骤1：初始化向量数据库 ----------------------
    print("="*80)
    print("🚀 初始化简易向量数据库（电影推荐场景）")
    print("="*80)
    movie_store = SimpleVectorStore()

    # ---------------------- 步骤2：批量添加电影向量 ----------------------
    # 电影特征向量定义：[动作强度(0-1), 喜剧程度(0-1), 浪漫程度(0-1), 科幻元素(0-1)]
    movie_vectors = [
        [0.9, 0.1, 0.8, 0.3],  # 星际穿越
        [0.8, 0.2, 0.7, 0.4],  # 盗梦空间
        [0.1, 0.9, 0.2, 0.0],  # 肖申克的救赎
        [0.7, 0.3, 0.1, 0.9],  # 火星救援
        [0.95, 0.05, 0.1, 0.8],# 银翼杀手2049
        [0.2, 0.8, 0.7, 0.1]   # 当幸福来敲门
    ]
    movie_metadata = [
        {'title': '星际穿越', 'genre': '科幻', 'year': 2014, 'score': 9.4},
        {'title': '盗梦空间', 'genre': '科幻', 'year': 2010, 'score': 9.4},
        {'title': '肖申克的救赎', 'genre': '剧情', 'year': 1994, 'score': 9.7},
        {'title': '火星救援', 'genre': '科幻', 'year': 2015, 'score': 8.5},
        {'title': '银翼杀手2049', 'genre': '科幻', 'year': 2017, 'score': 8.3},
        {'title': '当幸福来敲门', 'genre': '剧情', 'year': 2006, 'score': 9.2}
    ]
    # 批量添加
    movie_store.batch_add_vectors(movie_vectors, movie_metadata)

    # ---------------------- 步骤3：查看数据库统计信息 ----------------------
    movie_store.get_db_stats()

    # ---------------------- 步骤4：按ID查询单个向量 ----------------------
    movie_store.get_vector_by_id(0)  # 查询星际穿越

    # ---------------------- 步骤5：更新向量（比如修正星际穿越的评分） ----------------------
    movie_store.update_vector(
        vec_id=0,
        new_metadata={'score': 9.5}  # 只更新元数据，不更新向量
    )

    # ---------------------- 步骤6：基础相似度搜索（模拟用户偏好） ----------------------
    # 用户偏好：喜欢「高科幻、中动作、低喜剧、中浪漫」的电影
    user_preference = [0.85, 0.15, 0.75, 0.35]
    print("\n" + "="*80)
    print("🎯 模拟用户偏好：喜欢高科幻、中动作、低喜剧、中浪漫的电影")
    print("="*80)
    # 搜索相似度≥0.8的前3个电影
    basic_recommendations = movie_store.search_similar(
        query_vector=user_preference,
        top_k=3,
        similarity_threshold=0.8
    )

    # ---------------------- 步骤7：混合搜索（元数据过滤+相似度） ----------------------
    print("\n" + "="*80)
    print("🎯 进阶搜索：只推荐2010年后的科幻电影，且匹配用户偏好")
    print("="*80)
    # 过滤条件：类型=科幻，年份≥2010
    advanced_recommendations = movie_store.search_with_metadata_filter(
        query_vector=user_preference,
        metadata_filter={'genre': '科幻'},  # 先过滤科幻片
        top_k=3
    )

    # ---------------------- 步骤8：删除向量（比如移除测试数据） ----------------------
    movie_store.delete_vector(5)  # 删除当幸福来敲门

    # ---------------------- 步骤9：再次查看数据库统计（确认删除） ----------------------
    movie_store.get_db_stats()

运行结果：

复制代码

================================================================================
🚀 初始化简易向量数据库（电影推荐场景）
================================================================================

📦 开始批量添加6个向量...
✅ 向量ID 0 添加成功 | 元数据：{'title': '星际穿越', 'genre': '科幻', 'year': 2014, 'score': 9.4}
✅ 向量ID 1 添加成功 | 元数据：{'title': '盗梦空间', 'genre': '科幻', 'year': 2010, 'score': 9.4}
✅ 向量ID 2 添加成功 | 元数据：{'title': '肖申克的救赎', 'genre': '剧情', 'year': 1994, 'score': 9.7}
✅ 向量ID 3 添加成功 | 元数据：{'title': '火星救援', 'genre': '科幻', 'year': 2015, 'score': 8.5}
✅ 向量ID 4 添加成功 | 元数据：{'title': '银翼杀手2049', 'genre': '科幻', 'year': 2017, 'score': 8.3}
✅ 向量ID 5 添加成功 | 元数据：{'title': '当幸福来敲门', 'genre': '剧情', 'year': 2006, 'score': 9.2}
✅ 批量添加完成，新增向量ID：[0, 1, 2, 3, 4, 5]

📊 向量数据库统计信息：
   向量总数：6
   向量维度：4
   最大向量ID：5
   所有向量简要信息：
     ID:0 | 向量前2位：[0.9 0.1] | 标题：星际穿越
     ID:1 | 向量前2位：[0.8 0.2] | 标题：盗梦空间
     ID:2 | 向量前2位：[0.1 0.9] | 标题：肖申克的救赎
     ID:3 | 向量前2位：[0.7 0.3] | 标题：火星救援
     ID:4 | 向量前2位：[0.95 0.05] | 标题：银翼杀手2049
     ID:5 | 向量前2位：[0.2 0.8] | 标题：当幸福来敲门

🔍 向量ID 0 查询结果：
   向量值：[0.9 0.1 0.8 0.3]
   元数据：{'title': '星际穿越', 'genre': '科幻', 'year': 2014, 'score': 9.4}

🔄 向量ID 0 更新成功：
   最新向量：[0.9 0.1 0.8 0.3]
   最新元数据：{'title': '星际穿越', 'genre': '科幻', 'year': 2014, 'score': 9.5}

================================================================================
🎯 模拟用户偏好：喜欢高科幻、中动作、低喜剧、中浪漫的电影
================================================================================

🔍 开始相似度搜索（Top-3，阈值≥0.8）...
   查询向量：[0.85 0.15 0.75 0.35]
✅ 搜索完成，共找到2个符合条件的结果，返回前2个：
   排名1 | ID:0 | 相似度:0.9975 | 元数据:{'title': '星际穿越', 'genre': '科幻', 'year': 2014, 'score': 9.5}
   排名2 | ID:1 | 相似度:0.9970 | 元数据:{'title': '盗梦空间', 'genre': '科幻', 'year': 2010, 'score': 9.4}

================================================================================
🎯 进阶搜索：只推荐2010年后的科幻电影，且匹配用户偏好
================================================================================

🔍 混合搜索（元数据过滤：{'genre': '科幻'}）结果：
   排名1 | ID:0 | 相似度:0.9975 | 元数据:{'title': '星际穿越', 'genre': '科幻', 'year': 2014, 'score': 9.5}
   排名2 | ID:1 | 相似度:0.9970 | 元数据:{'title': '盗梦空间', 'genre': '科幻', 'year': 2010, 'score': 9.4}
   排名3 | ID:4 | 相似度:0.7846 | 元数据:{'title': '银翼杀手2049', 'genre': '科幻', 'year': 2017, 'score': 8.3}

🗑️  向量ID 5 删除成功！当前数据库剩余向量数：5

📊 向量数据库统计信息：
   向量总数：5
   向量维度：4
   最大向量ID：4
   所有向量简要信息：
     ID:0 | 向量前2位：[0.9 0.1] | 标题：星际穿越
     ID:1 | 向量前2位：[0.8 0.2] | 标题：盗梦空间
     ID:2 | 向量前2位：[0.1 0.9] | 标题：肖申克的救赎
     ID:3 | 向量前2位：[0.7 0.3] | 标题：火星救援
     ID:4 | 向量前2位：[0.95 0.05] | 标题：银翼杀手2049

七、向量在AI中的深度应用

7.1 自然语言处理（NLP）：词嵌入

词嵌入是NLP的核心，将每个词映射到高维向量空间，且语义相近的词向量距离更近：

python 复制代码

# 经典向量关系示例
# 国王 - 男人 + 女人 ≈ 女王
king_vec = np.array([0.15, -0.32, 0.47, ..., 0.21])   # 300维
man_vec = np.array([0.18, -0.35, 0.42, ..., 0.24])
woman_vec = np.array([0.12, -0.31, 0.48, ..., 0.20])
queen_vec = king_vec - man_vec + woman_vec  # 近似女王向量

这种语义推理能力，正是向量空间几何特性的体现。

7.2 推荐系统：用户-物品向量匹配

推荐系统的核心逻辑是"向量相似度匹配"：

python 复制代码

# 简化版推荐逻辑
def recommend_items(user_id, top_k=10):
    # 1. 获取用户向量
    user_vector = get_user_embedding(user_id)
    # 2. 获取所有物品向量
    item_vectors = get_all_item_embeddings()
    # 3. 计算相似度并排序
    similarities = [cosine_similarity([user_vector], [v])[0][0] for v in item_vectors]
    # 4. 返回Top-K
    top_indices = np.argsort(similarities)[-top_k:][::-1]
    return [item_ids[i] for i in top_indices]

7.3 计算机视觉（CV）：特征提取

卷积神经网络（CNN）提取图像特征的本质，是将图像转换为高维向量：

输入层：图像像素向量；
卷积层：提取边缘、纹理等低级特征向量；
全连接层：组合为高级语义向量；
输出层：基于向量进行分类/检索。

7.4 向量数据库：AI时代的记忆系统

传统数据库做精确匹配 ，向量数据库做相似度匹配：

sql 复制代码

-- 传统SQL（精确匹配）
SELECT * FROM products WHERE name = '智能手机';

-- 向量查询（相似度匹配）
-- 找到与用户兴趣向量最相似的10个产品

八、写在最后：向量，是AI与现实世界的翻译官

下次当你：

用Face ID解锁手机
收到"刚好想要"的商品推荐
和聊天机器人流畅对话

请记得：在这些智能体验的背后，有一个个向量正在高维空间中旋转、靠近、计算、决策。

向量不是数学的终点，而是AI理解人类世界的起点。

💌 博主寄语 ：

技术可以复杂，但理解不必困难。

希望今天的分享，让你看到数学的温度，也感受到AI的逻辑之美。

如果你觉得有收获，欢迎点赞、转发，也欢迎在评论区告诉我：你还想了解哪些AI背后的"隐藏英雄"？

我们下期见！✨

进阶篇-4-数学篇-3--深度解析AI中的向量概念：从生活到代码，一文吃透核心逻辑

深度解析AI中的向量：从一杯奶茶到神经网络的"数字心跳"

一、生活中的向量：你以为的"描述"，其实是"数据"

🌰 用向量描述"一杯奶茶"

更多生活化例子：

二、向量在AI中的三大核心角色

角色1：数据的"通用身份证"

角色2：相似度的"度量尺"

🌰 场景1：推荐系统

🌰 场景2：人脸识别

角色3：特征的"组合积木"

三、向量的数学本质：从几何直觉到高维空间

3.1 什么是向量？

3.2 直观理解

二维空间（可可视化）

高维空间（AI中的现实）

四、用生活中的猫，狗和冰箱进一步认识计算机中的向量

4.1 🧠 背景设定：我们用8个"语义特征维度"描述物体

4.2 🐱🐶🧊 计算机中三类对象的可能8维向量

🔍 逐维度解读：

4.3📏 计算向量距离，看计算机认为谁和谁长得更像（用欧氏距离）

1. 猫 vs 狗 的距离

2. 猫 vs 冰箱 的距离

3. 狗 vs 冰箱 的距离（类似）

✅ 结论：猫和狗很近，它们和冰箱很远！

4.4 🐈🐈‍⬛ 再深入：不同猫品种之间距离更近！

1.计算距离：

2.更合理的设定（强调"同种更近"）：

4.5 🌌 总结：向量如何表达"语义相似性"

希望这个充满生活气息的例子，让你真正"看见"了向量的语义力量！

五、向量的核心计算：AI中最常用的4类操作

5.1 向量加法："特征叠加"

5.2 向量点积（内积）："相似度计算"

5.3 向量的L2范数（模长）："特征强度"

5.4 向量距离（欧氏距离）："差异度计算"

5.5 余弦相似度："方向一致性"

六、Python实战：用代码让向量"活"起来

6.1 基础向量操作（加法/点积/范数/距离）

6.2 相似度计算实战（推荐系统核心）

6.3 文本向量化实战（NLP核心）

6.4 图像向量化实战（CV核心）

6.5 简易向量数据库实现（AI检索核心）

七、向量在AI中的深度应用

7.1 自然语言处理（NLP）：词嵌入

7.2 推荐系统：用户-物品向量匹配

7.3 计算机视觉（CV）：特征提取

7.4 向量数据库：AI时代的记忆系统

八、写在最后：向量，是AI与现实世界的翻译官

1. 猫 vs 狗的距离

2. 猫 vs 冰箱的距离

3. 狗 vs 冰箱的距离（类似）