《智能的理论》全书转至目录****
不同AGI的研究路线对比简化版:《AGI(具身智能)路线对比》,欢迎各位参与讨论、批评或建议。
人类具有对刺激的非符号数量(11-6:数)进行表征的能力,即对物体的数量进行判断的能力,这种能力也被称为数量枚举。非符号数量的数量枚举加工方式有三种:感数、估计、计数。
一.数量枚举
在数的感知中存在着这样一种现象。当呈现的客体数量为1-3个时,人们能快速的对客体数量进行判断。在相关实验中,当客体数量落在1-3个时,哪怕只呈现100ms,被试仍然能快速准确的识别出来。且每增加一个客体,被试的反应时间仅增加50-80ms。当呈现的客体数在4个或者4个以上时,被试的反应时间随客体个数的增加而增加,约每增加一个客体就增加200ms的反应时间,且数量判断准确率下降(Kaufman,1949;Mandler和Shebo,1982;Trick和Pylyshyn,1993)。
数量枚举是对刺激总数进行判断的过程(Shimomura和Kumada,2011)。根据上述现象,非符号数量的数量枚举方式有三种,一种是对小数(1-3个)进行快速准确的感知策略,被称为感数(Kaufman,1949)。感数的加工策略可能有其环境适应性意义。当动物能够区分2个和3个天敌时,它们在环境中的生存拥有更大的优势;反之, 区分92个和93个天敌则不会有如此大的意义(Beran,2008);当数量较大(>4)且用于判断的时间不足时,被试就会对刺激数量进行近似估计,估计准确率随数量的增大而减少,这种对大数的快速且不准的估计策略称为估数;当数量较大且时间充足时,被试则依赖序列计数。对感数而言,既可认为使用精确数表征系统,也可认为使用近似数表征系统(小数值范围内的近似数表征也较为准确);估数使用近似数表征系统;计数使用精确数表征系统。
二.感数
为了解释感数现象,不同的研究者提出了不同的理论。其中一种站在工作记忆容量有限的角度(Miller,1956),认为由于工作记忆可以储存的信息量是有限的,当客体数量在工作记忆范围内(如小于4),工作记忆能对客体进行直接存储,因此使用感数策略。当超出了工作记忆的容量范围时,加工过程就会受到限制,从而转用计数方式。而FINST理论认为,标记数量一般为4个。当刺激数量不超过4个时,可以使用已经使用的标记直接获取数量信息(使用了多少标记就有多少个客体),因此当刺激数量为1-3个时被试的反应时间增加不明显。
三.估数
数量范围在1-4个时数量估计又快又准,而数量超出4个时错误率陡然递增。研究者将这两个数量范围称为小数和大数。对于小数和大数的分离,一些研究者仍然认为它们同属于一个系统,近似表征系统。这种分离实际上仍然符合韦伯定律(即这种分离仍然符合近似数表征系统的特征),即当数值较小时(1-4),实际数量和心理数量大致相等,符合线性性(小数时对数表征和线性表征相似。换句话说,对数表征的小数部分可看作线性);当数值较大时(>4),实际数量和心理数量的差异指数增大(Gallistel和Gelman,1991)。
1.刺激表面特征对估数的影响
通过视觉,人和动物拥有对物体的数量进行估计的能力,同时也有判断不同数量之间关系的能力(比如那一边的数量多)。一些研究认为,物体的表面特征(如面积大小、形状、颜色、空余面积等非数量特征)会影响数量的感知。例如,Sophian(2007)的研究发现,刺激(面积)大小对数量判断有显著影响,当刺激点数相同时被试倾向于认为较小的刺激点有更多的数量。在Piazza和Izard(2004)等人的研究下,发现存在专门针对特定数量进行反应的神经元,这说明存在专门针对数量感知的特征,即数量特征。那么,这些特征(物体的表面特征和数量特征)到底是如何影响着数量的感知呢?
刘炜等人(2013)对此进行了实验。实验对被试同时呈现两张图,左右两张并列呈现(如图1(a))。一张为包含81个客体的恒定刺激,另外一张为比较刺激。比较刺激包含的客体可能为60、67、74、90、99、110。两张图片的呈现时间为500ms,呈现结束后需要被试判断那边的图片呈现的客体数量多。为了弄清楚是那种因素影响着数量感知,实验对恒定刺激进行6种设置(图1(b))。包括控制条件,这种条件下恒定刺激为随机分布的黑白方块;大小对比条件,其客体面积对比控制条件的小;形状对比条件,此时客体的形状从方块变为圆;均匀分布条件,恒定刺激从随机分布改为均匀分布;组块条件1,恒定刺激为9个随机分布的圆形点阵,每个点阵均由9个黑色或白色方块组成,共81个方块;组块条件2,恒定刺激为9个随机分布的方块点阵,每个点阵均由9个黑色或白色方块组成。组块条件2下点阵的密度比组块条件1的高。在所以条件下,比较刺激均为随机分布的黑色或白色方块。通过实验结果和其他的一些研究可以得出下面两个结论。
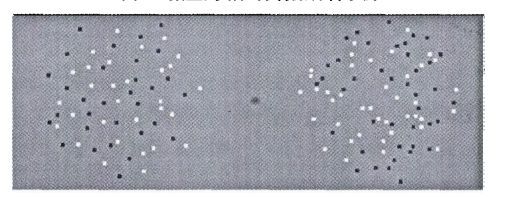
图1(a)

图1(b)
大小对比条件,形状对比条件和均匀分布条件其数量判断的辨别力对比控制条件差异不大。这说明,客体的表面特征(如大小、形状等非数量特征)对数量感知的影响并不显著。一些研究发现(Sophian,2007)发现,对比大刺激,相同数量的情况下小刺激会被感知到更多的数量。Sophian和chu(2007)在论文中分析到,大小、空间分布和客体之间的空白间隔等因素对数量感知的影响,是被试在测试过程中结合了自身的生活经验进行推断的,即通常情况下小的刺激数量会更多。De Hevia(2011)认为,可以将视觉线索和数量信息的加工视为并行的过程,数量感知的主要因素是数量特征,并在一定程度上受到了视觉线索的影响,目的大部分研究支持这一观点。
对于组块条件(1和2),其数量判断的辨别力对比控制条件会显著的下降。这可能是由于格式塔的邻近性使相邻的客体组织成为一个更大的客体,它们会被作为一个整体的存在,从而感知的数量大大减少(点阵数量为9,客体数量为81)。另外,组块条件2的数量辨别力比其条件1的会变得更差。这可以认为,因为点阵更为稠密,所以被感知为一个整体的倾向更为强烈。类似的,当使用线将两个客体联结在一起时,根据格式塔的一致联通性,这两个联结在起来的客体看起来更像是一个整合的客体,因此被试对客体数量的感知会显著减少(He et al,2009)。而Halberda等人(2006)发现,当客体按照不同颜色进行分组时,被试的数量感知同样会显著减少,并且数量判断偏向于分组的数量。
2.数量感知的意识水平(刘炜,2013)
一些研究认为,人们对场景的数量信息具有直接的感受性,它是一种初级的视觉特征(Burr和Ross,2008),属于无意识处理的范畴。而在另外一些研究又认为它属于意识处理的范畴,比如"空间数字联合编码效应"(11-6:数,如"数量多与空间的上部或右部联系"),它只能存在于更高级的神经元中。那么数量感知到底是属于那种意识范畴的呢?
刘炜(2013)采用数量的适应后效和视觉后效的双眼传递特性两种技术研究了意识和数量感知的关系。数量的适应后效是指,当观察者对某一区域客体的数量进行观察时,会导致该区域数量感知的变化。具体的说,之前某一区域存在数量较多(少)的客体,在观察过后,对该区域所感知客体的数量会减少(增多)(Burr和Ross,2008)。视觉后效的双眼传递特性是指,当刺激只呈现在一只眼时(即观察眼)(另外一只眼不看,不看的眼称为非观察眼),刺激的某一特征产生的适应后效可以从观察眼传递到非观察眼。即当在观察眼中产生了适应,如果非观察眼也能观察到这种适应现象,说明适应产生了双眼传递。相反,如果只有观察眼有这种适应后效,而非观察眼没有这种适应后效,则是单眼内传递。视觉后效的双眼传递主要依赖较高水平的神经细胞,反映较高的意识加工水平;单眼内传递则涉及简单神经细胞完成,反应较为自动化的加工水平(Sweeny,Grabowecky和Suzuki,2011)。另外,非观察眼的适应程度越高,说明意识的参与水平越高;反之则越低(Durgin,2001)。因此,根据数量适应后效是双眼适应还是单眼内适应,就能判断数量感知处于什么意识水平。
在一项实验中(刘炜,2013),分别设置了非意识组和意识组,每一组又分为有适应和无适应两种条件。对于非意识组的有适应条件流程如下:在学习阶段,会对被试呈现1000ms的适应刺激。被试使用双竞争仪进行观察,观察眼会观察到两组点集刺激,两组点集互为上下位置关系,上方呈现405个客体,下方呈现5个。非观察眼会观察到10张不规则的彩色图,每张呈现100ms,共1000ms(图2(a))。呈现不规则彩图的目的是为了分散被试的注意,从而降低被试在观察眼的意识。在测试阶段,首先呈现200ms的比较刺激,刺激处于观察眼的上方(即包含405个适应点的点集处),其客体数量分别为20、27、33、40、49、60、74和90。接着呈现200ms的恒定刺激,处于观察眼的下方(即包含5个的适应点的点集处),其客体数量为30个。所以客体均为随机分布的黑白方块。整个过程如图2(b)所示。对于非意识组的无适应条件,学习阶段改为适应刺激的观察眼部分呈现灰色空屏,非观察眼部分同样呈现10张不规则彩图。对于有意识组的适应条件,在学习阶段,适应刺激的观察眼部分呈现上下两组点阵,与非意识组且有适应一致。而非观察眼不再呈现10张不规则的彩色图,改为灰色空屏代替。对于有意识组的无适应条件,在学习阶段,适应刺激的观察眼和非观察眼部分均呈现灰色空屏。

图2(a)
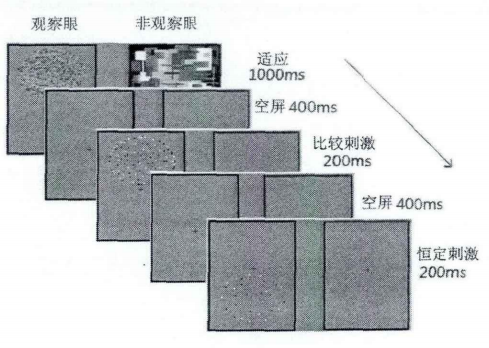
图2 (b)
在测试阶段,被试需要做的是,分别用观察眼和非观察眼对测试刺激进行观察,判断那个位置(上方还是下方)的客体数量多。实验的目的是通过视觉后效的双眼传递特性来测试数量感知与意识的关系。根据数量适应理论,在适应条件下,因为观察眼上方的适应点数较多(405个),所以在该处适应后会低估比较刺激数量;又因为观察眼下方的适应点较少(5个),所以在该处适应后会高估恒定刺激的数量。
从适应条件的实验结果发现,不论是意识条件下还是非意识条件,在实验中该数量适应现象都可以在观察眼中被发现。即需要对被试的观察眼呈现更大数量的比较刺激,被试才会认为比较刺激的客体数量大于恒定刺激。且意识条件下的数量会比非意识条件下的更大。比如,具体的说,大概需要对被试呈现大于49或者60个客体的比较刺激,被试才可能认为比较刺激大于恒定刺激,而在非意识条件下,只需对被试呈现大于40个。这说明,在观察眼中非意识和意识条件均发生了数量适应,且意识条件下该现象更明显。
在非观察眼中,数量适应只在意识条件下发生了,而在非意识条件下无法观察到这种适应后续的现象。在实验中体现为,在意识条件下,大概需要对被试呈现大于49或者60个客体的比较刺激,被试才会认为比较刺激大于恒定刺激,而在非意识条件下则需大于27或33个。这说明,意识条件下数量特征发生了视觉后效的双眼传递特性,而非意识条件没有。
总的来说,数量感知在两种加工水平均有发生。
四.计数
1.语言计数
Pica等人(Pica,Lemer,Izad和Dehaene,2004)在对亚马孙的两个部落Piraha和Munduruku的数字能力进行研究后发现,这两个部落只有能表征1-5数量的语言,当数量超过5时他们只能使用"一些"或"许多"等词语。因此,当数量超过5时,由于缺乏语言计数机制,所以他们无法识别出5以上的数量。
Dehaene等人(Dehaene,Spelke,Pinel,Stanescu和Tsivkin,1999)通过数学加法研究语言习得与数字处理的关系,实验过程如图3所示。该研究包括两种加法条件,第一种是精确值加法条件,即先呈现一个简单加法(如4+5),之后呈现两个数字(9和7),其中一个数字是加法之和(9),被试需要判断这两个数字哪个是加法的和(4+5=9);第二种是近似值加法条件,先呈现一个简单加法(如4+5),然后呈现两个数字,这两个数字均不是加法之和(8和3),而被试需要选择出最接近加法和的一个(即8)。该研究也包括两种语言条件,俄语和英语。在进行测试前,需要使用该流程对被试进行训练(让被试熟悉流程)。实验结果表明,在精确值加法条件下,当训练和测试所使用的语言是一致的情况时(都是俄语或都是英语),被试在测试过程中的反应时间要明显低于语言不一致的情况。而在近似值加法条件下,训练和测试所使用的语言是否一致对被试的反应时间没有影响。这说明了,精确值运算需要依赖后天语言,而近似值运算不依赖后天语言。
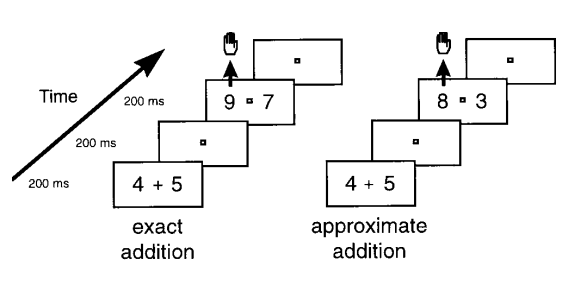
图3
2.非语言计数
Cordes(Cordes,Gelman和Gallistel,1983)将被计数的刺激比喻成杯子中的液体,每个刺激可比喻成一个装有液体的杯子。每个刺激都会使累计器累计激活,即当刺激项目越多时累计器的激活程度就越大。累计器可以比喻为一个大的容器,可存储杯子中的液体。当杯子越多时,容器中的液体就越多。场景客体的数量与累计器呈线性关系。累计器的激活程度可以与存储在记忆中的激活程度相比较。或者说,累计器处于不同激活程度对应不同数值的符号。当累计器的某一激活程度对应于某一符号时,该符号的数值就是计数得到的数值。又因为刺激在记忆中的数量感是波动的和变化的,所以这种非语言计数是不准确的。如图4。该模型被称为模拟量模型(又称为累加器模型)。
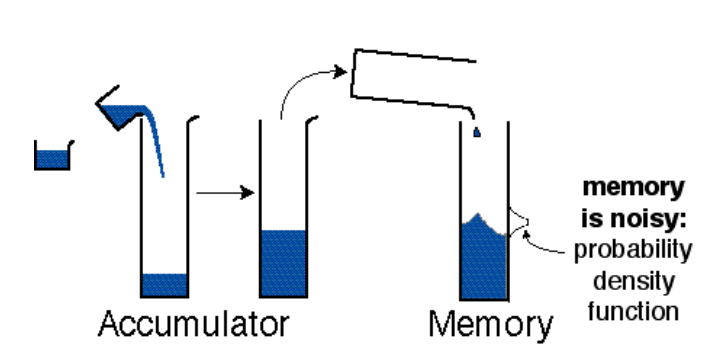
图4
3.FINST理论
Pylyshyn利用FINST理论对感数和计数进行解释。当需要进行数量枚举时,首先要做的是将每个客体从视野中分离出来,使之成为一个个独立的个体。之后FINST会对每个客体进行标记。因为FINSTs的标记数量有限,所以当目标客体个数小于FINSTs的总标记数时,便启动感数加工。反之,则启用计数加工。感数加工是数字再认或数字反应选择,即将已使用的标记数量与记忆中储存的数字名称相匹配即可。计数包括三个过程:第一,确定不能够进行感数加工(如上述,当目标客体的数量少于FINSTs的总标记数量时);第二,将客体分成不同的组,每组的数量不能超过总标记的数量(4个以内);第三,对不同组进行扫描,采用感数策略算出每一组的客体数量,并对以被计数的项目进行"注释"表明这些客体以被计数,随即将注意转移到下一未注释的组中,最后算出总的客体数量。(徐晓东和刘昌,2007)
4.计数模型
Verguts和Fias(2004)提出了计数模型,该模型能够提取这两种形式的数。对于非符号形式的数的感知,需要经过数量易感阶段和数量选择阶段。数量易感阶段是一种自动化无意识的过程,它又可以分为客体位置映射子阶段和总和编码子阶段。
客体位置映射相当于视网膜上的一个标记过程,即对视网膜中的目标客体进行标记,并且有多少客体标注多少个。使它们与背景进行分离并且成为一个独立的个体。这种标记对目标的表面特征不敏感,即不管它是苹果还是老虎,只将目标所在的位置进行标记。如图5中从视网膜中标记了的三个客体。
总和编码有一个较大的感受野,它接受来自于客体位置映射过程中的位置标记,并对这些位置标记进行累积。不同的总和编码细胞其特性不同,一些总和编码细胞的激活程度随标记数量单调递增(标记数量越多,激活程度越高,类似于温度计是一种连续的变化),另外一些随着标记数量单独递减。因此,每个总和编码细胞都包含了标记数量信息。如图5,当标记数量为3时,(单个)总和编码细胞累计激活强度也为3。这种编码方式能解释距离效应,因为当(标记)数量相似时,总和编码也相似,从而难以区分。也能解释大小效应,对于很大的数量,不管多大,一些单调递增的细胞激活程度趋近与饱和,如数量为500时某细胞激活程度以饱和,数量为600时该细胞激活程度也是饱和;另外,某些单调递减的细胞激活程度也会趋近与静止。因此,对于越大的数字,总和编码越相似。
在数量选择阶段(也叫位置编码),完成我们对数量的感知。它接收来自于总和编码细胞的信号,不同的总和编码信号强度会激活不同的数量神经元。位置编码包含一系列的只对特定数量反应的神经元。如一些神经远只对数量10有最大反应,一些神经元只对数量23有最大反应的...。当数量离特定数量越远时,该神经元的反应就越弱。如图5,表征3的总和编码激活了表征3的数量编码,使其激活程度最大。而表征2和表征4的数量编码也有一定程度的激活(但比3小),如此类推。
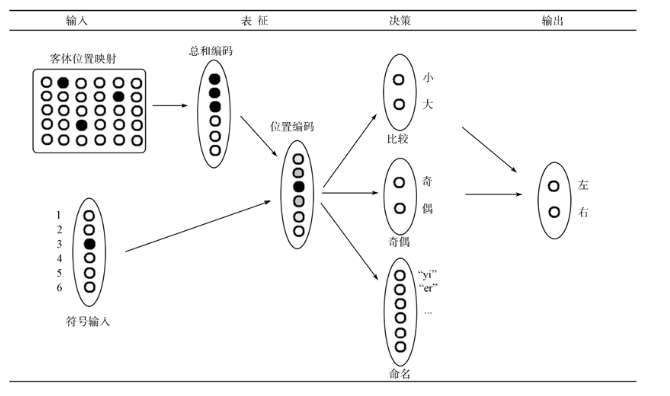
图5
对于符号数的感知,则直接省去了客体位置映射和总和编码,它能直接激活位置编码。符号和特定的位置编码之间的联系是通过后天学习而得的。
五.密度估计(刘炜,王苗,张智君和赵亚军,2016)
数量估计(估数)和密度估计的关系是数量认知研究的关键问题。但数量估计与密度估计即有联系又有区别,即数量特征描述了一定区域内的客体的多少,它等于密度乘以面积,在给定的面积内, 客体的数量决定了客体的密度。
一种观点认为,观察者在密度加工的基础上,根据任务要求推测数量。数量认知能力没有独立的机制,它只是密度加工的副产品(Durgin,2008)。观察者通过面积大小和密度特征来计算数量的,有研究发现直接的数量感知并不如感知面积和感知密度那么准确(Dakin,Tibber,Greenwood和Kingdom等人,2011)。
另外一种观点是由刘炜等人提出的假设(刘炜,王苗,张智君和赵亚军,2016),即数量加工即涉及初级加工(无意识)也涉及高级加工(有意识)(如上述),其中初级加工阶段就是密度感知过程。首先,上面已经证明了数量加工同时包含初级和高级的加工过程;其次,数量和密度共享初级加工阶段。Anobile等人(Anobile,Cicchini和Burr,2014)的研究发现,当刺激密度适中时,无论要求被试进行数量判断还是密度判断,任务中韦伯分数(11-6:数)的模式都是一致的,表明被试对数量和密度两种加工均调动了同一种辨别机制;但当刺激密度变大时,数量加工的韦伯分数表现出新的模式,提示高密度刺激抑制了数量加工,只激活密度加工。造成这种现象的可能原因是:认知系统难以从高密度刺激中分离和表征个别的客体。这表明,密度加工和数量加工既有相同机制又有不同机制;最后,密度加工仅是数量加工的初级加工过程。数量加工发现适应后效的双眼传递特性和"空间数字联合编码效应"等高级加工过程,而密度加工则没有这种现象,它只有单眼内传递特性(Liu,Zhang,Zhao和Liu,2013)。