第三步--根据python基础语法完成一个简单的深度学习模拟

赤狐先生2026-01-24 10:18

完成一个根据一个 恋爱次数推理模拟 y= wx+b

随机给出 w 和 b ，根据数据集求出真正满足条件的w 和 b

以下是示意图

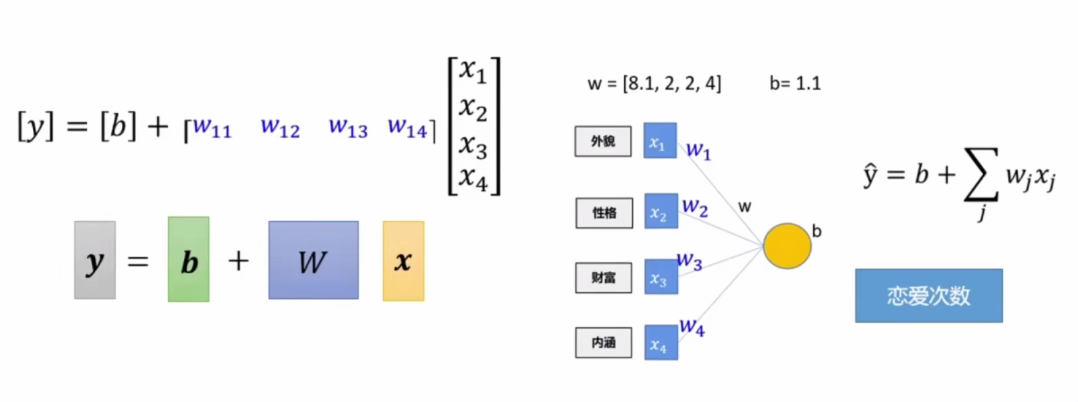
x是四大因素

一，先创造出数据集 -- 多组（x和y）

1.x应该是一个矩阵，行列分别是数据的个数和 w的维度

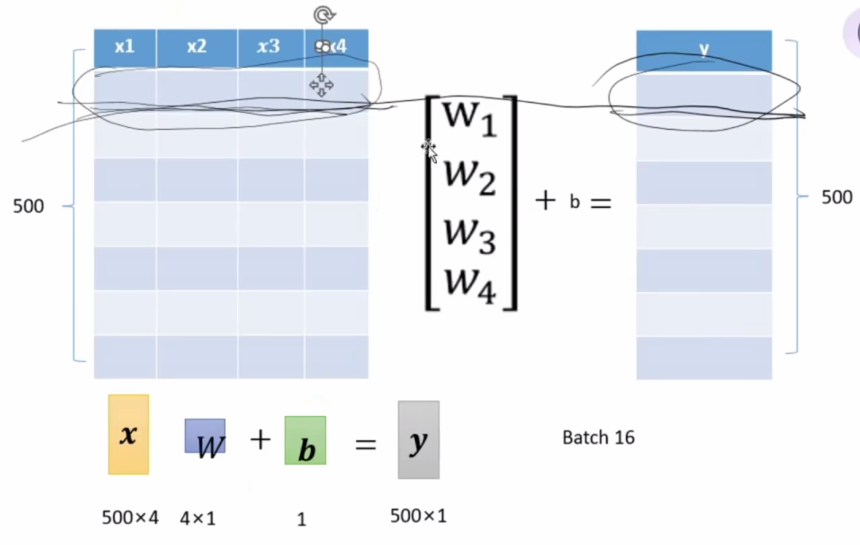
下面给大家一个基于这个模型，生成随机数的代码

python 复制代码 
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
import torch
import matplotlib.pyplot as plt # 画图的
import random

def creat_data(w,b,data_num): # 生成数据集
    # 生成一个服从"正态分布（高斯分布）"的随机矩阵，作为模型的输入特征X
    x = torch.normal(0, 1, (data_num,len(w))) # 平均值0， 标准差1，行为数量数，列为w向量长度(维度）
    y = torch.matmul(x, w) +b  # matmul 表示矩阵相乘

    noise = torch.normal(0, 0.01, y.shape) # 噪声要加在y上
    y += noise

    return x, y

num = 500
true_w = torch.tensor([8.1, 2, 2, 4])
true_b = 1.1


X, Y = creat_data(true_w, true_b, num)

plt.scatter(X[:, 0], Y, 1)  # 画一个散点图
plt.show()

1.2获取数据完整代码

python 复制代码 
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
import torch
import matplotlib.pyplot as plt # 画图的
import random

# --- 第一部分：制造数据的工厂 ---
def creat_data(w,b,data_num): # 生成数据集
    # 生成一个服从"正态分布（高斯分布）"的随机矩阵，作为模型的输入特征X
    x = torch.normal(0, 1, (data_num,len(w))) # 平均值0， 标准差1，行为数量数，列为w向量长度(维度）
    # 生成 Y: 矩阵乘法 + 偏置
    y = torch.matmul(x, w) +b  # matmul 表示矩阵相乘
    # 加点噪声，模拟真实世界的不完美
    noise = torch.normal(0, 0.01, y.shape) # 噪声要加在y上
    y += noise

    return x, y


# --- 第二部分：数据分发器 (Data Provider) ---
# 作用：把一大堆数据切成小块（Batch），每次喂给模型一口
def data_provider(data, label, batchsize): # 每次访问这个函数，就能提供
    length = len(label)  # 获取样本总数 # 总数据量，例如 500
    indices = list(range(length))  # 创建0~n-1 500 的索引列表 生成索引列表 [0, 1, 2, ... 499]

    # 打乱索引：为了随机梯度下降(SGD)，每次读取顺序最好是乱的
    random.shuffle(indices)

    # 步长循环：0, 16, 32, 48...
    for each in range(0, length, batchsize):
        # 1. 拿到这一批的"身份证号"（索引）
        get_indices = indices[each: each+batchsize]
        # 2. 根据身份证号去拿数据 (Tensor 的花式索引功能)
        get_data = data[get_indices]
        get_label = label[get_indices]

        # 3. 把这一小批数据"交"出去，并暂停函数执行，等待下一次召唤
        yield get_data, get_label # 有存档点的return

# batchsize = 16
# for batch_x, batch_y in data_provider(X, Y, batchsize):
#     print(batch_x, batch_y)
#     break

def fun(x, w, b)

# --- 第三部分：主程序执行逻辑 ---
# 1. 定义真实的规律 (上帝视角)
num = 500
true_w = torch.tensor([8.1, 2, 2, 4])
true_b = 1.1

# 2. 创造数据 (X 和 Y 都在这里生成好了)
X, Y = creat_data(true_w, true_b, num)

# 3. 模拟训练过程
batch_size = 16  # 我们决定每次给模型看 16 条数据
print("开始读取数据...\n")
# data_provider 返回的是一个生成器，我们可以直接用 for 循环遍历它
for batch_x, batch_y in data_provider(X, Y, batch_size):
    # 这里就是未来你写"模型训练"和"梯度下降"的地方
    print(f"取出一批数据：X的形状 {batch_x.shape}, Y的形状 {batch_y.shape}")

    # 打印其中一个具体的数值看看
    # print(batch_x[0], batch_y[0])
print("\n数据读取完毕！")

# 4. 画个图看看（依然画第0列）
plt.scatter(X[:, 0], Y, 1)
plt.show()

二、将数据应用于学习

数据已经准备好了（就像我们要分析的几百个恋爱案例），现在我们需要构建一个"大脑"来学习这些数据背后的规律。

2.1 定义核心组件

在开始训练之前，我们需要定义三个关键函数：

  • 模型函数 (fun)：根据输入的X（颜值、才华等因素）和当前的权重W、偏置b，猜测结果Y。

  • 损失函数 (meaLoss)：判断刚才猜得有多离谱？（预测值和真实值的差距）。

  • 优化器 (sgd)：根据差距，反向调整W和b（知错能改）。

python 复制代码 
# --- 模型定义 ---
# 根据 x, w, b 计算预测的 y
def fun(x, w, b):
    pred_y = torch.matmul(x, w) + b
    return pred_y  # 返回预测的 y

# --- 损失函数 (Loss Function) ---
# 这里使用平均绝对误差 (Mean Absolute Error)，计算预测值和真实值的平均距离
def meaLoss(pre_y, y):
    return torch.sum(abs(pre_y - y)) / len(y)

# --- 优化器 (SGD - 随机梯度下降) ---
# 核心逻辑：参数 = 旧参数 - 学习率 * 梯度
def sgd(paras, lr):
    with torch.no_grad(): # 告诉PyTorch：接下来的更新操作不要记录进"计算图"，省内存且避免死循环
        for para in paras: # 遍历列表，先取出 w，再取出 b
            # 核心更新公式：朝着梯度的反方向走一步
            para -= para.grad * lr

            # 梯度清零
            # 类似于 C++: p->grad->reset();
            # 重要！如果不清零，下一轮计算的梯度会累加在旧梯度上，导致方向全错
            para.grad.zero_()

2.2 初始化参数

在最开始，模型什么都不知道，所以我们随机给它一组权重 www 和偏置 bbb。这就好比一个刚出生的婴儿，对"恋爱规律"一无所知，只能瞎猜。
关键点： 必须设置 requires_grad=True，告诉 PyTorch 这两个变量是需要求导（计算梯度）的。

python 复制代码 
lr = 0.01 # 学习率：决定了我们要改得多快，太大容易改过头，太小则学得慢
# 随机初始化 w，形状必须和真实的 true_w 一样
w_0 = torch.normal(0, 0.001, true_w.shape, requires_grad=True)
# 初始化 b 为 0.01
b_0 = torch.tensor(0.01, requires_grad=True) 

print("初始随机权重:", w_0)
print("初始随机偏置:", b_0)

2.3 训练循环 (Training Loop)

这是最激动人心的部分！我们将进行 50 轮（Epochs）的学习。每一轮里，我们都会把所有数据通过 data_provider 分批喂给模型。

学习流程四部曲：

  1. Forward (前向传播)：用当前的 w0,b0w_0, b_0w0,b0 算出一个预测值。
  2. Loss (计算损失)：看预测值和真实值差多少。
  3. Backward (反向传播)：loss.backward()，PyTorch 自动帮你算出每个参数该怎么调（计算梯度）。
  4. Update (参数更新)：调用 sgd 修改 w0w_0w0 和 b0b_0b0。
python 复制代码 
epochs = 50  # 训练轮数：把所有书看50遍

for epoch in range(epochs):
    data_loss = 0 # 记录这一轮的总误差
    
    # 每次取一个 batch (16条数据) 进行训练
    for batch_x, batch_y in data_provider(X, Y, batch_size):
        # 1. 预测
        pred_y = fun(batch_x, w_0, b_0)
        # 2. 算差距
        loss = meaLoss(pred_y, batch_y)
        # 3. 反向传播 (求梯度)
        loss.backward()
        # 4. 更新参数
        sgd([w_0, b_0], lr)
        
        data_loss += loss # 累加 loss 用于观察打印

    # 每学完一轮，打印一下当前的误差
    print("epoch : %03d: loss:%.6f" % (epoch, data_loss))

三、结果验证与可视化

训练完成后，我们要来看看模型学到的 w0w_0w0 和 b0b_0b0（也就是它总结出的恋爱公式），是不是接近上帝视角的 true_w 和 true_b。

3.1 数值对比

python 复制代码 
print("-" * 30)
print(f"真实的 w 值是: {true_w}")
print(f"训练出的 w 值是: {w_0.data}") # .data 可以只看数值，不看梯度信息
print("-" * 30)
print(f"真实的 b 值是: {true_b}")
print(f"训练出的 b 值是: {b_0.data}")

如果代码运行正常，你会发现训练出的值和真实值非常接近！这说明模型通过看数据，反推出了公式。

3.2 可视化拟合效果

最后，我们画一张图来看看拟合效果。因为 XXX 有4个维度（4个特征），我们没法画5维空间图，所以我们只取 第0列特征 来画一个平面图，看看模型学到的直线（红线）是否穿过了数据点（蓝点）。
注意：matplotlib 不能直接画 PyTorch 的 Tensor，需要用 .detach().numpy() 把数据从计算图中剥离出来转成数组。

python 复制代码 
# 我们只观察第 0 个特征（即第一列数据）与结果之间的关系
idx = 0

# 1. 散点图：真实的观测数据
plt.scatter(X[:, idx], Y, 1, label="True Data")

# 2. 折线图：模型的预测结果
# 核心逻辑：y = w[0] * x[0] + b
# 这里我们手动用学到的 w_0 和 b_0 算一遍预测直线
x_axis = X[:, idx].detach().numpy()
y_pred_line = x_axis * w_0[idx].detach().numpy() + b_0.detach().numpy()

plt.plot(x_axis, y_pred_line, color='red', label="Prediction Model")
plt.legend() # 显示图例
plt.show()

(注：此处可插入你运行代码后生成的直线拟合图)

总结

通过这套代码，我们从零开始实现了一个线性回归模型：

  • 数据层：手动制造了带噪声的 y=wx+by = wx+by=wx+b 数据。
  • 模型层：用矩阵乘法实现了预测逻辑。
  • 训练层：手写了 SGD 梯度下降，没有依赖 PyTorch 的 nn.Linear 或 optim.SGD 高级API。

这正是深度学习最底层的原理：通过大量的数据迭代，不断调整参数，让数学公式去逼近现实世界的规律。

综合代码

python 复制代码 
import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'
import torch
import matplotlib.pyplot as plt # 画图的
import random

# --- 第一部分：制造数据的工厂 ---
def creat_data(w,b,data_num): # 生成数据集
    # 生成一个服从"正态分布（高斯分布）"的随机矩阵，作为模型的输入特征X
    x = torch.normal(0, 1, (data_num,len(w))) # 平均值0， 标准差1，行为数量数，列为w向量长度(维度）
    # 生成 Y: 矩阵乘法 + 偏置
    y = torch.matmul(x, w) +b  # matmul 表示矩阵相乘
    # 加点噪声，模拟真实世界的不完美
    noise = torch.normal(0, 0.01, y.shape) # 噪声要加在y上
    y += noise
    return x, y


# --- 第二部分：数据分发器 (Data Provider) ---
# 作用：把一大堆数据切成小块（Batch），每次喂给模型一口
def data_provider(data, label, batchsize): # 每次访问这个函数，就能提供两组数据
    length = len(label)  # 获取样本总数 # 总数据量，例如 500
    indices = list(range(length))  # 创建0~n-1 500 的索引列表 生成索引列表 [0, 1, 2, ... 499]

    # 打乱索引：为了随机梯度下降(SGD)，每次读取顺序最好是乱的
    random.shuffle(indices)

    # 步长循环：0, 16, 32, 48...
    for each in range(0, length, batchsize):
        # 1. 拿到这一批的"身份证号"（索引）
        get_indices = indices[each: each+batchsize]
        # 2. 根据身份证号去拿数据 (Tensor 的花式索引功能)
        get_data = data[get_indices]
        get_label = label[get_indices]

        # 3. 把这一小批数据"交"出去，并暂停函数执行，等待下一次召唤
        yield get_data, get_label # 有存档点的return

# 根据 x w b 计算y
def fun(x, w, b):
    pred_y = torch.matmul(x,w)+b
    return pred_y  # 返回预测的 y

# 求平均的loss
def meaLoss(pre_y, y):
    return torch.sum(abs(pre_y - y))/len(y)

# 梯度下降操作 更新参数
# 这里的para就是列表[w,b]
# 根据计算出的梯度，更新模型的参数
def sgd(paras, lr):
    with torch.no_grad(): # 告诉PyTorch：接下来的计算不要记录进"计算图"，省内存
        for para in paras: # 遍历列表，先取出 w，再取出 b
            # 3. 核心更新公式：新参数 = 旧参数 - 学习率 * 梯度
            para -= para.grad * lr

            # 4. 梯度清零
            # 类似于 C++: p->grad->reset();
            # 如果不清零，下一轮计算的梯度会累加在旧梯度上，导致方向全错
            para.grad.zero_()  #使用过的梯度，归0



# --- 第三部分：主程序执行逻辑 ---
# 1. 定义真实的规律 (上帝视角)
num = 500
true_w = torch.tensor([8.1, 2, 2, 4])
true_b = 1.1

# 2. 创造数据 (X 和 Y 都在这里生成好了)
X, Y = creat_data(true_w, true_b, num)

# 3. 模拟训练过程
batch_size = 16  # 我们决定每次给模型看 16 条数据
print("开始读取数据...\n")
# data_provider 返回的是一个生成器，我们可以直接用 for 循环遍历它
# for batch_x, batch_y in data_provider(X, Y, batch_size):
#     # 这里就是未来你写"模型训练"和"梯度下降"的地方
#     print(f"取出一批数据：X的形状 {batch_x.shape}, Y的形状 {batch_y.shape}")
#
#     # 打印其中一个具体的数值看看
#     # print(batch_x[0], batch_y[0])
print("\n数据读取完毕！")

# 4. 画个图看看（依然画第0列）
plt.scatter(X[:, 0], Y, 1)
plt.show()

# 开始训练
lr = 0.01 # 学习率
w_0 = torch.normal(0, 0.001, true_w.shape, requires_grad=True)
b_0 = torch.tensor(0.01, requires_grad=True) # b的初始值为0.01
print(w_0, b_0)

epochs = 50  # 要训练的轮数

for epoch in range(epochs):
    data_loss = 0
    for batch_x, batch_y in data_provider(X, Y, batch_size):
        pred_y = fun(batch_x, w_0, b_0)
        loss = meaLoss(pred_y, batch_y)
        loss.backward()
        sgd([w_0, b_0], lr)
        data_loss += loss # 计算loss综合

    print("epoch : %03d: loss:%.6f"%(epoch, data_loss))

print(f"真实的w值是{true_w}, 真实的b值是{true_b}")
print(f"深度训练得到的w值是{w_0} 深度训练得到的b 值是{b_0}")

# 我们通常无法在二维平面上画出所有特征。这行代码表示我们只想观察数据的第 0 个特征（即第一列数据）与结果之间的关系。
idx = 0

# 功能：画出一条直线，代表模型"认为"的数据规律。核心逻辑：它执行了线性方程公式 y = wx + b。
# X 轴数据：X[:,idx]，取输入数据 X 的第 idx 列。Y 轴数据：X[:,idx] * w_0[idx] + b_0，即 输入权重 + 偏置。这是模型计算出的预测值。
# 技术细节 (.detach().numpy())：因为 X, w_0, b_0 都是 PyTorch 的 Tensor（张量），包含梯度信息（Gradient），matplotlib 无法直接处理。.detach()：从计算图中分离，不再追踪梯度。.numpy()：将 Tensor 转换为 Python 的 NumPy 数组，以便画图库能够读取。
plt.plot(X[:,idx].detach().numpy(),X[:,idx].detach().numpy()*w_0[idx].detach().numpy()+b_0.detach().numpy())
plt.scatter(X[:,idx], Y, 1)
plt.show()
相关推荐
cskywit1 小时前
[Nature 2026]AFLoc：一种用于通用无标注病理局部定位的多模态视觉‑语言模型
人工智能·深度学习·语言模型
victory04311 小时前
pytorch函数使用规律-不必再死记硬背
人工智能·pytorch·python
rjc_lihui1 小时前
LightGBM 从入门到精通 (来自deepseek)
python
YUISOK2 小时前
如何使用uiautomator2+Weditor 可视化查看一个app组件的vm树
python·软件工程
Hcoco_me2 小时前
大模型面试题88：cuda core的数量 与 开发算子中实际使用的线程 关系是什么？过量线程会发生什么情况？
人工智能·深度学习·机器学习·chatgpt·职场和发展·机器人
Pyeako2 小时前
opencv计算机视觉--图形旋转&图形可视化&均衡化
人工智能·python·opencv·计算机视觉·图形旋转·图形可视化·均衡化
菜宾2 小时前
java-分布式面试题（事务+锁+消息队列+zookeeper+dubbo+nginx+es）
java·开发语言·分布式
人工智能AI技术2 小时前
【Agent从入门到实践】28 开发第一个Agent——开发准备：环境搭建（Python、依赖库、大模型API密钥）
人工智能·python
Remember_9932 小时前
【LeetCode精选算法】位运算专题一
java·开发语言·数据结构·leetcode·哈希算法
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)03Claude Code Skills 实用使用手册04UV安装并设置国内源05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06BongoCat - 跨平台键盘猫动画工具07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南09Linux下V2Ray安装配置指南10Open Code教程（四）| 高级配置与集成