（本博客为Datawhale的baseLLM开源学习项目的学习笔记）
在之前的内容中，我们探讨了以Adapter和各类Prompt Tuning为代表的PEFT技术。它们通过在模型中插入新的模块或在输入端添加可学习的提示，巧妙地实现了高效微调。这些方法地核心，都是在尽量不"打扰"原始模型权重的前提下，通过影响模型的激活值来适应新任务。
接下来，我们将介绍另一种方法，也是当前社区应用最广泛的PEFT方法--LoRA（Low-Rank Adaptation of Large Language Models）。它不再"绕道而行"，而是直击模型的权重矩阵，并提出一个观点。那就是大模型的参数更新，或许并不需要那么"兴师动众"。
一、低秩近似的核心思想
全量微调之所以成本高昂，是因为它需要为模型中每一个权重矩阵W（维度可能高达数万）计算并存储一个同样大小的更新矩阵△W。为了解决这个问题，研究者们提出了像Adapter Tuning和Prompt Tuning这样的参数高效微调方法。但是，它们也存在一一些为解决的痛点。Adapter虽好，却会引入额外的推理延迟；Prompt Tuning则会占用输入序列长度，且优化难度较高。
因此我们会提出一个问题，有没有一种方法，既可以大幅减少参数，又不引入推理延迟，还能直接作用于模型权重呢？这就是LoRA试图回答的问题。它的提出源于一个假设：
大语言模型是过参数化的（Over-parametrized），它们在针对特定任务进行微调时，权重更新矩阵△W具有一个很低的"内在秩"（Intrinsic Rank）。
这意味着，尽管△W的维度很高，但它所包含的"有效信息"实际上可以被一个远小于其规模的低秩矩阵来表示。对此，LoRA的核心思想就是用两个更小的"低秩"矩阵A和B的乘积，来模拟这个庞大的更新矩阵△W。
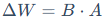
其中，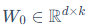
，低秩分解后的
，
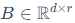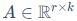，而秩
。
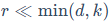LoRA的工作方式可以理解为在原始的预训练权重W0旁边，增加了一个并行的"旁路"结构，如下图所示计算分为两条路径：
1.**主路：**输入x经过原始的、被冻结的预训练权重W0。
2.**旁路：**输入x依次通过两个低秩矩阵A和B。矩阵A先将输入维度从k"压缩"到一个很小的秩r，然后再由矩阵B"解压"回输出维度d。
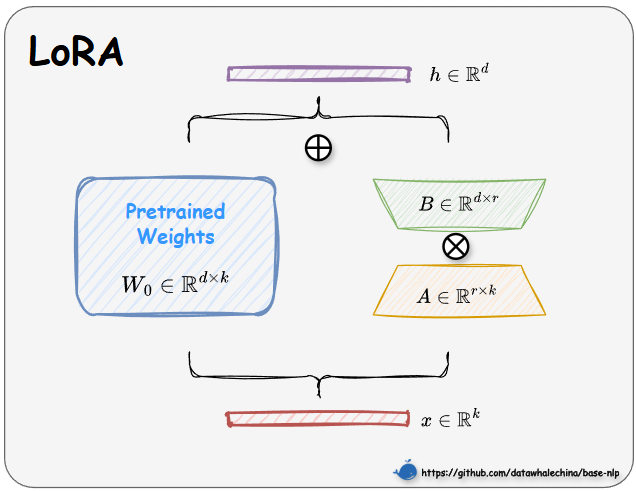
最终的输出h是这两条路径结果的加和：
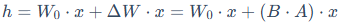
在训练时，只有旁路的矩阵A和B会被更新。通过这种方式，需要优化的参数量就从d x k下降到了d x r + r x k。通常，秩r会选择一个非常小的值（如8，16，64），使得可训练参数量仅为全量微调的千分之一甚至万分之一。
训练时主要包括两个流程：
**初始化：**如上图所示，旁路矩阵有特殊的初始化方式。矩阵A通常使用高斯分布进行随机初始化，而矩阵B则初始化为全零。这样做可以确保在训练开始时，旁路输出为零，微调是从原始的预训练模型状态开始的，保证了训练初期的稳定性。
缩放： LoRA的前向计算公式会包含一个缩放因子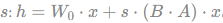
。这个s通常设为α/r，其中α是一个可调超参。这个缩放操作有助于在调整秩r时，减少对学习率等其他超参数的重新调整需求，让训练过程更稳定。
二、LoRA的优势与实践
相比于之前介绍的PEFT方法，LoRA以其独特的结构带来了显著的优势，下面来具体看一下。
1.核心优势
LoRA凭借其独特的并行结构和直接作用于权重的特性，展现出几大核心优势：
**更高的参数与存储效率：**对于每一个下游任务，不再需要存储一个完整的模型副本，而只需保存极小的矩阵A和B。论文指出，这可以将模型checkpoints的体积缩小高达10000倍（例如从350GB减少到35MB）。在训练时，由于无需为冻结的参数计算梯度和存储优化器状态，可以节省高达2/3的GPU显存，并提升约25%的训练速度。
**零额外推理延迟：**这是LoRA相比Adapter Tuning最具吸引力的优点。Adapter在模型中串行地引入了新的计算层，不可避免地会增加推理延迟。而LoRA地旁路结构在训练完成后，可以通过矩阵加法（W' = W0 + s*B*A）直接"合并"回原始权重中。这样，模型的网络结构与原始模型完全一致，不会引入任何额外的计算步骤。
**效果媲美全量微调，且不占用输入长度：**与Prompt-Tuning等作用于输入激活值的方法不同，LoRA直接修改权重矩阵，能更深入、更直接地影响模型的行为，效果也更接近于全量微调。同时，它不添加任何virtual token，不会占用上下文长度，在处理长文本任务时更有优势。
**良好的可组合性：**LoRA的设计是正交的，它可以与Prefix-Tuning等其他PEFT方法结合使用，取长补短，进一步提升模型性能。
2.关键实践
LoRA虽然强大，但也带来了新的超参数选择问题：应该对哪些权重矩阵应用LoRA？秩r又该如何选择？幸运的是，原始论文通过大量实验为我们提供了指导。
首先是第一个问题：应该对哪些权重矩阵应用LoRA？
LoRA的作者为了简化问题和提高参数效率，将研究范围限定在了自注意力模块（Self-Attention）的权重矩阵上，并冻结了前馈神经网络等其他模块。在自注意力模块中，主要有四个权重矩阵：
查询（Query）的Wq、键（Key）的Wk、值（Value）的Wv和输出（Output）的W0。通过原文的实验数据（如下表所示）可以发现一个规律。在固定的可训练参数预算下，将LoRA应用于多种类型的注意力权重（特别是Wq和Wv的组合）通常比把所有预算用于增大单一类型权重的秩（rank）效果更好。所以，原论文提出并验证了一个高效的策略：仅在注意力模块中应用LoRA，并冻结模型的其余部分。
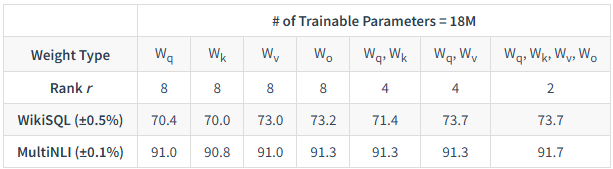
第二个问题：秩r又该如何选择？
通过下表的实验结果可以看到，一个非常小的秩r（例如4，8甚至1）就已经足够强大。盲目增大r不仅会增加参数量，有时甚至会导致性能下降。例如，对于Wq和Wv的组合，即使秩r仅为1或2，模型在各项任务上的表现也已具竞争力，甚至超过了r = 64的情况。这说明权重更新确实是低秩的。
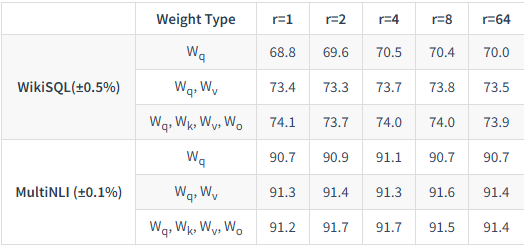
最后一个问题是：LoRA究竟是如何生效的？
论文通过分析发现，它学习到的更新矩阵△W并不是对原始权重W0中最重要特征的简单复制，恰恰相反，它学习到的那些在预训练中学习到但未被充分强调、却对下游任务至关重要的"隐藏特征"，并对其进行大幅放大。它不是在重复模型已经很擅长的事情，而是在"查漏补缺"，精准地增强了模型在特定任务上所欠缺的能力。
三、AdaLoRA自适应微调
尽管我们根据上述实验知道了应该优先微调注意力权重、并选择一个较小的秩r，但LoRA这种固定的设置方式仍然引入了新的问题：
**秩r的选择：**r应该设为多大？这是一个固定的超参数，无法在训练中自适应调整。
**微调目标的选择：**应该对哪些权重矩阵（Wq，Wk，Wv，W0还是前馈网络的矩阵）应用LoRA？原始LoRA论文的实验主要集中在注意力模块，忽略了FFN模块，但后续研究发现FFN的微调同样重要。
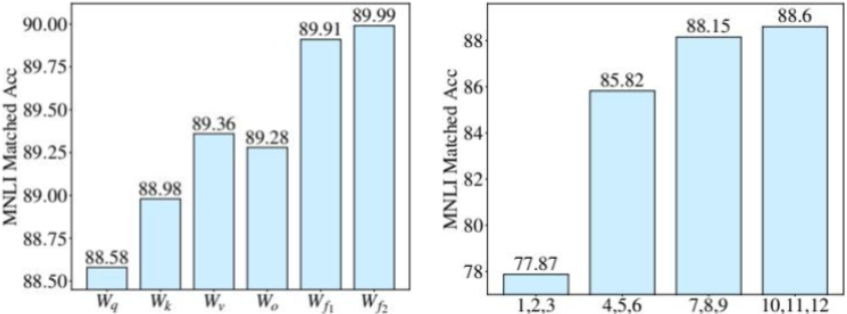
实验表明，为所有矩阵和所有层级设置一个统一的、固定的秩r，远非最优解。不同任务、不同模型层、不同权重矩阵，其"可塑性"和对任务的重要性是不同的，它们理应被区别对待。手动为每个矩阵和层级寻找最优秩的组合，其超参数空间巨大，几乎不可能完成。不过，如下图实验所示，已经揭示了这种重要性的差异：
左侧显示，在固定的参数预算下，微调前馈网络（FFN）模块的权重带来的性能收益，显著高于微调注意力模块的权重。
右侧则表明，微调模型更高层级（如10-12层）的权重，也比微调底层（如1-3层）能带来更大的性能提升。
为了解决固定秩分配的次优性与手动调参的困难，AdaLoRA（Adaptive LoRA）提出了一种更智能的、自适应的LoRA方案-根据权重的重要性，动态地、有选择地为不同模块分配参数预算。AdaLoRA不再使用固定的秩r，而是让模型在训练过程中自己"决定"哪些部分更需要被微调，以及需要多大的"力度"（秩）去微调。这一过程主要包含三个关键创新。
1.基于SVD的参数化
AdaLoRA的第一步，是对LoRA的低秩分解形式进行了改进。它不再是使用两个简单的矩阵B·A，而是引入了经典的**奇异值分解（SVD）**思想来参数化更新矩阵△W：
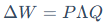
在机器学习和信号处理中，SVD是一种强大的矩阵分解技术，能将任意矩阵分解为三个矩阵的乘积：一个左奇异向量矩阵P、一个对角矩阵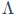
和一个右奇异向量矩阵Q。其中，对角线上的奇异值代表了数据中最重要的主成分。AdaLoRA正是借鉴了这一思想。
这种参数化方式有两大好处：
1.避免了高昂的计算成本： 他只是在形式上模拟了SVD，在训练时P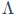，，Q都是可训练的参数，并不需要对△W进行真正的、计算开销极大的SVD分解。
2.结构化的重要性： 这种分解△W的更新信息解耦为三个部分：P和Q决定了更新的"方向"，而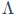中的奇异值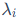
则决定了在对应方向上的更新"幅度"。这使得我们可以通过调整奇异值的大小来直接控制每个"更新分量"的重要性，也即调整矩阵的秩。
为确保P和Q在训练中保持正交性（这是奇异向量的性质），AdaLoRA还在训练损失中加入了一个正交正则化项，以保证分解的稳定性和有效性。
2.重要性评分与动态预算分配
有了SVD这种分解结构，AdaLoRA接下来要解决的问题就是如何衡量每个"更新分量"的重要性？
它将每个奇异值和其对应的左右奇异向量组合成一个"三元组"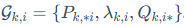
。在训练过程中，AdaLoRA会为每个三元组计算一个重要性分数
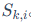。这个分数是基于对三元组中每个参数ω的重要性s(ω)进行聚合得到的。
参数ω的重要性s(ω)由两部分相乘得到，分别是平滑后的参数敏感度（Sensitivity）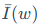
和不确定性（Uncertainty）
。
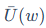**参数敏感度（Sensitivity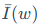）：**它被定义为参数自身大小与其梯度的乘积的绝对值，即。其直观含义是：如果将这个参数ω置零，模型损失会发生多大的变化。敏感度越高，说明该参数对当前任务的性能影响越大。
**不确定性（Uncertainty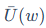）：**由于训练是分批次（mini-batch）进行的，单个批次计算出的梯度具有随机性，导致敏感度I的值会剧烈波动。为了得到更稳定的评估，AdaLoRA引入了指数移动平均（EMA）来对敏感度和不确定性进行平滑处理：
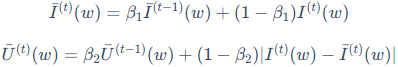
其中，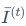
是平滑后的敏感度，而
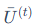则量化了瞬时敏感度与平滑后值得偏差，即"不确定性"。一个参数如果不仅敏感度高，而且这种敏感性在训练中持续稳定出现（即不确定性低），那么它就更重要。
最终，单个三元组的重要性分数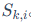由其内部所有参数的重要性聚合而成：
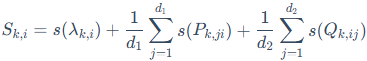
其中d1 = d，d2 = k（对应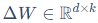
）。
在计算出所有三元组的重要性分数后，AdaLoRA会进行排序，并根据一个预设的参数预算（总秩），裁剪掉那些得分最低的三元组（即将它们对应的奇异值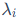置为0），从而实现了参数的动态分配。
3.全局预算调度器与目标函数
为了让训练过程更加稳定和高效，AdaLoRA的整体目标函数L包含了原始的损失函数C和我们前面提到的正交正则项R：
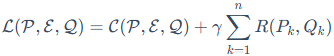
同时，它还引入了全局预算调度器（Global Budget Scheduler）的策略。这里的"预算"b(t)，指的就是在训练的第t步，模型总共保留的奇异值的数量。它由一个分段函数精确控制：
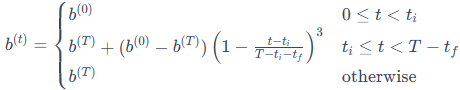
这个调度策略包含三个阶段：
1.**热身阶段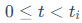
：**从一个比目标预算b(T)略高的初始预算b(0)开始训练，让模型有更充分的机会去"探索"所有参数的潜在重要性。
2.**裁剪阶段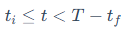
：**按照一个三次方的调度曲线，逐步地裁剪掉重要性分数较低的奇异值，将预算平滑地降低到最终的目标值。
3.**微调阶段：**在预算分配基本稳定后，固定预算b(T)（即锁定了最重要的参数），继续对模型进行微调直至收敛。
这种"先探索、后收敛"的策略，让模型有更充分的机会去发现哪些权重真正重要，从而做出更优的预算分配决策。最终，AdaLoRA实现了在训练过程中对秩的动态调整和在不同模块间的智能分配。
在下图中可以看出，模型自动为FFN模块（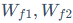
）以及模型的高层（层级6-12）分配了更高的秩（颜色更深），这与上述的实验结果吻合，证明了自适应机制的有效性。
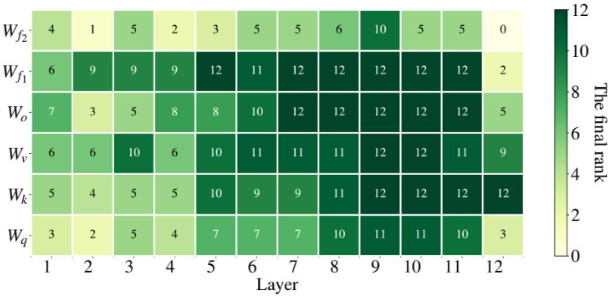
论文的实验结果也表明，AdaLoRA的自适应机制是有效的。它能自动发现前馈网络和模型顶层的权重矩阵更为重要，并为其分配更高的秩。此外，消融实验证明，即使不使用动态预算分配，仅仅将参数化形式从B·A替换为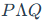
，就已经能带来性能提升，说明SVD结构本身的优越性。
这种自适应的机制，让AdaLoRA在相同的参数预算下，往往能达到比原始LoRA更好的性能，进一步提升了参数高效微调的水平。
四、QLoRA参数压缩
LoRA和AdaLoRA分别从"低秩近似"和"自适应秩分配"两个角度优化了微调过程，但它们都还有一个共同的前提，原始的、被冻结的大模型权重仍然是以较高的精度（如FP16或BF16）加载到显存中的。对于动辄几百上千亿参数的模型来说，这部分权重本身就是一笔巨大的显存开销。
华盛顿大学的研究者们提出了QLoRA（Quantized LoRA），一种更高阶的参数高效微调方法。它通过一系列压缩技术，实现了很不错的效果。在保持与16-bit全量微调相当性能的同时，成功将一个65B（650亿）参数模型的微调任务，压缩到了一块48GB显存的GPU上。如下图所示，与冻结16-bit模型的标准LoRA相比，QLoRA更进一步，将基座模型量化为4-bit。训练时，梯度会穿过被冻结的4-bit模型，反向传播到16-bit的适配器中，并只更新适配器参数。此外，它还引入了分页优化器，在显存不足时，可以将优化器状态临时卸载到CPU内存，从而有效管理内存峰值。
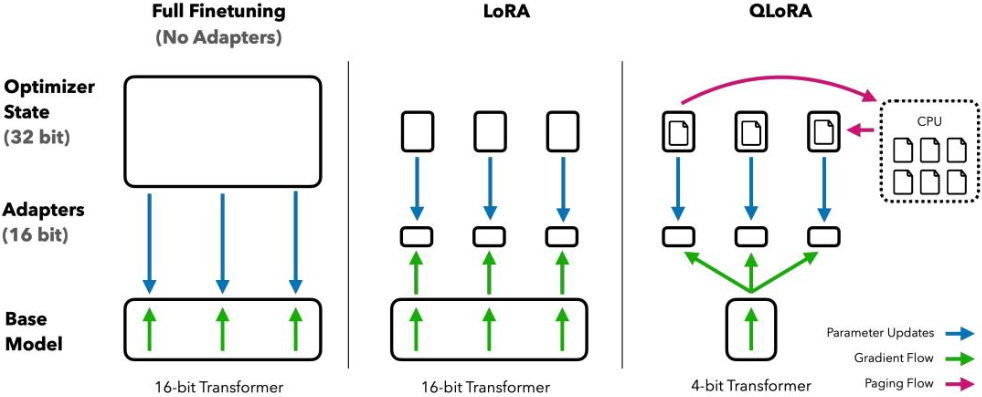
基于这些创新，QLoRA训练出的Guanaco模型系列，在Vicuna基准测试中甚至达到了ChatGPT 99.3%的性能水平，而这仅仅需要单张GPU训练24小时。QLoRA的成功，主要归功于三方面的创新：4-bit NormalFloat（NF4） 、双量化（Double Quantization） 和分页优化器。
1.4-bit NormalFloat数据类型
量化是模型压缩领域的常用技术，通过用更少的信息位数（bit）来表示数值，从而减少模型体积和显存占用。然而，传统的量化方法（如均匀量化）在面对神经网络权重时会遇到一个难题：权重值的分布通常是零中心的正态分布，其中大部分值集中在0附近，而少量"离群值"的绝对值又非常大。均匀的量化策略无法很好地适应这种非均匀分布，导致较大的精度损失。
以一个典型的8-bit均匀量化为例，其量化过程由以下公式定义：
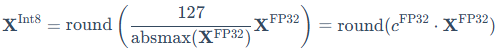
这个过程依赖于absmax缩放，即找到张量中的绝对值最大值来计算缩放系数，也就是量化常数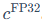
。这种方法对离群值非常敏感，也是它的主要局限性。反量化则是其逆过程：
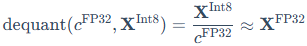
理解这个基础过程，特别是"量化常数"的概念，对于我们后续理解QLoRA的双量化会有所帮助。
那么，为了解决传统量化方法的问题，QLoRA提出了一种专门为正态分布权重设计的4-bit数据类型-NormalFloat（NF4）。它被证明是一种信息论上最优的数据类型，其设计哲学基于"分位数量化（Quantile Quantization）"。
分位数量化旨在让每个量化"桶"中，都包含相同数量的来自目标分布的值。这意味着，在数据密集的区域（如正态分布的中心），量化点会更密集；在数据稀疏的区域（如分布的两尾），量化点会更稀疏。NF4的具体构建步骤如下：
**1.确定理论分布：**首先，构建一个理论上的标准正态分布N(0, 1)。
2.计算分位数： 为这个标准正态分布精确计算出
个值，这些值能将该分布的累积密度函数（CDF）划分为16个等概率的区间。这些计算出的分位数点，就构成了NF4数据类型能够表示的所有数值。
**3.归一化与量化：**在对实际的模型权重（通常以block为单位处理）进行量化时，首先通过"绝对值最大缩放"（absmax rescaling）进行归一化。具体来说，就是找到当前权重块中的绝对值最大值，并计算出其缩放因子，这个因子就是该块的量化常数，它通常是一个32-bit浮点数。将块内所有权重都乘以这个缩放因子，就可以将它们的数值范围归一化到[-1，1]区间。最后，将每一个归一化后的权重值，映射到离它最近的NF4分位数点上。
更精确地说，一个k-bit的NormalFloat数据类型（NFk）包含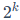
个量化点（qi），其数值是通过以下公式估算的：
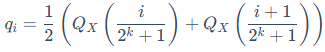
这里的Qx()是标准正态分布N(0, 1)的分位数函数（Quantile Function）。该函数的作用是，给定一个概率值p（在0到1之间），它能返回在该概率点上的具体数值。公式中的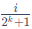
和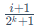
就是将累积概率分布划分为
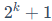个等份的点。整个公式的含义是，第i个量化点qi的值，被定义为标准正态分布中第i个和第i + 1个等概率区间隔断点的中点。
通过这种方式，NF4用极其有限的4个bit，实现了对正态分布数据的高精度近似，最大程度地保留了原始权重中的信息，远优于传统的4-bit整数或浮点数量化。
2.双量化与分页优化器
除了开创性的NF4数据类型，QLoRA还引入了另外两项技术来进一步压缩显存。
**双量化（Double Quantization，DQ）：**上述量化过程需要为每一组（block）权重存储一个对应的"量化常数"（通常是32-bit的浮点数）。对于一个巨大的模型，这些量化常数累加起来也会占用相当大的显存。例如，对于一个block size为64的权重块，这些常数平均会给每个参数带来32/64=0.5bit的额外开销。双量化的思想是，对这些量化常数本身，再进行一次量化。通过用8-bit浮点数对第一级量化常数进行第二级量化，可以将这部分额外开销从每参数0.5bit大幅降低到约0.127bit。
分页优化器（Paged Optimizers）：在微调过程中，梯度和优化器状态（如Adam算法中的动量和方差）会产生瞬时的显存峰值，尤其是在处理长序列时，很容易导致显存溢出（OOM）。分页优化器借鉴了操作系统中"虚拟内存"的思想，它利用NVIDIA统一内存（Unified Memory）的特性，在GPU显存不足时，能自动地、按需地将一部分优化器状态"分页"暂存到CPU内存中，待需要时再加载回GPU。这极大地提高了训练过程的稳定性，避免了因偶然的显存峰值而导致的训练失败。
3.QLoRA的工作流程
结合上述技术，QLoRA的完整微调流程可以概括为一种"存算分离"的巧妙设计：它使用一种低精度的数据类型进行存储，但在计算时又恢复为高精度。整个流程可以分为以下几个步骤：
1.**加载与量化（存）：**加载16-bit的预训练模型，然后将其权重量化为4-bit的NF4格式，并应用双量化进一步压缩量化常数。此时，巨大的基座模型以极低的显存占用被冻结在GPU中。
2.**前向传播（算）：**在模型中插入LoRA适配器，其权重保持为16-bit精度（BF16）.当进行前向计算时，需要使用的基座模型权重会被动态地反量化回16-bit的BF16格式。计算完成后，这些临时的16-bit权重立即被丢弃，显存得以释放。
3.**反向传播与更新：**在反向传播过程中，梯度只会通过冻结的4-bit模型反向传播到16-bit的LoRA适配器中，并只更新适配器的权重。如果出现显存峰值，分页优化器会介入，防止OOM发生。
这个"存算分离"的前向传播过程，可以用以下公式进行精确地数学描述：
第一部分（主路）： doubleDequant函数对应了步骤2中的核心操作，它将4-bit的权重
动态恢复为16-bit，再与16-bit的输入
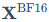相乘。
第二部分（旁路）：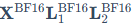 
则是标准的LoRA模块，其计算全程保持16-bit精度。