二阶与三阶行列式
一、二阶行列式
1、定义
由两行两列数字构成的方阵:
∣ a 11 a 12 a 21 a 22 ∣ \left| \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right| a11a21a12a22
称为二阶行列式 ,记作 d e t ( A ) 或 ∣ A ∣ det (A)或|A| det(A)或∣A∣,其值为:
D = a 11 a 22 − a 12 a 21 D = a_{11}a_{22} - a_{12}a_{21} D=a11a22−a12a21
a 11 、 a 22 a_{11}、a_{22} a11、a22等数据被称为元素。
计算规律:对角线法则
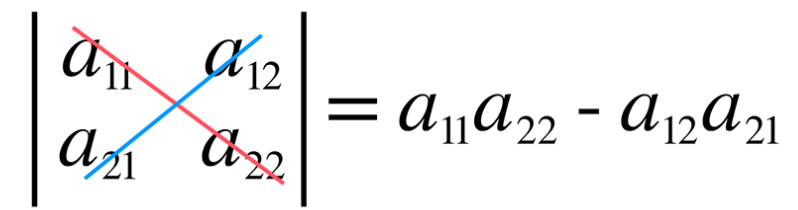
红色称为主对角线,蓝色称为副对角线,主对角线上的元素乘积减去副对角线上的元素乘积即可。
2、几何意义
在平面直角坐标系中,若以向量 α ⃗ 1 = ( a 11 , a 21 ) T \vec{\alpha}1 = (a{11}, a_{21})^{\text{T}} α 1=(a11,a21)T 和 α ⃗ 2 = ( a 12 , a 22 ) T \vec{\alpha}2 = (a{12}, a_{22})^{\text{T}} α 2=(a12,a22)T 为邻边的平行四边形面积为 S S S,则 ∣ D ∣ = S |D| = S ∣D∣=S,符号表示方向(右手系为正)。
二、三阶行列式
1、定义
由三行三列数字构成的方阵:
∣ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ \left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| a11a21a31a12a22a32a13a23a33
称为三阶行列式 ,其值为:
D = a 11 a 22 a 33 + a 12 a 23 a 31 + a 13 a 21 a 32 − a 13 a 22 a 31 − a 11 a 23 a 32 − a 12 a 21 a 33 \begin{aligned} D &= a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ &\quad - a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{aligned} D=a11a22a33+a12a23a31+a13a21a32−a13a22a31−a11a23a32−a12a21a33
计算规律:对角线法则
先将三阶行列式的前两列元素加在三阶行列的右边,作为辅助列,然后,
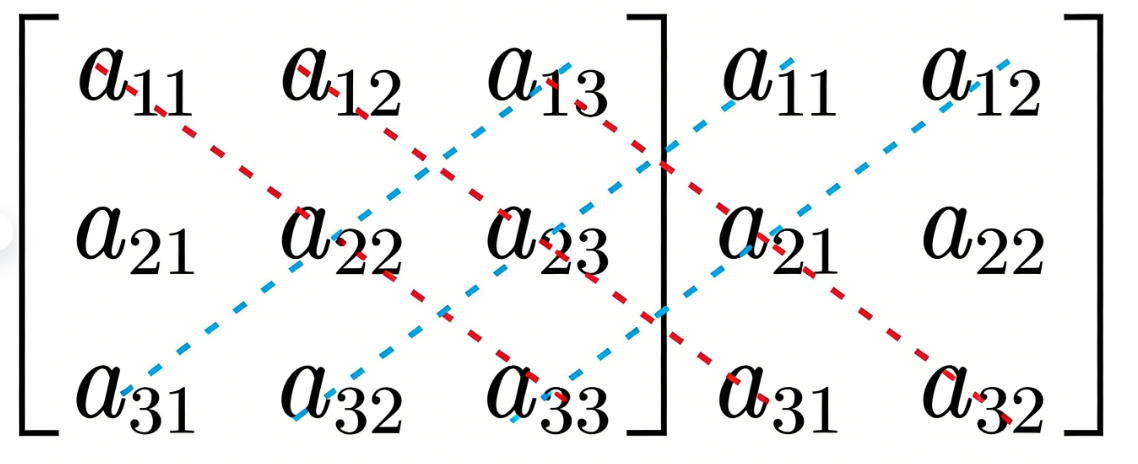
三条红色对角线上的元素相乘再相加的和,减去三条蓝色对角线上的元素相乘
2、几何意义
在三维空间中,若以向量 α ⃗ 1 = ( a 11 , a 21 , a 31 ) T \vec{\alpha}1 = (a{11}, a_{21}, a_{31})^{\text{T}} α 1=(a11,a21,a31)T, α ⃗ 2 = ( a 12 , a 22 , a 32 ) T \vec{\alpha}2 = (a{12}, a_{22}, a_{32})^{\text{T}} α 2=(a12,a22,a32)T, α ⃗ 3 = ( a 13 , a 23 , a 33 ) T \vec{\alpha}3 = (a{13}, a_{23}, a_{33})^{\text{T}} α 3=(a13,a23,a33)T 为棱的平行六面体体积为 V V V,则 ∣ D ∣ = V |D| = V ∣D∣=V。
三、行列式的计算(二、三阶)
例1: 计算
D = ∣ 2 1 − 1 3 ∣ D = \left| \begin{array}{cc} 2 & 1 \\ -1 & 3 \end{array} \right| D= 2−113
解:
D = 2 × 3 − 1 × ( − 1 ) = 6 + 1 = 7 D = 2 \times 3 - 1 \times (-1) = 6 + 1 = 7 D=2×3−1×(−1)=6+1=7
例2: 计算
D = ∣ 1 2 3 0 4 5 1 0 6 ∣ D = \left| \begin{array}{ccc} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 1 & 0 & 6 \end{array} \right| D= 101240356
解:
D = 1 × 4 × 6 + 2 × 5 × 1 + 3 × 0 × 0 − 3 × 4 × 1 − 1 × 5 × 0 − 2 × 0 × 6 = 24 + 10 + 0 − 12 − 0 − 0 = 22. \begin{aligned} D &= 1 \times 4 \times 6 + 2 \times 5 \times 1 + 3 \times 0 \times 0 \\ &\quad - 3 \times 4 \times 1 - 1 \times 5 \times 0 - 2 \times 0 \times 6 \\ &= 24 + 10 + 0 - 12 - 0 - 0 = 22. \end{aligned} D=1×4×6+2×5×1+3×0×0−3×4×1−1×5×0−2×0×6=24+10+0−12−0−0=22.
四、应用案例
案例1 求平面三角形面积
若已知三角形顶点坐标 P 1 ( x 1 , y 1 ) P_1(x_1, y_1) P1(x1,y1), P 2 ( x 2 , y 2 ) P_2(x_2, y_2) P2(x2,y2), P 3 ( x 3 , y 3 ) P_3(x_3, y_3) P3(x3,y3),则面积
S = 1 2 ∣ x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 ∣ S = \frac{1}{2} \left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right| S=21 x1x2x3y1y2y3111
例如,求 P 1 ( 0 , 0 ) P_1(0,0) P1(0,0), P 2 ( 2 , 1 ) P_2(2,1) P2(2,1), P 3 ( 1 , 3 ) P_3(1,3) P3(1,3) 所围三角形面积。
解:
S = 1 2 ∣ 0 0 1 2 1 1 1 3 1 ∣ = 1 2 ( 0 + 0 + 1 ⋅ ( 2 ⋅ 3 − 1 ⋅ 1 ) − 0 − 0 − 0 ) = 1 2 × ( 6 − 1 ) = 2.5. S = \frac{1}{2} \left| \begin{array}{ccc} 0 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 3 & 1 \end{array} \right| = \frac{1}{2} \big( 0+0+1\cdot(2\cdot 3 - 1\cdot 1) - 0 - 0 - 0 \big) = \frac{1}{2} \times (6-1) = 2.5. S=21 021013111 =21(0+0+1⋅(2⋅3−1⋅1)−0−0−0)=21×(6−1)=2.5.
案例2 地图APP中的线性变换
场景:
小明使用地图APP查看家附近的公园。APP提供地图的缩放、旋转功能,这些操作在数学上就是线性变换,可以用矩阵表示,而行列式则告诉小明地图显示的面积变化了多少倍。
具体内容:
假设公园在原始地图上是一个矩形区域,由两个边向量表示:
v ⃗ 1 = ( 1 , 0 ) (东边1公里) , v ⃗ 2 = ( 0 , 0.5 ) (北边0.5公里) \vec{v}_1 = (1, 0) \quad \text{(东边1公里)},\quad \vec{v}_2 = (0, 0.5) \quad \text{(北边0.5公里)} v 1=(1,0)(东边1公里),v 2=(0,0.5)(北边0.5公里)
原始面积 = 1 × 0.5 = 0.5 1 \times 0.5 = 0.5 1×0.5=0.5 平方公里。
小明进行了两个操作:
- 旋转地图:逆时针旋转30°(保持形状不变)
- 缩放地图:横向拉伸1.2倍,纵向拉伸1.5倍
组合操作用一个变换矩阵表示(旋转+缩放):
T = ( 1.2 cos 30 ∘ − 1.5 sin 30 ∘ 1.2 sin 30 ∘ 1.5 cos 30 ∘ ) ≈ ( 1.039 − 0.75 0.6 1.299 ) T = \begin{pmatrix} 1.2\cos 30^\circ & -1.5\sin 30^\circ \\ 1.2\sin 30^\circ & 1.5\cos 30^\circ \end{pmatrix} \approx \begin{pmatrix} 1.039 & -0.75 \\ 0.6 & 1.299 \end{pmatrix} T=(1.2cos30∘1.2sin30∘−1.5sin30∘1.5cos30∘)≈(1.0390.6−0.751.299)
计算变换后的面积变化率(行列式):
det ( T ) = ( 1.039 × 1.299 ) − ( − 0.75 × 0.6 ) = 1.349 + 0.45 = 1.799 \det(T) = (1.039 \times 1.299) - (-0.75 \times 0.6) = 1.349 + 0.45 = 1.799 det(T)=(1.039×1.299)−(−0.75×0.6)=1.349+0.45=1.799
实际意义:
- 面积变化:公园在屏幕上的显示面积变为原来的1.799倍。如果原始面积0.5 km²,现在显示面积约0.8995 km²。
- 导航准确性:如果APP要计算公园内的步行路径长度,需要知道这个缩放比例来校正距离。
- 数据加载:当地图放大时(行列式>1),APP需要加载更精细的地图数据;缩小时(行列式<1),可以加载粗略数据以节省流量。
更贴近生活的理解:
想象你在手机屏幕上用两根手指做"放大缩小旋转"手势时:
- 行列式 > 1:你正在放大地图,看到的细节更多,但显示范围变小
- 行列式 = 1:你只是旋转地图,显示的面积大小不变
- 行列式 = 0:错误情况(地图被"压扁"成一条线,APP会崩溃或显示错误)
- 行列式 < 0:做了镜像翻转(比如从看地图正面变成看反面)
数学到生活的桥梁:
det ( T ) = 1.799 ⇒ "你现在看到的地图区域,实际面积是屏幕测量的1.799倍" \det(T) = 1.799 \quad \Rightarrow \quad \text{"你现在看到的地图区域,实际面积是屏幕测量的1.799倍"} det(T)=1.799⇒"你现在看到的地图区域,实际面积是屏幕测量的1.799倍"
这个值帮助APP:
- 准确计算实时距离
- 优化地图瓦片加载
- 保持比例尺正确显示
- 在AR导航中正确叠加虚拟信息到真实场景
五、总结
- 二阶行列式: a 11 a 22 − a 12 a 21 a_{11}a_{22} - a_{12}a_{21} a11a22−a12a21,对应平行四边形有向面积。
- 三阶行列式:对角线法则(六项代数和),对应平行六面体有向体积。
- 对角线法则只能用于二阶和三阶行列式。
- 应用:几何面积/体积计算、三角形面积公式等。